15.4: Одновимірні зіткнення між двома об'єктами

Одновимірне пружне зіткнення в лабораторному опорному кадрі

Розглянемо одновимірне пружне зіткнення двох об'єктів, що рухаються в х - напрямку. Один об'єкт, з масою\(m_{1}\) і початковою x -складовою швидкості\(\mathcal{V}_{1 x, i}\) стикається з об'єктом маси\(m_{2}\) і початковою x -складовою швидкості\(\mathcal{V}_{2 x, i}\). Скалярні складові\(v_{1 x, i}\) і\(v_{1 x, i}\) можуть бути додатними, негативними або нульовими. Ніякі сили, крім сили взаємодії між об'єктами, не діють під час зіткнення. Після зіткнення кінцевою x -складовою швидкостей є\(v_{1 x, f}\) і\(v_{2 x, f}\). Ми називаємо цю опорну рамку «лабораторним еталонним фреймом».

Малюнок 15.5 Одновимірне пружне зіткнення, лабораторний опорний каркас

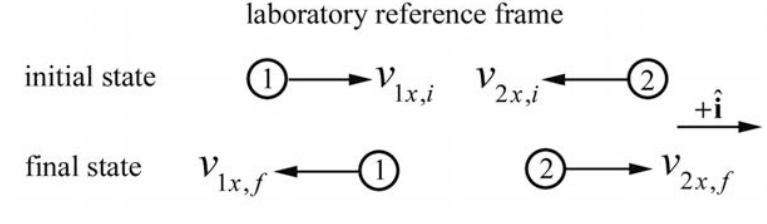
За зіткнення зображено на малюнку 15.5\(v_{1 x, i}>0, \quad v_{2 x, i}<0, \quad v_{1 x, f}<0\), і\(v_{2 x, f}>0\). Оскільки в х -напрямку немає зовнішніх сил, імпульс постійний в х - напрямку. Прирівнювання компонентів імпульсу до і після зіткнення дає відношення

\[m_{1} v_{1 x, i}+m_{2} v_{2 x, i}=m_{1} v_{1 x, f}+m_{2} v_{2 x, f} \nonumber \]

Оскільки зіткнення еластичне, кінетична енергія постійна. Прирівнювання кінетичної енергії до і після зіткнення дає відношення

\[\frac{1}{2} m_{1} v_{1 x, i}^{2}+\frac{1}{2} m_{2} v_{2 x, i}^{2}=\frac{1}{2} m_{1} v_{1 x, f}^{2}+\frac{1}{2} m_{2} v_{2 x, f}^{2} \nonumber \]

Перепишіть ці рівняння (15.3.1) та (15.3.2) як

\[m_{1}\left(v_{1 x, i}-v_{1 x, f}\right)=m_{2}\left(v_{2 x, f}-v_{2 x, i}\right) \nonumber \]

\[m_{1}\left(v_{1 x, i}^{2}-v_{1 x, f}^{2}\right)=m_{2}\left(v_{2 x, f}^{2}-v_{2 x, i}^{2}\right) \nonumber \]

Рівняння (15.3.4) можна записати як

\[m_{1}\left(v_{1 x, i}-v_{1 x, f}\right)\left(v_{1 x, i}+v_{1 x, f}\right)=m_{2}\left(v_{2 x, f}-v_{2 x, i}\right)\left(v_{2 x, f}+v_{2 x, i}\right) \nonumber \]

Розділити рівняння (15.3.4) на рівняння (15.3.3), що дає

\[v_{1 x, i}+v_{1 x, f}=v_{2 x, i}+v_{2 x, f} \nonumber \]

Рівняння (15.3.6) можна переписати як

\[v_{1 x, i}-v_{2 x, i}=v_{2 x, f}-v_{1 x, f} \nonumber \]

Нагадаємо, що відносна швидкість між двома об'єктами визначається як

\[\overrightarrow{\mathbf{v}}^{\mathrm{rel}} \equiv \overrightarrow{\mathbf{v}}_{1,2} \equiv \overrightarrow{\mathbf{v}}_{1}-\overrightarrow{\mathbf{v}}_{2} \nonumber \]

де ми використовували верхній індекс «rel», щоб нагадати собі, що швидкість - це відносна швидкість (і для спрощення наших позначень). Таким чином,\(v_{x, i}^{\mathrm{rel}}=v_{1 x, i}-v_{2 x, i}\) є початковою x -складовою відносної швидкості, і\(v_{x, f}^{\mathrm{rel}}=v_{1 x, f}-v_{2 x, f}\) є кінцевою x -складовою відносної швидкості. Тому рівняння (15.3.7) стверджує, що під час взаємодії початкова відносна швидкість дорівнює негативній кінцевої відносної швидкості.

\(\overrightarrow{\mathbf{v}}_{i}^{\mathrm{rel}}=-\overrightarrow{\mathbf{v}}_{f}^{\mathrm{rel}}\)(1− принцип мірної енергії-імпульсу).

Отже, початкова і кінцева відносні швидкості рівні. Ми назвемо цей зв'язок між відносною початковою та кінцевою швидкостями одновимірним принципом енергії-імпульсу, оскільки ми об'єднали ці два принципи, щоб реалізувати цей результат. Принцип енергії-імпульсу не залежить від мас стикаються частинок.

Хоча ми вивели цей результат явно, ми вже показали, що зміна кінетичної енергії для двочастинкової взаємодії (Equation (15.2.20)), в нашому спрощеному позначенні задається

\[\Delta K=\frac{1}{2} \mu\left(\left(v^{\mathrm{rel}}\right)_{f}^{2}-\left(v^{\mathrm{rel}}\right)_{i}^{2}\right) \nonumber \]

Тому для пружного зіткнення\(\Delta K=0\), де, квадрат відносної швидкості залишається постійним

\[\left(v^{\mathrm{rel}}\right)_{f}^{2}=\left(v^{\mathrm{rel}}\right)_{i}^{2} \nonumber \]

При одновимірному зіткненні величина відносної швидкості залишається постійною, але напрямок змінюється на\(180^{\circ}\).

Тепер ми можемо вирішити для остаточної x -складової швидкостей,\(v_{1 x, f}\) і\(\mathcal{V}_{2 x, f}\) наступним чином. Рівняння (15.3.7) можна переписати як

\[v_{2 x, f}=v_{1 x, f}+v_{1 x, i}-v_{2 x, i} \nonumber \]

Тепер замініть рівняння (15.3.12) на рівняння (15.3.1), що дає

\[m_{1} v_{1 x, i}+m_{2} v_{2 x, i}=m_{1} v_{1 x, f}+m_{2}\left(v_{1 x, f}+v_{1 x, i}-v_{2 x, i}\right) \nonumber \]

Розв'язування рівняння (15.3.13) для\(v_{1 x, f}\) включає деякі алгебри та виходи

\[v_{1 x, f}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}} v_{1 x, i}+\frac{2 m_{2}}{m_{1}+m_{2}} v_{2 x, i} \nonumber \]

Щоб знайти\(v_{2 x, f}\), перепишіть рівняння (15.3.7) як

\[v_{1 x, f}=v_{2 x, f}-v_{1 x, i}+v_{2 x, i} \nonumber \]

Тепер замініть рівняння (15.3.15) на рівняння (15.3.1), що дає

\[m_{1} v_{1 x, i}+m_{2} v_{2 x, i}=m_{1}\left(v_{2 x, f}-v_{1 x, i}+v_{2 x, i}\right) v_{1 x, f}+m_{2} v_{2 x, f} \nonumber \]

Ми можемо вирішити рівняння (15.3.16) для\(v_{2 x, f}\) і визначити, що

\[v_{2 x, f}=v_{2 x, i} \frac{m_{2}-m_{1}}{m_{2}+m_{1}}+v_{1 x, i} \frac{2 m_{1}}{m_{2}+m_{1}} \nonumber \]

Розглянемо, що відбувається\(m_{1} \gg m_{2}\) в межах Рівняння (15.3.14). Тоді

\[v_{1 x, f} \rightarrow v_{1 x, i}+\frac{2}{m_{1}} m_{2} v_{2 x, i} \nonumber \]

більш масивний компонент швидкості об'єкта лише трохи змінюється на величину, пропорційну x -компоненту імпульсу менш масивного об'єкта. Аналогічно наближається кінцева швидкість менш масивного об'єкта

\[v_{2 x, f} \rightarrow-v_{2 x, i}+2 v_{1 x, i}=v_{1 x, i}+v_{1 x, i}-v_{2 x, i} \nonumber \]

Ми можемо переписати це як

\[v_{2 x, f}-v_{1 x, i}=v_{1 x, i}-v_{2 x, i}=v_{x, i}^{\mathrm{rel}} \nonumber \]

тобто менш масивний об'єкт «відскакує» з тією ж швидкістю щодо більш масивного об'єкта, який ледве змінював свою швидкість.

Якщо об'єкти ідентичні або мають однакову масу, рівняння (15.3.14) та (15.3.17) стають

\[v_{1 x, f}=v_{2 x, i}, \quad v_{2 x, f}=v_{1 x, i} \nonumber \]

Об'єкти обмінялися x -складовими швидкостей, і якщо ми не могли якось розрізнити об'єкти, ми могли б не бути в змозі сказати, чи було зіткнення взагалі.

Одновимірне зіткнення між двома об'єктами - контрольний кадр центру маси

Ми проаналізували одновимірне пружне зіткнення (рис. 15.5) в розділі 15.4.1 в лабораторній системі відліку. Тепер давайте розглянемо зіткнення з кадру центру маси (CM). x -складова швидкості центру маси дорівнює

\[v_{x, \mathrm{cm}}=\frac{m_{1} v_{1 x, i}+m_{2} v_{2 x, i}}{m_{1}+m_{2}} \nonumber \]

Відносно центру маси x -складовими швидкостей об'єктів є

\ [\ почати {масив} {l}
v_ {1 x, i} ^ {\ прайм} =v_ {1 x, i} -v_ {x,\ mathrm {см}} =\ лівий (v_ {1 x, i} -v_ {2 x, i}\ правий)\ frac {m_ {2}}} {m_ {1} +m_ {2}\\
v_ {2 x, i} ^ {\ прайм} =v_ {2 x, i} -v_ {x,\ mathrm {см}} =\ лівий (v_ {2 x, i} -v_ {1 x, i}\ правий)\ frac {m_ {1}} {m_ {1} +m_ {2}}
\ кінець {масив}\ номер\]

У кадрі CM імпульс системи дорівнює нулю до зіткнення і, отже, імпульс системи дорівнює нулю після зіткнення. Для пружного зіткнення єдиним способом, щоб імпульс і кінетична енергія були однаковими до і після зіткнення, є або об'єкти мають однакову швидкість (промах), або змінити напрямок швидкостей, як показано на малюнку 15.6.

Рисунок 15.6 Одновимірне пружне зіткнення в рамці відліку центру маси

У рамці СМ кінцевими x -складовими швидкостей є

\ [\ почати {масив} {l}
v_ {1 x, f} ^ {\ прайм} =-v_ {1 x, i} ^ {\ прайм} =\ лівий (v_ {2 x, i} -v_ {1 x, i}\ правий)\ frac {m_ {2}} {m_ {1} +m_ {2}}\
v_ {2 x, f} ^ {\ прайм} =-v_ {2 x, i} ^ {\ прайм} =\ лівий (v_ {2 x, i} -v_ {1 x, i}\ правий)\ frac {m_ {1}} {m_ {1} +m_ {2}}
\ кінець {масив}\ nonumber\]

Остаточні x -складові швидкостей в «лабораторному кадрі» потім задаються

\ [\ почати {вирівняний}
v_ {1 x, f} &=v_ {1 x, f} ^ {\ прайм} +v_ {x,\ mathrm {см}}\\
&=\ лівий (v_ {2 x, i} -v_ {1 x, i}\ правий)\ frac {m_ {2}} {m_ {1} +m_ {2} +\ розрив {m_ {1} v_ {1 x, i} +м_ {2} v_ {2 x, i}} {m_ {1} +m_ {2}}\\
&=v_ {1 x, i}\ frac {m_ {1} -m_ {2}} {m_ {1} +m_ {2}} +v_ {2} i}\ Фракція {2 m_ {2}} {m_ {1} +m_ {2}}
\ кінець {вирівняний}\ nonumber\]

як у Рівнянні (15.3.14) і аналогічний розрахунок відтворює Рівняння (15.3.17).