14.6: Енергетична діаграма сили пружини

Сила пружини на об'єкті - це відновлювальна сила,\(\overrightarrow{\mathbf{F}}^{s}=F_{x}^{s} \hat{\mathbf{i}}=-k x \hat{\mathbf{i}}\) де ми вибираємо систему координат з положенням рівноваги в\(x_{i}=0\) і х - величина пружини розтягнута\((x>0)\) або стиснута\((x<0)\) з положення рівноваги. Обчислили рівняння різниці потенціалів енергії (14.4.9) і виявили, що

\[U^{s}(x)-U^{s}\left(x_{i}\right)=-\int_{x_{i}}^{x} F_{x}^{s} d x=\frac{1}{2} k\left(x^{2}-x_{i}^{2}\right) \nonumber \]

Перша фундаментальна теорема числення стверджує, що

\[U(x)-U\left(x_{i}\right)=\int_{x^{\prime}=x_{i}} x^{x^{\prime}=x} \frac{d U}{d x^{\prime}} d x^{\prime} \nonumber \]

Порівняння рівняння (14.5.1) з рівнянням (14.5.2) показує, що сила є негативною похідною (щодо положення) потенційної енергії,

\[F_{x}^{s}=-\frac{d U^{s}(x)}{d x} \nonumber \]

Виберіть нульову опорну точку для потенційної енергії, щоб бути в положенні рівноваги,\(U^{s}(0) \equiv 0\) Тоді функція потенційної енергії стає

\(U^{s}(x)=\frac{1}{2} k x^{2}\)

\[F_{x}^{s}=-\frac{d U^{s}(x)}{d x}=-\frac{d}{d x}\left(\frac{1}{2} k x^{2}\right)=-k x \nonumber \]

На малюнку 14.9 ми будуємо потенційну енергетичну функцію\(U^{s}(x)\) для сили пружини як функцію x з\(U^{s}(0) \equiv 0\) (одиниці довільні).

Рисунок 14.9 Графік функції потенційної енергії як функції x для пружини.

Мінімум потенційної енергетичної функції виникає в точці зникнення першої похідної

\(\frac{d U^{s}(x)}{d x}=0\)

З Рівняння (14.5.4) мінімум відбувається при х = 0,

\[0=\frac{d U^{s}(x)}{d x}=k x \nonumber \]

Оскільки сила є негативною похідною потенційної енергії, і ця похідна зникає на мінімумі, ми маємо, що сила пружини дорівнює нулю при мінімумі,\(x=0\) узгоджуючись з нашим законом сили,\(\left.F_{x}^{s}\right|_{x=0}=-\left.k x\right|_{x=0}=0\).

Функція потенційної енергії має позитивну кривизну в районі мінімальної точки рівноваги. Якщо об'єкт витягнутий на невелику відстань\(x>0\) від рівноваги, нахил потенційної енергетичної функції є позитивним\(d U(x) / d x>0\), отже, складова сили негативна тому що\(F_{x}=-d U(x) / d x<0\). Таким чином об'єкт відчуває відновлювальну силу до мінімальної точки потенціалу. Якщо об'єкт стискається з\(x<0\) потім\(d U(x) / d x<0\), отже, складова сили позитивна,\(F_{x}=-d U(x) / d x>0\) і об'єкт знову відчуває відновлювальну силу назад до мінімуму потенційної енергії, як на малюнку 14.10.

Малюнок 14.10 Діаграма стійкості сили пружини

Механічна енергія в будь-який момент - це сума кінетичної енергії K x () і потенційної енергії\(U^{s}(x)\)

\(E_{m}=K(x)+U^{s}(x)\)

Припустимо, наша система пружинних об'єктів не має втрат механічної енергії внаслідок дисипативних сил, таких як тертя або опір повітря. І кінетична енергія, і потенційна енергія є функціями положення об'єкта щодо рівноваги. Енергія є постійною руху і при нашому виборі\(U^{s}(0) \equiv 0\), енергія може бути як позитивним значенням, так і нулем. Коли енергія дорівнює нулю, об'єкт знаходиться в стані спокою в положенні рівноваги.

На малюнку 14.10 проведемо пряму горизонтальну лінію, відповідну ненульовому позитивному значенню для енергії\(E_{m}\) на графіку потенційної енергії як функції х. Енергія перетинає потенційну енергетичну функцію в двох точках\(\left\{-x_{\max }, x_{\max }\right\} \text { with } x_{\max }>0\). Ці точки відповідають максимальному стисненню і максимальному розтягуванню пружини, які називаються поворотними точками. Кінетична енергія - це різниця між енергією та потенційною енергією,

\[K(x)=E_{m}-U^{s}(x) \nonumber \]

У поворотних точках, де\(E_{m}=U^{s}(x)\), кінетична енергія дорівнює нулю. Регіони, де кінетична енергія негативна,\(x<-x_{\max } \text { or } x>x_{\max }\) називають класично забороненими областями, до яких об'єкт ніколи не може досягти, якщо підпорядковуватися законам класичної механіки. У квантовій механіці при подібних енергетичних діаграмах для квантових систем існує дуже мала ймовірність того, що квантовий об'єкт можна знайти в класично забороненій області.

Приклад 14.1 Енергетична діаграма

Функція потенційної енергії для частинки маси m, що рухається у напрямку x, задається

\[U(x)=-U_{1}\left(\left(\frac{x}{x_{1}}\right)^{3}-\left(\frac{x}{x_{1}}\right)^{2}\right) \nonumber \]

де\(U_{1}\) і\(x_{1}\) є позитивними константами і\(U(0)=0\). (a) Ескіз\(U(x) / U_{1}\) як функція\(x / x_{1}\). (б) Знайдіть точки, де сила на частку дорівнює нулю. Класифікують їх як стабільні або нестабільні. Обчисліть значення\(U(x) / U_{1}\) в цих точках рівноваги. (c) Для енергій Е, що лежить в\(0<E<(4 / 27) U_{1}\) знайти рівняння, рішення якого дає поворотні точки вздовж осі x, навколо якої частинка буде піддаватися періодичному руху. (d) Припустимо,\(E=(4 / 27) U_{1}\) і що частка починається\(x=0\) зі швидкістю\(v_{0}\). Знайти\(v_{0}\).

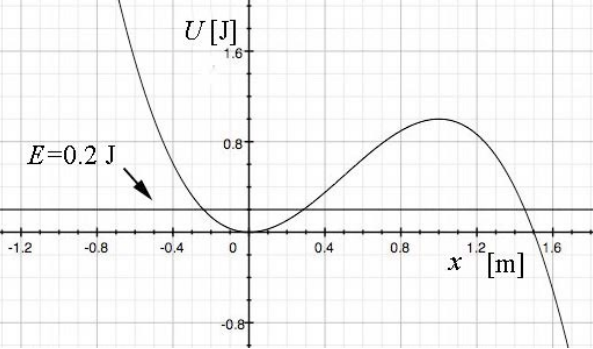
Рішення: а) на малюнку 14.11 показаний графік U (x) проти x, з вибором значень\(x_{1}=1.5 \mathrm{m}\)\(U_{1}=27 / 4 \mathrm{J}, \text { and } E=0.2 \mathrm{J}\).

Малюнок 14.11 Енергетична діаграма для прикладу 14.1

б) Сила на частинці дорівнює нулю при мінімумі потенціалу, який виникає при

\[F_{x}(x)=-\frac{d U}{d x}(x)=U_{1}\left(\left(\frac{3}{x_{1}^{3}}\right) x^{2}-\left(\frac{2}{x_{1}^{2}}\right) x\right)=0 \nonumber \]

який стає

\[x^{2}=\left(2 x_{1} / 3\right) x \nonumber \]

Ми можемо вирішити Рівняння (14.5.12) для крайності. Це має два рішення

\(x=\left(2 x_{1} / 3\right)\)і\ (\\ begin {рівняння} x = 0\ кінець {рівняння})

Друга похідна дається

\[\frac{d^{2} U}{d x^{2}}(x)=-U_{1}\left(\left(\frac{6}{x_{1}^{3}}\right) x-\left(\frac{2}{x_{1}^{2}}\right)\right) \nonumber \]

Оцінка другої похідної при\(x=\left(2 x_{1} / 3\right)\) отриманні негативної величини

\[\frac{d^{2} U}{d x^{2}}\left(x=\left(2 x_{1} / 3\right)\right)=-U_{1}\left(\left(\frac{6}{x_{1}^{3}}\right) \frac{2 x_{1}}{3}-\left(\frac{2}{x_{1}^{2}}\right)\right)=-\frac{2 U_{1}}{x_{1}^{2}}<0 \nonumber \]

вказує на рішення\(x=\left(2 x_{1} / 3\right)\) являє собою локальний максимум і, отже, є нестабільною точкою. При\(x=\left(2 x_{1} / 3\right)\), потенційна енергія задається величиною\(U\left(\left(2 x_{1} / 3\right)\right)=(4 / 27) U_{1}\). Оцінка другої похідної при x = 0 дає позитивну величину

\[\frac{d^{2} U}{d x^{2}}(x=0)=-U_{1}\left(\left(\frac{6}{x_{1}^{3}}\right) 0-\left(\frac{2}{x_{1}^{2}}\right)\right)=\frac{2 U_{1}}{x_{1}^{2}}>0 \nonumber \]

вказуючи розв'язку x=0, є локальним мінімумом і є стабільною точкою. При локальному мінімумі x = 0 потенційна енергія U (0) = 0.

в) Розглянемо фіксоване значення енергії частинки в межах діапазону

\[U(0)=0<E<U\left(2 x_{1} / 3\right)=\frac{4 U_{1}}{27} \nonumber \]

Якщо частинка в будь-який момент знаходиться в тій області\(x_{a}<x<x_{b}<2 x_{1} / 3\), де\(x_{a}\) і\(x_{b}\) знаходяться поворотні точки і є розв'язками рівняння

\[E=U(x)=-U_{1}\left(\left(\frac{x}{x_{1}}\right)^{3}-\left(\frac{x}{x_{1}}\right)^{2}\right) \nonumber \]

тоді частка буде піддаватися періодичному руху між значеннями\(x_{a}<x<x_{b}\). У межах цієї області кінетична енергія завжди позитивна\(x_{a}<x<x_{b}\), тому що\(K(x)=E-U(x)\) існує інше рішення\(x_{c}\) рівняння (14.5.18) десь у регіоні\(x_{c}>2 x_{1} / 3\). Якщо частка в будь-який час знаходиться в регіоні,\(x>x_{c}\) то вона в будь-який більш пізній час обмежується регіоном\(x_{c}<x<+\infty\).

Для\(E>U\left(2 x_{1} / 3\right)=(4 / 27) U_{1}\), Рівняння (14.5.18) має тільки одне рішення\(x_{d}\). Для всіх значень кінетична енергія є позитивною\(x>x_{d}\), що означає, що частинка може «втекти» до нескінченності, але ніколи не може увійти в область\(x<x_{d}\).

Для\(E<U(0)=0\) кінетичної енергії є негативною для діапазону,\(-\infty<x<x_{e}\) де\(x_{e}\) задовольняє Рівняння (14.5.18) і тому ця область простору заборонена.

(d) Якщо частинка має швидкість\(v_{0}\) при x = 0, де потенційна енергія дорівнює нулю\(U(0)=0\), енергія частинки постійна і дорівнює кінетичній енергії

\[E=K(0)=\frac{1}{2} m v_{0}^{2} \nonumber \]

Тому

\[(4 / 27) U_{1}=\frac{1}{2} m v_{0}^{2} \nonumber \]

які ми можемо вирішити для швидкості

\[v_{0}=\sqrt{8 U_{1} / 27 m} \nonumber \]