Skip to main content
LibreTexts - Ukrayinska

13.5: Робота, виконана непостійними силами

  1. Last updated
  2. Save as PDF
  • Page ID
    75891

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розглянемо тіло, що рухається в х -напрямку під впливом непостійної сили в х -напрямку,\(\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}\). Тіло переміщається з вихідного положення\(x_{i}\) в кінцеве положення\(x_{f}\). Для того щоб обчислити роботу, виконану непостійною силою, розділимо зміщення точки прикладання сили на велику кількість N малих переміщень,\(\Delta x_{j}\) де індекс j позначає\(j_{th}\) зсув і приймає ціле значення від 1 до N. \(\left(F_{x, j}\right)_{\text {ave }}\)Дозвольте позначити середнє значення х -складової сили в інтервалі зміщення\(\left[x_{j-1}, x_{j}\right]\). Для інтервалу\(j_{th}\) зміщення розраховуємо внесок в роботу.

    \[W_{j}=\left(F_{x, j}\right)_{\text {ave }} \Delta x_{j} \nonumber \]

    Цей внесок є скалярним, тому ми складаємо ці скалярні величини, щоб отримати загальну роботу.

    \[W_{N}=\sum_{j=1}^{j=N} W_{j}=\sum_{j=1}^{j=N}\left(F_{x, j}\right)_{\text {ave }} \Delta x_{j} \nonumber \]

    Сума в Рівнянні (13.5.2) залежить від кількості ділень N і ширини інтервалів\(\Delta x_{j}\). Для того, щоб визначити величину, яка не залежить від поділів, беремо ліміт як\(N \rightarrow \infty\) і\(\left|\Delta x_{j}\right| \rightarrow 0\) для всіх j. Робота тоді

    \[W=\lim _{N \rightarrow \infty \atop\left|\Delta x_{j}\right| \rightarrow 0} \sum_{j=1}^{j=N}\left(F_{x, j}\right)_{\text {ave }} \Delta x_{j}=\int_{x=x_{i}}^{x=x_{f}} F_{x}(x) d x \nonumber \]

    Цей останній вираз є певним інтегралом х -складової сили по відношенню до параметра x. На малюнку 13.5 ми графуємо х -складову сили як функцію параметра x. Робочий інтеграл - це площа під цією кривою між\(x=x_{i}\) і\(x=x_{f}\).

    clipboard_e1155a01d2f1a63c5b81abc028f084471.png
    Малюнок 13.5 Ділянка x -складової сили вибірки\(F_{x}(x)\) як функції x.

    Приклад\(\PageIndex{1}\): Work done by the Spring Force

    З'єднайте один кінець нерозтягнутої пружини довжиною\(l_{0}\) з постійною пружини k до предмета, що спирається на плавний стіл без тертя, і закріпіть інший кінець пружини до стіни. Виберіть походження, як показано на малюнку. Розтягніть пружину на суму\(x_{i}\) і відпустіть предмет. Скільки роботи робить пружина на об'єкті, коли пружина розтягується на суму\(x_{f}\)?

    clipboard_ecdbf66e45e8ba4a240783bf0e335b8b9.png
    Малюнок 13.6 Рівновага, початковий і кінцевий стани для пружини

    Рішення

    Спочатку ми починаємо з вибору системи координат з нашим початком, розташованим в положенні об'єкта, коли пружина нерозтягнута (або нестиснута). Ми вибираємо\(\hat{\mathbf{i}}\) одиничний вектор, щоб вказувати в напрямку руху об'єкта при розтягуванні пружини. Вибираємо координатну функцію x для позначення положення об'єкта щодо початку. Ми показуємо координатну функцію та діаграму сили вільного тіла на малюнку нижче.

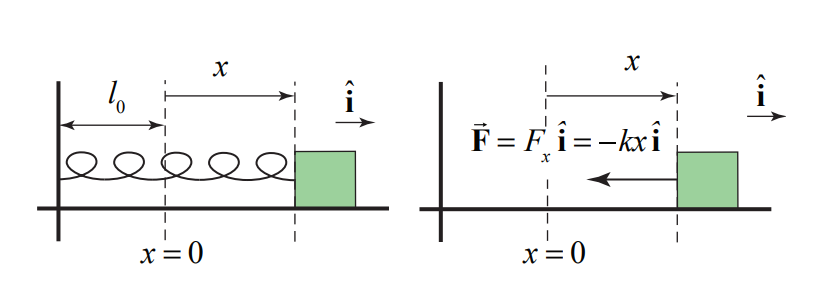
    clipboard_e8a8779cc6b6ac9de0dd64fa02e0f5fb8.png
    Малюнок 13.6a Сили пружини

    Сила пружини на об'єкт задається (рис. 13.6а)

    \[\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}=-k x \hat{\mathbf{i}} \nonumber \]

    На малюнку 13.7 ми показуємо графік х -складової сили пружини\(F_{x}(x)\), як функція х

    clipboard_e4d17b7e3d71ce6401c162953442ea8c7.png
    Малюнок 13.7 Ділянка сили пружини\(F_{x}(x)\) проти зміщення x

    Проведена робота - це якраз площа під кривою для інтервалу\(x_{i}\) до\(x_{f}\),

    \[W=\int_{x^{\prime}=x_{i}}^{x^{\prime}=x_{f}} F_{x}\left(x^{\prime}\right) d x^{\prime}=\int_{x^{\prime}=x_{i}}^{x^{\prime}=x_{f}}-k x^{\prime} d x^{\prime}=-\frac{1}{2} k\left(x_{f}^{2}-x_{i}^{2}\right) \nonumber \]

    Цей результат не залежить від знака\(x_{i}\) і\(x_{f}\) тому, що обидві величини виглядають як квадрати. Якщо пружина менш розтягнута або стиснута в кінцевому стані, ніж в початковому стані, то абсолютне значення,\(\left|x_{f}\right|<\left|x_{i}\right|\) а робота, виконана силою пружини, позитивна. Сила пружини робить позитивну роботу на тілі, коли пружина переходить зі стану «більшої напруги» в стан «меншого натягу».