13.4: Робота, виконана постійними силами
- Page ID
- 75903
Ми почнемо наше обговорення концепції роботи з аналізу руху об'єкта в одному вимірі, на який діють постійні сили. Розглянемо наступний приклад: висуньте чашку вперед з постійною силою уздовж робочого столу. Коли чаша змінює швидкість (а значить і кінетичну енергію), сума сил, що діють на чашу, повинна бути ненульовою відповідно до Другого закону Ньютона. У цьому русі беруть участь три сили: прикладена сила штовхання\(\overrightarrow{\mathbf{F}}^{a}\); контактна сила\(\overrightarrow{\mathbf{C}} \equiv \overrightarrow{\mathbf{N}}+\overrightarrow{\mathbf{f}}_{k}\); і гравітація\(\overrightarrow{\mathbf{F}}^{g}=m \overrightarrow{\mathbf{g}}\). Схема сили на чашці показана на малюнку 13.2.

Давайте виберемо нашу систему координат так, що +x -напрямок - це напрямок руху чашки вперед. Потім сила натискання може бути описана
\[\overrightarrow{\mathbf{F}}^{a}=F_{x}^{a} \hat{\mathbf{i}} \nonumber \]
Припустимо, що тіло рухається від початкової точки\(x_{i}\) до кінцевої точки\(x_{f}\) так, що зміщення точки, на яку діє сила\(\Delta x \equiv x_{f}-x_{i}\). Робота, виконана постійною силою, що\(\overrightarrow{\mathbf{F}}^{a}=F_{x}^{a} \hat{\mathbf{i}}\) діє на тіло, є твором складової сили\(F_{x}^{a}\) і зміщення Δx,
\[W^{a}=F_{x}^{a} \Delta x \nonumber \]
Робота - це скалярна величина; це не векторна величина. Одиницею СІ для роботи є
\[[1 \mathrm{N} \cdot \mathrm{m}]=\left[1 \mathrm{kg} \cdot \mathrm{m} \cdot \mathrm{s}^{-2}\right][1 \mathrm{m}]=\left[1 \mathrm{kg} \cdot \mathrm{m}^{2} \cdot \mathrm{s}^{-2}\right]=[1 \mathrm{J}] \nonumber \]
Зверніть увагу, що робота має таку ж розмірність і ту ж одиницю СІ, що і кінетична енергія. Оскільки наша прикладена сила знаходиться уздовж напрямку руху,\(F_{x}^{a}>0\) і\(\Delta x>0\) в цьому прикладі виконана робота є лише добутком величини прикладеної сили та відстані, через яку діє ця сила і є позитивною. При визначенні роботи, виконаної силою, сила може діяти в будь-якій точці на тілі. Зсув, який з'являється в Рівнянні (13.4.2) - це не зміщення тіла, а зміщення точки прикладання сили. Для точкових предметів зміщення точки прикладання сили дорівнює зміщенню тіла. Однак для розширеного тіла нам потрібно зосередитись на тому, де діє сила, і чи зазнає ця точка застосування будь-якого зміщення у напрямку сили, як показано на наступному прикладі.
Приклад 13.2 Робота, виконана статичною художньою літературою
Припустимо, ви спочатку стоїте і починаєте ходити, штовхаючись на землю ногами, а ноги не ковзають. Яка робота виконується статичною силою тертя, що діє на вас?
Рішення: Коли ви застосовуєте контактну силу до землі, земля прикладає до вас рівну і протилежну контактну силу. Тангенціальна складова цієї постійної сили - сила статичного тертя, що діє на вас. Оскільки ваша нога знаходиться в стані спокою, поки ви штовхаєтеся об землю, немає зміщення точки прикладання цієї статичної сили тертя. Тому статичне тертя робить нуль працювати на вас, поки ви прискорюєтеся. Ви можете бути здивовані цим результатом, але якщо ви думаєте про перетворення енергії, хімічна енергія, що зберігається у ваших м'язових клітинок, перетворюється в кінетичну енергію руху та теплову енергію.
Коли сили протистоять руху, як у нашому прикладі штовхання чашки, кінетична сила тертя задається
\[\overrightarrow{\mathbf{F}}^{f}=f_{k, x} \hat{\mathbf{i}}=-\mu_{k} N \hat{\mathbf{i}}=-\mu_{k} m g \hat{\mathbf{i}} \nonumber \]
Тут складова сили знаходиться в зворотному напрямку, як і зміщення. Робота, виконана кінетичною силою тертя, негативна,
\[W^{f}=-\mu_{k} m g \Delta x \nonumber \]
Оскільки сила тяжіння перпендикулярна руху чашки, гравітаційна сила не має складової уздовж лінії руху. Тому сила тяжіння робить нульову роботу на чашці, коли чашка ковзає вперед у горизонтальному напрямку. Нормальна сила також перпендикулярна руху, а значить, не працює.
Ми бачимо, що сила штовхання робить позитивну роботу, кінетична сила тертя робить негативну роботу, а гравітація та нормальна сила роблять нульову роботу.
Приклад 13.3 Робота, виконана силою, прикладеною у напрямку переміщення
Просуньте чашку масою 0,2 кг уздовж горизонтального столу з силою величиною 2,0 Н на відстань 0,5 м. коефіцієнт тертя між столом і чашею\(\mu_{k}=0.10\) Розрахуйте роботу, виконану силою штовхання і роботою, виконаної силою тертя.
Рішення: Робота, виконана силою натискання, є
\[W^{a}=F_{x}^{a} \Delta x=(2.0 \mathrm{N})(0.5 \mathrm{m})=1.0 \mathrm{J} \nonumber \]
Робота, виконана силою тертя, є
\[W^{f}=-\mu_{k} m g \Delta x=-(0.1)(0.2 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)(0.5 \mathrm{m})=-0.10 \mathrm{J} \nonumber \]
Приклад 13.4 Робота, виконана силою, прикладеною під кутом до напрямку переміщення
Припустимо, ми штовхаємо чашку в попередньому прикладі з силою тієї ж величини, але під кутом\(\theta=30^{\circ}\) вгору по відношенню до столу. Розрахуйте роботу, виконану силою натискання. Розрахуйте виконану роботу по кінетичній силі тертя.
Рішення: Діаграма сили на чашці і системі координат показана на малюнку 13.3.
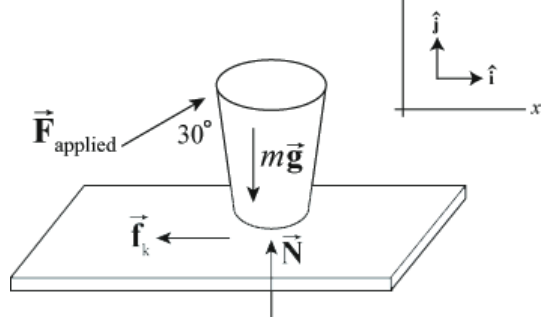
X -компонент сили натискання тепер
\[F_{x}^{a}=F^{a} \cos (\theta)=(2.0 \mathrm{N})\left(\cos \left(30^{\circ}\right)\right)=1.7 \mathrm{N} \nonumber \]
Робота, виконана силою натискання, є
\[W^{a}=F_{x}^{a} \Delta x=(1.7 \mathrm{N})(0.5 \mathrm{m})=8.7 \times 10^{-1} \mathrm{J} \nonumber \]
Кінетична сила тертя дорівнює
\[\overrightarrow{\mathbf{F}}^{f}=-\mu_{k} N \hat{\mathbf{i}} \nonumber \]
При цьому величина нормальної сили не просто така ж, як вага чашки. Нам потрібно знайти y -складову прикладеної сили,
\[F_{y}^{a}=F^{a} \sin (\theta)=(2.0 \mathrm{N})\left(\sin \left(30^{\circ}\right)=1.0 \mathrm{N}\right. \nonumber \]
Щоб знайти нормальну силу, застосуємо Другий закон Ньютона в напрямку y,
\[F_{y}^{a}+N-m g=0 \nonumber \]
Тоді нормальна сила
\[N=m g-F_{y}^{a}=(0.2 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)-(1.0 \mathrm{N})=9.6 \times 10^{-1} \mathrm{N} \nonumber \]
Робота, виконана кінетичною силою тертя, є
\[W^{f}=-\mu_{k} N \Delta x=-(0.1)\left(9.6 \times 10^{-1} \mathrm{N}\right)(0.5 \mathrm{m})=4.8 \times 10^{-2} \mathrm{J} \nonumber \]
Приклад 13.5 Робота, виконана гравітацією поблизу поверхні Землі
Розглянемо точкове тіло масою m біля поверхні землі, що падає безпосередньо до центру землі. Сила тяжіння між тілом і землею майже постійна,\(\overrightarrow{\mathbf{F}}_{g r a v}=m \overrightarrow{\mathbf{g}}\). Давайте виберемо систему координат з початком на поверхні землі та напрямком + y, спрямованим від центру землі Припустимо, що тіло починається з початкової точки\(y_{i}\) і падає до кінцевої точки\(y_{f}\) ближче до землі. Скільки роботи сила тяжіння робить на тілі, коли воно падає?
Рішення: Зсув тіла негативний,\(\Delta y \equiv y_{f}-y_{i}<0\). Сила тяжіння задається
\[\overrightarrow{\mathbf{F}}^{g}=m \overrightarrow{\mathbf{g}}=F_{y}^{g} \hat{\mathbf{j}}=-m g \hat{\mathbf{j}} \nonumber \]
Робота, виконана над тілом, є тоді
\[W^{g}=F_{y}^{g} \Delta y=-m g \Delta y \nonumber \]
Для падаючого тіла зміщення тіла є негативним, тому робота\(\Delta y \equiv y_{f}-y_{i}<0\), виконана гравітацією, позитивна,\(W^{g}>0\). Сила тяжіння спрямована в тому ж напрямку, що і зміщення падаючого об'єкта, тому робота повинна бути позитивною.
Коли об'єкт піднімається під впливом сили тяжіння,\(\Delta y \equiv y_{f}-y_{i}>0\). Робота, виконана силою тяжіння для висхідного тіла, є негативною\(W^{g}<0\), оскільки сила тяжіння спрямована в протилежному напрямку від тієї, в якій об'єкт зміщується.
Важливо відзначити, що вибір позитивного напрямку як віддалення від центру землі («вгору») не має значення. Якби напрямок вниз було обрано позитивним, падаюче тіло матиме позитивне зміщення, а гравітаційна сила, як зазначено в Рівнянні (13.4.15), мала б позитивний спадний компонент; продукт все одно\(F_{y}^{g} \Delta y\) був би позитивним.
