12.2: Опрацьовані приклади
- Page ID
- 75327
Приклад\(\PageIndex{1}\): Filling a Coal Car
Порожня вугільна машина маси\(m_{0}\) починається з спокою під прикладеною силою величиною F. При цьому вугілля починає набігати в вагон зі стійкою швидкістю б з вугільного бункера в спокої уздовж колії (рис. 12.5). Знайдіть швидкість, коли була передана маса\(m_{c}\) вугілля.
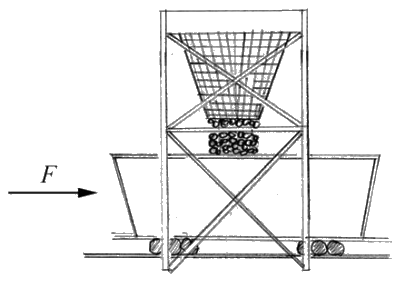
Рішення
Розберемо зміни імпульсу в горизонтальному напрямку, яке ми називаємо х -напрямком. Оскільки падаюче вугілля не має горизонтальної швидкості, падаючий вугілля не передає жодного імпульсу в напрямку x до вугільної машини. Тож ми візьмемо за нашу систему порожній вугільний автомобіль і\(m_{c}\) масу вугілля, яке було передано. Наш початковий стан при t = 0 - це коли вугільний автомобіль порожній і знаходиться в стані спокою, перш ніж будь-яке вугілля було передано. x -складова імпульсу цього початкового стану дорівнює нулю,
\[p_{x}(0)=0 \nonumber \]
Наш остаточний стан\(t=t_{f}\) - це коли все вугілля маси\(m_{c}=b t_{f}\) було передано в машину, яка зараз рухається зі швидкістю\(v_{f}\). Х -складова імпульсу цього кінцевого стану дорівнює
\[p_{x}\left(t_{f}\right)=\left(m_{0}+m_{c}\right) v_{f}=\left(m_{0}+b t_{f}\right) v_{f} \nonumber \]
Існує зовнішня постійна сила, що\(F_{x}=F\) додається через передачу. Принцип імпульсу, застосований до x -direction, є
\[\int_{0}^{t_{f}} F_{x} d t=\Delta p_{x}=p_{x}\left(t_{f}\right)-p_{x}(0) \nonumber \]
Оскільки сила постійна, інтеграл простий, а принцип імпульсу стає
\[F t_{f}=\left(m_{0}+b t_{f}\right) v_{f} \nonumber \]
Отже, кінцева швидкість
\[v_{f}=\frac{F t_{f}}{\left(m_{0}+b t_{f}\right)} \nonumber \]
Приклад\(\PageIndex{2}\): Emptying a Freight Car
Вантажний вагон маси\(m_{c}\) містить пісок маси\(m_{s}\). При\(t=0\) постійній горизонтальній силі величини F прикладається в напрямку прокатки і одночасно відкривається отвір в дні, щоб пісок витік з постійною швидкістю\(b=d m_{s} / d t\). Знайти швидкість вантажного вагона, коли весь пісок пропаде (рис. 12.6). Припустимо, що вантажний вагон знаходиться в стані спокою на\(t=0\).

Рішення
Виберіть позитивний x -direction, щоб вказати напрямок руху автомобіля. Вибирайте для системи кількість піску в переляку автомобіля на час t,\(m_{c}(t)\). У момент t автомобіль рухається зі швидкістю\(\overrightarrow{\mathbf{v}}_{c}(t)=v_{c}(t) \hat{\mathbf{i}}\). Діаграма імпульсу для системи за час t показана на схемі зліва на малюнку 12.7.

Імпульс системи в момент t задається
\[\overrightarrow{\mathbf{p}}_{s y s}(t)=m_{c}(t) \overrightarrow{\mathbf{v}}_{c}(t) \nonumber \]
За\([t, t+\Delta t]\) часовий проміжок з вантажного вагона\(\Delta m_{s}\) виходить кількість піску маси і маса вантажного вагона змінюється на\(m_{c}(t+\Delta t)=m_{c}(t)+\Delta m_{c}\), де\(\Delta m_{c}=-\Delta m_{s}\). В кінці інтервалу автомобіль рухається зі швидкістю\(\overrightarrow{\mathbf{v}}_{c}(t+\Delta t)=\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}=\left(v_{c}(t)+\Delta v_{c}\right) \hat{\mathbf{i}}\). Діаграма імпульсу для системи в момент часу\(t+\Delta t\) показана на схемі праворуч на малюнку 12.7. Імпульс системи в часі\(t+\Delta t\) задається
\[\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)=\left(\Delta m_{s}+m_{c}(t)+\Delta m_{c}\right)\left(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\right)=m_{c}(t)\left(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\right) \nonumber \]
Зверніть увагу, що пісок, який залишає автомобіль, показаний зі швидкістю\(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\). Це має на увазі, що весь пісок залишає автомобіль зі швидкістю руху автомобіля в кінці інтервалу. Це наближення. Оскільки пісок залишає безперервним, швидкість буде змінюватися від\(\overrightarrow{\mathbf{v}}_{c}(t)\) до,\(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\) але так само зміна маси автомобіля, і ці два внески в момент системи точно скасовують. Зміна імпульсу системи тоді
\[\Delta \overrightarrow{\mathbf{p}}_{s y s}=\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)-\overrightarrow{\mathbf{p}}_{s y s}(t)=m_{c}(t)\left(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\right)-m_{c}(t) \overrightarrow{\mathbf{v}}_{c}(t)=m_{c}(t) \Delta \overrightarrow{\mathbf{v}}_{c} \nonumber \]
Протягом усього інтервалу до системи\(\overrightarrow{\mathbf{F}}=F \hat{\mathbf{i}}\) прикладається постійна сила, тому принцип імпульсу стає
\[\overrightarrow{\mathbf{F}}=\lim _{\Delta t \rightarrow 0} \frac{\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)-\overrightarrow{\mathbf{p}}_{s y s}(t)}{\Delta t}=\lim _{\Delta t \rightarrow 0} m_{c}(t) \frac{\Delta \overrightarrow{\mathbf{v}}_{c}}{\Delta t}=m_{c}(t) \frac{d \overrightarrow{\mathbf{v}}_{c}}{d t} \nonumber \]
Оскільки рух є одновимірним, рівняння (12.3.9), записане через x -компоненти, стає
\[F=m_{c}(t) \frac{d v_{c}}{d t} \nonumber \]
Позначають початковою масою автомобіля,\(m_{c, 0}=m_{c}+m_{s}\) де\(m_{c}\) маса автомобіля і\(m_{s}\) маса піску в машині при\(t=0\). Маса піску, що вийшов з машини на час t, задається
\[m_{s}(t)=\int_{0}^{t} \frac{d m_{s}}{d t} d t=\int_{0}^{t} b d t=b t \nonumber \]
Таким чином
\[m_{c}(t)=m_{c, 0}-b t=m_{c}+m_{s}-b t \nonumber \]
Тому рівняння (12.3.10) стає
\[F=\left(m_{c}+m_{s}-b t\right) \frac{d v_{c}}{d t} \nonumber \]
Це рівняння може бути вирішено для х -складової швидкості в момент t,\(v_{c}(t)\) (яка в даному випадку є швидкістю) методом поділу змінних. Перепишіть рівняння (12.3.13) як
\[d v_{c}=\frac{F d t}{\left(m_{c}+m_{s}-b t\right)} \nonumber \]
Потім інтегруйте обидві сторони рівняння (12.3.14) з межами, як показано на малюнку
\[\int_{v^{\prime}=0}^{v^{\prime}=v_{c}(t)} d v_{c}^{\prime}=\int_{t^{\prime}=0}^{t^{\prime}=t} \frac{F d t^{\prime}}{m_{c}+m_{s}-b t^{\prime}} \nonumber \]
Інтеграція дає швидкість автомобіля в залежності від часу
\[v_{c}(t)=-\left.\frac{F}{b} \ln \left(m_{c}+m_{s}-b t^{\prime}\right)\right|_{t=0} ^{\prime^{\prime}=t}=-\frac{F}{b} \ln \left(\frac{m_{c}+m_{s}-b t}{m_{c}+m_{s}}\right)=\frac{F}{b} \ln \left(\frac{m_{c}+m_{s}}{m_{c}+m_{s}-b t}\right) \nonumber \]
У написанні Equation (12.3.16) ми використовували властивість що\(\ln (a)-\ln (b)=\ln (a / b)\) і тому\(\ln (a / b)=-\ln (b / a)\). Відзначимо\(m_{c}+m_{s} \geq m_{c}+m_{s}-b t\), що, так термін\(\ln \left(\frac{m_{c}+m_{s}}{m_{c}+m_{s}-b t}\right) \geq 0\), і швидкість автомобіля збільшується так, як ми очікуємо.
Приклад\(\PageIndex{3}\): Filling a Freight Car
Зерно видувається в машину А з вагона Б зі швидкістю b кілограм в секунду. Зерно виходить з жолоба вертикально вниз, щоб воно мало таку ж горизонтальну швидкість, u, як і вагон Б, (рис. 12.8). Автомобіль А спочатку знаходиться в стані спокою перед тим, як будь-яке зерно буде передано в і має масу\(m_{A, 0}\). На даний момент, що цікавить, автомобіль А має масу\(m_{A}\) і швидкість v. Визначити вираз для швидкісного автомобіля А в залежності від часу t.
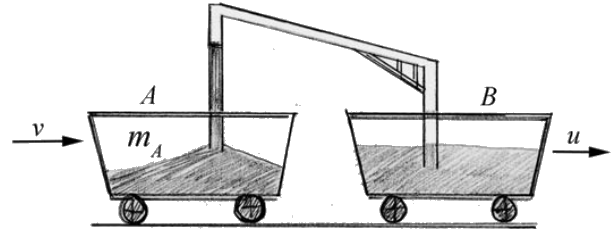
Рішення
Виберіть позитивний х -напрямок праворуч у напрямку руху автомобілів. Визначте систему в момент t, щоб бути автомобіль і зерно, яке вже знаходиться в ньому, яке разом має масу\(m_{A}(t)\) і невелику кількість матеріалу маси,\(\Delta m_{g}\) що видувається в автомобіль А протягом часового інтервалу\([t, t+\Delta t]\) В час, що рухається з х -складовою швидкості\(\mathcal{V}_{A}\). Під час t автомобіль А рухається зі швидкістю,\(\overrightarrow{\mathbf{v}}_{A}(t)=v_{A}(t) \hat{\mathbf{i}}\) а матеріал, що вдувається в машину, рухається зі\(\overrightarrow{\mathbf{u}}=u \hat{\mathbf{i}}\) швидкістю. У той час\(t+\Delta t\) автомобіль А рухається зі швидкістю\(\overrightarrow{\mathbf{v}}_{A}(t)+\Delta \overrightarrow{\mathbf{v}}_{A}=\left(v_{A}(t)+\Delta v_{A}\right) \hat{\mathbf{i}}\), а маса автомобіля А -\(m_{A}(t+\Delta t)=m_{A}(t)+\Delta m_{A}\) де\(\Delta m_{A}=\Delta m_{g}\). Діаграма імпульсу для разів t і for\(t+\Delta t\) показана на малюнку 12.9.

Імпульс на час t
\[\overrightarrow{\mathbf{P}}_{s y s}(t)=m_{A}(t) \overrightarrow{\mathbf{v}}_{A}(t)+\Delta m_{g} \overrightarrow{\mathbf{u}} \nonumber \]
Імпульс на\(t+\Delta t\) час
\[\overrightarrow{\mathbf{P}}_{s y s}(t+\Delta t)=\left(m_{A}(t)+\Delta m_{A}\right)\left(\overrightarrow{\mathbf{v}}_{A}(t)+\Delta \overrightarrow{\mathbf{v}}_{A}\right) \nonumber \]
Немає зовнішніх сил, що діють на систему в х -напрямку, і зовнішні сили, що діють на систему перпендикулярно сумі руху до нуля, тому принцип імпульсу стає
\[\overrightarrow{\mathbf{0}}=\lim _{\Delta t \rightarrow 0} \frac{\overrightarrow{\mathbf{P}}_{s y s}(t+\Delta t)-\overrightarrow{\mathbf{P}}_{s y s}(t)}{\Delta t} \nonumber \]
Використовуючи наведені вище результати (Рівняння (12.3.17) та (12.3.18), принцип імпульсу стає
\[\overrightarrow{\mathbf{0}}=\lim _{\Delta t \rightarrow 0} \frac{\left(m_{A}(t)+\Delta m_{A}\right)\left(\overrightarrow{\mathbf{v}}_{A}(t)+\Delta \overrightarrow{\mathbf{v}}_{A}\right)-\left(m_{A}(t) \overrightarrow{\mathbf{v}}_{A}(t)+\Delta m_{g} \overrightarrow{\mathbf{u}}\right)}{\Delta t} \nonumber \]
який після використання умови, що\(\Delta m_{A}=\Delta m_{g}\) і деяка перестановка стає
\[\overrightarrow{\mathbf{0}}=\lim _{\Delta t \rightarrow 0} \frac{m_{A}(t) \Delta \overrightarrow{\mathbf{v}}_{A}}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{A}\left(\overrightarrow{\mathbf{v}}_{A}(t)-\overrightarrow{\mathbf{u}}\right)}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{A} \Delta \overrightarrow{\mathbf{v}}_{A}}{\Delta t} \nonumber \]
У граничній якості добуток\(\Delta m_{A} \Delta \overrightarrow{\mathbf{V}}_{A}\) є диференціалом другого порядку (добуток двох диференціалів першого порядку), а термін\(\Delta m_{A} \Delta \overrightarrow{\mathbf{v}}_{A} / \Delta t\) наближається до нуля, тому принцип імпульсу дає диференціальне рівняння
\[\overrightarrow{\mathbf{0}}=m_{A}(t) \frac{d \overrightarrow{\mathbf{v}}_{A}}{d t}+\frac{d m_{A}}{d t}\left(\overrightarrow{\mathbf{v}}_{A}(t)-\overrightarrow{\mathbf{u}}\right) \nonumber \]
Тоді x -компонент рівняння (12.3.22)
\[0=m_{A}(t) \frac{d v_{A}}{d t}+\frac{d m_{A}}{d t}\left(v_{A}(t)-u\right) \nonumber \]
Переставляючи терміни і використовуючи той факт, що матеріал видувається в автомобіль А з постійною швидкістю\(b \equiv d m_{A} / d t\), ми маємо, що швидкість зміни х -складової швидкості автомобіля А задається
\[\frac{d v_{A}(t)}{d t}=\frac{b\left(u-v_{A}(t)\right)}{m_{A}(t)} \nonumber \]
Ми не можемо безпосередньо інтегрувати рівняння (12.3.24) щодо dt, оскільки маса автомобіля A є функцією часу. Для того, щоб знайти x -складову швидкості автомобіля А, нам потрібно знати залежність між масою автомобіля A і x -складовою швидкості автомобіля А. Є два підходи. У першому підході ми відокремлюємо змінні в Equation (12.3.24), де ми пригнічували залежність від t у виразах for\(m_{A}\) та\(\mathcal{V}_{A}\) firding
\[\frac{d v_{A}}{u-v_{A}}=\frac{d m_{A}}{m_{A}} \nonumber \]
який стає інтегральним рівнянням
\[\int_{v_{A}^{\prime}=0}^{v_{A}^{\prime}=v_{A}(t)} \frac{d v_{A}^{\prime}}{u-v_{A}^{\prime}}=\int_{m_{A}^{\prime}=m_{A, 0}}^{m_{A^{\prime}}^{\prime}=m_{A}(t)} \frac{d m_{A}^{\prime}}{m_{A}^{\prime}} \nonumber \]
де\(m_{A, 0}\) - маса автомобіля до того, як будь-який матеріал був видутий. Після інтеграції ми маємо це
\[\ln \frac{u}{u-v_{A}(t)}=\ln \frac{m_{A}(t)}{m_{A, 0}} \nonumber \]
Збільшити врожайність обох сторін
\[\frac{u}{u-v_{A}(t)}=\frac{m_{A}(t)}{m_{A, 0}} \nonumber \]
Ми можемо розв'язати це рівняння для х -складової швидкості автомобіля
\[v_{A}(t)=\frac{m_{A}(t)-m_{A, 0}}{m_{A}(t)} u \nonumber \]
Оскільки матеріал видувається в автомобіль з постійною швидкістю\(b \equiv d m_{A} / d t\), маса автомобіля як функція часу задається
\[m_{A}(t)=m_{A, 0}+b t \nonumber \]
Тому заміщення рівняння (12.3.30) у Рівняння (12.3.29) дає x -складову швидкості автомобіля як функцію часу
\[v_{A}(t)=\frac{b t}{m_{A, 0}+b t} u \nonumber \]
У другому підході ми замінюємо рівняння (12.3.30) на рівняння (12.3.24), що дає
\[\frac{d v_{A}}{d t}=\frac{b\left(u-v_{A}\right)}{m_{A, 0}+b t} \nonumber \]
Окремі змінні в рівнянні (12.3.32):
\[\frac{d v_{A}}{u-v_{A}}=\frac{b d t}{m_{A, 0}+b t} \nonumber \]
який потім стає інтегральним рівнянням
\[\int_{v_{A}^{\prime}=0}^{v_{A}^{\prime}=v_{A}(t)} \frac{d v_{A}^{\prime}}{u-v_{A}^{\prime}}=\int_{t^{\prime}=0}^{t^{\prime}=t^{\prime}} \frac{d t^{\prime}}{m_{A, 0}+b t^{\prime}} \nonumber \]
Інтеграція прибутковості
\[\ln \frac{u}{u-v_{A}(t)}=\ln \frac{m_{A, 0}+b t}{m_{A, 0}} \nonumber \]
Знову експоненціюйте обидві сторони, що призведе до
\[\frac{u}{u-v_{A}(t)}=\frac{m_{A, 0}+b t}{m_{A, 0}} \nonumber \]
Після деяких алгебраїчних маніпуляцій ми можемо знайти швидкість автомобіля як функцію часу.
\[v_{A}(t)=\frac{b t}{m_{A, 0}+b t} u \nonumber \]
відповідно до Рівняння (12.3.31).
Результат перевірки:
Ми можемо переписати рівняння (12.3.37) як
\[\left(m_{A, 0}+b t\right) v_{A}(t)=b t u \nonumber \]
що ілюструє момент, що імпульс системи в момент t дорівнює імпульсу зерна, яке було передано системі протягом інтервалу [0, t].
Приклад\(\PageIndex{4}\): Boat and Fire Hose
Палаючий човен маси спочатку\(m_{0}\) знаходиться в стані спокою. Пожежник стоїть на мосту і розпилює воду на човен. Вода виходить з пожежного шланга зі швидкістю u зі швидкістю α (вимірюється в\(\mathrm{kg} \cdot \mathrm{s}^{-1}\)). Припустимо, що рух човна і струменя води горизонтальні, що гравітація не грає ніякої ролі, і що річка може розглядатися як поверхня без тертя. Також припустимо, що зміна маси човна відбувається тільки за рахунок струменя води і що вся вода з струменя додається в човен, (рис. 12.10).

- Через\([t, t+\Delta t]\) часовий проміжок на човен\(\Delta m\) потрапляє кількість води. Вибираємо систему. Чи постійний загальний імпульс у вашій системі? Запишіть диференціальне рівняння, яке є результатом аналізу змін імпульсу всередині вашої системи.
- Інтегруйте диференціальне рівняння, яке ви знайшли в частині a), щоб знайти швидкість v (m) як функцію збільшення маси m човна\(m_{0}\), і u.
Рішення
Візьмемо в якості нашої системи човен, кількість води маси,\(\Delta m_{w}\) яка надходить в човен протягом часового інтервалу\([t, t+\Delta t]\) і яка б вода не була в човні в час t. Вода з пожежного шланга має швидкість u. Позначимо масу човна (включаючи деяку кількість води) в час t по\(m_{b} \equiv m_{b}(t)\), а швидкість човна по\(v \equiv v_{b}(t)\). На\(t+\Delta t\) час швидкість човна є\(v+\Delta v\). Виберіть позитивне х - напрямок в напрямку, в якому рухається човен. Потім х -складові імпульсу системи в момент t і\(t+\Delta t\) показані на малюнку 12.11.

Оскільки ми припускаємо, що палаючий човен ковзає з незначним опором і що гравітація має незначний вплив на дугу струменя води, немає зовнішніх сил, що діють на систему в х -напрямку. Тому х -складова імпульсу системи постійна протягом інтервалу\([t, t+\Delta t]\) і так
\[0=\lim _{\Delta t \rightarrow 0} \frac{p_{x}(t+\Delta t)-p_{x}(t)}{\Delta t} \nonumber \]
Використовуючи інформацію з малюнка вище, Рівняння (12.3.39) стає
\[0=\lim _{\Delta t \rightarrow 0} \frac{\left(m_{b}+\Delta m_{w}\right)(v+\Delta v)-\left(\Delta m_{w} u+m_{b} v\right)}{\Delta t} \nonumber \]
Рівняння (12.3.40) спрощує
\[0=\lim _{\Delta t \rightarrow 0} m_{b} \frac{\Delta v}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} v+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w} \Delta v}{\Delta t}-\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} u \nonumber \]
Третій член зникає, коли ми беремо межу,\(\Delta t \rightarrow 0\) оскільки він другого порядку в нескінченно малих кількостях (у цьому випадку\(\Delta m_{w} \Delta v\)), а коли ділиться\(\Delta t\) на кількість першого порядку і, отже, зникає, оскільки обидва\(\Delta m_{w} \rightarrow 0\) і\(\Delta v \rightarrow 0\) Рівняння (12.3.41) стає
\[0=\lim _{\Delta t \rightarrow 0} m_{b} \frac{\Delta v}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} v-\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} u \nonumber \]
Тепер скористаємося визначенням похідних:
\[\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{d v}{d t} ; \lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t}=\frac{d m_{w}}{d t} \nonumber \]
в Рівнянні (12.3.42) для фінансування диференціального рівняння, що описує зв'язок між прискоренням човна і тимчасовою швидкістю зміни маси води, що надходить в човен
\[0=m_{b} \frac{d v}{d t}+\frac{d m_{w}}{d t}(v-u) \nonumber \]
Маса човна збільшується за рахунок додавання води. Нехай\(m_{w}(t)\) позначають масу води, яка знаходиться в човні в момент t. Тоді масу човна можна записати як
\[m_{b}(t)=m_{0}+m_{w}(t) \nonumber \]
де\(m_{0}\) - маса човна до того, як входила будь-яка вода. Зверніть увагу, ми нехтуємо впливом вогню на масу човна. Диференціююче рівняння (12.3.45) щодо прибутковості часу
\[\frac{d m_{b}}{d t}=\frac{d m_{w}}{d t} \nonumber \]
Тоді рівняння (12.3.44) стає
\[0=m_{b} \frac{d v}{d t}+\frac{d m_{b}}{d t}(v-u) \nonumber \]
(b) Ми можемо інтегрувати це рівняння через поділ змінної техніки. Переписати рівняння (12.3.47) як (скасувати загальний коефіцієнт dt)
\[\frac{d v}{v-u}=-\frac{d m_{b}}{m_{b}} \nonumber \]
Потім ми можемо інтегрувати обидві сторони рівняння (12.3.48) з межами, як показано
\[\int_{v=0}^{v(t)} \frac{d v}{v-u}=-\int_{m_{0}}^{m_{b}(t)} \frac{d m_{b}}{m_{b}} \nonumber \]
Інтеграція прибутковості
\[\ln \left(\frac{v(t)-u}{-u}\right)=-\ln \left(\frac{m_{b}(t)}{m_{0}}\right) \nonumber \]
Нагадаємо, що\(\ln (a / b)=-\ln (b / a)\) так рівняння (12.3.50) стає
\[\ln \left(\frac{v(t)-u}{-u}\right)=\ln \left(\frac{m_{0}}{m_{b}(t)}\right) \nonumber \]
Також нагадаємо, що\(\exp (\ln (a / b))=a / b\) і так експонентірованіе обох сторін рівняння (12.3.51) дає
\[\frac{v(t)-u}{-u}=\frac{m_{0}}{m_{b}(t)} \nonumber \]
Так що швидкість човна в час t може бути виражена як
\[v(t)=u\left(1-\frac{m_{0}}{m_{b}(t)}\right) \nonumber \]
Результат перевірки:
Ми можемо переписати рівняння (12.3.52) як
\[m_{b}(t)(v(t)-u)=-m_{0} u \Rightarrow m_{b}(t) v(t)=\left(m_{b}(t)-m_{0}\right) u \nonumber \]
Нагадаємо, що маса води, яка надходить в автомобіль в проміжку [0, т] дорівнює\(m_{w}(t)=m_{b}(t)-m_{0}\). Тому рівняння (12.3.54) стає
\[m_{b}(t) v(t)=m_{w}(t) u \nonumber \]
Під час взаємодії між струменем води та човном вода передає певну кількість\(m_{w}(t) u\) імпульсу човну та автомобілю, що виробляє імпульс\(m_{b}(t) v(t)\). Оскільки вся вода, яка стикається з човном, опиняється в човні, всі сили взаємодії між струменем води і човном є внутрішніми силами. Човен відкидається вперед і вода відкидається назад і через зіткнення з човном залишається в човні. Тому, якщо ми виберемо в якості нашої системи, всю воду, яка врешті-решт закінчується в човні і човні, то принцип імпульсу стверджує
\[p_{s y s}(t)=p_{s y s}(0) \nonumber \]
де\(p_{s y s}(0)=m_{w}(t) u\) імпульс всієї води, яка в кінцевому підсумку закінчується в човні.
Зверніть увагу, що проблема не просила знайти швидкість човна як функцію t. Зараз ми покажемо, як це знайти. Ми починаємо з того, що спостерігаємо, що
\[\frac{d m_{b}}{d t}=\frac{d m_{w}}{d t} \neq \alpha \nonumber \]
де константа\(\alpha\) вимірюється в\(\mathrm{kg} \cdot \mathrm{s}^{-1}\) і задається як задана константа відповідно до інформації в постановці задачі. Причина полягає в тому\(\alpha\), що швидкість, що вода викидається з шланга, але не швидкість, що вода потрапляє в човен.

Розглянемо невелику кількість води, яка рухається зі швидкістю u, яка в часовому інтервалі Δt протікає через площу поперечного перерізу, орієнтовану перпендикулярно потоку (див. Рис. Площа більше площі поперечного перерізу струменя води. Кількість води, що протікає через елемент площі,\(\Delta m=\lambda u \Delta t\) де λ - це маса на одиницю довжини струменя і\(u \Delta t\) є довжиною струменя, що протікає через площу в інтервалі Δt. Масова норма води, яка протікає через площу поперечного перерізу елемента, тоді
\[\alpha=\frac{\Delta m}{\Delta t}=\lambda u \nonumber \]
На малюнку 12.13 розглянемо невелику довжину\(u \Delta t\) струменя води, яка знаходиться відразу за човном в момент t. За часовий проміжок\([t, t+\Delta t]\) човен рухається на відстань\(v \Delta t\).

Лише частка довжини\(u \Delta t\) води надходить в човен і дається
\[\Delta m_{w}=\lambda(u-v) \Delta t=\frac{\alpha}{u}(u-v) \Delta t \nonumber \]
Рівняння ділення (12.3.59) через\(\Delta t\) і приймаючи межі, ми маємо це
\[\frac{d m_{w}}{d t}=\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t}=\frac{\alpha}{u}(u-v)=\alpha\left(1-\frac{v}{u}\right) \nonumber \]
Заміна рівняння (12.3.53) та рівняння (12.3.46) у рівняння (12.3.60) дає
\[\frac{d m_{b}}{d t}=\alpha\left(1-\frac{v}{u}\right)=\alpha \frac{m_{0}}{m_{b}(t)} \nonumber \]
Ми можемо інтегрувати це рівняння, розділивши змінні, щоб знайти інтегральний вираз для маси човна як функцію часу
\[\int_{m_{0}}^{m_{0}(t)} m_{b} d m_{b}=\alpha m_{0} \int_{t=0}^{t} d t \nonumber \]
Ми можемо легко інтегрувати обидві сторони рівняння (12.3.62)
\[\frac{1}{2}\left(m_{b}(t)^{2}-m_{0}^{2}\right)=\alpha m_{b, 0} t \nonumber \]
Маса човна як функція часу
\[m_{b}(t)=m_{0} \sqrt{1+2 \frac{\alpha t}{m_{0}}} \nonumber \]
Тепер ми замінюємо рівняння (12.3.64) у Рівняння (12.3.65), що дає швидкість палаючого човна як функцію часу
\[v(t)=u\left(1-\frac{1}{\sqrt{1+2 \frac{\alpha t}{m_{b, 0}}}}\right) \nonumber \]
