Пролог
- Page ID
- 76261
Два кардинально різних філософських підходу до науки були розроблені в області класичної механіки протягом 17\(^{th}\) - 18\(^{th}\) століть. Цей часовий період збігся з Епохом Просвітництва в Європі, протягом якого відбувалися чудові інтелектуальні та філософські розробки. Це був час, коли як філософські, так і причинні аргументи були однаково прийнятними в науці, на відміну від нинішньої конвенції, де, як видається, існує мовчазна згода перешкоджати використанню філософських аргументів у науці.
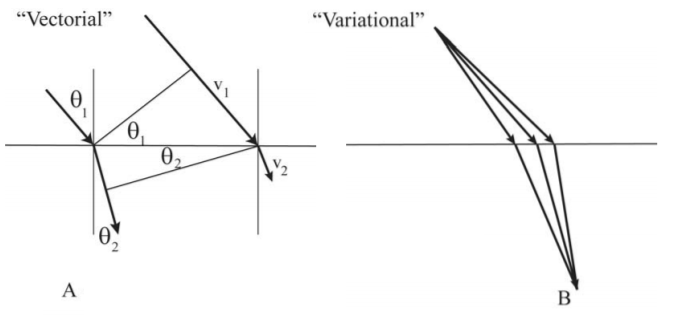
Рисунок F\(\PageIndex{1}\): Векторне та варіаційне зображення закону Снелла для заломлення світла.
Закон Снелла
Генезис двох контрастних філософських підходів до науки відноситься до ранніх досліджень відображення і заломлення світла. Швидкість світла в середовищі показника заломлення\(\textit{n}\) дорівнює\(\mathit{v = \frac{c}{n} }\). Таким чином, світловий промінь, що падає під кутом\( \theta_1 \) до нормалі плоского інтерфейсу між середовищем 1 і середовищем 2, заломлюється під кутом\( \theta_2 \) в середовищі 2, де кути пов'язані законом Снелла.
\ [\ label {EQ:Закон Снелла}\ tag {Закон Снелла}
\ frac {\ sin\ theta_1} {\ sin\ theta_2} =\ розрив {v_1} {v_2} =\ frac {n_2} {n_1}\]
Ібн Сахл з Багдада (984) вперше описав заломлення світла, тоді як Снелл (1621) вивів свій закон математично. Обидва ці вчені використовували «векторний підхід», де швидкість світла\( \mathit{v} \) вважається вектором, що вказує у напрямку поширення.
Принцип Ферма
Принцип найменшого часу Ферма (1657 р.), який заснований на роботі Героя Олександрійського (~ 60) і Ібн аль-Хайтхама (1021), стверджує, що «світло рухається між двома заданими точками по шляху найкоротшого часу», де час транзиту\( \tau \) світлового променя між двома локаціями\(\mathit{A}\) і\(\mathit{B}\) в середовище з залежним від положення показником заломлення,\(\mathit{n(s)}\) заданим
\ [\ tag {Принцип Ферма}
\ tau=\ int_ {T_a} ^ {T_b} dt =\ frac {1} {c}\ int_a^bn (s) ds
\ label {eq:Принцип Фермата}\]
Принцип Ферма призводить до виведення закону Снелла.
Філософськи фізика, що лежить в основі контрастних векторних та принципових висновків Ферма Закону Снелла, різко відрізняється. Векторний підхід заснований на диференціальних співвідношеннях між векторами швидкості в двох середовищах, тоді як варіаційний підхід Ферма заснований на тому, що світло переважно вибирає шлях, для якого інтеграл часу транзиту між початковим\(A\) і кінцевим розташування\(B\) зведено до мінімуму. Тобто перший підхід базується на «векторній механіці», тоді як підхід Ферма базується на варіаційних принципах, оскільки шлях між початковим та кінцевим розташуваннями змінюється, щоб знайти шлях, який мінімізує час транзиту. Проголошення Ферма варіаційних принципів у фізиці зіграло ключову роль в історичному розвитку та подальшій експлуатації принципу найменшої дії в аналітичних формулюваннях класичної механіки, про що йдеться нижче.
Ньютонівська механіка
Імпульс і сила - вектори, які лежать в основі ньютонівської формулювання класичної механіки. Монументальний трактат Ньютона під назвою «Philosopiae Naturalis Principia Mathematica», опублікований у 1687 році, встановив його три універсальні закони руху, універсальну теорію гравітації, виведення трьох законів руху планет Кеплера та розвиток обчислення. Три універсальні закони руху Ньютона забезпечують найбільш інтуїтивний підхід до класичної механіки в тому, що вони засновані на векторних величинях, таких як імпульс, і швидкість зміни імпульсу, які пов'язані з силою. Рівняння руху Ньютона
\[{\bf F} = \frac{d{\bf p}}{dt} \tag{Newton’s equation of motion}\]
являє собою векторне диференціальне співвідношення між миттєвими силами і швидкістю зміни імпульсу, або еквівалентне миттєве прискорення, всі з яких є векторними величинами. Імпульс і силу легко візуалізувати, і причина і наслідок вбудовані в ньютонівську механіку. Таким чином, якщо відомі всі сили, в тому числі і сили обмеження, що діють на систему, то рух можна вирішити для двох систем організму. Математика для обробки підходу Ньютона «векторної механіки» до класичної механіки добре зарекомендувала себе.
Аналітична механіка
Варіаційні принципи застосовуються до багатьох аспектів нашого повсякденного життя. Типові приклади включають; вибір оптимального компромісу за якістю та вартістю при покупці, вибір найшвидшого маршруту для подорожі з дому на роботу або вибір оптимального компромісу для задоволення розрізнених бажань людей, що складають сім'ю. Варіаційні принципи лежать в основі аналітичної формулювання механіки. Дивно, що закони природи узгоджуються з варіаційними принципами, що включають принцип найменшої дії. Мінімізація інтеграла дії призвела до розвитку математичного поля варіаційного числення, плюс аналітичні варіаційні підходи до класичної механіки Ейлера, Лагранжа, Гамільтона та Якобі.
Лейбніц, який був сучасником Ньютона, ввів методи, засновані на величині під назвою «vis viva», яка є латинською мовою «жива сила» і дорівнює вдвічі більшій кінетичній енергії. Лейбніц вірив у філософію, що Бог створив досконалий світ, де природа буде ощадливою у всіх її проявах. У 1707 році Лейбніц запропонував, що оптимальний шлях базується на мінімізації часового інтеграла vis viva, що еквівалентно інтегралу дії лагрангіанської/гамільтонової механіки. У 1744 році Ейлер вивів результат Лейбніца, використовуючи варіаційні концепції, тоді як Мопертюї повторював результат Лейбніца на основі телеологічних аргументів. Розвиток механіки Лагранжа завершився публікацією 1788 року монументального трактату Лагранжа під назвою «Mécanique Analytique». Лагранж використовував принцип д'Аламберта для отримання механіки Лагранжа, що забезпечує потужний аналітичний підхід для визначення величини та напрямку оптимальних траєкторій, плюс пов'язані з ними сили.
Кульмінація розвитку аналітичної механіки відбулася в 1834 році, коли Гамільтон запропонував свій принцип найменшої дії, а також розробку гамільтонової механіки, яка є головним варіаційним підходом в науці. Концепція Гамільтона найменшої дії визначена як часовий інтеграл Лагранжа. Принцип дії Гамільтона (1834) мінімізує інтеграл дії,\(S\) визначені
\[S = \int^B_A L({\bf q}, {\bf \dot{q}}, t ) dt \tag{Hamilton’s Principle}\]
У найпростішому вигляді Лагранж\(L({\bf q}, {\bf \dot{q}}, t )\) дорівнює різниці між кінетичною енергією\(T\) і потенційною енергією\(U\). Принцип найменшої дії Гамільтона лежить в основі механіки Лагранжа. Цей Лагранж є функцією\(n\) узагальнених координат\(q_i\) плюс їх відповідних швидкостей\(\dot{q}_i\). Гамільтон також розробив прем'єр-варіаційний підхід, який називається Гамільтонова механіка, який базується на гамільтоніані,\(H({\bf q}, {\bf p}, t)\) який є функцією\(n\) фундаментального положення\(q_i\) плюс сполучених\(p_i\) змінних імпульсу. У 1843 році Якобі надав математичні рамки, необхідні для повноцінного використання потужності гамільтонової механіки. Зауважимо, що Лагранжа, Гамільтоніана та інтеграла дії - це скалярні величини, що спрощує виведення рівнянь руху порівняно з векторним численням, що використовується ньютонівською механікою.
Рисунок\(\PageIndex{2}\) представляє філософську дорожню карту, що ілюструє ієрархію філософських підходів, заснованих на принципі дії Гамільтона, які доступні для виведення рівнянь руху системи. Первинний\({\bf Stage1}\) використовує функціонал дії Гамільтона,\(S = \int^{t_f}_{t_i} L ({\bf q}, {\bf \dot{q}}, t) dt\) щоб вивести лагранжеві та гамільтонівські функціонали, які забезпечують найбільш фундаментальний та витончений рівень розуміння. \({\bf Stage1}\)передбачає вказівку всіх активних ступенів свободи, а також задіяних взаємодій. \({\bf Stage2}\)використовує функціонал Лагранжа або Гамільтона, похідні при\({\bf Stage1}\), щоб вивести рівняння руху для системи, що цікавить. \({\bf Stage3}\)потім використовує ці похідні рівняння руху для вирішення для руху системи з урахуванням заданої множини початкових граничних умов. Зауважте, що Лагранж вперше похідний лагранжа механіку на основі принципу д'Аламберта, тоді як закони руху Ньютона визначають рівняння руху, що використовуються в ньютонівській механіці.
Аналітичний підхід до класичної механіки виявився суперечливим інтуїтивній векторній обробці Ньютона сили та імпульсу. Існує різка різниця у філософії між векторно-диференціальними рівняннями руху, похідними ньютонівською механікою, які пов'язують миттєву силу з відповідним миттєвим прискоренням, та аналітичною механікою, де мінімізація інтеграла скалярної дії передбачає інтеграли над простором і час між зазначеними початковим і кінцевим станами. Аналітична механіка використовує варіаційні принципи для визначення оптимальної траєкторії з континууму орієнтовних можливостей, вимагаючи, щоб оптимальна траєкторія мінімізувала інтеграл дії між заданими початковими та кінцевими умовами.
Спочатку існувало значне упередження та філософське протиставлення використанню варіаційного принципового підходу, який ґрунтується на припущенні, що природа дотримується принципів економіки. Варіаційний підхід не є інтуїтивним, і тому він вважався спекулятивним і «метафізичним», але він був прийнятий як ефективний інструмент для використання класичної механіки. Це протиставлення варіаційним принципам, що лежать в основі аналітичної механіки, затримувало повне оцінювання варіаційного підходу до початку 20\(^{th}\) століття. Як наслідок, інтуїтивна ньютонівська формулювання панувала в класичній механіці понад два століття, хоча чудові можливості розв'язання проблем аналітичної механіки були визнані та використані після розвитку аналітичної механіки Лагранжем.
Повне значення та переваги аналітичних варіаційних формулювань класичної механіки стали добре визнаними та прийнятими після розробки Спеціальної теорії відносності в 1905 році. Теорія відносності вимагає, щоб закони природи були інваріантними до системи відліку. Це не задовольняє ньютонівська формулювання механіки, яка передбачає одну абсолютну систему відліку і поділ простору і часу. На відміну від цього, Лагранжа і Гамільтонова формулювання принципу найменшої дії залишаються дійсними в теорії відносності, якщо Лагранж написаний в релятивістично-інваріантній формі в просторово-часі. Повна інваріантність варіаційного підходу до координатних кадрів є саме формалізмом, необхідним для обробки релятивістської механіки.
Гамільтонова механіка, яка виражається термінами сполучених змінних\((\mathbf{q}, \mathbf{p})\), відносить класичну механіку безпосередньо до основної фізики квантової механіки і квантової теорії поля. Як наслідок, філософського протистояння використанню варіаційних принципів більше не існує, і гамільтонова механіка стала видатною формулюванням сучасної фізики. Читач вільний робити власні висновки щодо філософського питання «чи є принцип економіки основоположним законом класичної механіки, або це випадковий наслідок фундаментальних законів природи?»
З кінця сімнадцятого століття, аж до зорі сучасної фізики на початку ХХ століття, класична механіка залишалася першочерговою рушійною силою розвитку фізики. Класична механіка охоплює надзвичайно широкий спектр тем, що охоплюють рух макроскопічних астрономічних тіл до мікроскопічних частинок у ядерній фізиці та фізиці частинок, зі швидкостями від нуля до ближньої швидкості світла, від одного тіла до статистичних багатотільних систем, а також мають розширення до квантової механіки. Впровадження спеціальної теорії відносності в 1905 році та загальної теорії відносності в 1916 році зумовило необхідність модифікацій класичної механіки для релятивістських швидкостей і може вважатися розширеною теорією класичної механіки. З 1920-х років квантова фізика витіснила класичну механіку в мікроскопічній області. Хоча квантова фізика відігравала провідну роль у розвитку фізики протягом більшої частини минулого століття, класична механіка все ще є яскравою сферою фізики, яка останнім часом призвела до захоплюючих розробок, пов'язаних з нелінійними системами та теорією хаосу. Це породило нові галузі фізики та математики, а також змінило наше уявлення про причинність.
Цілі
Першочергова мета цієї книги - познайомити читача з потужними варіаційно-принциповими підходами, які відіграють таку ключову роль в класичній механіці та багатьох інших галузях сучасної науки і техніки. Ця книга підкреслює інтелектуальну красу цих чудових подій, а також підкреслює філософські наслідки, які мали величезний вплив на сучасну науку. Другорядною метою є застосування варіаційних принципів для вирішення передових додатків в класичній механіці з метою впровадження багатьох складних і потужних математичних методів, які лежать в основі більшої частини сучасної фізики.
Ця книга починається з огляду ньютонівської механіки плюс розв'язки відповідних рівнянь руху. Далі йде вступ до механіки Лагранжа, заснованої на принципі д'Аламбера, з метою розвитку знайомства у застосуванні варіаційних принципів до класичної механіки. Це призводить до впровадження більш фундаментального принципу дії Гамільтона, плюс Гамільтонова механіка, щоб проілюструвати потужність, що забезпечується використанням повної ієрархії етапів, доступних для застосування варіаційних принципів до класичної механіки. Нарешті книга ілюструє, як варіаційні принципи в класичній механіці використовувалися під час розвитку як релятивізістичної механіки, так і квантової фізики. Зв'язки та застосування класичної механіки до сучасної фізики підкреслюються у всій книзі, намагаючись охопити прірву, яка розділяє ньютонівську векторно-диференціальну формулювання та інтегральну варіаційну формулювання класичної механіки. Ця прірва особливо застосовна до квантової механіки, яка повністю заснована на варіаційних принципах. Відзначимо, що варіаційні принципи, розроблені в області класичної механіки, зараз використовуються в різноманітному і широкому діапазоні областей поза фізикою, включаючи економіку, метеорологію, техніку та обчислювальну техніку.
Це вивчення класичної механіки передбачає сходження на величезну гору знань, а шлях до вершини веде до елегантних і красивих теорій, які лежать в основі більшої частини сучасної фізики. Ця книга використовує варіаційні принципи, застосовані до чотирьох основних тем класичної механіки, щоб проілюструвати силу та важливість варіаційних принципів у фізиці. Будучи настільки близько до саміту, дає можливість зробити кілька додаткових кроків за рамки звичайної вступної класичної механіки навчальної програми, щоб побачити захоплюючу фізику, знайдену на саміті. Ця нова фізика включає такі теми, як квантова, релятивістська та статистична механіка.