10.2: Більше теорії розсіювання - часткові хвилі

Плоскі хвилі і часткові хвилі

Розглядається розв'язання рівняння Шредінгера для розсіювання вхідної плоской хвилі в z -напрямку потенціалом, локалізованим в області поблизу початку, так що сумарна хвильова функція за межами діапазону потенціалу має вигляд\[ \psi(r,\theta,\varphi)= e^{ikr\cos\theta}+f(\theta,\varphi)\frac{e^{ikr}}{r}. \label{10.2.1}\]

Загальна нормалізація не викликає занепокоєння, нас цікавить лише частка вхідної хвилі, яка розсіюється. Очевидно, що вихідний струм, що генерується розсіюванням\(d\Omega\) на твердий кут під\(\theta, \varphi\) кутом,\(|f(\theta,\varphi)|^2d\Omega\) множиться на коефіцієнт швидкості, який також з'являється у вхідній хвилі.

Багато потенціалів в природі сферично симетричні, або майже так, і з точки зору теоретика було б непогано, якби експериментатори могли використовувати цю симетрію, організувавши посилати сферичні хвилі, відповідні різним кутовим моментам, а не порушувати симетрію, вибираючи конкретний напрямок. На жаль, це складно влаштувати, і ми повинні задовольнятися залишилася азимутальною симетрією обертань щодо напрямку вхідного променя.

Насправді, однак, повний аналіз вихідних розсіяних хвиль з вхідної площини хвилі дає таку ж інформацію, як і сферичне розсіювання хвиль. Це пов'язано з тим, що плоска хвиля насправді може бути записана як сума над сферичними хвилями:\[ e^{i\vec{k}\cdot\vec{r}}=e^{ikr\cos\theta}=\sum_l i^l(2l+1)j_l(kr)P_l(\cos\theta) \label{10.2.2}\]

Візуалізуючи цю плоску хвилю, що протікає повз початку, зрозуміло, що в сферичному вираженні плоска хвиля містить як вхідні, так і вихідні сферичні хвилі. Як ми більш детально обговоримо на наступних кількох сторінках, реальна функція\(j_l(kr)\) - це стояча хвиля, що складається з вхідних і вихідних хвиль однакової амплітуди.

Нас, очевидно, цікавлять лише вихідні сферичні хвилі, які походять від розсіювання від потенціалу, тому ми повинні бути обережними, щоб не сплутати вже існуючі вихідні хвильові компоненти плоской хвилі з новими вихідними хвилями, породженими потенціалом.

Радіальні функції,\(j_l(kr)\) що виникають у вищезгаданому розширенні плоской хвилі в її сферичних компонентах, є сферичними функціями Бесселя, розглянутими нижче. Азимутальна обертальна симетрія плоской хвилі+сферичного потенціалу навколо напрямку вхідної хвилі гарантує, що кутова залежність хвильової функції справедлива\(P_l(\cos\theta)\), а не\(Y_{lm}(\theta,\varphi)\). Коефіцієнт\(i^l(2l+1)\) виводиться в Ландау і Ліфшиці,\(\S\) 34, шляхом порівняння коефіцієнта з двох сторін рівняння: як ми побачимо нижче,\((kr)^n\) не відображається в\(j_l(kr)\)\(l\) більше\(n\), ніж і\((\cos\theta)^n\) не відображається в\((kr\cos\theta)^n\)\(P_l(\cos\theta)\) для\(l\) менше\(n\), тому комбінація відбувається\((kr\cos\theta)^n\) лише один раз - у\(n^{th}\) термін, і коефіцієнти з обох сторін рівняння можуть бути узгоджені. (Щоб отримати правильний коефіцієнт, ми повинні, звичайно, вказати нормалізації для функції Бесселя - див. Нижче - і полінома Лежандра.)

Математичний інтервал: сферичні функції Бесселя та Неймана

Плоска хвиля\(e^{i\vec{k}\cdot\vec{r}}\) є тривіальним розв'язком рівняння Шредінгера з нульовим потенціалом, і тому, оскільки\(P_l(\cos\theta)\) утворюють лінійно незалежну множину, кожен член\(j_l(kr)P_l(\cos\theta)\) плоского хвильового ряду повинен сам бути розв'язком рівняння Шредінгера з нульовим потенціалом. Звідси випливає, що\(j_l(kr)\) задовольняє радіальне рівняння Шредінгера з нульовим потенціалом:\[ \frac{d^2}{dr^2}R_l(r)+\frac{2}{r}\frac{d}{dr}R_l(r)+\left( k^2-\frac{l(l+1)}{r^2}\right) R_l(r)=0. \label{10.2.3}\]

Стандартна заміщення\(R_l(r)=u_l(r)/r\) прибутковості\[ \frac{d^2u_l(r)}{dr^2}+\left( k^2-\frac{l(l+1)}{r^2}\right)u(r)=0 \label{10.2.4}\]

Для простого випадку двома\(l=0\) розв'язками є\(u_0(r)=\sin kr,  \cos kr.\) відповідні\(R_0(r)\) радіальні функції (крім загальних констант) функції Бесселя та Неймана нульового порядку відповідно.

Стандартна нормалізація для функції Бесселя нульового порядку дорівнює\[ j_0(kr)=\frac{\sin kr}{kr}, \label{10.2.5}\]

і функція Неймана нульового порядку\[ n_0(kr)=-\frac{\cos kr}{kr}. \label{10.2.6}\]

Зауважте, що функція Бесселя є тією, яка добре поводиться на початку: вона може бути згенерована шляхом інтеграції з початковими граничними умовами значення один, нахил нуль.

Ось сюжет\(j_0(kr)\) і\(n_0(kr)\) від\(kr=0.1\; to\; 20\):

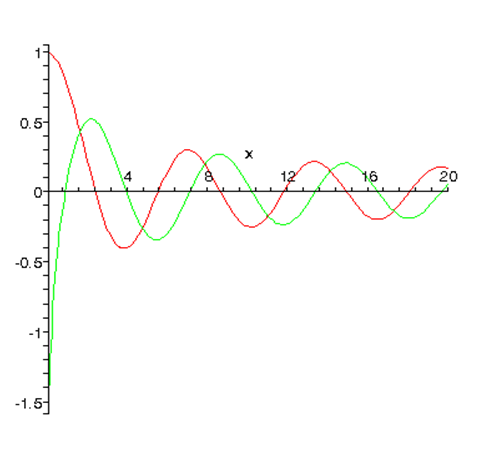
Для ненульових\(l\), поблизу походження\(R_l(r)\sim r^l\) або\(\sim r^{-(l+1)}\). Добре поведене\(\sim r^l\) рішення - функція Бесселя, сингулярна функція - функція Неймана. Стандартні нормалізації цих функцій наведені нижче.

Ось\(j_5(kr)\) і\(j_{50}(kr)\):

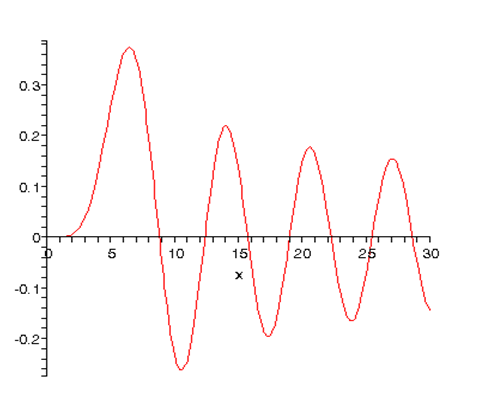
Детальне виведення функцій Бесселя та Неймана

Цей підрозділ якраз тут для повноти. Використовуємо безрозмірну змінну\(\rho=kr\).

Щоб знайти вищі\(l\) рішення, ми дотримуємося розумного трюку, наведеного в Ландау та Ліфшиці (\(\S\)33).

Фактор\(\rho^l\) поведінки поблизу походження шляхом написання\[ R_l=(\rho)^l\chi_l(\rho). \label{10.2.7}\]

Функція\(\chi_l(\rho)\) задовольняє\[ \frac{d^2}{d\rho^2}\chi_l(\rho)+\frac{2(l+1)}{\rho}\frac{d}{d\rho}\chi_l(\rho)+\chi_l(\rho)=0. \label{10.2.8}\]

Хитрість полягає в тому, щоб диференціювати це рівняння щодо\(\rho\):\[ \frac{d^3}{d\rho^3}\chi_l(\rho)+\frac{2(l+1)}{\rho}\frac{d^2}{d\rho^2}\chi_l(\rho)+\left( 1-\frac{2(l+1)}{\rho^2}\right)\frac{d}{d\rho}\chi_l(\rho)=0. \label{10.2.9}\]

Пишучи чисто формально\(\frac{d}{d\rho}\chi_l(\rho)=\rho\chi_{l+1}(\rho)\), рівняння стає\[ \frac{d^2}{d\rho^2}\chi_{l+1}(\rho)+\frac{2(l+2)}{\rho}\frac{d}{d\rho}\chi_{l+1}(\rho)+\chi_{l+1}(\rho)=0. \label{10.2.10}\]

Але це рівняння, яке\(\chi_{l+1}(\rho)\) повинно підкорятися! Таким чином, у нас є формула рекурсії для генерації всіх\(j_l(\rho)\) від нульового:\(\chi_{l+1}(\rho)=\frac{1}{\rho}\frac{d}{d\rho}\chi_l(\rho)\), і, аж до нормалізації константи\(j_l(\rho)=(\rho)^l\chi_l(\rho)\), закріпленої за умовністю.

По суті, стандартна нормалізація\[ j_l(\rho)=(-\rho)^l\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\left(\frac{\sin\rho}{\rho}\right). \label{10.2.11}\]

Зараз\[ (\sin\rho)/\rho=\sum_0^{\infty} (-1)^n\rho^{2n}/(2n+1)! \label{10.2.12}\]

Це сума тільки парних повноважень\(\rho\). Легко перевірити, що робота на цій серії з ніколи не\(\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\) може генерувати будь-яких негативних сил\(\rho\). Звідси випливає\(j_l(\rho)\), що, написаний як силовий ряд в\(\rho\), має провідний термін пропорційний\(\rho^l\). Коефіцієнт цього провідного члена можна знайти, застосувавши диференціальний оператор до ряду для\((\sin\rho)/\rho\),\[ j_l(\rho)\sim \frac{\rho^l}{(2l+1)!!} \; as \; \rho\to0. \label{10.2.13}\]

Така\(r^l\) поведінка поблизу походження є звичайним добре поведеним рішенням рівняння Шредінгера в регіоні, де домінує відцентровий термін.

Зверніть увагу, що невелика\(\rho\) поведінка не відразу видно зі звичайного представлення тих\(j_l(\rho)\), написаних як суміш повноважень і тригонометричних функцій, наприклад\[ j_1(\rho)=\frac{\sin\rho}{\rho^2}-\frac{\cos\rho}{\rho},\;\; j_2(\rho)=\left( \frac{3}{\rho^3}-\frac{1}{\rho}\right)\sin\rho-\frac{3\cos\rho}{\rho^2}, \; etc. \label{10.2.14}\]

Звертаючись тепер до поведінки для великих\(\rho\), від\(j_l(\rho)\)\[ j_l(\rho)=(-\rho)^l\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\left(\frac{\sin\rho}{\rho}\right) \label{10.2.15}\]

очевидно, що домінантний термін у великому\(\rho\) режимі (порядку\(1/\rho\)) породжується диференціацією лише тригонометричної функції на кожному кроці. Кожна така диференціація може бути еквівалентною множенню на (-1) та відніманню\(\pi /2\) з аргументу, тому\[ j_l(\rho)\to \frac{1}{\rho}\sin\left(\rho-\frac{l\pi}{2}\right) \; as\; \rho\to\infty . \label{10.2.16}\]

Це\(j_l(\rho)\), отже, фізичні частково-хвильові розв'язки рівняння Шредінгера з нульовим потенціалом. Коли потенціал увімкнений, хвильова функція біля початку все ще залишається\(\sim \rho^l\) (припускаючи, як ми завжди робимо, що потенціал незначний порівняно з\(l(l+1)/\rho^2\) терміном, досить близьким до походження). Хвильова функція за межами діапазону потенціалу може бути знайдена чисельно в принципі шляхом інтеграції з походження, і насправді буде як\(j_l(\rho)\) вище, за винятком того, що буде додатковий фазовий фактор, званий «фазовим зсувом» і позначається\(\delta\)) в синусі. Значення цього полягає в тому, що в далекій області хвильова функція являє собою лінійну комбінацію функції Бесселя і функції Неймана (розв'язання сингулярного рівняння Шредінгера з нульовим потенціалом у початку). Тому необхідно також переглянути функції Неймана.

Як було сказано вище, функція\(l=0\) Неймана є\[ n_0(\rho)=-\frac{\cos\rho}{\rho}, \label{10.2.17}\]

знак мінус є стандартною конвенцією.

Аргумент, паралельний описаному вище для функцій Бесселя, встановлює, що функції Неймана вищого порядку задаються:\[ n_l(\rho)=(-\rho)^l\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\left(-\frac{\cos\rho}{\rho}\right). \label{10.2.18}\]

Поруч з походженням\[ n_l(\rho)\sim \frac{(2l-1)!!}{\rho^{l+1}} \; as\; \rho\to0 \label{10.2.19}\]

і для великих\(\rho\)\[ n_l(\rho)\to -\frac{1}{\rho}\cos\left(\rho-\frac{l\pi}{2}\right)\; as\; \rho\to\infty , \label{10.2.20}\]

тож функція форми\(\frac{1}{\rho}\sin\left(\rho-\frac{l\pi}{2}+\delta\right)\) асимптотично може бути записана як лінійна комбінація функцій Бесселя та Неймана в цій області.

Нарешті, сферичні функції Ханкеля - це лише комбінації функцій Бесселя та Неймана, які виглядають як вихідні або вхідні плоскі хвилі в асимптотичній області:\[ h_l(\rho)=j_l(\rho)+in_l(\rho),\;\; h_l^*(\rho)=j_l(\rho)-in_l(\rho), \label{10.2.21}\]

так для великих\(\rho\),\[ h_l(\rho)\to \frac{e^{i(\rho-l\pi /2)}}{i\rho},\;\; h_l^*(\rho)\to -\frac{e^{-i(\rho-l\pi /2)}}{i\rho}. \label{10.2.22}\]

Матриця часткового розсіювання хвиль

Уявімо на мить, що ми могли б просто послати (незалежну від часу) сферичну хвилю, з\ theta варіацією, заданою\(P_l(\cos\theta)\). Для цієї\(l^{th}\) часткової хвилі (скидання загальних констант нормалізації, як зазвичай) радіальна функція, далека від початку нульового потенціалу, дорівнює\[ j_l(kr)\to \frac{1}{kr}\sin\left(kr-\frac{l\pi}{2}\right)=\frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{+i(kr-l\pi /2)}}{r}\right). \label{10.2.23}\]

Якщо зараз включений (сферично симетричний) потенціал, єдиною можливою зміною цього стоячого хвильового рішення в далекій області (де потенціал дорівнює нулю) є зсув фази\(\delta\):\[ \sin\left(kr-\frac{l\pi}{2}\right)\to \sin\left(kr-\frac{l\pi}{2}+\delta_l(k)\right). \label{10.2.24}\]

Це те, що ми знайшли б при інтеграції рівняння Шредінгера з несингулярної поведінки на початку.

Але на практиці дається вхідна хвиля, і на її фазу неможливо вплинути включенням потенціалу. Але ми все ще повинні мати рішення того ж рівняння Шредінгера, тому, щоб збігатися з результатом вище, ми помножимо всю частинну хвильову функцію на фазовий коефіцієнт\(e^{i\delta_l(k)}\). Результат полягає в тому, щоб поставити подвійну зміну фази на вихідну хвилю, так що при включенні потенціалу зміна асимптотичної хвильової функції повинна бути\[ \frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{+i(kr-l\pi /2)}}{r}\right)\to \frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{S_l(k)e^{+i(kr-l\pi /2)}}{r}\right). \label{10.2.25}\]

Це рівняння вводить матрицю розсіювання\[ S_l(k)=e^{2i\delta_l(k)}, \label{10.2.26}\]

який повинен лежати на\(|S|=1\) одиничному колі, щоб зберегти ймовірність - вихідний струм повинен дорівнювати вхідному струму. Якщо розсіювання немає, тобто зсуву фаз нуля, матриця розсіювання дорівнює одиниці.

Слід зазначити, що коли радіальне рівняння Шредінгера розв'язується для ненульового потенціалу шляхом інтеграції з початку, причому\(\psi=0\) і\(\psi′=1\) спочатку реальна функція, створена таким чином, відрізняється від хвильової функції, наведеної вище загальним фазовим коефіцієнтом\(e^{i\delta_l(k)}\).

Розсіювання плоскої хвилі

Тепер ми готові взяти вхідну площину хвилі, розбити її на її часткові хвильові компоненти, відповідні різним кутовим моментам, мати часткові хвилі індивідуально фази, зсунуті на\(l\) - залежні фази, і додати все це разом, щоб отримати вихідну площину хвилі плюс розсіяну хвилю.

Нас цікавить лише хвильова функція далеко від потенціалу. У цьому регіоні початкова плоска хвиля\[ \begin{matrix} e^{i\vec{k}\cdot\vec{r}}=e^{ikr\cos\theta}=\sum_l i^l(2l+1)j_l(kr)P_l(\cos\theta) \\ =\sum_l i^l(2l+1)\frac{i}{2k}(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{+i(kr-l\pi /2)}}{r})P_l(\cos\theta). \end{matrix}\label{10.2.27}\]

Включення потенційних фазових зсувів коефіцієнта вихідної хвилі:\[ \frac{e^{+i(kr-l\pi /2)}}{r}\to \frac{S_l(k)e^{+i(kr-l\pi /2)}}{r} \label{10.2.28}\]

Фактичне розсіювання потенціалом - це різниця між цими двома членами. Повна хвильова функція в далекій області (включаючи вхідну площину хвилі), таким чином:\[ \psi(r,\theta,\varphi)=e^{ikr\cos\theta}+\left(\sum_l(2l+1)\frac{(S_l(k)-1)}{2ik}P_l(\cos\theta)\right)\frac{e^{ikr}}{r}. \label{10.2.29}\]

\(i^l\)Фактор скасував\(e^{-il\pi /2}\). -1 in\((S_l(k)-1)\) є, тому що нуль розсіювання означає\(S=1\). Крім того, це можна розглядати як віднімання вихідних хвиль, вже присутніх у площинній хвилі, як обговорювалося вище. Немає\(\varphi\) - залежності, оскільки при сферично-симетричному потенціалі вся задача азимутально симетрична щодо напрямку вхідної хвилі.

Можливо, варто згадати, що для розсіювання всього в одній частковій хвилі вихідний струм дорівнює вхідному струму, чи є зсув фаз чи ні. Отже, якщо включення потенціалу не впливає на загальний струм, розсіяний в будь-якій частковій хвилі, то як це може викликати будь-яке розсіювання? Справа в тому, що для вхідної площини хвилі з нульовим потенціалом вхідні та вихідні компоненти мають правильну відносну фазу для додавання до компонента плоської хвилі - можливо, тавтологія. Але якщо додаткову фазу вводять лише у вихідну хвилю, вхідний + вихідний більше не дасть плоску хвилю - буде додаткова вихідна частина, пропорційна\((S_l(k)-1)\).

Нагадаємо, що амплітуда розсіяння\(f(\theta,\varphi)\) була визначена в терміні розв'язку рівняння Шредінгера, що має вхідну плоску хвилю,\[ \psi(r,\theta,\varphi)=e^{ikr\cos\theta}+f(\theta,\varphi)\frac{e^{ikr}}{r}. \label{10.2.30}\]

Тепер ми готові висловити амплітуду розсіювання через часткові хвильові фазові зсуви (звичайно, для сферично симетричного потенціалу):\[ f(\theta,\varphi)=f(\theta)=\sum_l(2l+1)\frac{(S_l(k)-1)}{2ik} P_l(\cos\theta)=\sum_l(2l+1)f_l(k)P_l(\cos\theta) \label{10.2.31}\]

де\[ f_l(k)=\frac{1}{k}e^{i\delta_l(k)}\sin\delta_l(k) \label{10.2.32}\]

називається частковою амплітудою розсіювання хвиль або просто частковою амплітудою хвилі.

Отже, загальна амплітуда розсіяння є сумою цих часткових амплітуд хвиль:\[ f(\theta)=\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta). \label{10.2.33}\]

Загальний переріз розсіювання\[ \begin{matrix} \sigma =\int |f(\theta)|^2d\Omega \\ =2\pi \int_0^{\pi} |f(\theta)|^2\sin\theta d\theta \\ =2\pi \int_0^{\pi}  |\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta)|^2​\sin\theta d\theta \end{matrix} \label{10.2.34}\]

дає\[ \sigma =4\pi \sum_{l=0}^{\infty} (2l+1)|f_l(k)|^2=\frac{4\pi}{k^2}\sum_{l=0}^{\infty} (2l+1)\sin^2\delta_l.\label{10.2.35}\]

Отже, загальний перетин - це сума перетинів для кожної\(l\) величини. Однак це не означає, що диференціальний переріз для розсіювання на заданий твердий кут є сумою над окремими\(l\) значеннями - різні компоненти заважають. Тільки тоді, коли всі кути інтегровані над, ортогональність многочленів Лежандра гарантує, що перехресні члени зникнуть.

Зверніть увагу, що максимально можливий поперечний переріз розсіювання для частинок у стані моменту імпульсу\(l\) є\((4\pi /k^2)(2l+1)\), що в чотири рази більше класичного перерізу для цієї часткової хвилі, що впливає, скажімо, на тверду сферу! (Уявіть собі напівкласично частинки в кільцевій області: кутовий момент моменту\(L=rp\), скажімо, але\(L=\hbar l\) і\(p=\hbar k\) так\(l=rk\). Тому кільцева область, що відповідає кутовому моменту «між»\(l\) і\(l+1\) має внутрішній і зовнішній радіуси\(l/k\)\((l+1)/k\) і, отже, площа\(\pi (2l+1)/k^2\).) Квантовий результат по суті є дифракційним ефектом, ми обговоримо його пізніше.

Довести оптичну теорему для сферично-симетричного потенціалу легко: просто візьміть уявну частину кожної сторони рівняння\[ f(\theta)=\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta) \label{10.2.36}\]

в\(\theta=0\), використовуючи\(P_l(1)=1\),\[ Im\, f(\theta=0)=\frac{1}{k}\sum_l(2l+1)\sin^2\delta_l(k) \label{10.2.37}\]

з якого відразу\(Im\, f(0)=k\sigma /4\pi\) випливає оптична теорема.

Варто також відзначити, що має на\(S_l^{\dagger}S_l=1\) увазі унітарність матриці\(l^{th}\) часткового розсіювання хвиль для часткової амплітуди хвилі\(f_l(k)=\frac{1}{k}e^{i\delta_l(k)}\sin\delta_l(k)\). Так як\(S_l(k)=e^{2i\delta_l(k)}\), випливає, що\[ S_l(k)=1+2ikf_l(k). \label{10.2.38}\]

З цього\(S_l^{\dagger}S_l=1\) дає:\[ Im\, f_l(k)=k|f_l(k)|^2. \label{10.2.39}\]

Це можна сказати простіше:\[Im\, \frac{1}{f_l(k)}=-k. \label{10.2.40}\]

Фактично,\[ f_l(k)=\frac{1}{k(\cot\delta_l(k)-i)}. \label{10.2.41}\]

Фазові зрушення та потенціали: деякі приклади

У цьому розділі ми припускаємо, що потенціал може бути прийнятий рівним нулю за деяким граничним радіусом\(b\). Це адекватне наближення для всіх знайдених на практиці потенціалів, крім кулонівського потенціалу, про який і піде мова окремо далі.

Асимптотично, значить,\[ \begin{matrix} \psi_l(r)=\frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{2i\delta_l(k)}e^{+i(kr-l\pi /2)}}{r}\right) \\ =\frac{e^{i\delta_l(k)}}{kr}\sin(kr+\delta_l(k)-l\pi /2) \\ =\frac{e^{i\delta_l(k)}}{kr}(\sin(kr-l\pi /2)\cos\delta_l(k)+\cos(kr-l\pi /2)\sin\delta_l(k)). \end{matrix} \label{10.2.42}\]

Цей вираз точно тільки в межі\(r\to \infty\), але так як потенціал можна прийняти за нуль далі\(r=b\), хвильова функція повинна мати вигляд\[ \psi_l(r)=e^{i\delta_l(k)}(\cos\delta_l(k)j_l(kr)-\sin\delta_l(k)n_l(kr)) \label{10.2.43}\]

для\(r>b\).

(Знак - походить від стандартної конвенції для функцій Бесселя і Неймана - див. Раніше.)

Жорстка сфера

Найпростіший приклад потенціалу розсіювання:\[ \begin{matrix} V(r)=\infty \; for\; r<R, \\ V(r)=0\; for\; r\ge R. \end{matrix}\label{10.2.44}\]

Хвильова функція повинна дорівнювати нулю при\(r=R\), тому з наведеної вище форми\(\psi_l(r)\),\[ \tan\delta_l(k)=\frac{j_l(kR)}{n_l(kR)} .\label{10.2.45}\]

Для\(l=0\),\[ \tan\delta_0(k)=-\frac{(\sin kR)/kR}{(\cos kR)/kR}=-\tan kR, \label{10.2.46}\]

так\(\delta_0(k)=-kR\). Це означає, що хвильова функція ефективно переміщається, щоб почати з,\(R\) а не на початку:\[ \frac{\sin kr}{kr}\to \frac{\sin k(r+\delta)}{kr}=\frac{\sin k(r-R)}{kr} \label{10.2.47}\]

для\(r>R\), звичайно,\(\psi=0\) для\(r<R\).

Для більш високих станів моменту моменту при низьких енергіях\(( kR\ll 1 )\),\[ \tan\delta_l(k)=\frac{j_l(kR)}{n_l(kR)}\approx \frac{-(kR)^l/(2l+1)!!}{(2l-1)!!/(kR)^{l+1}}=-\frac{(kR)^{2l+1}}{(2l+1)((2l-1)!!)^2}. \label{10.2.48}\]

Тому при досить низькій енергії важливо лише\(l=0\) розсіювання - як це очевидно, оскільки вхідна частка з імпульсом\(p=\hbar k\) і кутом імпульсу, швидше за все,\(l\hbar\) знаходиться на відстані\(l/k\) від центру потенціалу при найближчому наближенні, тому якщо це набагато більше\(R\), ніж, зсув фаз буде невеликим.

Народжене наближення для часткових хвиль

З визначення\(f(\theta,\varphi)\)\[ \psi_{\vec{k}}(\vec{r})=e^{i \vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{ikr}}{r} \label{10.2.49}\]

і\[ \psi_{\vec{k}}(\vec{r})=e^{i \vec{k}\cdot\vec{r}}-\frac{m}{2\pi \hbar^2}\frac{e^{ikr}}{r}\int d^3 r'e^{-i \vec{k}_f\cdot\vec{r}'}V(\vec{r}') \psi_{\vec{k}}(\vec{r}') \label{10.2.50}\]

нагадати наближення Борна становить заміну хвильової функції\(\psi_{\vec{k}}(\vec{r}')\) в інтегралі праворуч на вхідну плоску хвилю, тому ігноруючи розсіювання.

Щоб перевести це в часткове хвильове наближення, ми спочатку приймаємо вхідний бути\(\vec{k}\) в напрямку z-, тому в integrand ми\(\psi_{\vec{k}}(\vec{r}')\) замінюємо на\[ e^{ikr'\cos\theta}=\sum_l i^l(2l+1)j_l(kr')P_l(\cos\theta'). \label{10.2.51}\]

Маркування кута між\(\vec{k}_f\) і\(\vec{r}'\) по\(\gamma\),\[ e^{-i \vec{k}_f\cdot\vec{r}'}=\sum_l(-i)^l(2l+1)j_l(kr')P_l(\cos\gamma). \label{10.2.52}\]

Тепер \(\vec{k}_f\)знаходиться в напрямку\((\theta,\varphi)\) і\(\vec{r}'\) в напрямку\((\theta',\varphi')\), і\(\gamma\) є кут між ними. Для цієї ситуації існує теорема додавання сферичних гармонік:\[ P_l(\cos\gamma)=\frac{4\pi}{2l+1}\sum_{m=-l}^{l} Y^∗_{lm}(\theta',\varphi')Y_{lm}(\theta,\varphi). \label{10.2.53}\]

Вставляючи цей вираз та інтегруючи над\(\theta',\varphi'\), ненульові\(m\) члени дають нуль, насправді єдиним ненульовим терміном є те, що з\(l\) таким же терміном у\(\psi_{\vec{k}}(\vec{r}')\) розширенні, даючи\[ f(\theta)=\frac{-2m}{\hbar^2}\sum_{l=0}^{\infty} (2l+1)P_l(\cos\theta)\int_0^{\infty} r^2drV(r)(j_l(kr))^2 \label{10.2.54}\]

і запам'ятовування\[ f(\theta)=\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta) \label{10.2.55}\]

випливає, що для малих фазових зсувів (єдине місце, яке воно дійсне) частково-хвильова наближення Born читає\[ \delta_l(k)\approx -\frac{2mk}{\hbar^2}\int_0^{\infty} r^2drV(r)(j_l(kr))^2. \label{10.2.56}\]

Низька енергія розсіювання: довжина розсіювання

Від

\[ f_l(k)=\frac{1}{k(\cot\delta_l(k)-i)}, \label{10.2.41B}\]

\(l=0\)перетин становить

\[ \sigma_{l=0}=\frac{4\pi}{k^2|\cot\delta_0(k)-i|^2}. \label{10.2.57}\]

При енергії\(E\to0\) радіальне рівняння\(u=r\psi\) Шредінгера для віддалення від потенціалу стає\(d^2u/dr^2=0\) з прямим розв'язком\(u(r)=C(r-a)\). Це повинна бути\(k\to 0\) межа\(u(r)=C′\sin(kr+\delta_0(k))\), яка може бути правильною тільки в тому випадку, якщо\(\delta_0\) вона сама\(k\) лінійна в для досить малих\(k\), і тоді вона повинна бути\(\delta_0(k)=-ka\), будучи точкою, в якій екстрапольована зовнішня хвильова функція перетинає вісь (можливо, при негативній\(r\)!) Отже, як\(k\) йде до нуля, термін ліжечка домінує в знаменнику і\[ \sigma_{l=0}(k\to 0)=4\pi a^2.\label{10.2.58}\]

Величина a називається довжиною розсіювання.

Інтегруючи радіальне рівняння Шредінгера з нульовою енергією від\(u(r)=0\) початку для слабкого (сферичного) квадратного потенціалу ями, легко перевірити, що a є позитивним для потенціалу\(a\) відштовхування, негативним для привабливого потенціалу.

Відштовхуючий потенціал, хвильова функція нульової енергії (так що це пряма лінія поза свердловиною!) :

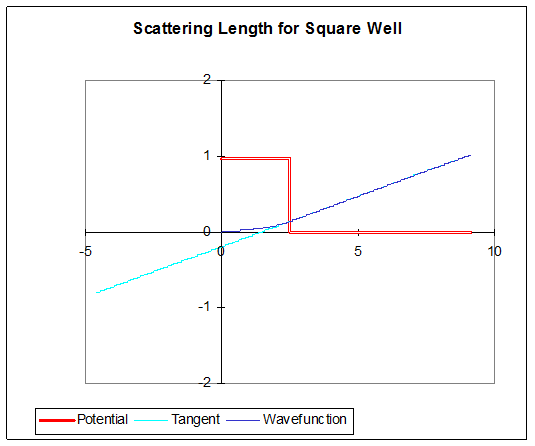
Привабливий потенціал:

При збільшенні сили потенціалу відштовхування, все ще вирішуючи для хвильової функції нульової енергії,\(a\) прагне до потенційної стінки - ось хвильова функція нульової енергії для бар'єру висотою 6:

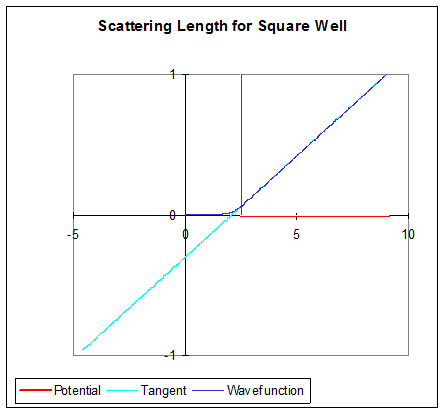
Для нескінченно високого бар'єру хвильова функція виштовхується з бар'єру повністю, і результат жорсткої сфери відновлюється: довжина розсіювання\(a\), поперечний переріз\(4\pi a^2\).

При збільшенні міцності привабливого колодязя, якщо буде зміна фази більше, ніж\(\pi /2\) всередині свердловини,\(a\) стане позитивним. Насправді, прямо на\(\pi /2\),\(a\) нескінченно!

А ще трохи глибини колодязю дає позитивна довжина розсіювання:

Насправді, добре досить глибоко, щоб мати позитивну довжину розсіювання, також матиме пов'язаний стан. Це стає очевидним, коли вважають, що глибину, на якій довжина розсіювання стає нескінченною, можна вважати формально пов'язаним з нульовою енергією стан, в тому, що, хоча хвильова функція зовні не нормалізується, вона еквівалентна експоненціально гниючої функції з нескінченною довжиною розпаду. Якщо зараз трохи поглиблювати свердловину, хвильова функція нульової енергії всередині свердловини вигинається трохи швидше, тому нахил хвильової функції на краю свердловини стає негативним, як на малюнку вище. За допомогою цього трохи глибшого колодязя тепер ми можемо трохи знизити енергію до негативних значень. Це мало вплине на хвильову функцію всередині свердловини, але зробить можливим прилягання на краю свердловини до експоненціального розпаду зовні - справжнього пов'язаного стану, з хвильовою функцією\(\sim e^{-\kappa r}\) поза свердловиною.

Якщо енергія зв'язку стану дійсно низька, хвильова функція розсіювання нульової енергії всередині свердловини практично ідентична цій дуже низькій енергетичній зв'язаному стані, і, зокрема, логарифмічна похідна біля стінки буде дуже близько, тому\(\kappa \cong 1/a\), приймаючи\(a\) бути набагато більше, ніж радіус свердловини.

Це пов'язує велику довжину розсіювання з енергією слабозв'язаного стану,\[ B. E. =\hbar^2k^2/2m=\hbar^2/2ma^2. \label{10.2.59}\]

Вігнер першим використав це для оцінки енергії зв'язку дейтрона від спостережуваного поперечного перерізу для низькоенергетичного нейтрон-протонного розсіяння.