10.1: Теорія розсіювання

Майже все, що ми знаємо про ядра та елементарні частинки, було виявлено в експериментах з розсіювання, від подиву Резерфорда, виявивши, що атоми мають свою масу та позитивний заряд зосереджені в майже точкових ядрах, до більш пізніх відкриттів, на набагато меншій шкалі довжини, що протони а нейтрони самі складаються з явно точкових кварків.

Найпростіша модель експерименту з розсіянням наведена шляхом розв'язання рівняння Шредінгера для плоскої хвилі, що впливає на локалізований потенціал. Потенціал\(V(r)\) може представляти те, з чим стикається швидкий електрон при ударі атома, або альфа-частинки ядра. Очевидно, що представляти будь-яку таку систему потенціалом - це лише початок, але в певних енергетичних діапазонах це цілком розумно, і ми повинні з чогось починати!

Основний сценарій полягає в тому, щоб стріляти в потоці частинок, все з однаковою енергією, і виявити, скільки відхилено в батарею детекторів, які вимірюють кути відхилення. Ми припускаємо, що всі вхідні частинки представлені хвильовими пакетами однакової форми та розміру, тому слід вирішити залежне від часу рівняння Шредінгера для такого хвильового пакета і знайти амплітуди ймовірностей для вихідних хвиль в різних напрямках через деякий час після того, як відбулося розсіювання. Але ми застосовуємо простіший підхід: ми припускаємо, що хвильовий пакет має чітко визначену енергію (а отже, і імпульс), тому він має багато довжин хвиль. Це означає, що під час процесу розсіювання він багато в чому схожий на плоску хвилю, і протягом певного періоду часу розсіювання є незалежним від часу. Тоді ми припускаємо, що задача добре апроксимується шляхом розв'язання незалежного від часу рівняння Шредінгера з вхідною плоскою хвилею. Це набагато простіше!

Все, що ми можемо виявити, - це вихідні хвилі далеко за межами області розсіювання. Для вхідної плоской хвилі\(e^{i\vec{k}\cdot\vec{r}}\) хвильова функція далеко від області розсіювання повинна мати вигляд\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{i k r}}{r} \label{10.1.1}\]

де\(\theta,\varphi\) вимірюються щодо вхідного напрямку.

Зверніть увагу, що амплітуда розсіювання\(f(\theta,\varphi)\) має розміри довжини.

Ми не турбуємося про загальну нормалізацію, тому що актуальною є частка вхідного променя, розсіяного в певному напрямку, або, якщо бути точніше, на невеликий суцільний кут\(d\Omega\) у напрямку\(\theta,\varphi\). Вхідний струм частинок (з вищевказаною нормалізацією) проходить\(\hbar k/m=v\) через одиницю площі, перпендикулярну вхідному пучку, вихідний струм в\(d\Omega\) малий кут\((\hbar k/m)|f(\theta,\varphi)|^2d\Omega\). Очевидно, що цей вихідний струм відповідає вихідному вхідному струму, що протікає через перпендикулярну площу розміру\(d\sigma(\theta,\varphi)=|f(\theta,\varphi)|^2d\Omega\), і\[ \frac{d\sigma}{d\Omega}=|f(\theta,\varphi)|^2 \label{10.1.2}\]

називається диференціальним перетином для розсіювання в напрямку\( \theta,\varphi\).

Незалежний від часу опис

Ми розглянемо незалежну від часу формулювання теорії розсіяння, спочатку, як вона представлена в Баймі, з точки зору стандартних хвильових функцій рівняння Шредінгера, потім зробити те ж саме a la Sakurai, в більш формальному, але, звичайно, еквівалентному, мова бюстгальтерів і кетів. Підхід до хвильової функції Шредінгера є більш простим введенням, але формальна мова більш зручна для аналізу структури термінів вищого порядку.

Насправді, лікування Байма не зовсім незалежне від часу, оскільки він використовує вхідний хвильовий пакет, але це один великої довжини, добре наближений плоскою хвилею. Сакурай йде прямо до площини хвилі, і ми теж робимо. Цей випадок дуже нагадує одновимірне розсіювання, при якому плоска хвиля зліва генерує вихідні хвилі в обох напрямках, а амплітуди можна обчислити за рівнянням Шредінгера для єдиного енергетичного власного стану. Різниця лише в тому, що в 3D будуть вихідні хвилі на всі боки.

Після Байма рівняння Шредінгера таке:

\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)\psi_{\vec{k}}(\vec{r})=V(\vec{r})\psi_{\vec{k}}(\vec{r}),\;\; where\;\; E_k=\frac{\hbar^2k^2}{2m}. \label{10.1.3}\]

Це\(\psi_{\vec{k}}\) ми приймаємо, щоб мати вхідний компонент площини хвилі\(e^{i\vec{k}\cdot\vec{r}}\). Загальна нормалізація не має значення, оскільки диференціальний переріз залежить лише від відношення амплітуди розсіяної хвилі до амплітуди хвилі, що йде.

Стандартний підхід до рівняння, подібного до наведеного вище, полягає в перетворенні його в інтегральне рівняння за допомогою функцій Гріна. Якщо\(V(\vec{r})\) мало (наскільки маленьким він повинен бути, стане зрозумілим пізніше) інтегральне рівняння може бути вирішене ітерацією.

Функція Гріна по суті\(G(\vec{r},\vec{k})\) є оберненою диференціальним оператором,\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)G(\vec{r},\vec{k})=\delta(\vec{r}). \label{10.1.4}\]

Це не математично унікальне визначення: зрозуміло, ми можемо додати до\(G(\vec{r},\vec{k})\) будь-якого розв'язку однорідного рівняння\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)\varphi (\vec{r},\vec{k})=0, \label{10.1.5}\]

наприклад, що надходить плоска хвиля.

Якщо записати інтегральне рівняння

\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+\int d^3r' G(\vec{r}-\vec{r}' )V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ) \label{10.1.6}\]

\(\psi_{\vec{k}}(\vec{r})\)це, безумовно, рішення вихідного рівняння Шредінгера, як це легко перевірити, застосовуючи оператор\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right) \label{10.1.7}\]

до обох сторін рівняння.

Інтегральне рівняння може бути формально вирішено ітерацією, а для «малих»\(V\) рішення буде сходитися. Але це насправді не зробить—пам'ятайте, у нас немає унікального\(G(\vec{r},\vec{k})\)! Ми повинні виправити,\(G(\vec{r},\vec{k})\) з'єднавшись краще з проблемою розсіювання, яку ми намагаємося вирішити.

Ми знаємо, що наше рішення має єдину вхідну площину хвилі, і вихідні хвилі в усіх інших напрямках, породжені взаємодією площини хвилі з потенціалом. Але рівняння Шредінгера могло б однаково описувати вхідні хвилі в інших напрямках. Визначаючи функцію Гріна та записуючи інтегральне рівняння, ми ніде не вказували віддалену форму хвильової функції, тобто ми не вимагали, щоб функція Гріна з правого боку інтегрального рівняння генерувала лише вихідні хвилі. Щоб побачити, як це зробити, ми повинні написати саму функцію Гріна як суму над хвилями, іншими словами перетворення Фур'є, і подивитися, як усунути нефізичні (для теперішньої проблеми) вхідні хвилі в цій сумі.

Явна форма функції Гріна є\[ G(r,k)=\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k}' \cdot\vec{r}}}{E_k-\frac{\hbar^2k'^2}{2m}}=-\frac{m}{2\pi^2ir\hbar^2}\int_{-\infty}^{\infty}\frac{k' dk' e^{ik'r}}{k'^2-k^2}. \label{10.1.8}\]

Зверніть увагу, що залежить\(G(r,k)\) тільки від\(\vec{k}\) наскрізного\(E_k\), і тільки від\(\vec{r}\) наскрізного\(r\), оскільки інтеграція \(\vec{k}'\)закінчена по всіх напрямках. Легко переконатися, що ця функція Гріна задовольняє диференціальному рівнянню, застосувавши диференціальний оператор до першого інтегралу вище: результат полягає в скасуванні знаменника в інтегралі, залишивши справедливий\(\int \frac{d^3k'}{(2\pi)^3}e^{i\vec{k}' \cdot\vec{r}}\), який є\(\delta\) - функція in\(\vec{r}\).

Щоб отримати другу форму\(G(r,k)\) в рівнянні вище, ми спочатку робимо кутову інтеграцію,\(d(\cos\theta)\) щоб отримати\((e^{ik'r}-e^{-ik'r})/ik' r\), а потім переставити інтеграл протягом\(-e^{-ik'r}\) терміну, перемикаючи знак\(k' \), так що він стає інтегралом від\(-\infty\) до 0 замість 0 до\(\infty\). Потім ми додаємо два члени (\(e^{ik'r}\)і\(-e^{-ik'r}\)) разом, щоб дати інтеграл від\(-\infty\) до\(\infty\). Цей інтеграл від\(-\infty\) до потім\(\infty\) робиться контурної інтеграції - принаймні, після того, як ми з'ясували, що робити з особливостями в\(k' =\pm k\).

Для визначення інтеграла контур повинен бути трохи спотворений, щоб він обходив ці полюси.

Саме в цей момент ми харчуємося нашими фізичними знаннями про ситуацію: що в процесі розсіювання, другий термін в\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+\int d^3r' G(\vec{r}-\vec{r}' )V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ), \label{10.1.9}\]

тобто термін функції Гріна має бути сумою лише над хвилями, що виходять. І ми можемо гарантувати це, спотворюючи контур інтеграції в правильному напрямку, наступним чином.

Інтеграл контуру повинен бути оцінений шляхом замикання контуру. Оскільки позитивний\(r\)\(e^{ik'r}\) йде до нуля у верхній половині\(k'\) площини, але розходиться в нижній половині, тому ми повинні замкнути контур у верхній половині площини, щоб забезпечити відсутність внеску від півкола на нескінченності. Тому, щоб отримати бажані вихідні хвилі,\(e^{ikr}\) але ні\(e^{-ikr}\), наш контур, замкнутий у верхній половині площини, повинен оточувати полюс на,\(k' =+k\) але не той, в\(k' =-k\). (\(e^{ikr}\)дійсно представляє вихідні хвилі: пригнічена залежність часу\(e^{-iEt/\hbar} =e^{-i\omega t}\), даючи\(e^{i(kr-\omega t)}\).) Іншими словами, відносна конфігурація реальної осі частини контуру та двох полюсів повинна бути:

х (полюс)

________________________________________________________________________________________________________________________________

x (полюс в\(k' =-k-i\varepsilon\)) (полюс в\(k' =+k+i\varepsilon\))

Замість того, щоб трохи зрушити контур від реальної осі, щоб уникнути полюсів, ми трохи перемістили полюси замість цього. Ці рухи нескінченно малі, тому те, що переміщується, не має ніякого значення для значення інтеграла. Зручніше переміщати полюси, як показано, тому що цей хід можна ефективно включити в інтеграл, просто додавши до знаменника нескінченно малу уявну частину:\[ G_+(r,k)=\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k}' \cdot\vec{r}}}{E_k-\frac{\hbar^2k'^2}{2m}+i\varepsilon}=-\frac{m}{2\pi^2ir\hbar^2}\int_{-\infty}^{\infty}\frac{k' dk' e^{ik'r}}{k'^2-k2-i\varepsilon}. \label{10.1.10}\]

Зверніть увагу, що ми написали\(G_+\) замість\(G\), тому що\(G\) може позначати будь-яке рішення\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)G(\vec{r},\vec{k})=\delta(\vec{r}) \label{10.1.11}\]

і ми вказуємо конкретне рішення, що має тільки вихідні хвилі. На відміну від\(G\),\(G_+\) чітко визначена і унікальна. (Є ще одне цілком правильне рішення, яке має лише вхідні хвилі, але це не має значення для проблеми розсіювання. Різниця між вхідним і вихідним розв'язками задовольняє однорідне рівняння, що має нуль з правого боку.)

Після того, як ми рухаємо полюси трохи, як описано вище, полюс на\(k' =+k+i\varepsilon\) насправді єдина сингулярність цілого, що лежить всередині контуру інтеграції (замкнутий у верхній половині площини), тому значення інтеграла є лише внесок від цього полюса, тобто\[ G_+(r,k)=-\frac{m}{2\pi^2ir\hbar^2}(2\pi i)\frac{ke^{ikr}}{2k}=-\frac{m}{2\pi\hbar^2}\frac{e^{ikr}}{r} \label{10.1.12}\]

.

Тому\(i\varepsilon\) рецепт (як його іноді називають) дійсно\(G_+\) дає нам те, що ми хочемо: рішення, що має тільки вихідні хвилі, і інтегральне рівняння стає:\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{e^{ik |  \vec{r}-\vec{r}' |}}{|\vec{r}-\vec{r}' |}V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.13}\]

Це можна написати простіше, якщо ми припускаємо, що потенціал буде локалізований, так що ми можемо взяти\(|\vec{r}|\gg |\vec{r}' |\). У цьому випадку це гарне наближення взяти\(|\vec{r}-\vec{r}' |=r\) в знаменник. Однак це наближення не може бути зроблено в експоненціальному, оскільки до порядку провідного (див. Діаграму) і хоча другий член набагато менший за перший, це фаза, яка може бути порядку єдності. Такий фактор, звичайно, повинен бути включений, щоб внески в інтеграл з різних регіонів потенціалу додавалися з правильними відносними фазами.

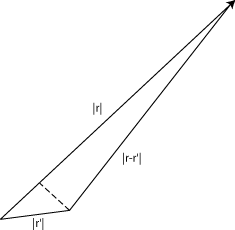
\[ k|\vec{r}-\vec{r}' |=kr-k\hat{\vec{r}}\cdot\vec{r}' =kr-\vec{k}_f\cdot\vec{r}' \label{10.1.14}\]

Тому, припускаючи,\(r\) що відстань детектора набагато більше, ніж діапазон потенціалу, ми можемо записати\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\frac{e^{i kr}}{r}\int d^3r' e^{-i \vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.15}\]

Народжене наближення

З наведеного вище рівняння наближення першого порядку до розсіяння дається заміною\(\psi\) в інтегралі праворуч на член нульового порядку\(e^{i\vec{k}\cdot\vec{r}}\),\[ \psi_{\vec{k}(Born)}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\frac{e^{i kr}}{r}\int d^3r' e^{i\vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) . \label{10.1.16}\]

Це наближення Борна. За амплітудою розсіяння\(f(\theta,\varphi)\), яку ми визначили через асимптотичну хвильову функцію:

\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{ikr}}{r} \label{10.1.17}\]

Народженим наближенням є:

\[ f_{Born}(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r' e^{i \vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) =-\frac{m}{2\pi\hbar^2}\int d^3r' e^{-i \vec{q}\cdot\vec{r}'} V(\vec{r}' ) \label{10.1.18}\]

де\(\hbar \vec{q}\) - передача імпульсу,\(\hbar \vec{q}=\hbar (\vec{k}_f-\vec{k})\). (Оскільки вхідні та вихідні моменти мають однакову величину, це легко перевірити\(q=2k\sin\theta/2\).)

Основна фізика тут полягає в тому, що частинка, розсіяна зі\(\hbar \vec{q}\) зміною імпульсу, розсіюється компонентом\(\vec{q}\) -Фур'є потенціалу - можна уявити потенціал як побудований з компонентів Фур'є, кожна з яких діє як дифракційна решітка. Поправки вищого порядку до наближення Борна відповідають послідовним розсіянням від цих решіток - ці вищі порядки генеруються ітерацією\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{e^{ik |  \vec{r}-\vec{r}' |}}{|\vec{r}-\vec{r}'|}V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.19}\]

Важливо встановити, коли наближення Народження є хорошим: іноді це не. насправді, ми просто робимо теорію збурень в маскуванні, тому нам потрібно, щоб збурень було невеликим, тобто\(\psi_{\vec{k}}(\vec{r}' )\) заміна на інтеграл праворуч у рівнянні вище повинна лише зробити\(e^{i\vec{k}\cdot\vec{r}'}\) невелика різниця від значення\(\psi_{\vec{k}}(\vec{r})\) заданого, роблячи інтеграл. Це, звичайно, досить складна вправа в самоузгодженості.

Спробуємо оцінити, яку різницю робить заміна\(\psi_{\vec{k}}(\vec{r}' )\) на\(e^{i\vec{k}\cdot\vec{r}'}\) в інтегралі для загального випадку сферично симетричного потенціалу,\(V(r)\) параметризованого глибиною\(V_0\) та діапазоном\(r_0\). Інтеграл ефективно тільки над областю розміру\(r_0\) навколо походження.

Спочатку розглянемо розсіювання низької енергії,\(kr_0<1\) скажімо, тому для цілей оцінки ми можемо замінити експоненціальний термін на 1 в області інтеграції. Ми також припускаємо, що де\(\psi\) з'являється в інтегралі на правій стороні рівняння також\(|\psi_{\vec{k}}(\vec{r}' )|\) досить близько до 1 (пам'ятайте, що інтеграл тільки над об'ємом в межах\(r_0\) або близько того від початку) і тому ми просто замінити його на 1. Іншими словами, ми припускаємо, що вхідна плоска хвиля, не різко спотворюється всередині цього обсягу, де потенціал є значним.\(e^{i\vec{k}\cdot\vec{r}'}\)

Тепер, ми припустили хвильова функція біля початку близький до 1, так що покласти це значення в integrand праворуч було краще дати значення для\(\psi_{\vec{k}}(\vec{r})\) на лівій стороні рівняння, яке досить близько до 1. Наближення дають:\[ \psi_k(0)\approx 1-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{V(r' )}{r'} ,\label{10.1.20}\]

тому наближення Народженого буде розумним при низьких енергіях (\(kr_0<1\)), якщо другий термін з правого боку набагато менше, ніж єдність.

Коли це вірно для реального потенціалу? Беручи\(V(r)\) до глибини\(V_0\) та діапазону\(r_0\), наближення Born добре, якщо:\[ \frac{m}{2\pi\hbar^2}\int_0^{r_0}4\pi r^2\frac{V_0}{r}dr\ll 1,\;\; or\;\; V_0\ll \frac{\hbar^2}{mr^2_0}. \label{10.1.21}\]

Зверніть увагу, що права сторона цієї нерівності має порядок кінетичної енергії частинки, обмеженої об'ємом, рівним діапазону потенціалу, тому наближення Борна дійсне при низьких енергіях за умови, що потенціал значно нижче сили, необхідної для зв'язаного стану.

Насправді наближення Борна краще працює при вищих енергіях, тому що коливальний термін фази в\(-\frac{m}{2\pi\hbar^2}\int d^3r' e^{-i \vec{q}\cdot\vec{r}'} V(\vec{r}' )\) скорочує значення інтеграла на порядок\(1/(kr_0)\). Це означає, що умова стає\(V_0\ll kr_0\frac{\hbar^2}{mr^2_0}\), завжди задовольняється при досить високих енергіях.

Рівняння Ліппманна-Швінгера

Це доводить освітлення, особливо в розумінні розсіювання за межами наближення Борна, переробити функцію Гріна виведення амплітуди розсіювання в більш формальній мові бюстгальтерів, кетів і операторів. Функція Гріна була введена в попередньому розділі як (неунікальна) обернена оператором\[ E_k-H_0=\left(\frac{\hbar^2}{2m}\nabla^2+E_k\right) .\label{10.1.22}\]

(Дужкове зауваження: при числовому обчисленні хвильова функція може бути вказана в точках на решітці в просторі, а диференціальний оператор, подібний до цього, буде представлений як оператор різниці, тобто як велика, але кінцева матриця, що працює на великому векторі, елементами якого були значення хвильової функції в точках на решітці. Функція Гріна буде оберненою матрицею з відповідними граничними умовами, зазначеними для забезпечення унікальності.)

Чисто формально (і після Сакурая),\(H=H_0+V\) пишучи, з\(H_0\) оператором кінетичної енергії\(\vec{p}^2/2m\), що надходить плоский хвильовий стан є розв'язком\[ H_0|\vec{k}\rangle  =E_k|\vec{k}\rangle . \label{10.1.23}\]

Ми хочемо вирішити\[ (H_0+V)|\psi\rangle  =E_k|\psi\rangle . \label{10.1.24}\]

Перетворення з диференціального рівняння в інтегральне рівняння в цій мові таке:\[ |\psi\rangle  = |\vec{k}\rangle +\frac{1}{E_k-H_0}V|\psi\rangle . \label{10.1.25}\]

Це дає непорушену вхідну хвилю для\(V=0\), і, працюючи з обох сторін рівняння\(E-H_0\), ми виявляємо, що\(|\psi\rangle\) дійсно задовольняє повне рівняння Шредінгера. Але, звичайно, це перетворення з диференціального в інтегральне рівняння має той самий недолік, що і попереднє лікування:\(H_0\) має континуум власних значень в межі нескінченного обсягу, тому операторне рівняння стає невизначеним для тих власних станів з енергією, довільно близькою до енергії, що надходить. , і це саме стани фізичної актуальності.

Щоб чітко заявити, що це дійсно проблема, яку ми вже вирішили, давайте переведемо її на більш ранню мову. Спочатку візьміть внутрішній виріб з бюстгальтером\(\langle \vec{r}|\):\[ \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\langle \vec{r}|\frac{1}{E_k-H_0}V|\psi\rangle . \label{10.1.26}\]

Далі вставте подання єдності у вигляді суми над власними станами імпульсу (і, отже,\(H_0\)) в останній член:

\[ \begin{matrix} \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \langle \vec{k}' |\frac{1}{E_k-H_0}V|\psi\rangle \\ = \langle \vec{r}|\vec{k}\rangle +\int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \frac{1}{E_k-E_k'} \langle \vec{k}' |V|\psi\rangle . \end{matrix} \label{10.1.27}\]

Нарешті, вставте інше уявлення про єдність як суму над власними станами позиції в останньому семестрі:\[ \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\int d^3r' \int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \frac{1}{E_k-E_k'}\langle \vec{k}' |\vec{r}' \rangle \langle \vec{r}' |V|\psi\rangle . \label{10.1.28}\]

Порівнюючи цей вираз з інтегральним рівнянням в попередньому обговоренні, очевидно, що вони дійсно еквівалентні, і тому правильний i\ varepsilon рецепт, щоб дати розсіяну хвильову функцію,\[ |\psi\rangle  =  |\vec{k}\rangle +\frac{1}{E_k-H_0+i\varepsilon}V|\psi\rangle  =  |\vec{k}\rangle+G_+ V|\psi\rangle \label{10.1.29}\]

де\[ G_+=\frac{1}{E_k-H_0+i\varepsilon}=\int \frac{d^3k'}{(2\pi)^3}\frac{|\vec{k}' \rangle \langle \vec{k}' |}{E_k-E_k' +i\varepsilon} \label{1.1.30}\]

в якому вигляді видно, що\(\langle \vec{r}|G_+|\vec{r}' \rangle\) таке ж, як і\(G_+(\vec{r}-\vec{r}' )\) в попередній роботі.

Це рівняння для розсіяної хвилі\(|\psi\rangle\) називається рівнянням Ліппманна-Швінгера.

Примітка: Сакурай визначає свою функцію Гріна як

\[ G_+(Sakurai)=\frac{\hbar^2}{2m}\frac{1}{E-H_0+i\varepsilon}\cdot\label{10.1.31}\]

Тепер, коли у нас є чітко визначений оператор функції Гріна\(G_+\), рівняння Ліппманна-Швінгера можна вирішити формально:\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\psi\rangle , \;\; so \;\; |\psi\rangle  = \frac{1}{1-G_+ V}|\vec{k}\rangle , \label{10.1.32}\]

з серійним рішенням\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\vec{k}\rangle +G_+ VG_+ V|\vec{k}\rangle +G_+ VG_+ VG_+ V|\vec{k}\rangle +\dots \label{10.1.33}\]

просто формальний варіант рішення, який ми знайшли раніше.

Матриця переходу

Діючи по обидва боки вищевказаного рівняння з\(V\),\[ V|\psi\rangle  =  V|\vec{k}\rangle +VG_+ V|\vec{k}\rangle +VG_+ VG_+ V|\vec{k}\rangle +\dots=T|\vec{k}\rangle \label{10.1.34}\]

визначення «матриці переходу»\(T\)\[ T=V+VG_+V+VG_+VG_+V+\dots=V+V\frac{1}{E-H_0+i\varepsilon}V+\dots \label{10.1.35}\]

З точки зору цього оператора матриці переходу можна записати розсіяну хвилю\[ |\psi\rangle = |\vec{k}\rangle  +G_+ T|\vec{k}\rangle . \label{10.1.36}\]

Порівнюючи це з\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\psi\rangle , \label{10.1.37}\]

і нагадуючи, що Народжений наближення дається\[ |\psi\rangle_{Born}= |\vec{k}\rangle +G_+ V|\vec{k}\rangle , \label{10.1.38}\]

ми бачимо, що\(T\) це свого роду узагальнений потенціал, включаючи всі умови вищого порядку, так що так само, як наближення Борна дало амплітуду розсіювання з точки зору\(V\),\[ f^{Born}(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r' e^{i \vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' )  \label{10.1.39}\]

точний результат, включаючи всі умови вищого порядку, повинен мати однакову структуру з\(T\) заміною\(V\). Звичайно, на відміну від\(V(\vec{r})\),\(T\) це не діагональна матриця в\(r\) - просторі: вона залежить від двох просторових змінних, а її перетворення Фур'є є таким чином функцією двох моментів, тобто вхідного\(\vec{k}\) і розсіяного\(\vec{k}'\). Таким чином ми знаходимо:\[ f(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r\int d^3r' e^{i \vec{k}\cdot\vec{r}-\vec{k}' \cdot\vec{r}'} T(\vec{r}' ,\vec{r})=-\frac{m}{2\pi\hbar^2}\langle \vec{k}' |T|\vec{k}\rangle . \label{10.1.40}\]

Ми замінили у\(\vec{k}_f\) виразі Born на\(\vec{k}'\). Сакурай має додатковий\((2\pi)^3\) термін праворуч, тому що він використовує\(\langle \vec{k}|\vec{k}' \rangle =\delta(\vec{k}-\vec{k'})\)\(\langle \vec{r}|\vec{k}\rangle =\frac{e^{i\vec{k}\cdot\vec{r}}}{(2\pi)^{3/2}}\), ми використовуємо\(\langle \vec{k}|\vec{k}' \rangle =(2\pi)^3\delta(\vec{k}-\vec{k'})\),\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\).

Оптична теорема

Оптична теорема пов'язує уявну частину амплітуди прямого розсіювання до загального перерізу,\[ Im\, f(\theta=0)=\frac{k\sigma_{tot}}{4\pi}. \label{10.1.41}\]

Фізичний зміст цієї спочатку таємничої теореми стане набагато зрозумілішим після того, як ми обговоримо часткові хвилі та деякі геометричні ефекти. Це говорить нам, що\(f\) не може бути реальним у всіх напрямках, і це, зокрема,\(f\) має позитивну уявну частину в прямому напрямку. Ми включили доказ тут для запису, але ви можете пропустити його зараз. Але зауважте, що цей доказ є більш загальним, ніж простий, наведений (пізніше) у розділі про часткові хвилі, в тому, що ми тут не припускаємо потенціал мати сферичну симетрію.

З виразу для\(f(\theta,\varphi)\) вище ми бачимо, що ми повинні знайти уявну частину\(\langle \vec{k}|T|\vec{k}\rangle\).

Нагадаємо, що\[ V|\psi\rangle =  T|\vec{k}\rangle , \label{10.1.42}\]

тому нам потрібно знайти\[ Im\,\langle \vec{k}|V|\psi\rangle =Im\left[\left(\langle \psi|-\langle \psi|V\frac{1}{E-H_0-i\varepsilon}\right) V|\psi\rangle \right]. \label{10.1.43}\]

Так як\(V\) це ерміт, то єдина уявна частина вищевказаного елемента матриці походить від\(i\varepsilon\), нагадуючи, що\[ \frac{1}{E-H_0-i\varepsilon}=\frac{P}{E-H_0}+i\pi\delta(E-H_0). \label{10.1.44}\]

Тому,\[ Im\,\langle \vec{k}|V|\psi\rangle =-\pi\langle \psi|V\delta(E-H_0)V|\psi\rangle . \label{10.1.45}\]

Знову використовуючи\[ V|\psi\rangle =  T|\vec{k}\rangle \label{10.1.42}\]

ми можемо переписати рівняння\[ Im\,\langle \vec{k}|T|\vec{k}\rangle =Im\,\langle \vec{k}|V|\psi\rangle =-\pi\langle \psi|V\delta(E-H_0)V|\psi\rangle =-\pi\langle \vec{k}|T^{\dagger}\delta(E-H_0)T|\vec{k}\rangle . \label{10.1.46}\]

Вставка повного набору плоских хвильових станів у кінцевий елемент матриці вище дає\[ \begin{matrix} Im\,\langle \vec{k}|T|\vec{k}\rangle =-\pi\langle \vec{k}|T^{\dagger}\delta(E-H_0)T|\vec{k}\rangle \\ =-\pi\int \frac{d^3k'}{(2\pi)^3}\langle \vec{k}|T^{\dagger}|\vec{k}' \rangle \langle \vec{k}' |T|\vec{k}\rangle \delta(E-\frac{\hbar^2k'^2}{2m}) \\ =-\pi\int \frac{d\Omega' }{(2\pi)^3}\frac{mk}{\hbar^2}|\langle \vec{k}' |T|\vec{k}\rangle |^2. \end{matrix} \label{10.1.47}\]

(Це та сама формула, що і Сакураї в 7.3: наш додатковий\((2\pi)^3\) в знаменнику тільки очевидний, тому що наші плоскі хвильові стани відрізняються від його коефіцієнтом\((2\pi)^{3/2}\).)

Зазалежне від часу формулювання теорії розсіяння

У незалежній від часу формулюванні, представленій вище, ми розв'язали рівняння Ліппманна-Швінгера, щоб знайти\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\vec{k}\rangle +G_+ VG_+ V|\vec{k}\rangle +G_+ VG_+ VG_+ V|\vec{k}\rangle +\dots \label{10.1.48}\]

де\[ G_+(E)=\frac{1}{E-H_0+i\varepsilon}=\int \frac{d^3k'}{(2\pi)^3}\frac{|\vec{k'}\rangle\langle\vec{k'}|}{E-E_{k'} +i\varepsilon} \label{10.1.49}\]

і\(E=E_k\).

(Нагадування про нашу конвенцію нормалізації хвильової функції: у нас завжди є знаменник\(2\pi\) для інтеграла\(dk\). Це означає, що оператор ідентичності як сума над операторами плоских хвиль проекції є\(I=\int \frac{d^3k}{(2\pi)^3}|\vec{k}\rangle \langle \vec{k}| \). Нормалізація - це\(\langle \vec{k}|\vec{k}' \rangle =(2\pi)^3\delta(\vec{k}-\vec{k'})\), і\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\). Sakurai використовує\(\langle \vec{k}|\vec{k}' \rangle =\delta(\vec{k}-\vec{k'})\),\(\langle \vec{r}|\vec{k}\rangle =\frac{e^{i\vec{k}\cdot\vec{r}}}{(2\pi)^{3/2}}\) і\(I=\int d^3k|\vec{k}\rangle \langle \vec{k}|\) як це робить Шанкар в главі 1, для одного виміру, сторінки 67, але пізніше, Глава 21 сторінка 585, Шанкар перейшов на нашу позначення - так що будьте обережні! Наша конвенція також використовується Баймом і Пєскіном.)

Фактично, ця функція\(G_+\) є перетворенням Фур'є пропагатора, про який ми говорили минулого семестру. Щоб побачити, як це відбувається, візьміть елемент матриці між двома власними станами позиції та перетворенням Фур'є від енергії до часу:\[ \begin{matrix} G_+(\vec{r},\vec{r'},t)=\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\langle \vec{r}|G_+|\vec{r'}\rangle \\ =\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\int \frac{d^3k'}{(2\pi)^3}\frac{\langle \vec{r}|k' \rangle \langle k' |\vec{r}' \rangle}{E-E_{k'} +i\varepsilon} \\ =\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k'}\cdot(\vec{r}-\vec{r'})}}{E-E_{k'} +i\varepsilon}. \end{matrix} \label{10.1.50}\]

Інтеграл над\(E\) знаходиться уздовж дійсної осі, а контур замкнутий в половині площини, де ціле йде до нуля для в уявному напрямку, тобто в нижній половині площини for\(t>0\) і верхній половині площини для\(t<0\). Але з показаним\(i\varepsilon\) терміном всі особливості integrand знаходяться в нижній половині площини. Отже\(G_+\), однаково нуль для\(t<0\).

Для\(t>0\),\(G_+\) це просто розповсюджувач вільних частинок між двома точками (крім фазового фактора\(-i\)):\[ G_+(\vec{r},\vec{r'},t)=-i\int \frac{d^3k'}{(2\pi)^3}e^{i\vec{k'}\cdot(\vec{r}-\vec{r'})-iE_{k'}t/\hbar} . \label{10.1.51}\]

Підсумовуючи: члени в рядовому розв'язку рівняння Ліппманна-Швінгера можна інтерпретувати як послідовні розсіяння від компонентів Фур'є потенціалу, з поширенням плоских хвиль між ними, зі знаком\(i\varepsilon\) терміна, що забезпечує наявність лише вихідних хвиль від кожного розсіювання. У трансформованій Фур'є версії вище сума над розсіюванням у всіх можливих точках, де потенціал ненульовий, з\(G_+\) поширенням між ними,\(i\varepsilon\) гарантуючи, що шлях розсіювання рухається тільки вперед у часі.

Минулого семестру ми визначили пропагатор вільних частинок як оператор\(U(t)=e^{-iH_0t/\hbar}\). Пропагатор описує розвиток хвильової функції вільних частинок у часі, так природно\(U(t)=0\) для\(t<0\). Потім Фур'є, перетворюючи пропагатор від\(t\) до\(E\), і вставляючи нескінченно малий експоненціально загасаючий коефіцієнт для визначення інтеграла на нескінченності, ми знаходимо\[ U(E)=\int_{0}^{\infty} e^{iEt/\hbar} e^{-iH_0t/\hbar}e^{-\varepsilon t/\hbar} dt=\frac{i\hbar}{E-H_0+i\varepsilon}. \label{10.1.52}\]

Відзначимо, що пропагатори\(U\) і\(G_+\) відрізняються по фактору\(i\hbar\), конкретно\[ G_+(t)=\frac{-i}{\hbar} \theta(t)e^{-iH_0t/\hbar}. \label{10.1.53}\]

Ми слідуємо позначенню Сакурая (розділ 7.11), це правильно нормована функція Гріна для залежного від часу рівняння Шредінгера вільночастинкового: це рішення\[ \left( i\hbar \frac{\partial}{\partial t}-H_0\right) G_+(t)=\delta(t) \label{10.1.54}\]

який поширюється вперед у часі. Причина, по якій пропагатори\(G_+\) відрізняються\(U\) і множником,\(i\hbar\) полягає в тому, що рівняння Ліппманна-Швінгера може генеруватися як часова послідовність, використовуючи представлення взаємодії теорії збурень вищого порядку, описане раніше в курсі, по суті розширюючись\(e^{-i(H_0+V)t/\hbar}\) як час- упорядковане розширення серії в\(V\), і кожен фактор\(V\) має супутній\(1/(i\hbar )\), ці фактори піклуються, використовуючи\(G_+\) замість\(U\).

Вправа: у цій попередній лекції ми дали термін другого порядку як:\[ c^{(2)}_n(t)=\left(\frac{1}{i\hbar}\right)^2\sum_n\int_0^t\int_0^{t'} dt' dt' ' e^{-i\omega_f(t-t' )}\langle f|V_S(t' )|n\rangle e^{-i\omega_n(t' -t' ' )}\langle n|V_S(t' ' )|i\rangle e^{-i\omega it' '} \label{10.1.55}\]

Припустимо,\(V\) що потенціал постійний в часі. Фур'є перетворюють цей вираз від\(t\) до\(E\)\(E=\hbar \omega\), і встановлюють, що воно має структуру\(G_+(E)VG_+(E)VG_+(E)\).

Народжений переріз із теорії, що залежить від часу

У лекції з теорії збурень, залежної від часу, встановлено, що до провідного порядку збурень швидкість переходу від початкового стану\(i\) до кінцевого стану\(f\) задається Золотим правилом Фермі:\[ R_{i\to f}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i). \label{10.1.56}\]

Ми можемо використовувати цей результат, щоб знайти - у порядку початку - швидкість розсіювання від вхідної площини хвилі в будь-який вихідний плоский хвильовий стан, що має ту ж енергію, і, отже, додаючи швидкість над напрямками плоских хвиль, що вказують в межах заданого малого твердого кута\(d\Omega\), відновити наближення Борна.

Концептуально, хоча, це трохи складно. З наведеного вище рішення рівняння Шредінгера ми знаємо, що виходить хвиля є сферичною, тому в певному напрямку амплітуда зменшується. Але це не відбувається з плоскою хвилею! Найясніший спосіб впоратися з цим - поставити систему у велику коробку, куб сторони\(L\), з періодичними граничними умовами. Це полегшує підрахунок станів та правильну нормалізацію плоских хвиль - звичайно, в межі великої коробки плоскі хвилі утворюють повний набір, тому будь-яка сферична хвиля може бути виражена як сума над цими площинними хвилями.

У цьому розділі ми використовуємо коробчати-нормовані плоскі хвилі:\[ |\vec{k}\rangle =\frac{1}{L^{3/2}}e^{i\vec{k}\cdot\vec{r}},\;\; \langle \vec{k'}|\vec{k}\rangle =\delta_{\vec{k}\vec{k'}} . \label{10.1.57}\]

Так\[ \langle f|V|i\rangle =\frac{1}{L^3}\int d^3re^{-i\vec{k}_f\cdot\vec{r}}V(\vec{r}) e^{i\vec{k}_i\cdot\vec{r}}=\frac{1}{L^3}\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r}) \label{10.1.58}\]

де імпульс передається частці\(\hbar \vec{q}=\hbar (\vec{k}_f-\vec{k}_i)\).

Важливо зазначити, що ми приймаємо вхідну хвилю, щоб бути лише одним із нормованих плоских хвильових станів, що задовольняють періодичні граничні умови коробки, так що тепер вхідний струм, будучи лише з однієї з цих плоских хвиль, є\[ j_{in}=|\psi|^2v=\frac{1}{L^3}\frac{p}{m}. \label{10.1.59}\]

Золотим правилом стає\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i)d\Omega \label{10.1.60}\]

\(f\)позначаючи плоску хвилю, що йде назовні в межах твердого кута\(d\Omega\).

Тепер\(\delta\) - функція просто підраховує кількість станів, доступних при правильній (початковій) енергії, в межах заданого кінцевого твердого кута напрямку. Щільність станів в імпульсному просторі (для\(L^3\) обсягу реального простору) - це один стан в кожному об'ємі моменту-простору\((2\pi\hbar)^3/L^3\), тому, використовуючи\(dE/dp=p/m\), щільність станів в енергії для вихідного твердого кута\(d\Omega\) дорівнює\(L^3mpd\Omega/(2\pi\hbar)^3\).

Збираємо все це разом\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\frac{1}{L^3}\int d^3xe^{-i\vec{q}\cdot\vec{x}}V(\vec{x})|^2L^3mpd\Omega/(2\pi\hbar)^3. \label{10.1.61}\]

Швидкість переходу, швидкість розсіювання в\(d\Omega\), - це всього лише падаючий струм, помножений на нескінченно малий переріз розсіювання\(d\sigma(\theta,\varphi)\) (це було наше визначення\(d\sigma\)),

\[ j_{in}(\frac{d\sigma(\theta,\varphi)}{d\Omega})d\Omega=R_{i\to(f\; in\; d\Omega)} \label{10.1.62}\]

тому що наше визначення\(R_{i\to(f\; in\; d\Omega)}\) включало відповідним чином нормалізовану вхідну хвилю.

Отже, нарешті\[ \frac{d\sigma(\theta,\varphi)}{d\Omega}=\frac{R_{i\to(f\; in\; d\Omega)}}{j_{in}d\Omega}=\frac{m}{p}\frac{2\pi}{\hbar} |\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2mp/(2\pi\hbar)^3=|\frac{m}{2\pi\hbar^2}\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2. \label{10.1.63}\]

Примітка: версія континууму.

\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i)d\Omega. \label{10.1.60}\]

У версії континууму\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\), так що елемент матриці термін просто\(|\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2\). Енергія\(\delta\) - функція має сенс лише всередині інтеграла, в даному випадку над малим обсягом виходять станів розсіювання в твердому куті\(d\Omega\) і енергії, рівній енергії, що надходить. Але цей інтеграл над\(k'\) - простір повинен включати в себе\(1/(2\pi)^3\) фактор, згідно з нашим правилом, що дає вихідний термін фазового простору\[ \int \frac{d^3k'}{(2\pi)^3}\delta(E_{k'}-E_k)=d\Omega\int \frac{k'^2dk' }{(2\pi)^3} \delta\left(\frac{\hbar^2k'^2}{2m}-\frac{\hbar^2k^2}{2m}\right)=d\Omega\frac{k^2}{(2\pi)^3}\frac{m}{\hbar^2k}=d\Omega\frac{mp}{(2\pi\hbar)^3}. \label{10.1.64}\]

Це встановлює, що наші конвенції про нормалізацію континууму дають той же результат, що і отриманий від нормалізації коробки.

Розсіювання електронів від атомів

Цей же підхід, використовуючи Золоте правило для виведення швидкості розсіювання провідного порядку, корисний для аналізу розсіювання швидких електронів атомами. Проблема з повільними електронами полягає в тому, що хвильова функція повинна бути антисиметричною по відношенню до всіх присутніх електронів. Ми припускаємо, що швидкі електрони мало перекриваються з функціями атомних електронних хвиль у просторі імпульсу, тому нам не доведеться турбуватися про симетрію.

При цьому наближенні після Сакурая (сторінка 431) елемент матриці амплітуди розсіювання є\[ \int d^3re^{i\vec{q}\cdot\vec{r}}\langle n|\left( -\frac{Ze^2}{r}+\sum_i\frac{e^2}{|\vec{r}-\vec{r}_i|}\right) |0\rangle \label{10.1.65}\]

де потенційний термін\(V(\vec{x})\) - це те, що від ядра, плюс відштовхування від інших електронів у позиціях\(\vec{x}_i\). Прийняття кінцевого атомного стану\(n\) допускає можливість непружного розсіювання.

Так як відстань\(r\) розсіяного електрона від ядра не має нічого спільного з атомним станом, то\(n=0\) для ядерного внеску, який тоді якраз кулонівське розсіювання, і\[ \int d^3r\frac{e^{i\vec{q}\cdot\vec{r}}}{r}=\frac{4\pi}{q^2}. \label{10.1.66}\]

(Щоб зробити це інтеграл, покласти в коефіцієнт збіжності\(e^{-\varepsilon r}\) потім нехай\(\varepsilon\to 0\).)

Термін за участю атомних електронів - інша справа: для\(i^{th}\) електрона інтеграція по координаті розсіяного електрона дає множник\((4\pi/q^2)e^{i\vec{q}\cdot\vec{r}_i}\), але тверда частина - знаходження значення матричного елемента цього оператора між атомними станами. Зверніть увагу, що це всього лише перетворення Фур'є електростатичного потенціалу від щільності заряду\(i^{th}\) електрона,

\( \nabla^2V_i(\vec{r}i)=4\pi\rho_i(\vec{r}_i)\)перетворюється на\(V_i(\vec{q})=(4\pi/q^2)\rho_i(\vec{q})\) і\(\rho_i(\vec{r})=e\delta(\vec{r}-\vec{r}_i)\) Фур'є перетворюється на\(e(e^{i\vec{q}\cdot\vec{r}_i})\).

Форм-фактор

Тоді для пружного розсіювання внесок атомних електронів просто інтерпретується: їх щільність заряду породжує потенціал звичайним електростатичним рівнянням, а (швидкий) електрон розсіюється цим потенціалом. Для непружного розсіяння оцінюється перетворення Фур'є електронної густини між різними атомними станами. В обох випадках елемент матриці називається форм-фактором\(F_n(\vec{q})\) для розсіювання, власне\(ZF_n(\vec{q})=\langle n|\sum_i e^{i\vec{q}\cdot\vec{r}_i}|0\rangle \). Нормалізуючий коефіцієнт\(Z\) вводять так, щоб для пружного розсіювання,\(F_n(\vec{q})\to 1\) як\(q\to0\).

Так форм-фактор являє собою карту щільності заряду в\(q\) - просторі. Вимірюючи швидкість розсіювання під різними кутами, і аналізуючи Фур'є, можна розмежувати розподіл заряду в звичайному просторі. Ця ж методика працює для ядер, а насправді для частинок - нейтрон, наприклад, хоча і електрично нейтральний, має нетривіальний розподіл електричного заряду в межах свого об'єму, виявлений розсіюванням дуже швидких електронів.

Більш загальні форм-фактори описують розподіл спина, а також часову залежність розподілів заряду або спина в збуджених системах. Всі вони можуть бути виміряні за допомогою відповідним чином розроблених експериментів розсіювання.