9.3: Ван дер Ваальса сили між атомами

Вступ

Ідеальне рівняння стану газу\(PV=NkT\) явно не здатне описати фактичні гази при низьких температурах, так як вони зазнають переривчастої зміни об'єму і стають рідинами. У 1870-х роках голландський фізик Ван дер Ваальс придумав поліпшення: закон газу, який визнавав молекули взаємодіяли між собою. Він поставив два параметри, щоб імітувати цю взаємодію. Перший, приваблива міжмолекулярна сила на великих відстанях, допомагає зібрати газ разом і, отже, зменшує необхідний зовнішній тиск для утримання газу в заданому обсязі - газ трохи тонший біля стінок. Приваблива сила далекого діапазону може бути представлена негативним потенціалом\(-aN/V\) при відході від стінок - молекули біля стінок притягуються всередину, ті, що знаходяться в основній масі, притягуються однаково у всіх напрямках, тому ефективно тяжіння на дальній відстані еквівалентно потенційному добре розширюється по всьому об'єму, закінчуючи впритул до стін. Отже, щільність газу\(N/V\) біля стін зменшується в рази\(e^{-E/kT}=e^{-aN/VkT}\cong 1-aN/VkT\). Тому тиск, виміряний у вміщує стінки, йде від злегка розрідженого газу, так\(P=(N/V)kT\) стає\(P=(N/V)(1-aN/VkT)kT\), або\((P+a(N/V)^2)V=NkT\). Другий параметр, доданий ван дер Ваальсом, полягав у врахуванні скінченного молекулярного об'єму. Справжній газ не можна стиснути невизначено - він стає рідиною, для всіх практичних цілей нестисливою. Він представляв це\(V\) заміною обсягу на\(V-Nb\),\(Nb\) іменується як «виключений обсяг», грубо кажучи об'ємом молекул. Введення в ці два терміни дає його відоме рівняння\[ \left[ P+a\left(\frac{N}{V}\right)^2\right] (V-Nb)=NkT. \label{9.3.1}\]

Це досить грубе наближення насправді дає набори ізотерм, що представляють основну фізику фазового переходу досить добре. (Для отримання більш детальної інформації та просвітницької дискусії див., наприклад, Додаток D теплофізики, Р.Байрляйн.)

Атоми водню наземного стану

Наш інтерес тут полягає в розумінні важкої сили притягання ван дер Ваальса між електрично нейтральними атомами і молекулами в квантово-механічному відношенні. Почнемо з найпростішого можливого прикладу, двох атомів водню, обидва знаходяться в основному стані:

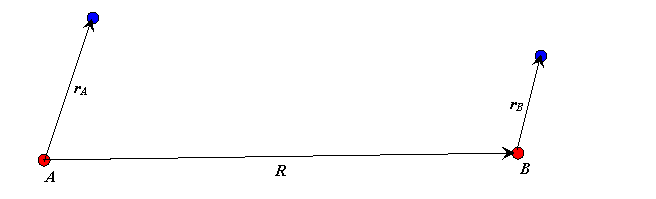
Ми позначаємо атоми\(A\) і\(B\), вектори від протонів до положення електронів позначаються\(\vec{r_A}\) і\(\vec{r_B}\) відповідно, і\(\vec{R}\) є вектором від протона\(A\) до протона\(B\).

Тоді гамільтоніан\(H=H^0+V\), де\[ H^0=-\frac{\hbar^2}{2m}(\nabla^2_A+\nabla^2_B)-\frac{e^2}{r_A}-\frac{e^2}{r_B} \label{9.3.2}\]

і електростатична взаємодія між двома атомами\[ V=\frac{e^2}{R}+\frac{e^2}{|\vec{R}+\vec{r_B}-\vec{r_A}|}-\frac{e^2}{|\vec{R}+\vec{r_B}|}-\frac{e^2}{|\vec{R}-\vec{r_A}|} \label{9.3.3}\]

Основний стан\(H^0\) є лише добутком наземних станів атомів\(A,B\), тобто\[ |0\rangle =|100\rangle_A\otimes |100\rangle_B. \label{9.3.4}\]

Припускаючи тепер, що відстань між двома атомами набагато більше, ніж їх розмір, ми можемо розширити взаємодію\(V\) за малими параметрами\(r_A/R,\;  r_B/R\). Як можна було б підозрювати з наведеної вище діаграми, провідними термінами порядку в електростатичній енергії є лише термінами дипольно-дипольної взаємодії:\[ V=-e^2(\vec{r_A}\cdot \vec{\nabla})(\vec{r_B}\cdot \vec{\nabla})\frac{1}{R}=e^2\left[ \frac{\vec{r_A}\cdot \vec{r_B}}{R^3}-\frac{3(\vec{r_A}\cdot \vec{R})(\vec{r_B}\cdot \vec{R})}{R^5}\right] \label{9.3.5}\]

Беручи тепер вісь z у напрямку\(\vec{R}\), ця енергія взаємодії\[ V=\frac{e^2}{R^3}(x_Ax_B+y_Ay_B-2z_AZ_B) \label{9.3.6}\]

Тепер корекція першого порядку до енергії основного стану двоатомної системи від цієї взаємодії є\(E^1_n=\langle n^0|H^1|n^0\rangle\), де тут\(H^1=V\) і\(|n^0\rangle =|100\rangle_A\otimes |100\rangle_B\). Починаючи з першого семестру\(x_Ax_B\) в\(V\)\[ (_A\langle 100|\otimes_B\langle 100|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle 100|x_A|100\rangle_A)(_B\langle 100|x_B|100\rangle_B) \label{9.3.7}\]

явно дорівнює нулю, оскільки наземні стани сферично симетричні. Аналогічно, інші терміни в\(V\) дорівнюють нулю першому порядку.

Нагадаємо, що енергетична корекція другого порядку є\(E^2_n=\sum_{m\neq n} \frac{|\langle m0|H^1|n^0\rangle |^2}{E^0_n-E^0_m} \).

Тобто,\[ E^{(2)}=\sum_{\begin{matrix}n,l,m\\ n′,l′,m′ \end{matrix}} \frac{|(_A\langle nlm|\otimes_B\langle n′l′m′|)V(|100\rangle_A\otimes |100\rangle_B)|^2}{2E_1-E_n-E_{n′}}. \label{9.3.8}\]

Типовим терміном тут є\[ (_A\langle nlm|\otimes_B\langle n′l′m′|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle nlm|x_A|100\rangle_A)(_B\langle n′l′m′|x_B|100\rangle_B), \label{9.3.9}\]

тож одноатомні матричні елементи саме ті, які ми обговорювали для ефекту Старка (як ми очікували - це електростатична взаємодія!). Як і раніше, тільки\(l=1,\;\;  l′=1\) сприяти. Щоб зробити приблизну оцінку розміру\(E^{(2)}\), ми можемо використовувати той самий трюк, який використовується для квадратичного ефекту Старка: замінити знаменники константою\(2E_1\) (інші терміни набагато менші для зв'язаних станів, а континуальні стани мають невеликі терміни перекриття в чисельнику). Потім сума над проміжними станами\(n,l,m,n′,l′,m′\) може бути прийнята абсолютно необмеженою, включаючи навіть наземний стан, що дає\[ \sum_{\begin{matrix}n,l,m\\ n′,l′,m′ \end{matrix}} (|nlm\rangle_A\otimes |n′l′m′\rangle_B)(_A\langle nlm|\otimes_B\langle n′l′m′|)=I, \label{9.3.10}\]

оператор ідентичності. У цьому наближенні, так само, як і для ефекту Старка,\[ E^{(2)}\simeq \frac{e^4}{R^6}\frac{1}{2E_1}(_A\langle 100|\otimes_B\langle 100|)(x_Ax_B+y_Ay_B-2z_AZ_B)^2(|100\rangle_A\otimes |100\rangle_B) \label{9.3.11}\]

де\(E_1=-1\) Ryd., Так що це зниження енергії.

При множенні\((x_Ax_B+y_Ay_B-2z_AZ_B)^2\) перехресні члени матимуть очікувані значення нулю. Функція хвилі наземного стану симетрична, тому все, що нам потрібно\(\langle 100|x^2|100\rangle =a^2_0\),\(a_0\) це де радіус Бора.

Це дає

\[ E^{(2)}\simeq \frac{e^4}{R^6}\frac{1}{2E_1}6a^4_0\simeq -6\frac{e^2}{R}\left( \frac{a_0}{R}\right)^5 \label{9.3.12}\]

використовуючи\(E_1=-e^2/2a_0\). Майте на увазі, що це наближення, але досить гарне - більш точний розрахунок замінює 6 на 6,5.

Сили між атомом водню 1 с і атомом водню 2 р

З одним атомом в,\(|100\rangle\) а іншим у\(|210\rangle\), скажімо, типовим терміном провідного порядку буде

\[ (_A\langle 100|\otimes_B\langle 210|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle 100|x_A|100\rangle_A)(_B\langle 210|x_B|100\rangle_B), \label{9.3.13}\]

і це, безумовно, нуль, як і всі інші провідні терміни. Байм (Лекції з квантової механіки) зробив висновок з цього, що немає провідного порядку енергетичної корекції між двома атомами водню, якщо один з них знаходиться в основному стані. Це невірно: перший збуджений стан двоатомної системи (без взаємодії) вироджується, тому, точно так само, як і для 2-D простого гармонійного осцилятора, розглянутого в попередній лекції, ми повинні діагоналізувати збуреність в підпросторі цих вироджених перших збуджених станів. (У цьому розділі ми досить уважно стежимо за чудовим лікуванням у квантовій механіці, C. Cohen-Tannoudji et al.)

Простір вироджених перших збуджених станів двох невзаємодіючих атомів охоплюється кетами продуктового простору:\[ \begin{matrix} (|100\rangle_A\otimes |200\rangle_B), &(|200\rangle_A\otimes |100\rangle_B),&(|100\rangle_A\otimes |211\rangle_B),&(|211\rangle_A\otimes |100\rangle_B),\\ (|100\rangle_A\otimes |210\rangle_B),&(|210\rangle_A\otimes |100\rangle_B),&(|100\rangle_A\otimes |21-1\rangle_B),&(|21-1\rangle_A\otimes |100\rangle_B). \end{matrix} \label{9.3.14}\]

Таким чином, завдання полягає в тому, щоб діагоналізувати\(V=\frac{e^2}{R^3}(x_Ax_B+y_Ay_B-2z_AZ_B)\) в цьому восьмивимірному підпросторі.

Почнемо з представлення\(V\) як\(8\times 8\) матриці, використовуючи ці стани в якості основи. По-перше, зауважте, що всі діагональні елементи матриці нуль - у всіх них ми знаходимо середнє значення x, y або z для одного з атомів в основному стані. По-друге, пишучи\(V=\frac{e^2}{R^3}(\vec{r_A}\cdot \vec{r_B}-3z_AZ_B)\), видно, що\(V\) незмінна, якщо система обертається навколо осі z (лінія, що з'єднує два протони). Це означає, що комутатор\([V,L_z]=0\), де\(L_z\) сумарна складова моменту моменту в напрямку z, так\(V\) буде мати тільки ненульові елементи матриці між станами, що мають однакову загальну суму\(L_z\). По-третє, від парності (або Вігнер-Еккарта) всі елементи матриці в підпросторі, що охоплюється,\((|100\rangle_A\otimes |200\rangle_B),\; (|200\rangle_A\otimes |100\rangle_B)\) повинні бути нулем.

Це зводить ненульову частину\(8\times 8\) матриці до прямого добутку трьох\(2\times 2\) матриць, що відповідає трьом значенням\(L_z=m\). Наприклад,\(m=0\) підпростір охоплюється\((|100\rangle_A\otimes |210\rangle_B),\; (|210\rangle_A\otimes |100\rangle_B)\). Діагональні елементи\(2\times 2\) матриці дорівнюють нулю, позадіагональні елементи рівні\(-2\frac{e^2}{R^3}(_A\langle 100|z_A|210\rangle_A)(_B\langle 210|Z_B|100\rangle_B)\), де ми зберегли непотрібні мітки,\(A,B\) щоб зрозуміти, звідки походить цей термін. (\(x_A\)І\(y_A\) умови не сприятимуть\(m=0\).)

Тепер це простий інтеграл над хвилевими функціями водню. Три\(2\times 2\) матриці мають вигляд\[ \begin{pmatrix} 0&k_m/R^3\\ k_m/R^3 &0 \end{pmatrix} \label{9.3.15}\]

(за позначенням Коена-Таннуджі) де\(k_m\sim e^2a^2_0\) і енергії власні значення\(\pm k_m/R^3\), з відповідними власними метками\( (1/\sqrt{2})[(|100\rangle_A\otimes |210\rangle_B)\pm (|210\rangle_A\otimes |100\rangle_B)]\).

Таким чином, для двох атомів водню, одного в основному стані і одного в першому збудженому стані, енергія взаємодії ван дер Ваала йде набагато важливішою\(1/R^3\), ніж\(1/R^6\) енергія для двох атомів водню в основному стані. Зверніть увагу також, що вони\(1/R^3\) можуть бути позитивними або негативними, залежно від того, чи атоми знаходяться в парному або непарному стані, тому атоми іноді відштовхують один одного.

Нарешті, якщо два атоми спочатку знаходяться в стані\((|100\rangle_A\otimes |210\rangle_B)\), зверніть увагу, що це не власний стан гамільтоніана, коли взаємодія включена. Записуючи стан як суму парних і непарних станів, які мають дещо відмінні фазові частоти від різниці енергій, ми знаходимо рух збудження вперед і назад між двома атомами з періодом\(hR^3/2k_{m=0}\).