2.2: Лінійна алгебра

Вступ

Ми бачили, що в квантовій механіці стан електрона в деякому потенціалі задається хвильовою функцією\(\psi(\vec x,t)\), а фізичні змінні представлені операторами цієї хвильової функції, такими як імпульс у напрямку x\(p_x =-i\hbar\partial/\partial x\). Хвильове рівняння Шредінгера - це лінійне рівняння, що означає, що якщо\(\psi_1\) і\(\psi_2\) є розв'язками, то так є\(c_1\psi_1+c_2\psi_2\), де\(c_1, c_2\) довільні комплексні числа.

Ця лінійність множин можливих розв'язків істинна загалом у квантовій механіці, як і представлення фізичних змінних операторами на хвильових функціях. Математична структура, що описується, лінійна множина можливих станів і множин операторів на цих станах, фактично є лінійною алгеброю операторів, що діють на векторний простір. Відтепер це мова, якою ми будемо користуватися більшу частину часу. Для уточнення наведемо деякі визначення.

Що таке векторний простір?

Прототиповий векторний простір, звичайно, є сукупністю дійсних векторів у звичайному тривимірному просторі, ці вектори можуть бути представлені тріями дійсних чисел, що\((v_1,v_2,v_3)\) вимірюють компоненти у напрямках x, y та z відповідно.

Основними властивостями цих векторів є:

• будь-який вектор, помножений на число, є іншим вектором в просторі,\(a(v_1,v_2,v_3)=(av_1,av_2,av_3)\);
• сума двох векторів - це ще один вектор у просторі, який задається просто додаванням відповідних компонентів разом:\((v_1+w_1,v_2+w_2,v_3+w_3)\).

Ці дві властивості разом називаються «закриттям»: додавання векторів і множення їх на числа не може вивести вас з простору.

• Ще одна властивість полягає в тому, що існує унікальний нульовий вектор\((0,0,0)\) і кожен вектор має адитивну обернену,\((-v_1,-v_2,-v_3)\) яка додана до вихідного вектора, дає нульовий вектор.

Математики узагальнили визначення векторного простору: загальний векторний простір має перераховані вище властивості для тривимірних дійсних векторів, але операції додавання і множення на число узагальнюються до більш абстрактних операцій між більш загальними сутностями. Однак оператори обмежуються комутативними та асоціативними.

Зверніть увагу, що перелік необхідних властивостей для загального векторного простору не включає, що вектори мають величину - це буде додатковою вимогою, що дає те, що називається нормованим векторним простором. Детальніше про це пізніше.

Щоб перейти від звичного тривимірного векторного простору до векторних просторів, що мають відношення до квантової механіки, спочатку дійсні числа (компоненти вектора і можливі множники) повинні бути узагальнені до комплексних чисел, а по-друге трикомпонентний вектор йде n компонентним вектором. Послідовний n -мірний складний простір достатній для опису квантової механіки моменту моменту, важливого предмета. Але для опису хвильової функції частинки в коробці потрібен нескінченний розмірний простір, один вимір для кожної складової Фур'є, а для опису хвильової функції для частинки на нескінченній лінії потрібен набір всіх нормалізованих неперервних диференційованих функцій на цій лінії. На щастя, всі ці узагальнення є кінцевими або нескінченними множинами комплексних чисел, тому вимоги математиків до векторного простору комунітативності та асоціативності завжди тривіально задовольняються.

Ми використовуємо позначення Дірака для векторів,\(|1\rangle,|2\rangle\) і називаємо їх «kets», так, на його мові, якщо\(|1\rangle,|2\rangle\) належать до простору, так і\(c_1|1\rangle +c_2|2\rangle\) для довільних складних констант\(c_1, c_2\). Оскільки наші вектори складаються з комплексних чисел, множення будь-якого вектора на нуль дає нульовий вектор, а адитивний зворотний задається шляхом зворотного зміни знаків всіх чисел у векторі.

Зрозуміло, що сукупність розв'язків рівняння Шредінгера для електрона в потенціалі задовольняє вимогам до векторного простору:\(\psi(\vec x,t)\) це всього лише комплексне число в кожній точці простору, тому в формуванні беруть участь тільки комплексні числа\(c_1\psi_1+c_2\psi_2\), а комутативність, асоціативність тощо слідують відразу.

Векторний простір розмірності

\( |1\rangle ,|2\rangle ,|3\rangle\)Вектори лінійно незалежні, якщо\[ c_1|1\rangle +c_2|2\rangle +c_3|3\rangle =0 \tag{2.2.1}\]

має на увазі\[ c_1=c_2=c_3=0 \tag{2.2.2}\]

Векторний простір є n-мірним, якщо максимальна кількість лінійно незалежних векторів у просторі дорівнює n.

Такий пробіл часто називають\(V^n(C)\), або\(V^n(R)\) якщо використовуються тільки дійсні числа.

Тепер векторних просторів з скінченною розмірністю n явно недостатньо для опису функцій неперервної змінної x. Але їх варто переглянути тут: як ми вже згадували, вони чудово підходять для опису квантованого кутового імпульсу, і вони служать природним введенням до нескінченновимірних просторів, необхідних для опису просторових хвильових функцій.

Множина n лінійно незалежних векторів у n -вимірному просторі є основою —будь-який вектор можна записати унікальним способом у вигляді суми за базису:\[ |V\rangle=\sum v_i|i\rangle \tag{2.2.3}\]

Перевірити унікальність можна, взявши різницю між двома нібито різними сумами: це буде лінійне відношення між незалежними векторами, протиріччя.

Оскільки всі вектори в просторі можна записати у вигляді лінійних сум над елементами базису, сума кратних будь-яких двох векторів має вигляд:\[ a|V\rangle+b|W\rangle=\sum (av_i+bw_i)|i\rangle \tag{2.2.4}\]

Внутрішні простори продукту

Векторні простори актуальності в квантовій механіці також мають операцію асоціації числа з парою векторів, узагальнення точкового добутку двох звичайних тривимірних векторів,\[ \vec a, \vec b =\sum a_ib_i \tag{2.2.5}\]

Слідом за Діраком запишемо внутрішній добуток двох ket-векторів\(|V\rangle,|W\rangle\) як\(\langle W|V\rangle\). Дірак називає цю\(\langle \; | \; \rangle\) форму «дужкою», що складається з «бюстгальтера» та «кету». Це означає, що кожен вектор ket\(|V\rangle\) має пов'язаний бюстгальтер\(\langle V|\). Для випадку дійсного n -вимірного вектора\(|V\rangle,\langle V|\) однакові, але ми вимагаємо для більш загального випадку, що\[ \langle W|V\rangle=\langle V|W\rangle^*\tag{2.2.6}\]

де\(*\) позначає складний сполучений. Це означає, що для кеда\((v_1,...,v_n)\) бюстгальтер буде\((v_1^*,...,v_n^*)\). (Власне, бюстгальтери зазвичай записуються як рядки, кети як стовпці, так що внутрішній твір дотримується стандартних правил множення матриці.) Очевидно, що для n -вимірного комплексного вектора\(\langle V|V\rangle\) є дійсним і додатним, крім нульового вектора:

\[ \langle V|V\rangle=\sum_1^n |v_i|^2 \tag{2.2.7}\]

Для більш загальних внутрішніх просторів добутку, розглянутих пізніше, ми\(\langle V|V\rangle\) вимагаємо бути додатними, за винятком нульового вектора. (Ці вимоги обмежують класи векторних просторів, які ми розглядаємо, наприклад, немає метрики Лоренца, але всі вони задовольняються просторами, що мають відношення до нерелятивістської квантової механіки.)

Норма\(|V\rangle\) при цьому визначається\[ |V|=\sqrt{\langle V|V\rangle} \tag{2.2.8}\]

If\(|V\rangle\) є членом\(V^n(C)\), так є\(a|V\rangle\), для будь-якого комплексного числа\(a\).

Ми вимагаємо, щоб внутрішня операція виробу переїхала з множенням на число, тому

\[ \langle W|(a|V\rangle)=a\langle W|V\rangle \tag{2.2.9}\]

Складним сполученням правої сторони є\(a^*\langle V|W\rangle\). Тому для узгодженості бюстгальтер, відповідний ket,\(a|V\rangle\) повинен бути\(\langle V|a^*\) - у будь-якому випадку очевидним з визначення бюстгальтера в n складних розмірах, наведених вище.

Звідси випливає, що якщо\[ |V\rangle=\sum v_i|i\rangle, \; |W\rangle=\sum w_i|i\rangle, \; then \; \langle V|W\rangle=\sum v_i^*w_j \langle i|j\rangle \tag{2.2.10}\]

Побудова ортонормальної основи: процес Грама-Шмідта

Щоб мати щось краще схоже на стандартний точковий добуток звичайних трьох векторів, нам потрібно\(\langle i|j\rangle=\delta_{ij}\), тобто побудувати ортонормальну основу в просторі. Існує проста процедура для цього, яка називається процесом Грама-Шмідта. Почнемо з лінійно незалежного набору базисних векторів\(|1\rangle, |2\rangle, |3\rangle\),,...

Спочатку нормалізуємо\(|1\rangle\), розділивши її на норму. Викликати нормалізований вектор\(|I\rangle\). Тепер\(|2\rangle\) не може бути паралельним\(|I\rangle\), тому що початкова основа була лінійно незалежних векторів, але\(|2\rangle\) в цілому має ненульову складову паралельно\(|I\rangle\), рівну\(|I\rangle\langle I|2\rangle\), так як\(|I\rangle\) нормалізується. Тому вектор\(|2\rangle-|I\rangle\langle I|2\rangle\) перпендикулярний\(|I\rangle\), як легко перевіряється. Також легко обчислити норму цього вектора, і розділити по ньому\(|II\rangle\), щоб отримати, другий член ортонормальної основи. Далі беремо\(|3\rangle\) і віднімаємо його складові по напрямках\(|I\rangle\) і\(|II\rangle\), нормалізуємо залишок і так далі.

У n -вимірному просторі, побудувавши ортонормальну основу з членами\(|i\rangle\), будь-який вектор\(|V\rangle\) можна записати як стовпчастий вектор,\[ |V\rangle= \sum v_i |i\rangle= \begin{pmatrix}v_1 \\ v_2 \\ . \\ . \\ v_n \end{pmatrix} \, , \; where \; |1\rangle= \begin{pmatrix}1 \\ 0 \\ . \\ . \\ 0 \end{pmatrix} \; and \: so \: on. \tag{2.2.11}\]

Відповідний бюстгальтер є\(\langle V|=\sum v_i^*\langle i|\), який ми пишемо у вигляді вектора рядка з елементами комплексно спряжені,\(\langle V|=(v_1^*,v_2^*,...v_n^*)\). Ця операція, переходячи від стовпців до рядків і приймаючи складний сполучений, називається прийняттям суміжних, а також може бути застосована до матриць, як ми побачимо коротко.

Причина представлення бюстгальтера у вигляді рядка полягає в тому, що внутрішній добуток двох векторів потім задається стандартним множенням матриці:\[ \langle V|W\rangle=(v_1^*,v_2^*,...,v_n^*) \begin{pmatrix}w_1\\ . \\ . \\ w_n \end{pmatrix} \tag{2.2.12}\]

(Звичайно, це працює лише з ортонормальною основою.)

Нерівність Шварца

Нерівність Шварца - це узагальнення до будь-якого внутрішнього простору добутку результату\(|\vec a ,\vec b|^2 \le |\vec a|^2|\vec b|^2\) (або\(\cos^2 \theta \le1\)) для звичайних тривимірних векторів. Знак рівності в цьому результаті тримається лише тоді, коли вектори паралельні. Щоб узагальнити до вищих вимірів, можна просто зазначити, що два вектори знаходяться в двовимірному підпросторі, але освітлюючим способом розуміння нерівності є написання вектора у\(\vec a\) вигляді суми двох компонентів, однієї паралельної\(\vec b\) та однієї перпендикулярної\(\vec b\). Компонент паралельно\(\vec b\) є справедливим\(\vec b(\vec a\cdot \vec b)/|\vec b|^2\), так що компонент перпендикулярно до\(\vec b\) є вектор\(\vec a_{\bot}=\vec a-\vec b(\vec a\cdot\vec b)/|\vec b|^2 \). Підставляючи цей вираз в\(\vec a_{\bot}\cdot\vec a_{\bot} \ge0 \), слід нерівність.

Цю ж точку можна зробити в загальному внутрішньому просторі добутку: якщо\(|V\rangle\),\(|W\rangle\) два вектори, то\[ |Z\rangle=|V\rangle-\frac{|W\rangle \langle W|V\rangle}{|W|^2} \tag{2.2.13}\]

є складовою\(|V\rangle\) перпендикулярно\(|W\rangle\), як це легко перевірити, взявши його внутрішній продукт с\(|W\rangle\).

Тоді\[ \langle Z|Z\rangle \ge0 \;\; gives\; immediately\;\; |\langle V|W\rangle|^2 \le |V|^2|W|^2 \tag{2.2.14}\]

Лінійні оператори

Лінійний оператор A приймає будь-який вектор у лінійному векторному просторі до вектора в цьому просторі\(A|V\rangle=|V'\rangle\) і задовольняє\[A(c_1|V_1\rangle+c_2|V_2\rangle)= c_1A|V_1\rangle+c_2A|V_2\rangle \tag{2.2.15}\]

з\(c_1\),\(c_2\) довільні складні константи.

Оператор ідентичності\(I\) є (очевидно!) визначається:\[ I|V\rangle=|V\rangle \;\; for \; all \; |V\rangle \tag{2.2.16}\]

Для n -вимірного векторного простору з ортонормальною основою\(|1\rangle,...,|n\rangle\), оскільки будь-який вектор у просторі може бути виражений як сума\(|V\rangle=\sum v_i|i\rangle\), лінійний оператор повністю визначається його дією на базисних векторах — це все, що нам потрібно знати. Легко знайти вираз для оператора ідентичності з точки зору бюстгальтерів і кетів.

Беручи внутрішній твір обох сторін рівняння\(|V\rangle=\sum v_i|i\rangle\) з бюстгальтером\(\langle i|\) дає\(\langle i|V\rangle=v_i\), так\[ |V\rangle=\sum v_i|i\rangle=\sum |i\rangle\langle i|V\rangle \tag{2.2.17}\]

Оскільки це вірно для будь-якого вектора в просторі, то випливає, що оператор ідентичності є просто\[ I=\sum_1^n |i\rangle\langle i| \tag{2.2.18}\]

Це важливий результат: він знову з'явиться у багатьох маскуваннях.

Щоб проаналізувати дію загального лінійного оператора\(A\), нам просто потрібно знати, як він діє на кожен базисний вектор. Починаючи з того\(A|1\rangle\), що це повинна бути деяка сума над базисними векторами, і оскільки вони ортонормальні, компонент у\(|i\rangle\) напрямку повинен бути справедливим\(\langle i|A|1\rangle\).

Тобто,\[ A|1\rangle=\sum_1^n |i\rangle\langle i|A|1\rangle=\sum_1^n A_{i1}|i\rangle\, ,\; writing\; \langle i|A|1\rangle =A_{i1} \tag{2.2.19}\]

Так що, якщо лінійний оператор діє на\(|V\rangle=\sum v_i|i\rangle\) дає\(|V'\rangle=\sum v_i'|i\rangle\), тобто\(A|V\rangle=|V'\rangle\), лінійність говорить нам, що\[ \sum v_i'|i\rangle=|V'\rangle=A|V\rangle=\sum v_j A|j\rangle= \sum_{i,j} v_j |i\rangle\langle i|A|j\rangle=\sum_{i,j} v_j A_{ij}|i\rangle \tag{2.2.20}\]

де на четвертому кроці ми просто вставили оператор ідентичності.

Оскільки всі ортогональні, коефіцієнт конкретного\(|i\rangle\) на лівій стороні рівняння повинен бути ідентичним з коефіцієнтом того ж\(|i\rangle\) на правій стороні.\(|i\rangle\) Тобто,\(v_i'=A_{ij}v_j\).

Тому оператор\(A\) просто еквівалентний множенню матриці:

\[\begin{pmatrix}v_1'\\ v_2'\\ .\\ .\\ v_n'\end{pmatrix}= \begin{pmatrix} \langle1|A|1\rangle &\langle1|A|2\rangle & .& .&\langle1|A|n\rangle\\ \langle2|A|1\rangle &\langle2|A|2\rangle & .& .& .\\ .& .& .& .& .\\ . & .& .& .& .\\ \langle n|A|1\rangle &\langle n|A|2\rangle & .& .&\langle n|A|n\rangle \end{pmatrix} \begin{pmatrix}v_1\\ v_2\\ .\\ .\\ v_n\end{pmatrix} \tag{2.2.21}\]

Очевидно, тоді застосування двох лінійних операторів один за одним еквівалентно послідовному множенню матриць - і, отже, оскільки матриці взагалі не комутують, а також не лінійні оператори. (Звичайно, якщо ми сподіваємося представити квантові змінні як лінійні оператори на векторному просторі, це має бути правдою - оператор імпульсу,\(p=-i\hbar d/dx\) безумовно, не їздить з x!)

Оператори проекції

Важливо зазначити, що лінійний оператор, що застосовується послідовно до членів ортонормальної основи, може дати новий набір векторів, які більше не охоплюють весь простір. Для прикладу лінійний оператор,\(|1\rangle\langle 1|\) застосований до будь-якого вектора у просторі, вибирає компонент вектора у\(|1\rangle\) напрямку. Це називається оператор проекції. Оператор\((|1\rangle\langle 1|+|2\rangle\langle 2|)\) проектує вектор на його компоненти в підпросторі\(|2\rangle\), що охоплюється\(|1\rangle\) векторами тощо - якщо ми продовжимо суму на всю основу, ми відновлюємо оператор ідентичності.

Вправа: довести, що матричне представлення оператора проекції\((|1\rangle\langle 1|+|2\rangle\langle 2|)\) має всі елементи нуль, крім перших двох діагональних елементів, які рівні одиниці.

Зворотного оператора до нетривіального оператора проекції бути не може, оскільки втрачається інформація про складові вектора перпендикулярно проектованому підпростору.

Сполучений оператор та ермітові матриці

Як ми вже обговорювали, якщо кет\(|V\rangle\) у n -вимірному просторі записаний як вектор-стовпчик з\(n\) (складними) компонентами, то відповідним бюстгальтером є вектор-рядок, який має як елементи комплексні сполучення елементів ket. \(\langle W|V\rangle=\langle V|W\rangle^*\)потім випливає автоматично зі стандартних правил множення матриці, а при\(|V\rangle\) множенні на комплексне число\(a\) отримати\(a|V\rangle\) (мається на увазі, що кожен елемент в стовпці чисел множиться на\(a\)) відповідний бюстгальтер переходить на\(\langle V|a^*=a^*\langle V|\).

Але припустимо, що замість того, щоб множити кет на число, ми оперуємо на ньому лінійним оператором. Що породжує паралельне перетворення серед бюстгальтерів? Іншими словами, якщо\(A|V\rangle=|V'\rangle\), який оператор відправляє бюстгальтер\(\langle V|\)\(\langle V'|\)? Він повинен бути лінійним оператором, тому що\(A\) є лінійним, тобто якщо під\(A\)\(|V_1\rangle \to |V_1'\rangle\)\(|V_3\rangle=|V_1\rangle +|V_2\rangle\),\(|V_2\rangle \to |V_2'\rangle\) а,\(A\)\(|V_3\rangle\) то під потрібно потрапити\(|V_3'\rangle=|V_1'\rangle +|V_2'\rangle\). Отже, під паралельне перетворення бюстгальтера ми повинні мати\(\langle V_1|\to \langle V_1'|\),\(\langle V_2|\to \langle V_2'|\) і\(\langle V_3|\to \langle V_3'|\), —перетворення бюстгальтера обов'язково також лінійне. Згадуючи, що бюстгальтер є n -елементним рядковим вектором, найзагальнішим лінійним перетворенням, що відправляє його в інший бюстгальтер, є\(n\times n\) матриця, що працює на бюстгальтері справа.

Цей оператор бюстгальтера називається суміжним\(A\), написаним\(A^{\dagger}\). Тобто кетка\(A|V\rangle\) має відповідний бюстгальтер\(\langle V|A^{\dagger}\). В ортонормальній основі, використовуючи позначення\(\langle Ai|\) для позначення бюстгальтера,\(\langle i|A^{\dagger}\) відповідного кету\(A|i\rangle=|Ai\rangle\), скажімо,\[ (A^{\dagger})_{ij}=\langle i|A^{\dagger}|j\rangle=\langle Ai|j\rangle=\langle j|Ai\rangle^*=A_{ji}^* \tag{2.2..22}\]

Таким чином, суміжний оператор - це сполучений комплекс транспонування.

Важливо: для добутку двох операторів (доведіть це!) ,\[ (AB)^{\dagger}=B^{\dagger}A^{\dagger} \tag{2.2..23}\]

Оператор, рівний його суміжному\(A=A^{\dagger}\) , називається Ермітовим. Як ми з'ясуємо в наступній лекції, ермітові оператори мають центральне значення в квантовій механіці. Оператором, рівним мінус його прилеглим\(A=-A^{\dagger}\),, є анти Ерміт (іноді називають косою ермітієвої). Ці два типи операторів по суті є узагальненням дійсного та уявного числа: будь-який оператор може бути виражений як сума ермітового оператора та анти ермітієвого оператора,\[ A=\frac{1}{2}(A+A^{\dagger})+\frac{1}{2}(A-A^{\dagger}) \tag{2.2.24}\]

Визначення суміжного природним чином поширюється на вектори і числа: суміжним кетом є відповідний бюстгальтер, суміжний числа - його складний сполучений. Це корисно мати на увазі, приймаючи суміжний оператор, який може бути частково побудований з векторів і чисел, таких як оператори проекційного типу. Сполучення добутку матриць, векторів і чисел є добутком суміжних в зворотному порядку. (Звичайно, для номерів порядок не має значення.)

Унітарні оператори

Оператор унітарний if\(U^{\dagger }U=1\). Це має на увазі перше, що\(U\) діючи на будь-якому векторі, дає вектор, що має таку ж норму, починаючи з нової норми\(\langle V|U^{\dagger }U|V\rangle=\langle V|V\rangle\). Крім того, внутрішні вироби зберігаються,\(\langle W|U^{\dagger }U|V\rangle=\langle W|V\rangle\). Тому при унітарному перетворенні початкова ортонормальна основа в просторі повинна перейти на іншу ортонормальну основу.

І навпаки, будь-яке перетворення, яке приймає одну ортонормальну основу в іншу, є унітарним перетворенням. Щоб побачити це, припустимо, що лінійне перетворення\(A\) посилає члени ортонормальної основи\((|1\rangle_1,|2\rangle_1,...,|n\rangle_1)\) в різну ортонормальну множини\((|1\rangle_2,|2\rangle_2,...,|n\rangle_2)\)\(A|1\rangle_1=|1\rangle_2\), так і т.д. тоді вектор\(|V\rangle= \sum v_i |i\rangle_1\) піде до\(|V'\rangle=A|V\rangle=\sum v_i |i\rangle_2\), що має однакову норму,\(\langle V'|V'\rangle= \langle V|V\rangle=\sum |v_i|^2\). Елемент матриці\(\langle W'|V'\rangle= \langle W|V\rangle=\sum w_i^*v_i\), але також\(\langle W'|V'\rangle=\langle W|A^{\dagger}A|V\rangle\). Тобто\(\langle W|V\rangle= \langle W|A^{\dagger}A|V\rangle\) для довільних кетів\(|V\rangle, \: |W\rangle\). Це можливо тільки в тому випадку\(A^{\dagger}A=1\), якщо,\(A\) так унітарно.

Унітарна операція дорівнює обертанню (можливо, поєднаному з відображенням) у просторі. Очевидно, оскільки\(U^{\dagger}U=1\), прилеглий\(U^{\dagger}\) обертає основу назад—це зворотна операція, а так\(UU^{\dagger}=1\) само, тобто\(U\) і\(U^{\dagger}\) коммутіруют.

Детермінанти

У цьому розділі ми розглядаємо детермінант матриці, функції, тісно пов'язаної з операторними властивостями матриці.

Почнемо з\(2\times2\) матриць:\[ A=\begin{pmatrix} a_{11} &a_{12} \\ a_{21} &a_{22} \end{pmatrix} \tag{2.2.25}\]

Визначник цієї матриці визначається:\[ \det A=|A|=a_{11}a_{22}-a_{12}a_{21} \tag{2.2.26}\]

Запис двох рядків матриці у вигляді векторів:\[ \vec a_1^R=(a_{11},a_{12}) \\ \vec a_2^R=(a_{21},a_{22}) \tag{2.2.27}\]

(\(R\)позначає рядок),\(\det A=\vec a_1^R \times \vec a_2^R\) це просто площа (з відповідним знаком) паралелограма, що має два вектори рядків як сусідні сторони:

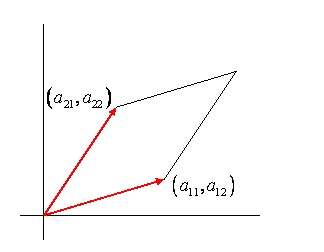
Це нуль, якщо два вектори паралельні (лінійно залежні) і не змінюються шляхом додавання кратного\(\vec a_2^R\) до\(\vec a_2^R\) (оскільки новий паралелограм має ту саму основу і таку ж висоту, як оригінал - перевірте це шляхом малювання).

Перейдемо до більш цікавого випадку\(3\times3\) матриць:\[ A=\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix} \tag{2.2.28}\]

Детермінант\(A\) визначається як\[ \det A=\varepsilon_{ijk}a_{1i}a_{2j}a_{3k} \tag{2.2.29}\]

де,\(\varepsilon_{ijk}=0\) якщо будь-які два рівні, +1\(ijk = 123, \; 231 \; or\; 312\) if (тобто парна перестановка 123) і —1, якщо\(ijk\) є непарною перестановкою 123. Повторні суфікси, звичайно, мають на увазі підсумовування тут.

Виписуючи це явно,\[ \det A= a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{11}a_{32}a_{23}-a_{21}a_{12}a_{33}-a_{31}a_{22}a_{13} \tag{2.2.30}\]

Так само, як і в двох вимірах, варто подивитися на цей вираз з точки зору векторів, що представляють рядки матриці\[ \vec a_1^R=(a_{11},a_{12},a_{13}) \\ \vec a_2^R=(a_{21},a_{22},a_{23}) \\ \vec a_3^R=(a_{31},a_{32},a_{33}) \tag{2.2.31}\]

так\[ A= \begin{pmatrix} \vec a_1^R\\ \vec a_2^R\\ \vec a_3^R \end{pmatrix} \: , \; and \; we \; see \; that \; \det A=(\vec a_1^R \times \vec a_2^R)\cdot \vec a_3^R \tag{2.2.32}\]

Це об'єм паралелопіда, утвореного трьома векторами, що є суміжними сторонами (зустріч в одному куті, початок).

Цей об'єм паралелепіпеда, звичайно, дорівнюватиме нулю, якщо три вектори лежать у площині, і він не змінюється, якщо до іншого з векторів додається кратний одному з векторів. Тобто визначник матриці не змінюється, якщо до іншого рядка додається кратний одному рядку. Це пояснюється тим, що детермінант лінійний в елементах одного ряду,\[ \det \begin{pmatrix} \vec a_1^R+\lambda\vec a_2^R \\ \vec a_2^R \\ \vec a_3^R \end{pmatrix}=\det \begin{pmatrix} \vec a_1^R\\ \vec a_2^R \\ \vec a_3^R \end{pmatrix} +\lambda\det \begin{pmatrix} \vec a_2^R\\ \vec a_2^R\\ \vec a_2^R \end{pmatrix} \tag{2.2.33}\]

і останній член дорівнює нулю, тому що два рядки однакові, тому потрійний векторний добуток зникає.

Більш загальний спосіб констатації цього, застосовний до більших детермінант, полягає в тому, що для визначника з двома однаковими рядками симетрія двох рядків разом з антисиметрією гарантує\(\varepsilon_{ijk}\), що члени в сумі всі скасовуються парами.

Оскільки визначник не змінюється шляхом додавання декількох кратних одному рядку до іншого, якщо рядки лінійно залежні, один рядок можна зробити однаково нульовим шляхом додавання правильних кратних інших рядків. Оскільки кожен член у виразі для детермінанта має один елемент з кожного рядка, визначник тоді буде однаково нульовим. Для тривимірного випадку лінійна залежність рядків означає, що відповідні вектори лежать в площині, а паралелепіпед - плоский.

Алгебраїчний аргумент легко узагальнюється до\(n\times n\) детермінантів: вони однаково нульові, якщо рядки лінійно залежні.

Узагальнення від\(3\times3\) до\(n\times n\) детермінант полягає в тому, що\(\det A=\varepsilon_{ijk}a_{1i}a_{2j}a_{3k}\) стає:

\[ \det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}...a_{np} \tag{2.2.34}\]

де\(ijk...p\) підсумовується по всіх перестановках\(132...n\), а\(\varepsilon\) символ дорівнює нулю, якщо будь-які два його суфікси рівні, +1 для парної перестановки і - 1 для непарної перестановки. (Примітка: будь-яка перестановка може бути записана як добуток свопів сусідів. Таке уявлення взагалі не є унікальним, але при заданій перестановці всі подібні уявлення матимуть або непарну кількість елементів, або парне число.)

Важливою теоремою є те, що для добутку двох матриць\(A\) детермінантою добутку є добуток детермінант,\(\det AB=\det A\times \det B\).\(B\) Це можна перевірити грубою силою для\(2\times2\) матриць, а доказ в загальному випадку можна знайти в будь-якій книзі з математичної фізики (наприклад, Байрон і Фуллер).

Також можна довести, що якщо рядки лінійно незалежні, визначник не може бути нулем.

(Ось доказ: візьміть\(n\times n\) матрицю з векторами\(n\) рядків лінійно незалежними. Тепер розглянемо складові цих векторів в\(n – 1\) розмірному підпросторі перпендикулярно\((1, 0, ... ,0)\). Ці\(n\) вектори, кожен з яких має лише\(n – 1\) компоненти, повинні бути лінійно залежними, оскільки їх більше, ніж розмірність простору. Таким чином, ми можемо взяти деяку комбінацію рядків нижче першого рядка і відняти його від першого рядка, щоб залишити перший рядок\((a, 0, 0, ... ,0)\), і не може бути нулем, так як у нас є матриця з\(n\) лінійно незалежних рядків. Потім ми можемо відняти кратні цього першого рядка з інших рядків, щоб отримати детермінант, що має нулі в першому стовпці під першим рядком. Тепер подивіться\(n – 1\) на\(n – 1\) визначник, на який потрібно помножити\(a\).

Його рядки повинні бути лінійно незалежними, оскільки ті з початкової матриці були. Тепер приступаємо до індукції.)

Щоб повернутися до трьох вимірів, зрозуміло з форми\[ \det A= a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{11}a_{32}a_{23}-a_{21}a_{12}a_{33}-a_{31}a_{22}a_{13} \tag{2.2.30}\]

що ми могли б однаково прийняти стовпці\(A\) як три вектори,\(A=(\vec a_1^C, \vec a_2^C, \vec a_3^C) \) в очевидному позначенні\(\det A=(\vec a_1^C \times \vec a_2^C)\cdot \vec a_3^C\), і лінійна залежність між стовпцями також забезпечить зникнення детермінанта - так, насправді, лінійна залежність стовпців забезпечує лінійну залежність рядів.

Це також узагальнює\(n\times n\): у визначенні детермінанта суфікс рядка фіксований\(\det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}...a_{np}\), а суфікс стовпця переходить над усіма допустимими перестановками, з відповідним знаком - але ті самі терміни будуть генеруватися, зберігаючи суфікси стовпців у числовому порядку та що дозволяє суфіксу рядка пройти перестановки.

Осторонь: Взаємні вектори решітки

Можливо, варто згадати про те, як обернене\(3\times 3\) матричного оператора можна розуміти в терміні векторів. Для множини лінійно незалежних векторів\((\vec a_1, \vec a_2, \vec a_3)\) зворотна множина\((\vec b_1, \vec b_2, \vec b_3)\) може бути визначена\[ \vec b_1 =\frac{\vec a_2\times \vec a_3}{\vec a_1\times \vec a_2 \cdot \vec a_3} \tag{2.2.35}\]

і очевидні циклічні визначення для двох інших взаємних векторів. Ми відразу бачимо, що\[\vec a_i\cdot \vec b_j =\delta_{ij} \tag{2.2.36}\]

з чого випливає, що зворотна матриця до\[ A=\begin{pmatrix} \vec a_1^R\\ \vec a_2^R \\ \vec a_3^R \end{pmatrix} \; is \; B=\begin{pmatrix}\vec b_1^C& \vec b_2^C& \vec b_3^C\end{pmatrix} \tag{2.2.37}\]

(Ці реципрокні вектори важливі, наприклад, в рентгенівській кристалографії. Якщо кристалічна решітка має певні атоми в позиціях\(n_1\vec a_1 +n_2\vec a_2+n_3\vec a_3\), де\(n_1, n_2, n_3\) цілі числа, то зворотні вектори - це сукупність нормалей до можливих площин атомів, і ці площини атомів є важливими елементами в дифракційному рентгенівському розсіянні.)

власні та власні значення

Якщо оператор, що\(A\) працює на ket,\(|V\rangle\) дає кратний одному і тому ж кету,\[ A|V\rangle =\lambda|V\rangle \tag{2.2.38}\]

то кажуть,\(|V\rangle\) що це власний (або, так само часто, власний вектор, або власний стан!) \(A\)з власним значенням\(\lambda\).

Власні та власні значення мають центральне значення в квантовій механіці: динамічні змінні є операторами, фізичне вимірювання динамічної змінної дає власне значення оператора і змушує систему в власний кінеток.

У цьому розділі ми покажемо, як знайти власні значення та відповідні власні ігенкети для оператора\(A\). Ми будемо використовувати позначення\(A|a_i\rangle =a_i|a_i\rangle\) для множини власних кісток\(|a_i\rangle\) з відповідними власними значеннями\(a_i\). (Очевидно, що в рівнянні власного значення тут суфікс\(i\) не підсумовується.)

Першим кроком у вирішенні\(A|V\rangle =\lambda|V\rangle\) є пошук дозволених власних значень\(a_i\).

Запис рівняння в матричному вигляді:\[ \begin{pmatrix} A_{11}-\lambda & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-\lambda &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-\lambda \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ .\\ .\\ v_n \end{pmatrix} =0 \tag{2.2.39}\]

Це рівняння насправді говорить нам, що стовпці\(A-\lambda I\) матриці лінійно залежать! Щоб переконатися в цьому, запишіть матрицю у вигляді вектора рядка, кожен елемент якого є одним з його стовпців, і рівняння стане\[ (\vec M_1^C,\vec M_2^C,...,\vec M_n^C) \begin{pmatrix} v_1\\ .\\ .\\ .\\ v_n \end{pmatrix}=0 \tag{2.2.40}\]

що можна сказати\[ v_1\vec M_1^C+v_2\vec M_2^C+...+v_n\vec M_n^C=0 \tag{2.2.41}\]

стовпці матриці дійсно є лінійно залежним множиною.

Ми знаємо, що означає, що детермінант матриці\(A-\lambda I\) дорівнює нулю,\[ \begin{vmatrix} A_{11}-\lambda & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-\lambda &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-\lambda \end{vmatrix}=0 \tag{2.2.42}\]

Оцінка детермінантного використання\(\det A=\varepsilon_{ijk...p}a_{1i}a_{2j}a_{3k}....a_{np}\) дає\(n^{th}\) порядок полінома в\(\lambda\) іноді званому характеристичному поліномі. Будь-поліном можна записати через його корені:\[ C(\lambda-a_1)(\lambda-a_2)....(\lambda-a_n)=0 \tag{2.2.43}\]

де в\(a_i\), коріння многочлена, і\(C\) є загальною константою, яка з огляду детермінанти ми можемо бачити бути\((-1)^n\). (Це коефіцієнт\(\lambda^n\).) Коріння поліномів (яких ми ще не знаємо) насправді є власними значеннями. Наприклад, покласти\(\lambda=a_1\) в матрицю\(\det (A-a_1I)=0\), що означає, що\((A-a_1I)|V\rangle=0\) має нетривіальне рішення\(|V\rangle\), а це наш власний вектор\(|a_1\rangle\).

Зверніть увагу, що діагональний член у визначнику\((A_{11}-\lambda)(A_{22}-\lambda)....(A_{nn}-\lambda)\) генерує провідні два порядку в\((-1)^n(\lambda^{n}-(A_{11}+...+A_{nn})\lambda^{n-1})\) многочлені (і деякі члени нижчого порядку теж). Прирівнюючи коефіцієнт\(\lambda^{n-1}\) 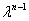тут до того, що в\((-1)^n(\lambda-a_1)(\lambda-a_2)....(\lambda-a_n)\),\[ \sum_{i=1}^n a_i=\sum_{i=1}^n A_{ii}= Tr A \tag{2.2.44}\]

\(\lambda=0\)Вставляючи як детермінантні, так і поліноміальні уявлення (іншими словами, прирівнюючи\(\lambda\) -незалежні члени),\[ \prod_{i=1}^n a_i=\det A \tag{2.2.45}\]

Таким чином, ми можемо знайти як суму, так і добуток власних значень безпосередньо з визначника, а для\(2\times 2\) матриці цього достатньо, щоб вирішити задачу.

Для чогось більшого метод полягає у вирішенні поліноміального рівняння,\(\det (A-\lambda I)=0\) щоб знайти набір власних значень, а потім використовувати їх для обчислення відповідних власних векторів. Робиться це по черзі.

Позначення першого знайденого власне значення як\(a_1\), відповідне рівняння для компонентів\(v_i\) v _i власне вектора\(|a_1\rangle\) дорівнює\[ \begin{pmatrix} A_{11}-a_1 & A_{12} &.&.& A_{1n} \\ A_{21} & A_{22}-a_1 &.&.&. \\ .&.&.&.&. \\ .&.&.&.&. \\ A_{n1} &.&.&.& A_{nn}-a_1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ .\\ .\\ v_n \end{pmatrix} =0 \tag{2.2.46}\]

Це виглядає як\(n\) рівняння для\(n\) чисел\(v_i\), але це не так: пам'ятайте, що рядки лінійно залежні, тому існують лише\(n–1\) незалежні рівняння. Однак цього достатньо, щоб визначити

співвідношення векторних компонентів\(v_1,...,v_n\), потім, нарешті, нормалізується власнийвектор. Потім процес повторюється для кожного власногозначення. (Додаткова обережність потрібна, якщо многочлен має збігаються коріння - ми обговоримо цей випадок пізніше.)

Власні значення та власні стани ермітових матриць

Для ермітієвої матриці легко встановити, що власні значення завжди дійсні. (Примітка: Основний постулат квантової механіки, розглянутий у наступній лекції, полягає в тому, що фізичні спостережувані представлені ермітовими операторами.) Беручи (в цьому розділі)\(A\) бути гермітом\(A=A^{\dagger}\), і маркування власних кісток власним значенням, тобто\[ A|a_1\rangle=a_1|a_1\rangle \tag{2.2.47}\]

внутрішнє виріб з бюстгальтером\(\langle a_1|\) дає\(\langle a_1|A|a_1\rangle=a_1\langle a_1|a_1\rangle\). А ось внутрішній добуток суміжного рівняння (запам'ятовуючи\(A=A^{\dagger}\))\[ \langle a_1|A=a_1^*\langle a_1| \tag{2.2.48}\]

з\(|a_1\rangle\)\(\langle a_1|A|a_1\rangle=a_1^*\langle a_1|a_1\rangle\) gives\(a_1=a_1^*\), так, і всі власні значення повинні бути реальними.

Вони, звичайно, не повинні бути різними - наприклад,\(I\) одинична матриця Ермітіана, і всі її власні значення, звичайно, 1. Але давайте спочатку розглянемо випадок, коли всі вони різні.

Легко показати, що власні кіетки, що належать до різних власних значень, є ортогональними.

Якщо\[ \begin{matrix} A|a_1\rangle=a_1|a_1\rangle \\ A|a_2\rangle=a_2|a_2\rangle \end{matrix} \tag{2.2.49}\]

візьміть суміжні першого рівняння, а потім внутрішнього добутку с\(|a_2\rangle\), і порівняйте його з внутрішнім добутком другого рівняння з\(\langle a_1|\):\[ \langle a_1|A|a_2\rangle=a_1\langle a_1|a_2\rangle=a_2\langle a_1|a_2\rangle \tag{2.2.50}\]

так що,\(\langle a_1|a_2\rangle=0\) якщо власні значення не рівні. (Якщо вони рівні, їх називають виродженими власними значеннями.)

Давайте спочатку розглянемо невироджений випадок:\(A\) має всі власні значення відмінні. Власні зв'язки\(A\), відповідним чином нормовані, утворюють ортонормальну основу в просторі.

Напишіть\[ |a_1\rangle=\begin{pmatrix} v_{11}\\ v_{21}\\ \vdots\\ v_{n1}\end{pmatrix},\; and\, consider\, the\, matrix\; V=\begin{pmatrix} v_{11}&v_{12}&\dots&v_{1n} \\ v_{21}&v_{22}&\dots&v_{2n}\\ \vdots&\vdots&\ddots&\vdots \\ v_{n1}&v_{n2}&\dots&v_{nn} \end{pmatrix}=\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix} \tag{2.2.51}\]

Зараз\[ AV=A\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix}=\begin{pmatrix}a_1|a_1\rangle & a_2|a_2\rangle & \dots & a_n|a_n\rangle \end{pmatrix} \tag{2.2.52}\]

так\[ V^{\dagger}AV=\begin{pmatrix} \langle a_1|\\ \langle a_2|\\ \vdots\\ \langle a_n|\end{pmatrix}\begin{pmatrix}a_1|a_1\rangle & a_2|a_2\rangle & \dots & a_n|a_n\rangle \end{pmatrix}=\begin{pmatrix} a_1&0&\dots&0 \\ 0&a_2&\dots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\dots&a_n \end{pmatrix} \tag{2.2.53}\]

Відзначимо також, що, очевидно,\(V\) є унітарним:\[ V^{\dagger}V=\begin{pmatrix} \langle a_1|\\ \langle a_2|\\ \vdots\\ \langle a_n|\end{pmatrix}\begin{pmatrix}|a_1\rangle & |a_2\rangle & \dots & |a_n\rangle \end{pmatrix}=\begin{pmatrix} 1&0&\dots&0 \\ 0&1&\dots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\dots&1\end{pmatrix} \tag{2.2.54}\]

Отже, встановлено, що для ермітієвої матриці з різними власними значеннями (невиродженим випадком) унітарна матриця, що\(V\) має стовпці, ідентичні\(A\) нормованим власним діагоналям\(A\),\(V^{\dagger}AV\) тобто діагональною. Крім того, його (діагональні) елементи дорівнюють відповідним власним значенням\(A\).

Інший спосіб сказати це полягає в тому, що унітарна матриця\(V\) - це перетворення від початкової ортонормальної основи в просторі до основи, утвореної з нормованих власних кісток\(A\).

Доказ того, що власні вектори ермітієвої матриці охоплюють простір

Тепер перейдемо до загального випадку: що робити, якщо деякі з власних значень\(A\) однакові? При цьому будь-яка лінійна їх комбінація також є власнимвектором з однаковим власним значенням. Припускаючи, що вони складають основу в підпросторі, процедура Грама Шмідта може бути використана для того, щоб зробити її ортонормальною, а отже, частиною ортонормальної основи всього простору.

Однак ми насправді не встановили, що власні вектори дійсно утворюють основу в виродженому підпросторі. Чи може бути, що (якщо взяти найпростіший випадок) два власні вектори для одного власного значення виявляються паралельними? Це насправді стосується деяких\(2\times2\) матриць - наприклад, нам потрібно довести\(\begin{pmatrix}1&1\\0&1\end{pmatrix}\), що це невірно для ермітієвих матриць, а також не є аналогічними твердженнями для вищих вироджених підпросторів.

Чітке уявлення наведено в Байроні і Фуллері, розділ 4.7. Ми слідуємо за ним тут. Процедура проводиться шляхом індукції з\(2\times2\) корпусу. Загальна\(2\times2\) ермітієва матриця має вигляд\[ \begin{pmatrix}a&b\\b^*&c\end{pmatrix} \tag{2.2.55}\]

де\(a\),\(c\) реальні. Легко перевірити, що якщо власні значення вироджені, ця матриця стає реальною кратною ідентичності, і тому тривіально має два ортонормальних власних вектора. Оскільки ми вже знаємо, що якщо власні значення\(2\times2\) ермітієвої матриці різні, то вона може бути діагоналізована унітарним перетворенням, утвореним з її ортонормальних власних векторів, ми встановили, що будь-яка матриця\(2\times2\) Ерміта може бути настільки діагоналізована.

Для здійснення процесу індукції ми тепер припустимо, що будь-яка матриця\((n-1)\times(n-1)\) Ерміта може бути діагоналізована унітарним перетворенням. Нам потрібно довести, що це означає, що це також вірно для\(n\times n\) ермітієвої матриці\(A\). (Нагадаємо, унітарне перетворення приймає одну повну ортонормальну основу на іншу. Якщо вона діагоналізує матрицю Ерміта, то новою основою обов'язково є набір ортонормалізованих власних векторів. Отже, якщо матрицю можна діагоналізувати, власні вектори охоплюють n -мірний простір.)

Виберіть власне значення, з\(a_1\)\(A\) нормованим власним вектором\(|a_1\rangle=(v_{11},v_{21},....,v_{n1})^T\). (Ми ставимо\(T\) для транспонування, щоб зберегти незручність заповнення сторінки кількома векторами стовпців.) Побудовано унітарний оператор,\(V\) зробивши його першим стовпчиком, а потім заповнюючи\(n-1\) іншими нормованими векторами для побудови n -мірної ортонормальної основи.\(|a_1\rangle\)

Тепер, оскільки\(A|a_1\rangle=a_1|a_1\rangle\), перший стовпець матриці\(AV\) буде якраз\(a_1|a_1\rangle\), а за рядками матриці\(V^{\dagger}=V^{-1}\) будуть\(\langle a_1|\) слідувати\(n-1\) нормовані вектори, ортогональні до нього, тому перший стовпець матриці\(V^{\dagger}AV\) буде \(a_1\)за якими йдуть нулі. Легко перевірити, що\(V^{\dagger}AV\) це Ермітіан, оскільки\(A\) є, тому його перший ряд також дорівнює нулю за першим діагональним терміном.

Це встановлює, що для\(n\times n\) ермітієвої матриці існує унітарне перетворення, щоб поставити її у вигляді:\[ V^{\dagger}AV=\begin{pmatrix} a_1 &0&.&.&0\\ 0& M_{22}&.&.&M_{2n} \\ 0&.&.&.&. \\ 0&.&.&.&. \\ 0 &M_{n2}&.&.& M_{nn} \end{pmatrix} \tag{2.2.56}\]

Але тепер ми можемо виконати друге унітарне перетворення в\((n-1)\times(n-1)\) підпросторі ортогональному\(|a_1\rangle\) (це, звичайно, залишає\(|a_1\rangle\) інваріантним), щоб завершити повну діагоналізацію - тобто існування\((n-1)\times(n-1)\) діагоналізації, плюс аргумент вище, гарантує існування \(n\times n\)діагоналізація: індукція завершена.

Діагоналізація матриці Ерміта

Як було розглянуто вище, матриця Ерміта є діагональною в ортонормальній основі своєї множини власних векторів:\(|a_1\rangle,|a_2\rangle,...,|a_n\rangle\), оскільки\[ \langle a_i|A|a_j\rangle=\langle a_i|a_j|a_j\rangle=a_j\langle a_i|a_j\rangle=a_j\delta_{ij} \tag{2.2.57}\]

Якщо нам задано матричні елементи\(A\) в якомусь іншому ортонормальному базисі, для його діагоналізації нам потрібно повернути від початкової ортонормальної основи до однієї, що складається з власних кісток\(A\).

Позначення початкової ортонормальної основи стандартним способом\[ |1\rangle=\begin{pmatrix} 1\\0\\0\\ \vdots\\0\end{pmatrix}, \; |2\rangle=\begin{pmatrix} 0\\1\\0\\ \vdots\\0\end{pmatrix}, \; |i\rangle=\begin{pmatrix} 0\\ \vdots\\ 1\\ \vdots\\0\end{pmatrix}... \; (1\, in\, i^{th}\, place\, down), \; |n\rangle=\begin{pmatrix} 0\\0\\0\\ \vdots\\1\end{pmatrix} \tag{2.2.58}\]

елементами матриці є\(A_{ij}=\langle i|A|j\rangle\).

Трансформація з однієї ортонормальної основи в іншу - це унітарне перетворення, про що говорилося вище, тому ми її пишемо\[ |V\rangle \to |V'\rangle=U|V\rangle \tag{2.2.59}\]

При цьому перетворенні елемент матриці\[ \langle W|A|V\rangle \to \langle W'|A|V'\rangle=\langle W|U^{\dagger}AU|V\rangle \tag{2.2.60}\]

Таким чином, ми можемо знайти відповідну матрицю перетворення,\(U\) вимагаючи, щоб\(U^{\dagger}AU\) бути діагоналлю відносно вихідного набору базисних векторів. (Трансформація оператора таким чином, залишаючи векторний простір в спокої, еквівалентно обертанню векторного простору і залишенню оператора в спокої. Звичайно, в системі з більш ніж одним оператором однакова трансформація повинна бути застосована до всіх операторів).

Насправді, так само, як ми обговорювали для невиродженого (різні власні значення) випадку, унітарна матриця, яка\(U\) нам потрібна, просто складається з нормованих власних кісток оператора\(A\),\[ U=(|a_1\rangle,|a_2\rangle,...,|a_n\rangle) \tag{2.2.61}\]

І це випливає, як до цього.\[ (U^{\dagger}AU)_{ij}=\langle a_i|a_j|a_j\rangle=\delta_{ij}a_j, \; a\, diagonal\, matrix. \tag{2.2.62}\]

(Повторні суфікси тут, звичайно, не підсумовуються.)

Якщо деякі власні значення однакові, процедура Грама Шмідта може знадобитися для створення ортогональної множини, як уже згадувалося раніше.

Функції матриць

Той же унітарний оператор\(U\), який діагоналізує матрицю Ерміта, також\(A\) буде діагоналізуватися\(A^2\), тому що\[ U^{-1}A^2U=U^{-1}AAU=U^{-1}AUU^{-1}AU \tag{2.2.63}\]

так\[ U^{\dagger}A^2U=\begin{pmatrix} a_1^2&0&0&.&0 \\ 0&a_2^2&0&.&0\\ 0&0&a_3^2&.&0 \\ .&.&.&.&. \\ 0&.&.&.&a_n^2\end{pmatrix} \tag{2.2.64}\]

Очевидно, що цей самий процес працює для будь-якої потужності\(A\), і формально для будь-якої функції\(A\) виражається як степеневий ряд, але, звичайно, слід враховувати властивості збіжності, і це стає складніше при переході від скінченних матриць до операторів на нескінченних просторах.

Поїздка на роботу Ермітієвих матриць

З вищесказаного, набір степенів ермітієвої матриці всі коммутують один з одним і мають загальний набір власних векторів (але не однакові власні значення, очевидно). Насправді неважко показати, що будь-які дві ермітові матриці, які комутують один з одним, мають однаковий набір власних векторів (після можливих перестановок Грама Шмідта в вироджених підпросторах).

Якщо дві\(n\times n\) ермітові матриці\(A\),\(B\) коммутіруют\(AB=BA\), тобто і\(A\) має невироджений набір власних векторів\(A|a_i\rangle=a_i|a_i\rangle\), то, тобто\(AB|a_i\rangle=BA|a_i\rangle=Ba_i|a_i\rangle=a_iB|a_i\rangle\),\(B|a_i\rangle\) є власним вектором\(A\) з власним значенням\(a_i\). Оскільки\(A\) є невиродженим,\(B|a_i\rangle\) має бути кілька кратних\(|a_i\rangle\), і ми робимо висновок\(A\), що,\(B\) мають однаковий набір власних векторів.

Тепер припустимо,\(A\) що вироджується, і розглянемо\(m\times m\) підпростір,\(S_{a_i}\) що охоплюється власними\(|a_i,1\rangle,\; |a_i,2\rangle,...\) векторами,\(A\) що мають власне значення\(a_i\). Застосовуючи аргумент в пункті вище, також\(B|a_i,1\rangle,\; B|a_i,2\rangle,...\) має лежати в цьому підпросторі. Тому, якщо ми трансформуємо\(B\) з тим самим унітарним перетворенням\(A\), що діагонально, взагалі не\(B\) буде діагоналлю в підпросторі\(S_{a_i}\), але це буде те, що називається блоковою діагоналлю, в тому, що якщо\(B\) працює на будь-якому векторі в\(S_{a_i}\) ньому дає вектор в\(S_{a_i}\).

\(B\)можна записати у вигляді двох діагональних блоків: один\(m\times m\)\((n-m)\times (n-m)\), один, з нулями поза цими діагональними блоками, наприклад, для\(m=2,\; n=5\):\[ \begin{pmatrix} b_{11}&b_{12}&0&0&0 \\ b_{21}&b_{22}&0&0&0 \\ 0&0&b_{33}&b_{34}&b_{35} \\ 0&0&b_{43}&b_{44}&b_{45} \\ 0&0&b_{53}&b_{54}&b_{55} \end{pmatrix} \tag{2.2.65}\]

І, по суті, якщо є тільки одне вироджене власне значення, то другий блок буде мати тільки ненульові члени по діагоналі:\[ \begin{pmatrix} b_{11}&b_{12}&0&0&0 \\ b_{21}&b_{22}&0&0&0 \\ 0&0&b_3&0&0 \\ 0&0&0&b_4&0 \\ 0&0&0&0&b_5 \end{pmatrix} \tag{2.2.65}\]

\(B\)отже діє на двох підпросторах: один m -мірний, один (n - m) -вимірний, незалежно —вектор повністю в одному підпросторі залишається там.

Це означає, що ми можемо завершити діагоналізацію\(B\) унітарним оператором, який працює лише на\(m\times m\) блоці\(S_{a_i}\). Такий оператор також вплине на власні вектори\(A\), але це не має значення, тому що всі вектори в цьому підпросторі є власними векторами\(A\) з однаковим власним значенням, тому, що стосується\(A\), ми можемо вибрати будь-яку ортонормальну основу, яка нам подобається - базисні вектори все одно будуть бути власними векторами.

Це встановлює, що будь-які дві комутуючі ермітієві матриці можуть бути діагональні одночасно. Очевидно, що це ніколи не може бути вірним для некомутаційних матриць, оскільки всі діагональні матриці комутують.

Діагоналізація унітарної матриці

Будь-яка унітарна матриця може бути діагональна шляхом унітарного перетворення. Щоб переконатися в цьому, нагадаємо, що будь-яку матрицю\(M\) можна записати як суму ермітієвої матриці і анти ермітієвої матриці,\[ M=\frac{M+M^{\dagger}}{2}+\frac{M-M^{\dagger}}{2}=A+iB \tag{2.2.66}\]

де\(A,\; B\) обидва - Ерміціанські. Це матричний аналог запису довільного комплексного числа у вигляді суми дійсної і уявної частин.

Якщо\(A,\; B\) комутують, то вони можуть бути одночасно діагональні (див. Попередній розділ), а значить,\(M\) можуть бути діагональними. Тепер, якщо унітарна матриця виражена в такому вигляді\(U=A+iB\) з\(A,\; B\) Ермітіаном, з\(UU^{\dagger}=U^{\dagger}U=1\) цього легко випливає\(A,\; B\) коммутіруют, тому будь-яка унітарна матриця\(U\) може бути діагоналізована унітарним перетворенням. Більш загально, якщо матриця\(M\) комутується зі своїм суміжним\(M^{\dagger}\), її можна діагоналізувати.

(Примітка: діагональ неможлива,\(M\) якщо обидва не будуть\(A,\; B\) одночасно діагоналізовані. Це випливає з\(U^{\dagger}AU,\; U^{\dagger}iBU\) того, що Ерміт і антиерміт для будь-якого унітарного оператора\(U\), тому їх позадіагональні елементи не можуть скасувати один одного, всі вони повинні бути нульовими, якщо М був діагональний\(U\), і в цьому випадку дві\(U^{\dagger}AU,\; U^{\dagger}iBU\) перетворені матриці діагональні, тому їздити на роботу, і так роблять оригінальні матриці\(A,\; B\).)

Варто подивитися на конкретному прикладі, просте обертання однієї ортонормальної основи в іншу в трьох вимірах. Очевидно, що вісь через початок, навколо якої обертається основа, є власнимвектором перетворення. Менш зрозуміло, якими можуть бути інші два власні вектори - або, що еквівалентно, які власні вектори відповідають двовимірному обертанню базису в площині? Спосіб дізнатися - записати матрицю і діагоналізувати її.

Матриця\[ U(\theta)=\begin{pmatrix} \cos \theta &\sin \theta\\ -\sin \theta &\cos \theta\end{pmatrix} \tag{2.2.67}\]

Зверніть увагу, що детермінант дорівнює одиниці. Власні значення задаються розв'язуванням\[ \begin{vmatrix} \cos \theta -\lambda &\sin \theta\\ -\sin \theta &\cos \theta -\lambda\end{vmatrix}=0\; to\, give\; \lambda=e^{\pm i\theta} \tag{2.2.68}\]

Відповідні власні вектори задовольняють

\[ \begin{pmatrix} \cos \theta &\sin \theta\\ -\sin \theta &\cos \theta\end{pmatrix}\dbinom{u_1^{\pm}}{u_2^{\pm}}=e^{\pm i\theta}\dbinom{u_1^{\pm}}{u_2^{\pm}} \tag{2.2.69}\]

Нормованими власними векторами є:\[ \dbinom{u_1^{\pm}}{u_2^{\pm}}=\frac{1}{\sqrt{2}}\dbinom{1}{\pm i} \tag{2.2.70}\]

Зауважимо, що, на відміну від ермітієвої матриці, власні значення унітарної матриці не обов'язково повинні бути дійсними. Насправді, з\(U^{\dagger}U=1\), затиснутий між бюстгальтером і кетом з власним вектором, ми бачимо, що будь-яке власне значення унітарної матриці повинно мати модуль одиниці - це комплексне число на одиничному колі. Озираючись назад, ми повинні були зрозуміти, що одне власне значення двовимірного обертання повинно бути\(e^{i\theta}\), добуток двох двовимірних обертань дається додаванням кутів повороту, а обертання через\(\pi\) змінює всі знаки, так має власне значення\(-1\). Зауважте, що власний вектор сам по собі не залежить від кута обертання - обертання всі комутують, тому вони повинні мати спільні власні вектори. Послідовні оператори обертання, застосовані до плюсового власного вектора, додають свої кути, при застосуванні до мінус власного вектора всі кути віднімаються.

Дописувач

• Template:ContribFowler