9.1: Поточний вектор
- Page ID
- 77240
Цілі навчання
- Поясніть збереження заряду
Струм як потік заряджених частинок
Найбільш фундаментальними законами фізики є закони збереження, які говорять нам про те, що ми не можемо створювати або знищувати «речі», де «речі» можуть означати такі величини, як електричний заряд або енергетичний імпульс. Оскільки заряд є інваріантом Лоренца, це простий приклад для початку. Оскільки заряд інваріантний, ми можемо також уявити, що щільність заряду\(ρ\) була інваріантною. Але це не так, по суті тому, що просторовий (\(3\)-мірний) об'єм не є інваріантним; у\(3 + 1\) вимірах лише чотиривимірний об'єм є інваріантним. Наприклад, припустимо, що у нас є ізолятор у формі куба, при цьому заряд розподілений рівномірно по всьому ньому відповідно до спостерігача\(o_1\) в спокої щодо куба. Потім в кадрі, що\(o_2\) рухається щодо куба, паралельно одній з його осей, куб стає укороченим скороченням довжини, а його обсяг зменшується в коефіцієнт\(1/γ\). Результатом є те, що щільність заряду в\(o_2\) більша в рази\(γ\).
Це означає, що знання щільності заряду\(ρ\) в одному кадрі недостатньо для визначення щільності заряду в іншому кадрі. У прикладі куба достатньо було б знання вектора\(J = ρ_0 v\), де\(ρ_0\) щільність заряду в кадрі спокою куба, і\(v\) вектор швидкості куба. \(J\), званий вектором струму, перетворюється як релятивістський вектор через властивості трансформації двох факторів, які його визначають. Швидкість\(v\) є вектором (перетин 3.5). Коефіцієнт\(ρ_0\) є інваріантним, так як він в свою чергу розпадається на заряд, розділений за обсягом спокою. Заряд - це інваріант, і всі спостерігачі сходяться на думці про те, який обсяг буде мати куб у своєму кадрі відпочинку.
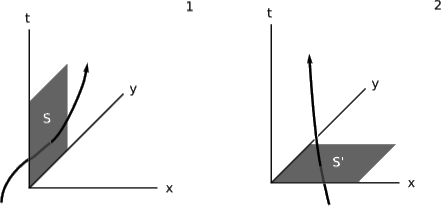
\(J\)може бути виражена в координатах Мінковського як\((ρ, J^x, J^y, J^z)\), де\(ρ\) щільність заряду і, наприклад,\(J^x\) щільність електричного струму в\(x\) напрямку. Припустимо, ми визначаємо три поверхні,\(S\) показані на малюнку\(\PageIndex{1}\) (1), що складається з безлічі подій з\((t, 0, y, z)\) такими координатами\(0 ≤ t ≤ 1\), що\(0 ≤ y ≤ 1\), і\(0 ≤ z ≤ 1\). Деякі заряджені частинки мають світові лінії, які перетинають цю поверхню, проходячи через неї або в позитивному\(x\) напрямку, або в негативному\(x\) напрямку (яке ми вважаємо транспортом негативного заряду). \(S\)має трьохтомний\(V\). Якщо скласти загальний транспорт заряду\(∆q\) по цій поверхні і розділити на\(V\), то отримаємо середнє значення\(J^x\). Якщо ми дозволимо\(S\) скорочуватися до менших і менших трьох поверхонь\((0, 0, 0, 0)\), що оточують подію, то ми отримаємо значення\(J^x\) в цій точці,\(lim_{V\to 0} \frac{\Delta q}{V}\). Іншими словами,\(J^x\) вимірює щільність потоку заряду, який проходить\(S\). Звичайно, цей опис з точки зору ліміту має на увазі велику кількість нарахувань, а не тільки один, як на малюнку\(\PageIndex{1}\).
Ви можете виписати аналогічне визначення для\(J^t\), використовуючи поверхню одночасності для like\(S'\), цифра\(\PageIndex{1}\) (2), і ви побачите, що вона виражає щільність заряду\(ρ\). При цьому\(S'\) являє собою момент у часі, а потік через\(S'\) означає, що заряди перетинають поріг з минулого в майбутнє.
Наш аргумент, який\(J\) трансформувався як вектор, базувався на випадку, коли всі заряджені частинки мали однаковий вектор швидкості, але наведене вище опис з точки зору потоку заряду усувало будь-яке обговорення швидкості. Це правда, але менш очевидно, що\(J\) описане таким чином також перетворюється як вектор, навіть у випадках, коли заряджені частинки не всі мають паралельні світові лінії. Вектор струму є джерелом електричного і магнітного полів. Примітно, що ніяке макроскопічне електричне вимірювання не здатне виявити що-небудь більш детальне про рух зарядів, ніж усереднена інформація, надана\(J\).
Приклад\(\PageIndex{1}\): Boosting a solenoid
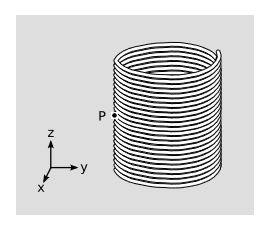
\(\PageIndex{2}\)На малюнку зображений соленоїд, в стані спокою, намотаний з мідного дроту. У точці\(P\) ми будуємо прямокутну амперійську петлю в\(yz\) площині, яка має правий край всередині соленоїда, а лівий - зовні. Закон Ампера,
\[\int B\cdot ds = \left ( \frac{4\pi k}{c^2} \right )l\]
то говорить нам, що щільність струму\(J_x\) викликає різницю між зовнішнім полем\(B_z = 0\) і внутрішнім полем\(B_z = \left ( \frac{4\pi k}{c^2} \right )J_x \Delta y\), де\(∆y\) товщина соленоїда. Є дві речі, які ми можемо отримати від цього результату, обидві вони нетривіальні.
По-перше, поле залежить тільки від щільності струму, а не від будь-якої інформації про деталі руху електронів в міді. Рух електронів є швидким і дуже випадковим, але все, що сприяє,\(J_x\) - це повільна швидкість дрейфу, як правило\(∼ 1\: cm/s\), накладається на випадковість. Це точно і зовсім не очевидно. Наприклад, сумарний імпульс електронів дійсно залежить від випадкової частини їх руху, тому що\(p_x = mγv_x\) має коефіцієнт\(γ\) в ньому.
По-друге, ми можемо використовувати властивості перетворення вектора струму, щоб знайти поле цього соленоїда в кадрі, збільшеному вздовж його осі. Це така ситуація, яка природно виникла б, наприклад, в електродвигуні, ротор якого містить електромагніт. Трансформація Лоренца в\(z\) напрямку не змінює\(x\) компонент вектора і не змінюється\(∆y\), так\(B_z\) само як і в обох кадрах. Це нетривіально як в тому сенсі, що важко було б з'ясувати грубою силою, так і в тому сенсі, що поля не повинні бути однаковими в різних системах відліку - наприклад, поштовх у\(y\) напрямку\(x\) або змінив би результат.
Приклад\(\PageIndex{2}\): A wire
У твердому провіднику, такому як мідний дріт, ми маємо два типи зарядів, протони та електрони. Протони знаходяться в стані спокою в лабораторному кадрі\(o\), з щільністю заряду\(ρ_p\) та щільністю струму
\[J_p = (ρ_p, 0, 0, 0) \]
в координатах Мінковського. Рух електронів ускладнюється. Деякі електрони пов'язані з певним атомом, але все ще рухаються з релятивістськими швидкостями всередині своїх атомів. Інші демонструють сильний тепловий рух, який дуже майже, але не зовсім, середній до нуля, коли є струм, виміряний амперметром. Для простоти розглядаємо всі електрони (як зв'язані, так і рухливі) як єдину щільність заряду\(ρ_e\). Нехай середня швидкість електронів, відома як швидкість їх дрейфу, буде\(v\) в\(x\) напрямку. Потім в кадрі\(o'\) рухаючись разом зі швидкістю дрейфу ми маємо
\[J_{e}^{'} = (\rho _{e}^{'}, 0, 0, 0)\]
який під час перетворення Лоренца назад в лабораторний кадр стає
\[J_{e} = (\rho _{e}^{'}\gamma , \rho _{e}^{'}V\gamma , 0, 0)\]
Додавши два поточних вектора, ми маємо загальний струм у лабораторному кадрі
\[J = (\rho _p + \rho _{e}^{'}\gamma , \rho _{e}^{'}V\gamma , 0, 0)\]
Провід електрично нейтральний в цій рамці, так що\(\rho _p + \rho _{e}^{'}\gamma =0\). Так як\(ρ_p\) є нерухомою властивістю дроту, виражаємо\(\rho _{e}^{'}\) в плані його як\(ρ_p/γ\). Усунення\(\rho _{e}^{'}\) дає
\[J = (0, -ρ_pV, 0, 0)\]
Оскільки\(γ\) фактори скасовані, ми виявляємо, що струм точно пропорційний швидкості дрейфу. Геометрично ми додали два вектори, схожі на час, і отримали пробіл; це можливо, тому що один з тимчасових векторів був спрямований на майбутнє, а інший спрямований на минуле.
Збереження заряду
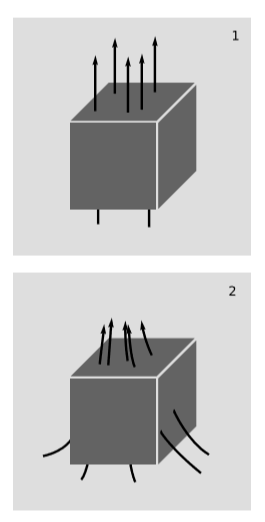
Збереження заряду може бути виражено елегантно в плані\(J\). Щільність заряду - це тимчасова складова\(J^t\). Якщо ця щільність заряду поблизу певної точки, наприклад, збільшується, то це може бути тому, що збереження заряду було порушено, як на малюнку\(\PageIndex{3}\) (1). У цьому прикладі більше світових ліній з'являється у майбутньому у верхній частині чотирикуба, ніж увійшло через дно в минулому. Деякий процес всередині куба створює заряд. У межі, де куб зроблений дуже малим, це буде вимірюватися значенням\(\frac{\partial J^t}{\partial t}\), яке було більше нуля.
Але експерименти ніколи не виявляли жодного порушення збереження заряду, тому якщо з верхньої (майбутньої) сторони куба виходить більше заряду, ніж прийшло знизу (минулого), то більш імовірне пояснення полягає в тому, що заряди не всі знаходяться в стані спокою, як на малюнку\(\PageIndex{3}\) (1), а рухаються, фігура\(\PageIndex{3}\) (2), і був чистий потік з сусідніх областей космосу. Ми повинні знайти це відображення в просторових компонентах\(J^x\),\(J^y\) і\(J^z\). Більш того, якби ці просторові компоненти були все постійними, то будь-яка задана область простору мала б стільки ж струму, що протікає в неї з одного боку, як і з іншого. Тому нам потрібно мати деякі ненульові часткові похідні, такі як\(\frac{\partial J^x}{\partial x}\). Наприклад, цифра\(\PageIndex{3}\) (2) має позитивний\(J^x\) зліва і негативний\(J^x\) справа, так\(\frac{\partial J^x}{\partial x} < 0\). Збереження заряду виражається простим рівнянням\(\frac{\partial J^{\lambda }}{\partial x^{\lambda }} = 0\). Виписуючи мається на увазі суму понад\(λ\), це говорить про те, що
\[\frac{\partial J^t}{\partial t} + \frac{\partial J^x}{\partial x} + \frac{\partial J^y}{\partial y} + \frac{\partial J^z}{\partial z} = 0\]
з неявною сумою над індексом\(λ\). Якщо ви взяли векторне обчислення, ви розпізнаєте оператор, до якого застосовується,\(J\) як чотиривимірне узагальнення розбіжності. Це рівняння збереження заряду дійсне незалежно від системи координат, тому його також можна переписати в абстрактних позначеннях індексу як
\[\frac{\partial J^a}{\partial x^a} = 0\]
Приклад\(\PageIndex{3}\): Conservation of charge in a solenoid
У соленоїді ми маємо заряд, що циркулює з деякою швидкістю дрейфу\(v\). Ігноруючи протони та адаптуючи відповідний вираз з прикладу\(\PageIndex{2}\) до випадку кругового, а не лінійного руху, ми могли б мати для внеску електронів у струм щось у формі
\[J = p(1, -qy, qx, 0),\]
де\(p = γv\) і\(q\) залежить від\(v\) і від радіуса соленоїда. Збереженням заряду задовольняється, тому що кожен з чотирьох членів в рівнянні
\[\frac{\partial J^t}{\partial t} + \frac{\partial J^x}{\partial x} + \frac{\partial J^y}{\partial y} + \frac{\partial J^z}{\partial z} = 0\]
зникає індивідуально.
