15.3: Рівняння руху

Спочатку розглянемо рух астероїда під гравітаційним впливом одного тільки Сонця, ігноруючи збурень від інших планет. Ми приймаємо масу Сонця рівною M, а масу астероїда - m. Сила на астероїді − і, звичайно, за третім законом Ньютона сила на Сонце - є\( \frac{G M m}{r^{2}}\), де r - відстань між двома тілами. Ці два тіла, звичайно, рухаються навколо свого загального центру маси, який, у випадку астероїда, знаходиться дуже близько до центру Сонця.

Прискорення астероїда до центру маси є\(\frac{G M}{r^{2}}\), і прискорення Сонця до центру маси є\(\frac{G m}{r^{2}}\). Якщо ми називаємо рух Сонця як походження, ми бачимо, що прискорення астероїда до Сонця є\( \frac{G(M+m)}{r^{2}}\). У векторній формі ми можемо написати це як

\[\ddot{\mathbf{r}}=-\frac{G(M+m)}{r^{3}} \mathbf{r},\]

де r - вектор, спрямований від Сонця до астероїда, з геліоцентричними прямокутними складовими (x, y, z). Ці геліоцентричні координати можуть бути або екліптичними координатами, для яких ми досі використовували символи (X, Y, Z); або вони можуть бути екваторіальними координатами, для яких ми досі використовували символи (, η,). Символи (x, y, z) будуть зрозумілі тут, щоб посилатися на будь-який, на нашу зручність. Більш імовірно, що у нас будуть доступні екваторіальні, а не екліптичні координати. Косинуси напряму r є\( \left(\frac{x}{r}, \frac{y}{r}, \frac{z}{r}\right)\), а отже, прямокутні складові Рівняння 15.3.1

\[ \ddot{x}=-\frac{G(M+m)}{r^{3}} x\]

\[ \ddot{y} =-\frac{G(M+m)}{r^{3}} y\]

\[\ddot{z} =-\frac{G(M+m)}{r^{3}} z\]

Це рівняння руху астероїда по відношенню до Сонця як походження. \(x, y, z, r\left(=\sqrt{x^{2}+y^{2}+z^{2}}\right)\)Величини - це, звичайно, функції часу. Розв'язок цих рівнянь описує еліптичні (або інші конічні перерізи) орбіти астероїда та всі інші властивості, які ми обговорювали в попередніх розділах.

Якщо ми використовуємо екліптичні координати (X, Y, Z), вісь X спрямована в сторону Першої точки Овна, вісь Y спрямована уздовж напрямку наростаючої екліптичної довготи, а вісь Z спрямована в бік північного полюса екліптики.

Якщо ми використовуємо екваторіальні координати (θ, η,), то -вісь спрямована до Першої точки Овна, η -вісь спрямована уздовж напрямку 6 годин прямого підйому, а -вісь спрямована до північного небесного полюса. Земля буде на осі X- або у вересні (не в березні).

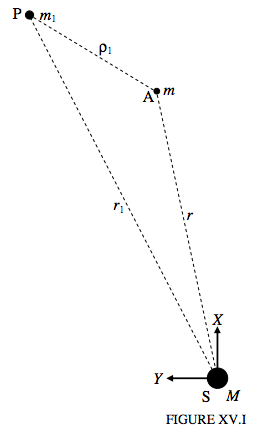
Тепер введемо третє тіло, збурену планету, таку як, мабуть, Юпітер. Ми припустимо, що його маса дорівнює m ₁, що його відстань від Сонця дорівнює r ₁, а відстань від астероїда - ρ ₁ (див. Рис. XV.I, на якому S - Сонце, А - астероїд, а P - збурена планета). Це тепер задача з трьох тіл, і загальне рішення з точки зору алгебраїчних функцій неможливо, і його доводиться вирішувати числовими обчисленнями.

Окрім прискорень астероїда до Сонця та Сонця до астероїда, описаних на сторінці 3, використовуваних при розробці рівнянь 15.3.1-4, тепер нам доведеться також розглянути прискорення астероїда та Сонця до збуреної планети, як зазначено на малюнку XV.II.

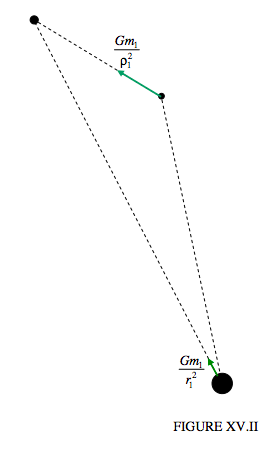
Х-складовими є\( \frac{G m_{1}}{\rho_{1}^{2}} \times \frac{x_{1}-x}{\rho_{1}}\) і\( \frac{G m_{1}}{r_{1}^{2}} \times \frac{x_{1}}{r_{1}}\), отже, додаткове прискорення A, відносно Сонця, у напрямку X є\( G m_{1}\left(\frac{x_{1}-x}{\rho_{1}^{3}}-\frac{x_{1}}{r_{1}^{3}}\right)\), і це тепер має бути додано до правого боку Рівняння 15.3.2:

\[ \ddot{x}=-\frac{G(M+m)}{r^{3}} x+G m_{1}\left(\frac{x_{1}-x}{\rho_{1}^{3}}-\frac{x_{1}}{r_{1}^{3}}\right)\]

Ні G, ні M не відомі з великою точністю, але продукт GM відомий з дуже великою точністю. Дійсно, в обчислювальній практиці ми використовуємо константу Гауса\( k=\sqrt{\frac{G M}{a_{0}}}\), де ₀ - астрономічна одиниця довжини. Ця константа має розмірність T ⁻¹ і дорівнює кутовій швидкості частинки мізерно малої маси на круговій орбіті радіусом 1 ау навколо Сонця, що становить 0,017 202 098 95 радіанів на середню сонячну добу. Тому в обчислювальній практиці рівняння 15.3.5 зазвичай пишеться як

\[ \ddot{x}=-\frac{k^{2}(1+m)}{r^{3}} x+k^{2} m_{1}\left(\frac{x_{1}-x}{\rho_{1}^{3}}-\frac{x_{1}}{r_{1}^{3}}\right),\]

в якому одиницями маси, довжини і часу є, відповідно, сонячна маса, астрономічна одиниця і середній сонячний день. Нагадаємо, що m - маса астероїда, орбіту якого ми обчислюємо, а m ₁ - маса збуреної планети, і що походження координат - це центр Сонця. Подібні рівняння застосовуються до y - і z -компонентів:

\[ \ddot{y}=-\frac{k^{2}(1+m)}{r^{3}} y+k^{2} m_{1}\left(\frac{y_{1}-y}{\rho_{1}^{3}}-\frac{y_{1}}{r_{1}^{3}}\right)\]

\[\ddot{z}=-\frac{k^{2}(1+m)}{r^{3}} z+k^{2} m_{1}\left(\frac{z_{1}-z}{\rho_{1}^{3}}-\frac{z_{1}}{r_{1}^{3}}\right)\]

Якщо додати збурень від усіх основних планет від Меркурія (М) до Нептуна (N), ці Рівняння стануть, звичайно,

\[ \ddot{x}=-\frac{k^{2}(1+m)}{r^{3}} x+k^{2} \sum_{i=M}^{N} m_{i}\left(\frac{x_{i}-x}{\rho_{i}^{3}}-\frac{x_{i}}{r_{i}^{3}}\right)\]

і подібні рівняння в y і z.

У випадку з астероїдом або кометою може бути допустимо знехтувати m в цьому Рівнянні (тобто встановити m = 0), але не, звичайно, m ₁. Ми зробимо це тут, так рівняння руху в х стає

\[\ddot{x}=-k^{2} \frac{x}{r^{3}}+k^{2} \sum_{i=\mathrm{M}}^{\mathrm{N}} m_{i}\left(\frac{x_{i}-x}{\rho_{i}^{3}}-\frac{x_{i}}{r_{i}^{3}}\right),\]

з подібними рівняннями у та z.

X, x _i, ρ _i, r _i тощо - це числові дані, які повинні надаватися незалежними обчисленнями (підпрограмами) для всіх планет. Як зазначено в кінці попереднього розділу, ми припускаємо, що у нас є підпрограми в нашій програмі, які ми можемо закликати обчислити ці дані в будь-яку дату. Ми також зазначили, що рівняння руху дійсні для екліптичних або екваторіальних координат, хоча координати планет, швидше за все, будуть доступні екваторіальні, а не екліптичні координати. Всі вони є функціями часу, так що, по суті, доводиться розробляти числові методи інтеграції рівнянь виду, де f (t) - це не алгебраїчний вираз, а скоріше таблиця числових значень.

\[\ddot{x}=f(t)\]

Тобто

\[\frac{d \dot{x}}{d t}=f(t).\]

Ми припускаємо, що ми знаємо x & в епоху оскуляції. Тоді ми можемо знайти\(\dot{x}\) в будь-яку наступну дату будь-якою стандартною технікою числового інтегрування, наприклад, правилами Сімпсона чи Веддла, або квадратурою Гаусса, або процесом Рунге-Кутти. Таким чином, тепер у нас є таблиця\(\dot{x}\) як функція часу:

\[\dot{x}=g(t)\]

Тобто

\[\frac{d x}{d t}=g(t)\]

Ми інтегруємо вдруге, поки не дійдемо як до x, так і\(\dot{x}\) в деяку наступну епоху оскуляції (можливо, 200, або 40, днів у майбутнє). Повторіть з y і z компонентів, так що ми в кінцевому підсумку є новий набір\((x, y, z, \dot{x}, \dot{y}, \dot{z})\) для більш пізньої епохи, а отже, і з a, e, i, Ω, ω, T.