10.2: Елементи еліптичної орбіти

Last updated
Save as PDF

Page ID: 77835

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Шість чисел необхідні і достатні для опису еліптичної орбіти в трьох вимірах. До них відносяться чотири (\(a\),\(ω\) і\(T\))\(e\), які ми описали в розділі 9.9 для двовимірного випадку. Два додаткових кута, на які будуть дані символи\(i\) і\(Ω\), знадобляться для завершення опису орбіти в 3-му просторі.

Шість елементів еліптичної орбіти, отже, такі.

\(a\)пів-велика вісь, зазвичай виражається в астрономічних одиницях (\(\text{AU}\)).
\(e\)
\(i\)ексцентриситет
\(Ω\) нахил довгота
\(ω\) висхідного вузла аргумент
\(T\) перигелія час проходження перигелію

Три кути\(i\),\(Ω\) і завжди\(ω\) повинні бути віднесені до рівнодення і екватора заявленої епохи. Наприклад, в даний час їх зазвичай відносять до середнього рівнодення і екватора\(\text{J2000.0}\). Значення трьох кутів пояснюються на малюнку\(\text{X.1}\) та наступних параграфах.

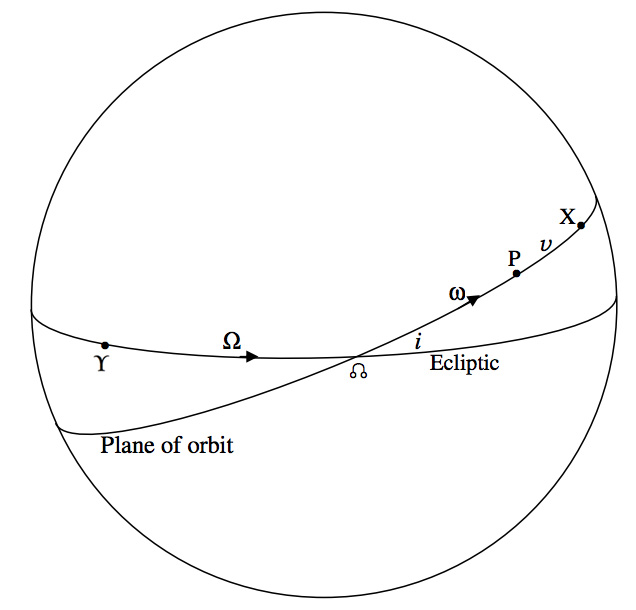
Малюнок 10.1.jpg
\(\text{FIGURE X.1}\)

На малюнку\(\text{X.1}\) я намалював небесну сферу, зосереджену на Сонці. Два великі кола покликані представляти площину орбіти Землі (тобто екліптику) і площину орбіти планети - (тобто не саму орбіту, а її проекцію на небесну сферу). Точка\(\text{P}\) являє собою проекцію перигеліонной точки орбіти на небесну сферу, а точка\(\text{X}\) - проекція планети на небесну сферу в якийсь час. Дві точки, де перетинаються площина екліптики і площина орбіти планети, називаються вузлами, а відмічена точка - висхідним вузлом. Спускається вузол, не показаний на малюнку, знаходиться на дальній стороні сфери. Символ - Перша точка Овна (нині в сузір'ї Риб), де екліптика перетинає екватор. Як видно з Сонця, Земля знаходиться на 22 вересня\(\Upsilon\) або близько. (На благо користувачів персональних комп'ютерів я знайшов символи, а\(\Upsilon\) в книжковій полиці Symbol 3.) \(\multimap\)

Нахил i - кут між площиною орбіти об'єкта і площиною екліптики (тобто орбіти Землі). Він лежить в діапазоні o 0 ≤ i < 180. Нахил більше 90o означає, що орбіта є ретроградною - тобто, що вона рухається навколо Сонця у напрямку, протилежному руху Землі.

Кут Ω, виміряний на схід від\(\Upsilon\) до\(mulitmapinv\), - це екліптична довгота висхідного вузла. (Слово «екліптика» зазвичай опускається як розуміється.) Вона йде від\(0^\circ\) до\(360^\circ\).