6.11: Рішення

6.11.1

Я думаю, що перше, що я б зробив, це перетворити координати в градуси і десяткові знаки (або, можливо, навіть радіани і десяткові, хоча я роблю це нижче в градусах і десяткових знаках):

Антарес:$α = 247.375 \quad δ = -26.433$
Денеб$α = 309.400 \quad δ = +45.283$

Ми вже зробили подібну проблему в розділі 3, розділ 3.5, приклад 2, тому я не буду робити це знову. Я роблю відповідь:

Один полюс:$α = 11^\text{h} 47^\text{m} .3 \quad δ = + 56^\circ 11^\prime$
Інший полюс:$α = 23^\text{h} 47^\text{m} .3 \quad δ = + 123^\circ 49^\prime$

6.11.2

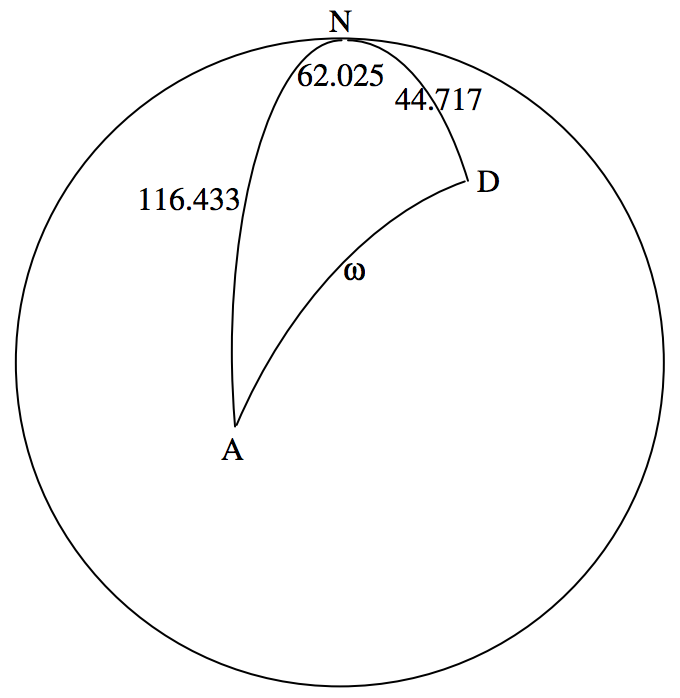
Я намалював Північний Небесний полюс$\text{N}$, а кольори від$\text{N}$ до Антарес ($\text{A}$) і до Денеба ($\text{D}$) разом з їх північно-полярними відстанями в градусах. Я також відзначив різницю між їх правими підйомами, у градусах. Ми можемо відразу обчислити, з правила косинуса для сферичних трикутників, Рівняння 3.5.2, кутова відстань$ω$ між двома зірками на небі. Я роблю це$ω = 91^\circ .190 \ 79$.

Тепер, коли ми знаємо кут між зірками, ми можемо використовувати плоский трикутник, щоб обчислити відстань між ними:

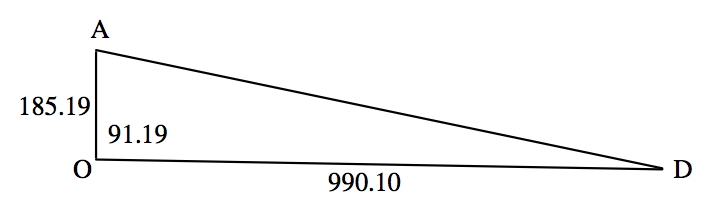
Я позначив Antares ($\text{A}$), Deneb ($\text{D}$$\text{O}$) і нас (), і відстані від нас до двох зірок, в парсеках. (Це взаємний їх паралаксів в arcsec.) Я також позначив кути, в градусах, між Антарес і Денеб. Тепер ми можемо використовувати правило косинуса для площин трикутників, Рівняння 3.2.2, щоб знайти відстань$\text{AD}$. Я роблю це 1011 парсеків.

Парсек - це відстань, на якій астрономічна одиниця (приблизно радіус орбіти Землі) буде підпорядковувати кут в одну дугову секунду. Це також означає, якщо ви подумаєте про це, що кількість астрономічних одиниць у парсеці дорівнює кількості кутових секунд в радіані, що є$360 \times 3600 \div (2π) = 2.062648 \times 10^5$. Отже, відстань між зірками є$1011 \times 2.062648 \times 10^5$ астрономічними одиницями. Помножте це на те$1.495 \ 98 \times 10^8$, щоб отримати відстань в км. Я роблю дистанцію$3.120 \times 10^{16} \ \text{km}$.

Це займе світлові$1.040596 \times 10^8$ секунди, щоб подорожувати, або 3298 років, тому відстань між зірками становить 3298 світлових років.

6.11.3

Давайте подивимося, чи зможемо ми розробити формулу для загального випадку. Ми будемо мати перший метеор почати$(α_{11}, \ δ_{11})$ і закінчити в$(α_{12}, \ δ_{12})$. Другий метеорит починається$(α_{21}, \ δ_{21})$ і закінчується в$(α_{22}, \ δ_{22}$. Нам належить знайти координати$(α, \ δ$ точки, від якої розходяться два метеори.

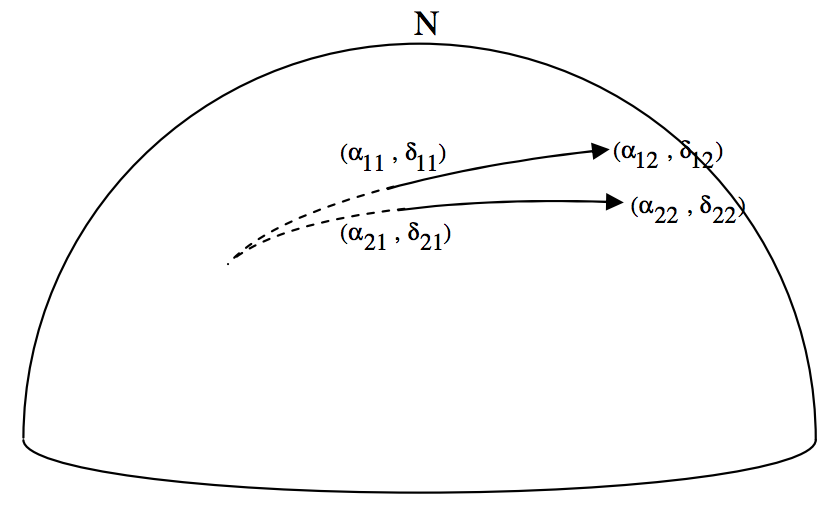
Це не особливо проста проблема - але є такою, яка, очевидно, корисна для метеоритних спостерігачів. Я просто викладу деякі пропозиції тут, і залишити читача, щоб опрацювати деталі. Я намалюю нижче один з метеорів, і променистий, і Північний Небесний полюс:

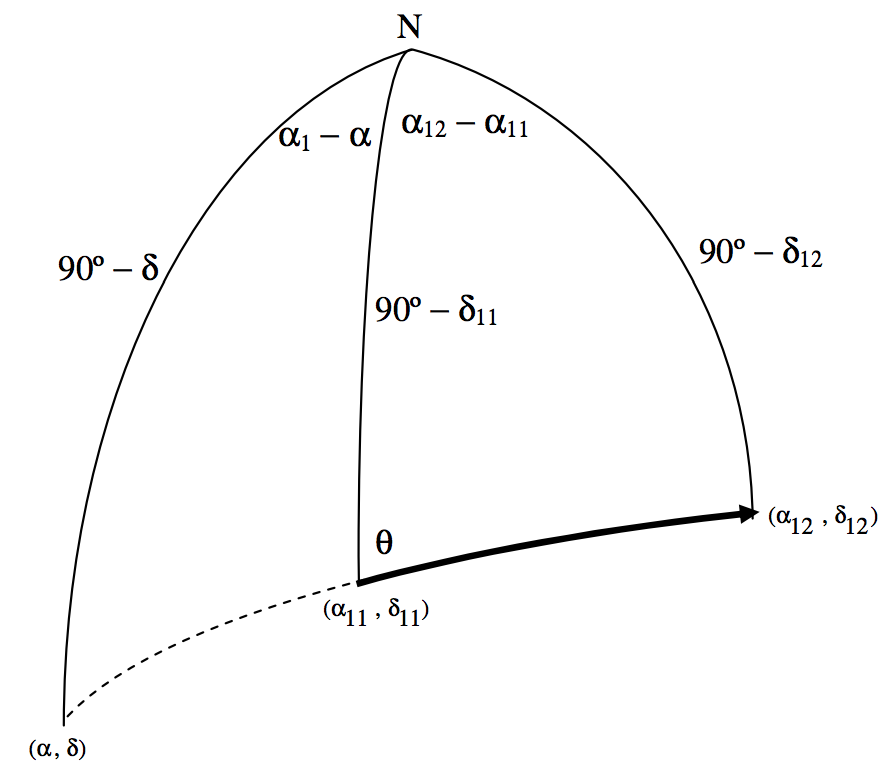
Скористайтеся правилом котангенса (Рівняння 3.5.5) на правосторонньому трикутнику, щоб отримати вираз для$\cot θ$:

$$\sin δ_{11} \cos (α_{12} - α_{11}) = \cos δ_{11} \tan δ_{12} + \sin (α_{12} - α_{11}) \cot θ.$$

Прирівняти ці два вирази для$\cot θ$ (тобто виключити$θ$ між двома рівняннями). Це дасть вам одне рівняння, що містить два невідомих$δ$,$α$ і все інше в Рівнянні є відомою величиною. (Це буде очевидно, якщо ви насправді робите числовий приклад.)

Тепер зробіть те ж саме для другого метеора, і ви отримаєте друге Рівняння в α і δ. В принципі, ви зараз вдома вільні, хоча може бути трохи важкої алгебри та тригонометрії, щоб пройти, перш ніж ви нарешті туди потрапите.

Відповідь я роблю наступним чином:

$$\tan α = \frac{\cos α_{22} \tan δ_{22} - \cos α_{12} \tan δ_{12} + a_1 \sin α_{12} - a_2 \sin α_{22}}{\sin α_{12} \tan δ_{12} - \sin α_{22} \tan δ_{22} + a_1 \cos α_{12} - a_2 \cos α_{22}},$$

де $$a_1 = \frac{\tan δ_{11}}{\sin(α_{11} - α_{12})} - \frac{\tan δ_{12}}{\tan(α_{11} - α_{12})}$$

і $$a_2 = \frac{\tan δ_{21}}{\sin(α_{21} - α_{22})} - \frac{\tan δ_{22}}{\tan(α_{21} - α_{22})}$$

Тоді $$\tan δ = \cos (α - α_{12}) \tan δ_{12} + \sin (α - α_{12} ) [\csc (α_{11} - α_{12}) \tan δ_{11} - \cot (α_{11} - α_{12}) \tan δ_{12}]$$

або $$\tan δ = \cos (α - α_{22}) \tan δ_{22} + \sin (α - α_{22} ) [\csc (α_{21} - α_{22}) \tan δ_{21} - \cot (α_{21} - α_{22}) \tan δ_{22}].$$

Будь-яке з цих двох рівнянь для$\tan δ$ має дати однаковий результат. У комп'ютерній програмі, яку я використовую для цього розрахунку, я отримую його для обчислення$\tan δ$ з обох рівнянь, як перевірка на помилки.

Це може здатися складним, але всі терміни є просто обчислюваними числами для будь-якого конкретного випадку. Якщо рівноцінний колір заважає (як це було - навмисно - у числовому прикладі, який я дав), я пропоную просто додати 24 години до всіх правильних підйомів.

Для числового прикладу, який я дав, я роблю координати променистого бути:

$$α = 22^\text{h} 01^\text{m}.3 \quad δ = - 00^\circ 37^\prime .$$

Дописувач

• Template:ContribTatum