6.5: Координати екліптики

У цифрах$\text{VI.2}$ і$\text{3}$ нас турбувало в основному щоденне обертання небесної сфери. На малюнку$\text{VI.4}$ ми будемо займатися головним чином річним рухом Сонця щодо зірок на небесній сфері. На відміну від цифр$\text{VI.2}$ і 3, я намалював небесний екватор, а не горизонт спостерігача, горизонтально, а північний небесний полюс, а не зеніт спостерігача, знаходиться у верхній частині діаграми. Встановлено, що для спостерігача на Землі Сонце рухається на схід щодо зірок протягом року, його правильне сходження безперервно зростає; цей видимий рух Сонця відносно зірок є, звичайно, наслідком обертання Землі навколо Сонця.

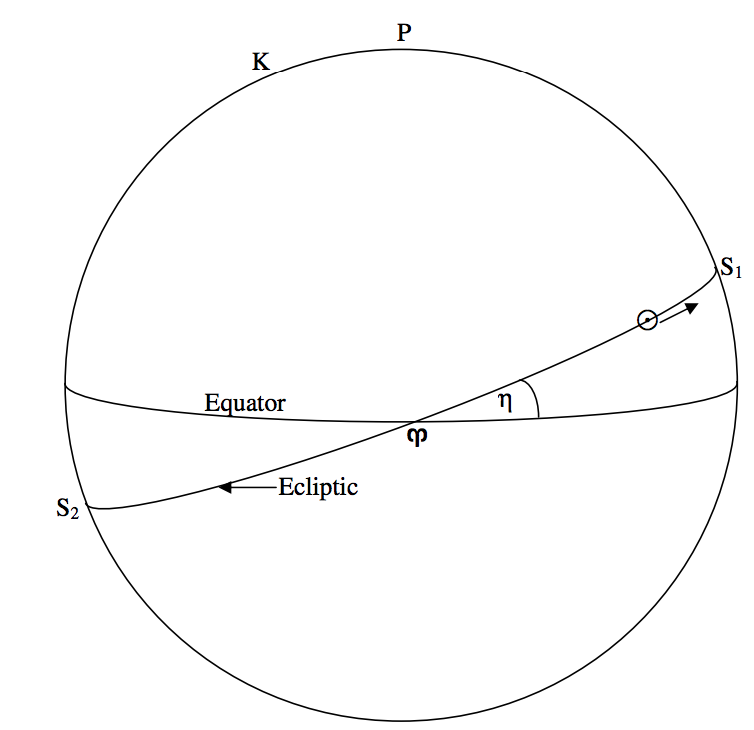
$\text{FIGURE VI.4}$

Щодо зірок встановлено, що протягом року Сонце рухається на схід по великому колу, який нахилений до екватора під кутом близько$23^\circ .4$. Це велике коло називається екліптикою, і вона є проекцією площини орбіти Землі на небесну сферу. Кут між екліптикою і екватором називається Наклонність екліптики. Екліптика перетинає екватор в двох точках. Сонце досягає однієї з цих точок приблизно 22 березня щороку на своєму шляху на північ, в цей час схилення Сонця змінюється від негативного до позитивного. Ця точка, висхідний вузол шляху Сонця на екваторі, є Першою Точкою Овна, яку ми ввели в Розділі 6.3. Як уже згадувалося там, і з причин, які будуть пояснені в розділі 6.7, насправді це в сузір'ї Риби, а не в Овні. Проте вона досі відома як Перша точка Овна і позначається астрологічним символом$\Upsilon$ для Овна. Це точка, з якої вимірюються праві підйоми. Момент часу, коли Сонце перетинає екватор з півночі на південь в Першій точці Овна, - це Березневе Рівнодення. Дні та ночі однакові по всьому світу на цю дату («рівнодення» = «рівна ніч»), і ця дата знаменує перший день Весни в північній півкулі. З цієї причини його також називають «весняним рівнодінням» (лат. verna = «весна») - але це навряд чи справедливо для астрономів південної півкулі, бо це знаменує початок південної осені.

Приблизно через три місяці, 21 червня або близько, Сонце досягає точки$S_1$ на червневому сонцестоянні (називається тими, хто живе в Північній півкулі, літнім сонцестоянням). Схилення Сонця тоді знаходиться в його найвищій точці,$+23.4$ градусах. У цей момент швидкість зміни відмінювання Сонця дорівнює нулю, що пояснює походження слова «сонцестояння», що означає, що Сонце на мить стоїть на місці. Сонце тоді знаходиться в сузір'ї Близнюків. Ще через три місяці Сонце спустилося назад до екватора на своєму шляху на південь, у вересневе рівнодення («осіннє рівнодення» для північян) 23 вересня або близько, коли Сонце знаходиться в сузір'ї Діви. І ще через три місяці Сонце досягає свого самого південного схилення в грудневе сонцестояння («зимове сонцестояння» для північян) 21 грудня або ближче до нього, коли Сонце знаходиться в сузір'ї Стрільця.

Також намальований на малюнку$\text{VI.4}$ Північний полюс екліптики$\text{K}$, який знаходиться в Драко. Південний полюс екліптики знаходиться в Дорадо.

Екліптика і її полюс K складають основу системи координат екліптики, проілюстрованої на малюнку$\text{VI.5}$. Довгота екліптики$λ$ та широта$β$ екліптики зірки$\text{X}$ показані на малюнку$\text{VI.5}$, який повинен бути зрозумілим. Для перетворення між екваторіальними та екліптичними координатами трикутник, який потрібно вирішити, - це трикутник$\text{PKX}$. Дуга$\text{KX}$ є$90^\circ − β$ і кут$\text{PKX}$ є$90^\circ − λ$. Що таке дуга$\text{PK}$, дуга$\text{PX}$ і кут$\text{KPX}$?

[Відповіді:$\text{PK} = η$ $\text{PX} = 90^\circ − δ$ $\text{KPX} = 90^\circ + α]$

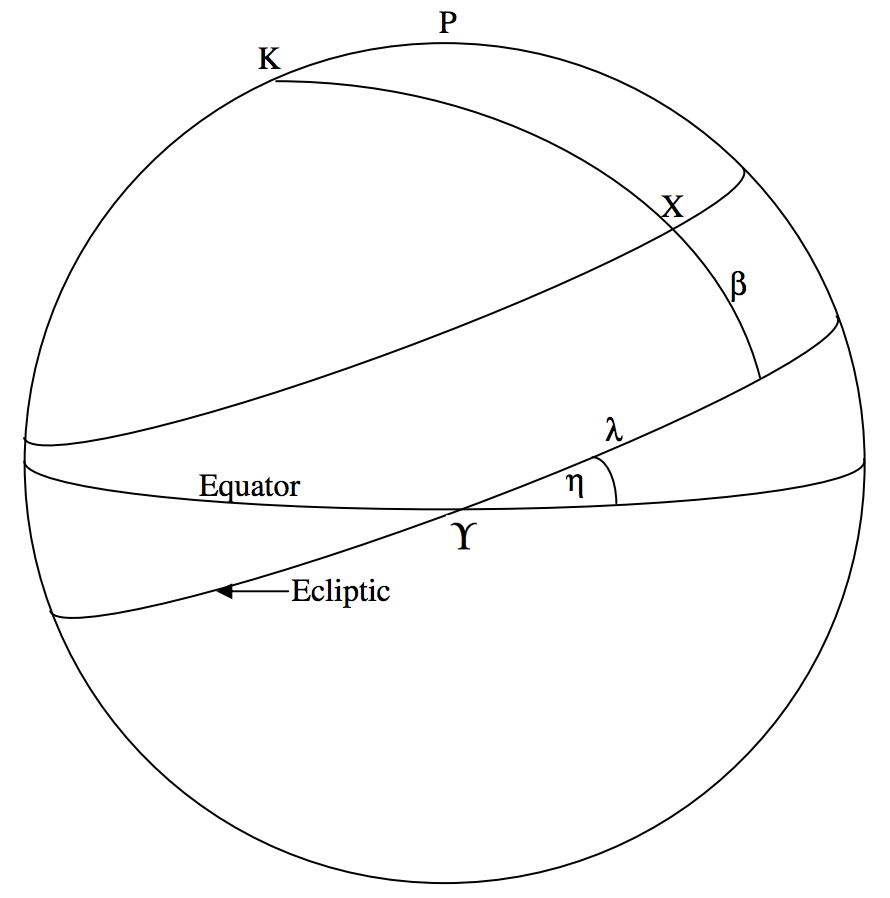
$\text{FIGURE VI.5}$