10.6: Обертальне розширення

Лінії в спектрі обертається зірки розширені, оскільки світло від відступаючої кінцівки червоне зміщене, а світло від наближається кінцівки синім. Можна зауважити, що зірки раннього типу (тип F і раніше), як правило, набагато швидші ротатори, ніж зірки пізнього типу, і, отже, зірки раннього типу демонструють більш обертальне розширення. Слід також зазначити, що полюсні ротатори, звичайно, не показують ротаційного розширення (навіть швидкі ротатори раннього типу).

Я буду дотримуватися астрономічного звичаю і посилатися на «червоне зсув» як зсув до більшої довжини хвилі, хоча для інфрачервоної лінії «червоне зсув» в цьому сенсі буде зміщенням від червоного! «Довгий» зрушення також не зовсім вирішує проблему з наступної причини. Хоча це правда, що відносність не робить різниці між рухомим джерелом і рухомим спостерігачем, у випадку ефекту Допплера в контексті звуку в повітрі, якщо спостерігач рухається, може бути зміна висоти сприйнятого звуку, але немає зміни довжини хвилі!

Почнемо з розгляду зірки, вісь обертання якої знаходиться в площині неба, і яка має рівномірне сяйво по всій її поверхні. Потім перейдемо до косих ротаторів, а потім до потемнілих зірок. Подальшим ускладненням, яке можна було б розглянути, було б нерівномірне обертання. Таким чином, Сонце не обертається як тверде тіло, але кутова швидкість на низьких широтах швидше, ніж на більш високих широтах — так зване «екваторіальне прискорення».

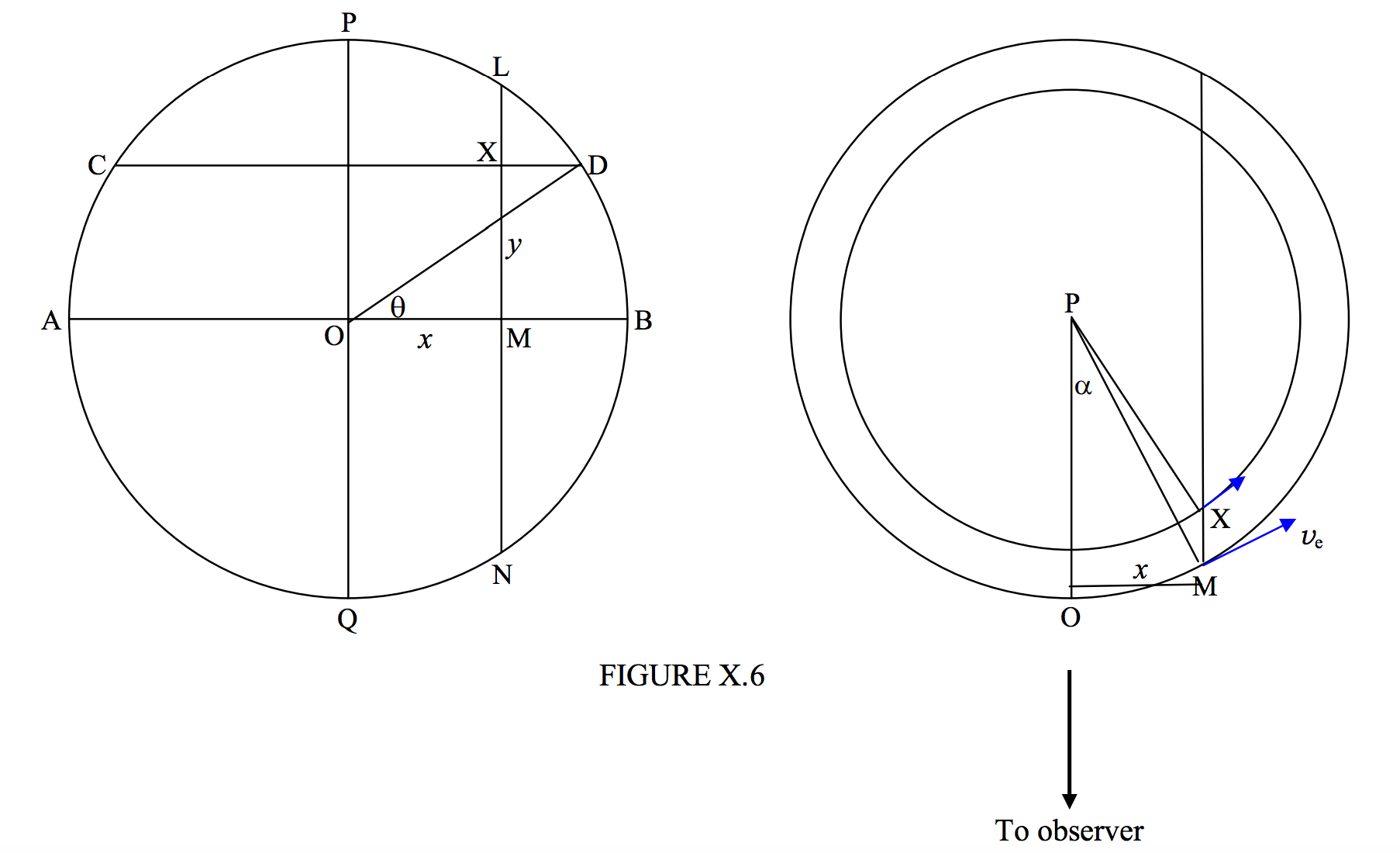
На малюнку X.6, на лівій руці ми бачимо диск зірки, як видно на небі спостерігачем. PQ - вісь обертання, яка повинна знаходитися в площині неба, а AB - екватор. X - точка на поверхні зірки в координатах\((x, y)\), широті\(\theta\). Зірка повинна обертатися з екваторіальною швидкістю\(v_e\). Те, що ми збираємося показати, це те, що всі точки на хорді LMN мають однакову радіальну швидкість від або до спостерігача, і, отже, все світло від точок на цій хорді має однаковий доплерівський зсув.

У правій частині малюнка зображена зірка, видна зверху полюса П. Мале коло - це паралель широти CD, показана на лівій частині малюнка.

M - точка на екваторі, а також на акорді LMN. Його швидкість є\(v_e\) і радіальна складова його швидкості є\(v_e \sin \alpha\). Швидкість точки М дорівнює\(v_e \cos \theta\), а її радіальна швидкість дорівнює\(v_e \cos \theta \sin \text{OPX}\). Але\(x = \text{PM} \sin \alpha = a \sin \alpha\text{ and }x = \text{PX} \sin \text{OPX} = a \cos \theta \sin \text{OPX}\). Тому\(\cos \theta \sin \text{OPX} = \sin \alpha\). Тому радіальна швидкість X дорівнює\(v_e \sin \alpha\), яка така ж, як і у М, і тому всі точки на хорді LMN мають радіальну швидкість\(v_e \sin \alpha = v_e x/a\).

Тому всі точки на\(x =\) константі хорди піддаються одному і тому ж доплерівському зсуву.

\[\label{10.7.1}\dfrac{\Delta \lambda}{\lambda}=\dfrac{v_e x}{ac}.\]

Ордината профілю лінії випромінювання при доплерівському зсуві\(\Delta \lambda\) порівняно з її ординатою в центрі лінії дорівнює відношенню довжини\(x =\) константи хорди до діаметра\(2a\) зоряного диска:

\[\label{10.7.2}\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=\left ( 1-\frac{x^2}{a^2}\right )^{\frac{1}{2}}=\left ( 1-\frac{c^2\left (\Delta \lambda \right )^2 }{v_e^2\lambda^2}\right )^\frac{1}{2}.\]

У вищесказаному ми припустили, що вісь обертання знаходиться в площині неба, або що нахил\(i\) екватора до площини неба є\(90^\circ\). Якщо нахилу немає\(90^\circ\), єдиний ефект полягає в тому, що всі радіальні швидкості зменшуються в коефіцієнт\(\sin i\), так що Equation\ ref {10.7.2} стає

\[\label{10.7.3}\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=\left ( 1-\frac{c^2\left ( \Delta \lambda \right )^2}{v_e^2 \sin^2 i \lambda^2}\right )^\frac{1}{2},\]

і це профіль лінії. Це еліпс, і якщо ми запишемо\(\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=X \text{ and }\frac{\Delta \lambda}{\lambda}=Y\) Equation\ ref {10.7.3} можна записати

\[\label{10.7.4}\frac{x^2}{\left ( \frac{v_e \sin i}{c}\right )^2}+\frac{y^2}{1^2}=1.\]

Базальна ширина лінії (яка не має асимптотичних крил) є\(\frac{2v_e \sin i}{c}\) і FWHM є\(\frac{\sqrt{3}v_e\sin i}{c}\). Профіль лінії поглинання центральної\(d\) глибини

\[\label{10.7.5}\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=1-d\left (1-\frac{c^2 \left (\Delta \lambda \right )^2}{v_e^2\sin^2 i\lambda^2}\right )^\frac{1}{2},\]

Залишається як вправа, щоб показати, що

\[\text{Equivalent width}=\frac{\pi}{\sqrt{12}}\times \text{central depth}\times \text{FWHm}=0.9069 dw .\label{10.7.6}\]

З ширини ротаційно розширеної лінії ми можемо визначити\(v_e \sin i\), але ми не можемо визначити\(v_e\text{ and }i\) окремо без додаткової інформації. Так само ми не можемо визначити кутову швидкість обертання, якщо не знаємо радіус незалежно.

Можна відзначити, що для обертової планети, видимої лише відбитим світлом, ефект Допплера подвоюється відображенням, тому базальна ширина ротаційно розширеної лінії дорівнює

\[\dfrac{4v_e \sin i}{c}. \nonumber\]

Тепер розберемо ефект потемніння кінцівок. Я збираюся використовувати інтенсивність і сяйво слів у їх строго правильних сенсах, як описано в главі 1, і символи\(I\text{ and }L\) відповідно. Тобто сяйво = інтенсивність на одиницю проектованої площі. Для спектральної інтенсивності та спектрального сяйва - тобто інтенсивності та сяйва на одиницю інтервалу довжини хвилі, я використовую індекс\(\lambda\).

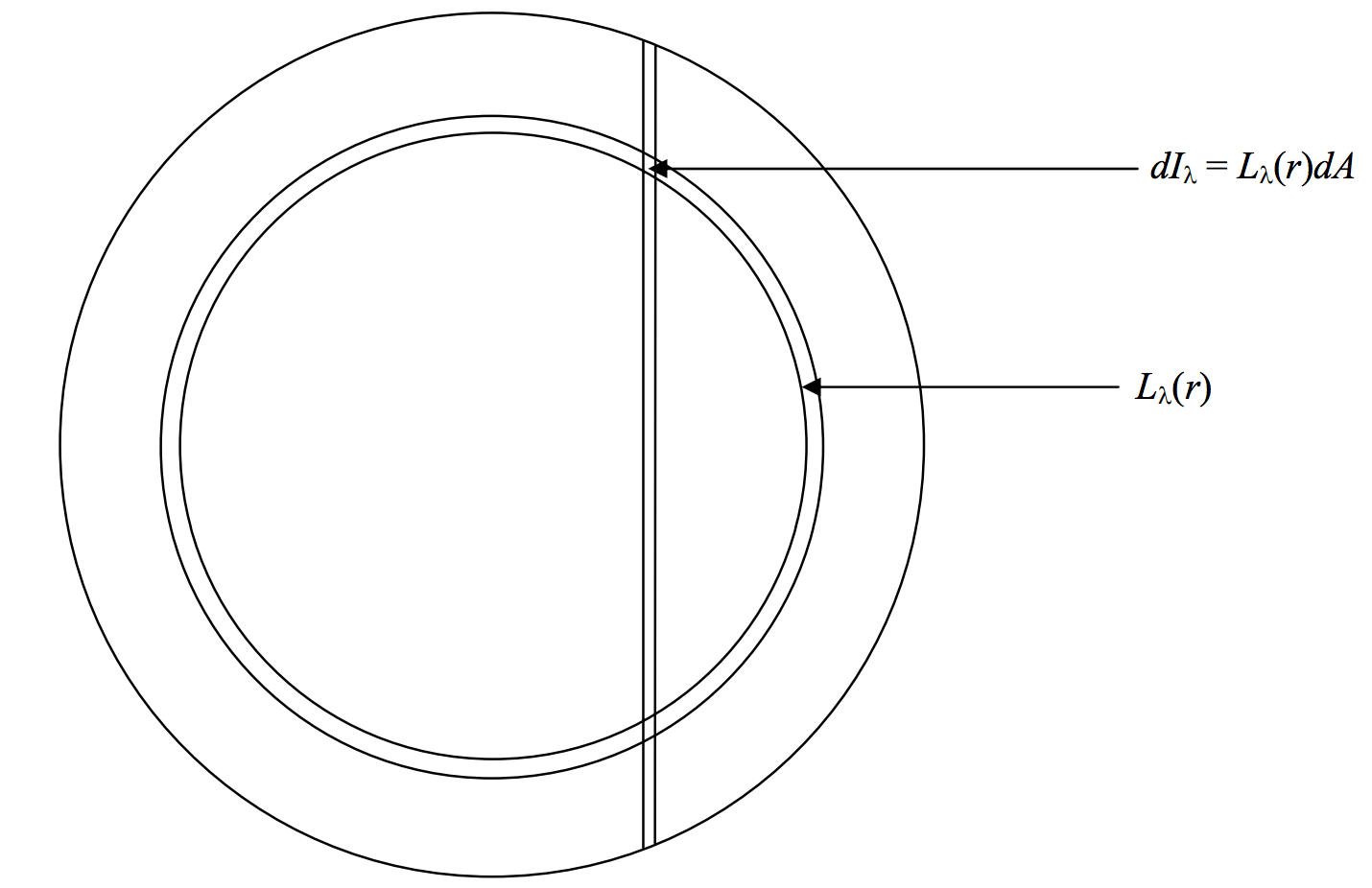
\(\text{FIGURE X.7}\)

Припускаємо, що спектральне сяйво на відстані\(r\) від центру диска є\(L_\lambda (r)\). Інтенсивність від елементарної області\(dA\) на диску є\(dI_\lambda = L_\lambda (r)dA\). Площа між вертикальною смугою і кільцевим кільцем на малюнку Х.7 трохи паралелограма довжини\(dy\) і ширини\(dx\), так що\(dA = dxdy\). Ось\(y^2 = r^2 - x^2\), щоб

\[dy=\frac{rdr}{y}=\dfrac{rdr}{\sqrt{r^2-x^2}}. \nonumber\]

Тому\(dA=\frac{rdrdx}{\sqrt{r^2-x^2}}\). Сумарна інтенсивність від смуги ширини\(dx\), яка є\(dI_\lambda (\Delta \lambda)\), де\(\frac{\Delta \lambda}{\lambda}=\frac{xv_e \sin i}{ac}\), дорівнює

\[\label{10.7.7}dI_\lambda (\Delta \lambda) = 2\int_x^a \dfrac{L_\lambda (r)rdr}{\sqrt{r^2-x^2}}dx.\]

Профіль лінії (емісії)

\[\label{10.7.8}\frac{I_\lambda (\Delta \lambda)}{I_\lambda (0)}=\dfrac{\int_x^a \frac{L_\lambda (r)rdr}{\sqrt{r^2-x^2}}dx}{\int_0^a L_\lambda (r)dr},\]

який є лінійним профілем. Як вправу, подивіться, чи можете ви знайти вираз для профілю лінії, якщо limb=затемнення задано\(L_\theta =L(0)[1-u(1-\cos \theta)]\), і показати, що якщо коефіцієнт затемнення кінцівок\(u = 1\), профіль параболічний.

Рівняння\ ref {10.7.8} дозволяє обчислити профіль лінії, враховуючи потемніння кінцівки. Більш практичною, але складнішою проблемою є інвертування Рівняння і, виходячи з спостережуваного профілю лінії, знайти потемніння кінцівки. Приклади цього інтеграла та його інверсії розв'язком інтегрального рівняння наведено Татумом та Яворським, Й.Квантом. Спектр. Рад. Трансфер, 38, 319, (1987).

Подальшим пошуком цієї проблеми було б обчислити профіль лінії рівномірної зірки, яка обертається швидше на екваторі, ніж на полюсах, а потім для зірки, яка одночасно затемнена і екваторіально прискорена, - а потім подивитися, чи можна однозначно перевернути задачу і визначити обидві кінцівки. затемнення і екваторіальне прискорення від лінійного профілю. Це було б досить складним завданням.