10.5: Розширення тиску

Last updated
Save as PDF

Page ID: 77791

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Це досить складний предмет, і я не експерт в ньому. Читач пробачить мене, якщо я відповідним чином відношуся до нього досить коротко і описово.

Явища розширення тиску (також відомі як розширення зіткнення) часто поділяються на ефекти, що виникають внаслідок короткого часового інтервалу між атомними зіткненнями, та ефекти, що виникають у момент зіткнення. Почну з опису першого з цих явищ.

Єдиною можливою абсолютно монохроматичною нерозширеною нескінченно вузькою лінією з єдиною, однозначно визначеною частотою є синусоїда нескінченної протяжності. Синусоїда скінченної довжини не є істинною синусоїдою однієї частоти, але вона має розкид складових частот, який можна визначити за допомогою аналізу Фур'є. Це, до речі, є причиною принципу невизначеності Гейзенберга (Unsicherheitsprinzip). Якщо хвильова функція, яка описує частку, дуже обмежена за ступенем, то положення частинки відносно добре визначається. З іншого боку, обмежена ступінь хвильової функції означає, що вона має відповідно широкий розкид Фур'є складових довжин хвиль, і, отже, імпульс відповідно невизначений.

Атмосфери гігантських і надгігантських зірок відносно тонкі; розширення тиску невелике, а лінії, як правило, вузькі. Однак в атмосферах зірок головної послідовності часті зіткнення між атомами. Часте виникнення зіткнень перериває хвильові поїзди і ділить їх на короткі хвильові пакети, з відповідним розкидом складових частот. Таким чином, лінії спектра розширюються.

Розподіл Фур'є амплітуд складових частот синусоїди, яка усічена коробчастою функцією, таке ж, як і розподіл Фур'є амплітуд світлової хвилі, дифрагованої єдиною щілиною. Тобто це sinc функція форми,\((\sin \Delta ν)/ \Delta ν\) і розподіл інтенсивності є квадратом цього. Чим коротший час міжзіткнення, тим ширше поширення складових частот, так само, як вузька щілина виробляє широку дифракційну картину. Таким чином, можна очікувати, що профіль розширеної лінії тиску буде нагадувати одну щілинну дифракційну картину, яка, як буде нагадано, виглядає як малюнок X.5.

альт
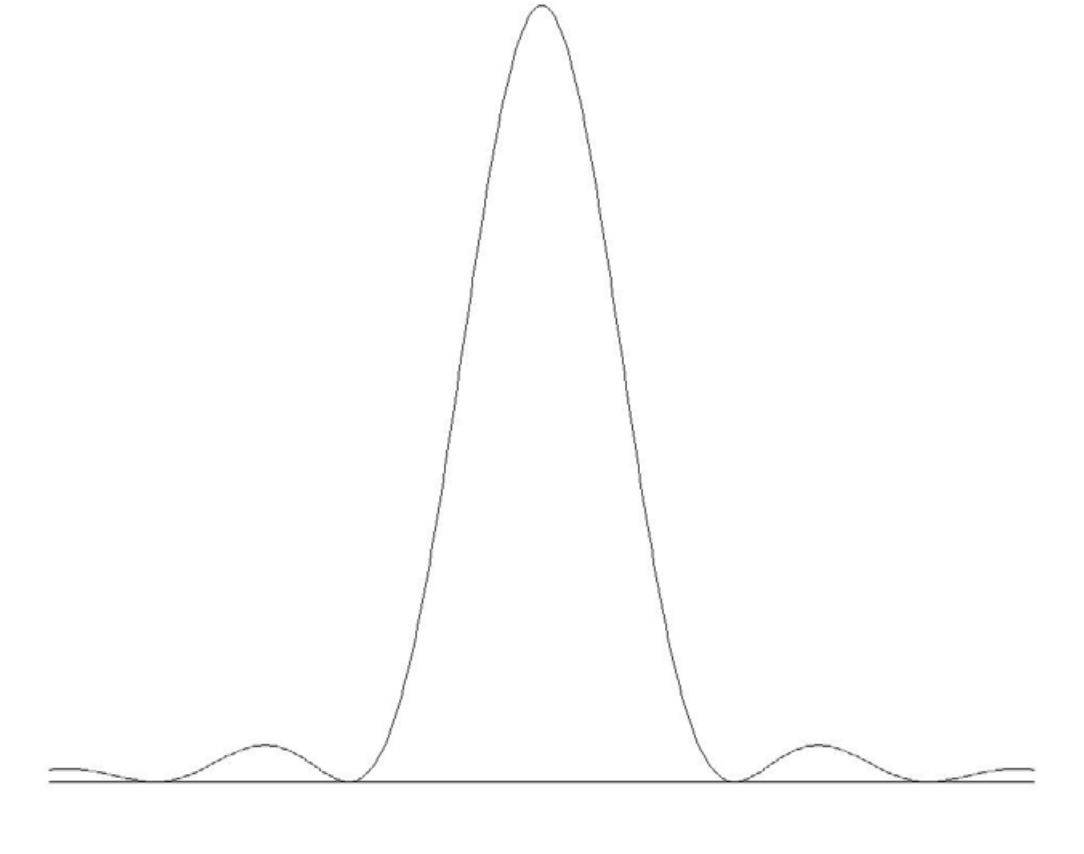
\(\text{FIGURE X.5}\)

Профіль дійсно виглядав би так, якби всі часи міжзіткнення були точно рівні, а всі фрагменти хвильового поїзда були точно однакової довжини. Існує, однак, розподіл Пуассона міжколізійних часів, і тому вищевказаний профіль повинен бути узгоджений з цим розподілом Пуассона. Хоча я не роблю обчислення тут, отриманий профіль є профілем Лоренца, за винятком того, що демпфуюча константа\(\Gamma\) замінюється на\(2 / \overline t\), де\(\overline t\) середній час між зіткненнями. Середній час між зіткненнями дається, з кінетичної теорії газів,

\[\label{10.6.1}\overline t =\frac{1}{nd^2}\sqrt{\frac{m}{16\pi kT}}.\]

\(m,\, d\text{ and }n\)Ось, відповідно, маси, діаметри і щільність чисел атомів. Отже, якщо кінетична температура відома незалежно, щільність чисел частинок може бути визначена з FWHm розширеної під тиском лінії.

Нагадаємо, що класична теорія гасіння випромінювання пророкує однаковий FWHm для всіх ліній, з класичною постійною демпфування\(\gamma\). Квантова механічна теорія передбачає демпфуючу\(\Gamma\) константу і, отже, FWHm, яка відрізняється від лінії до лінії. Проте в спектрі зірки головної послідовності досить часто виявляється, що всі лінії даного елемента мають однаковий FWHm і, отже, однакову ефективну демпфуючу константу. Це пояснюється тим, що ширина профілю Лоренца визначається більше розширенням тиску, ніж демпфуванням випромінювання.

Існують подальші ефекти розширення, викликані взаємодіями, які відбуваються в момент зіткнення. Якщо атом наближається електрон або іон, він тимчасово буде знаходитися в електричному полі, і, отже, лінії будуть розширені ефектом Старка, який може бути або лінійним (пропорційним електричному полю\(E\)), або квадратичним (\(\propto E^2\)), або нейтрально-нейтральним реакціям породжують взаємодії між тимчасово індукованими дипольними моментами (сили ван дер Ваальса), і всі вони мають різні залежності від міжатомної відстані. Нейтральний магній дуже чутливий до квадратичного ефекту Старка, а водень чутливий до лінійного ефекту Старка. Вся тема досить складна, і я залишаю його тут, крім того, щоб вказати на дві дрібні деталі. Дуже часто розширення не є симетричним, лінії, як правило, мають ширші крила до довгохвильової сторони, ніж на стороні короткої довжини хвилі. Це пов'язано з тим, що ефект взаємодії полягає в зниженні та розширенні енергетичних рівнів переходу, нижній рівень енергії, як правило, знижується більше, ніж верхній. Другий момент полягає в тому, що водневі лінії Балмера часто значно розширені лінійним ефектом Старка, і це можна розпізнати, оскільки шаблон Старка для серії Бальмера такий, що немає незміщених компонентів Старка для навіть членів серії -\(\text{H}\beta,\, \text{H}\delta,\, \text{H}ζ,\) тощо Таким чином призводить до центрального падіння до ці лінії в спектрі випромінювання або центральний удар в лінії поглинання.