10.4: Комбінація профілів

У рядку може бути одночасно кілька факторів розширення. Два механізми можуть мати подібні профілі (наприклад, теплове розширення та мікротурбулентність) або вони можуть мати зовсім різні профілі (наприклад, теплове розширення та гасіння випромінювання). Нам потрібно знати отриманий профіль, коли присутній більше одного розширювального агента. Розглянемо емісійну лінію, і давайте\(x = \lambda - \lambda_0\). Припустимо, що лінії розширені, наприклад, шляхом теплового розширення, тобто функція теплового розширення\(f(x)\). Припустимо, однак, що, крім того, лінії також розширені за рахунок гасіння випромінювання, профіль демпфування випромінювання\(g(x)\). На відстані\(ξ\) від центру лінії внесок у профіль лінії - це висота функції,\(f(ξ)\) зваженої функцією\(g(x - ξ)\). Тобто отриманий профіль\(h(x)\) задається

\[\label{10.5.1}h(x)=\int_{-\infty}^\infty f(ξ)g(x-ξ)\,dξ.\]

Читач повинен переконати його- або себе, що це точно так само, як

\[\label{10.5.2}h(x)=\int_{-\infty}^\infty f(x-ξ)g(ξ)\,dξ.\]

Цей профіль називається згорткою двох складових профілів, і часто пишеться символічно.

\[\label{10.5.3}h=f\ast g .\]

Складання двох гаусових функцій

Розглянемо, наприклад, згортку двох гауссових функцій, наприклад згортку теплового і мікротурбулентного розширення.

Припустимо, однією з функцій Гаусса є

\[\label{10.5.4}G_1(x)=\frac{1}{g_1}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left (-\frac{x^2\ln 2}{g_1^2}\right )=\frac{0.46972}{g_1}\text{exp}\left (-\frac{0.69315x^2}{g_1^2}\right ).\]

Ось\(x=\lambda -\lambda_0\). Площа під кривою - єдність, HWHM -\(g_1\) і пік\(\frac{1}{g_1}\sqrt{\frac{\ln 2}{\pi}}\). (Переконайтеся в цьому.) Припустимо, що друга функція Гаусса

\[\label{10.5.5}G_2(x)=\frac{1}{g_2}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left ( -\frac{x^2\ln 2}{g_2^2}\right).\]

Тепер можна показати, використовуючи Equation\ ref {10.5.1} або\ ref {10.5.2}, що згортка\(G_1\text{ and }G_2\) є

\[\label{10.5.6}G(x)=G_1(x)\ast G_2(x)=\frac{1}{g}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left (-\frac{x^2\ln 2}{g^2}\right ),\]

де

\[\label{10.5.7}g^2=g_1^2+g_2^2.\]

Цей результат ми використовували вже в Розділі 10.4, коли, додаючи мікротурбулентність до теплового розширення, ми підставили\(\sqrt{V_\text{m}^2+ξ_\text{m}^2}\) на\(V_\text{m}\). Якщо ви вважаєте, що інтеграція є клопіткою, я зробив це в Додатку до цієї глави.

Складання двох лоренціанських функцій

Тепер розглянемо поєднання двох лоренціанських функцій. Випромінювання випромінювання породжує лоренціанський профіль, і пізніше ми побачимо, що розширення тиску також може призвести до лоренціанського профілю. Припустимо, що два лоренціанські профілі

\[\label{10.5.8}L_1(x)=\frac{l_1}{\pi}\cdot\frac{1}{x^2+l_1^2}\]

і

\[\label{10.5.9}L_2(x)=\frac{l_2}{\pi}\cdot \frac{1}{x^2+l_2^2}.\]

Ось\(x=\lambda -\lambda_0\). Площа під кривою - єдність, HWHM -\(l_1\) і пік\(1/(\pi l)\). (Переконайтеся в цьому.) Можна показати, що

\[\label{10.5.10}L(x)=L(x)\ast L_2(x)=\frac{1}{\pi}\cdot \frac{1}{x^2+l^2},\]

де

\[\label{10.5.11}l=l_1+l_2.\]

Деталі інтеграції наведені в Додатку до цієї глави.

Свернення функції Лоренца з функцією Гаусса

Давайте тепер подивимося на згортку гауссового профілю з лоренцівським профілем; тобто згортку

\[\label{10.5.12}G(x)=\frac{1}{g}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left ( -\frac{x^2\ln 2}{g}\right ) \]

із

\[\label{10.5.13}L(x)=\frac{1}{\pi}\cdot \frac{1}{x^2+l^2}.\]

Ми можемо знайти згортку з рівняння\ ref {10.5.1} або з Equation\ ref {10.5.2}, і отримаємо або

\[\label{10.5.14}V(x)=\frac{1}{g}\sqrt{\frac{\ln 2}{\pi^3}}\int_{-\infty}^\infty \frac{\text{exp}\left ( -[(ξ-x)^2\ln 2]/g^2\right ) }{ξ^2+l^2}dξ\]

або

\[\label{10.5.15}V(x)=\frac{1}{g}\sqrt{\frac{\ln 2}{\pi^3}}\int_{-\infty}^\infty \frac{\text{exp}[-(ξ^2\ln 2)/g^2]}{(ξ-x)^2+l^2}\,dξ.\]

Вираз\ ref {10.5.14} або\ ref {10.5.15}, що є згорткою гаусового та лоренціанського профілю, називається профілем Фойгта. (Груба спроба вимови була б чимось на зразок Фохта.)

Корисним параметром для опису «gaussness» або «lorentzness» профілю Voigt може бути

\[\label{10.5.16}k_G=\frac{g}{g+l},\]

що дорівнює 0 для чистого профілю Лоренца і 1 для чистого профілю Гаусса. На малюнку X.4 я намалював профілі Фойгта для\(k_G = 0.25, 0.5\text{ and }0.75\) (суцільний, пунктирний і пунктирний відповідно). Профілі нормуються так, щоб всі мали однакову площу. Приємною вправою для тих, хто більш терплячий і компетентний з комп'ютерами, ніж я, було б намалювати 1001 профілі Voigt, з\(k_G\) переходом від 0 до 1 з кроком 0,001, можливо, нормалізується все на тій же висоті, а не на тій же площі, і зробити фільм Гаусового профілю поступово перетворюючись на лоренціанський профіль. Дайте мені знати, якщо вам це вдасться!

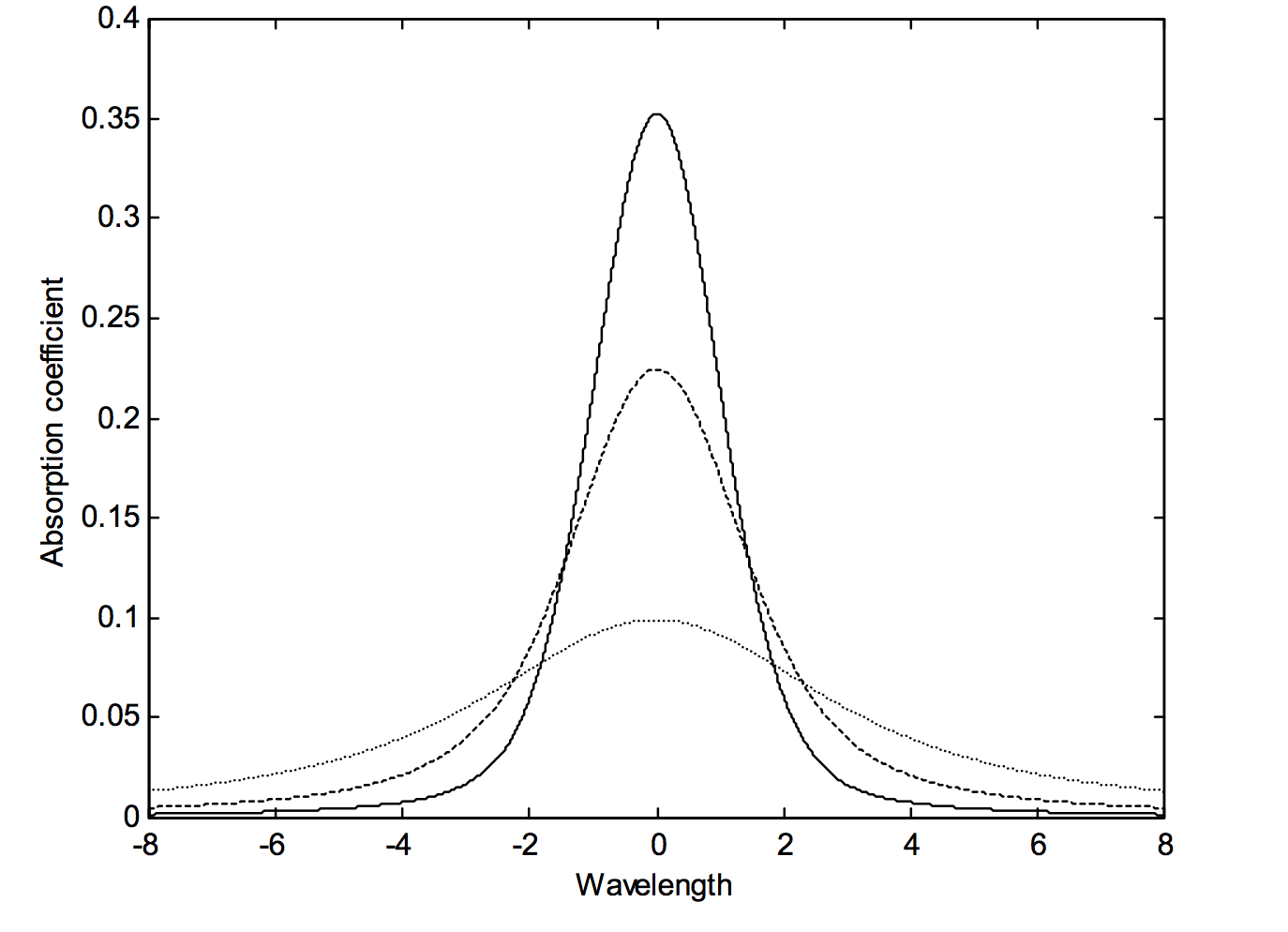
\(\text{FIGURE X.4}\)

Що стосується профілів gauss-gauss та lorentz-lorentz, я додав деякі деталі інтеграції профілю gauss-lorentz у Додатку до цієї глави.

FWHM або FWHm в одиницях довжини хвилі гаусового профілю (тобто\(2g\)) є

\[\label{10.5.17}w_G = \frac{\left ( 2kT/m +ξ_\text{m}^2\right )^{\frac{1}{2}}\lambda_0\sqrt{ln 16}}{c}=\frac{1.665 \left ( 2kT/m +ξ_\text{m}^2 \right )^{\frac{1}{2}}\lambda_0}{c}.\]

FWHM або FWHm в одиницях частоти лоренціанського профілю є

\[\label{10.5.18}w_L = \Gamma /(2\pi)=0.1592 \Gamma ,\]

\(\Gamma\)Ось сума постійної гасіння випромінювання (див. Розділ 2) і внесок від розширення тиску\(2 /\overline t\) (див. Розділ 6). Для FWHM або FWHm в одиницях довжини хвилі (тобто\(2l\)), ми повинні помножити на\(\lambda_0^2 /c\).

Інтеграція профілю Voigt

Площа під профілем Фойгта - це\(2\int_0^\infty V(x)\,dx\), де\(V(x)\) задається Equation\ ref {10.5.14}, яке саме потрібно було оцінювати за допомогою числового інтегрування. Оскільки профіль симетричний\(x = 0\), ми можемо інтегрувати з\(0\text{ to }\infty\) і помножити на 2. Незважаючи на це, подвійний інтеграл може здатися грізним завданням. Особливо клопітно було б інтегрувати майже лоренціанський профіль з великими крилами, тому що тоді виникла б проблема того, як далеко піти на верхню межу. Однак це зовсім не грізне завдання. Площа під кривою, заданою рівнянням\ ref {10.5.14}, є одиницею! Це легко побачити з фізичного прикладу. Профіль, заданий Equation\ ref {10.5.14}, є згорткою лоренціанського профілю Рівняння\ ref {10.5.13} з гауссовим профілем рівняння\ ref {10.5.12}, обидва з яких були нормовані на одиницю площі. Уявімо, що емісійна лінія розширюється за рахунок гасіння випромінювання, так що її профіль є лоренціанським. Тепер припустимо, що він додатково розширюється термічним розширенням (Гаусовим профілем), щоб закінчити як профіль Фогта. (Крім того, припустимо, що лінія сканується спектрофотометром з функцією гаусової чутливості.) Зрозуміло, що до тих пір, поки лінія завжди оптично тонка, додаткове розширення не впливає на інтегровану інтенсивність.

Тепер ми згадували в розділах 2 та 3 цієї глави, що еквівалентну ширину лінії поглинання можна обчислити з\(c \times\text{ central depth }\times\) FWHm, а також площа емісійної лінії -\(c \times\text{ height }\times\) FWHM, де\(c\text{ is }1.064 ( = \sqrt{\pi / \ln 16} )\) для гаусового профілю та\(1.571 (= \pi/2)\) для лоренціанського профілю. Ми знаємо, що інтеграл\(V(x)\) - це єдність, і це досить проста справа, щоб обчислити як висоту, так і FWHM\(V(x)\). З цього стає можливим обчислити константу\(c\) як функцію гауссового дробу\(k_G\). Результат виконання цього показаний на малюнку Х.4А.

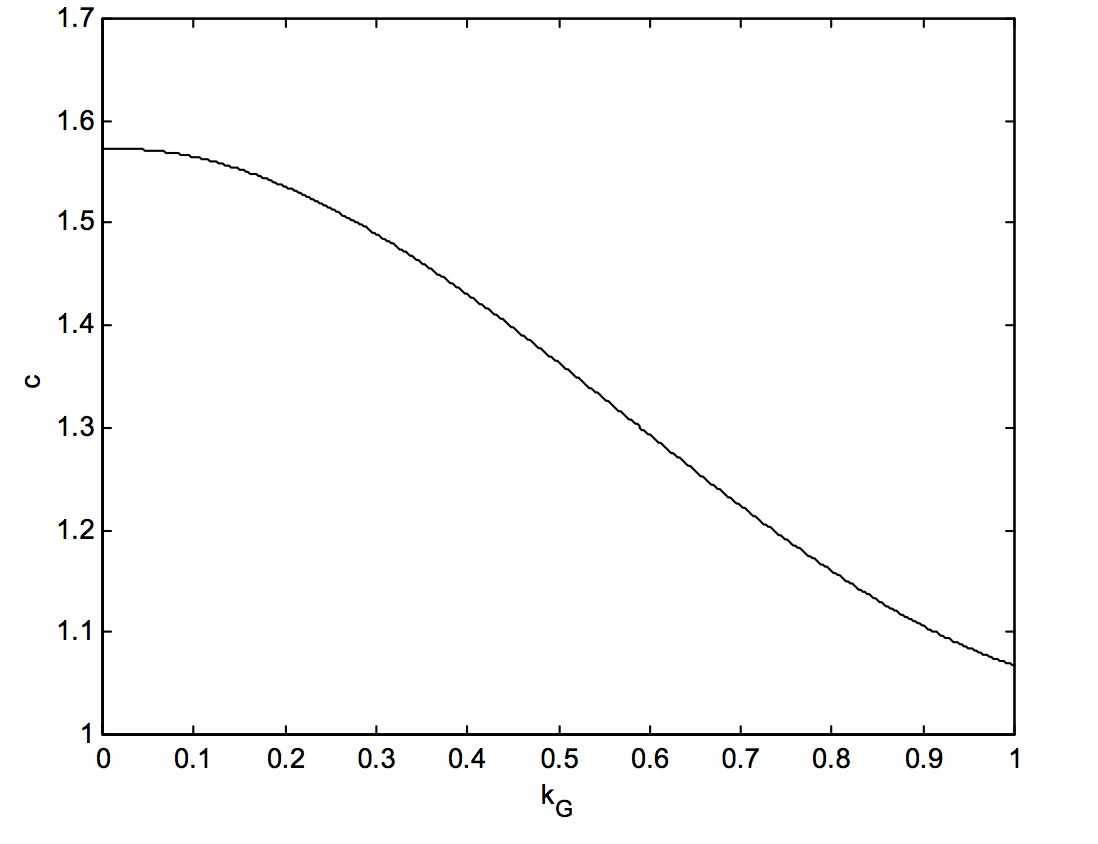
\(\text{FIGURE X.4A}\)

Ця крива може бути оснащена емпіричним рівнянням

\[\label{10.5.19}c=a_0+a_1k_G+a_2k_G^2+a_3k_G^3,\]

де\(a_0 = 1.572,\, a_1 = 0.05288,\, a_2 = -1.323\text{ and }a_3 = 0.7658\). Похибка, що виникла при використанні цієї формули, ніде не перевищує 0,5%; середня похибка - 0,25%.

Профіль Voigt з точки зору оптичної товщини в центрі лінії.

Ще один спосіб написати профіль Voigt, який може бути корисним:

\[\label{10.5.20}\tau (x) = Cl \tau (0) \int_{-\infty}^\infty \frac{\text{exp}[-(ξ-x)^2\ln 2/g^2]}{ξ^2+l^2}\,dξ .\]

Тут\(x = \lambda - \lambda_0\) і\(ξ\) знаходиться фіктивна змінна, яка зникає при виконанні певного інтеграла. Гаусова HWHM є\(g=\lambda_0 V_\text{m} \sqrt{\ln 2}/c\), а лоренціанський HWHM є\(l=\lambda_0^2 \Gamma /(4\pi c)\). Оптична товщина в\(\lambda - \lambda_0 = x\) є\(\tau (x)\), а оптична товщина в центрі лінії\(\tau (0)\). \(C\)є безрозмірним коефіцієнтом, значення якого залежить від гауссового дробу\(k_G =g/(g+l)\). \(C\)чітко дається

\[\label{10.5.21}Cl \int_{-\infty}^\infty \frac{\text{exp}[-ξ^2\ln 2/g^2]}{ξ^2+l^2}\,dξ =1.\]

Якщо ми тепер дозволимо\(l = l^\prime g / \sqrt{\ln 2}\) і\(ξ = ξ^\prime g / \sqrt{\ln 2}\), а також використовувати симетрію integrand про\(ξ = ξ^\prime = 0\), це стає

\[\label{10.5.22}2Cl^\prime \int_0^\infty \frac{\text{exp}\left ( -ξ^{\prime 2}\right ) }{ξ^{\prime 2}+l^{\prime 2}}dξ^\prime =1.\]

На підстановці\(ξ^\prime =\frac{2l^\prime t}{1-t^2}\) (щоб зробити межі кінцевими) отримуємо

\[\label{10.5.23}4C \int_0^1 \frac{\text{exp}[-\{2l^\prime t/(1-t^2)\}^2 ]}{1+t^2}\,dt =1,\]

які можуть бути легко чисельно інтегровані для заданого значення\(l^\prime\). Нагадаємо, що\(l/g=1/k_G -1\) і значить, що\(l^\prime = (1/k_G -1)\sqrt{\ln 2}\). Результати інтеграції такі. Колонка\(C_{\text{approx}}\) пояснюється наступним малюнком X.4B.

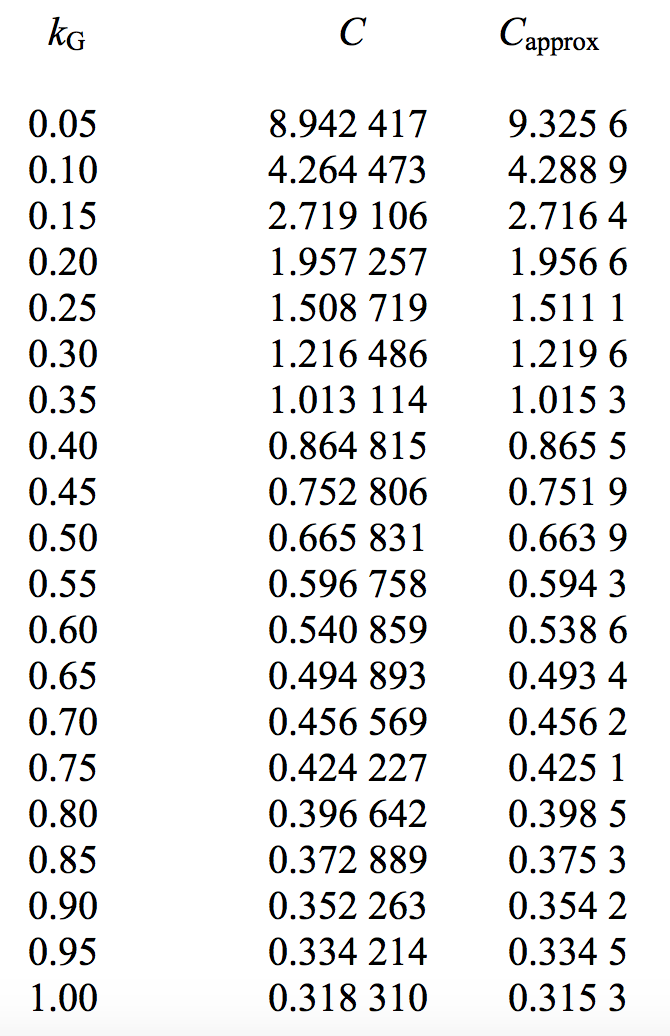
Останній запис, значення\(C\) for\(k_G = 1\), чистий профіль Гаусса, є\(1/\pi\). Ці дані зображені на малюнку X.4B.

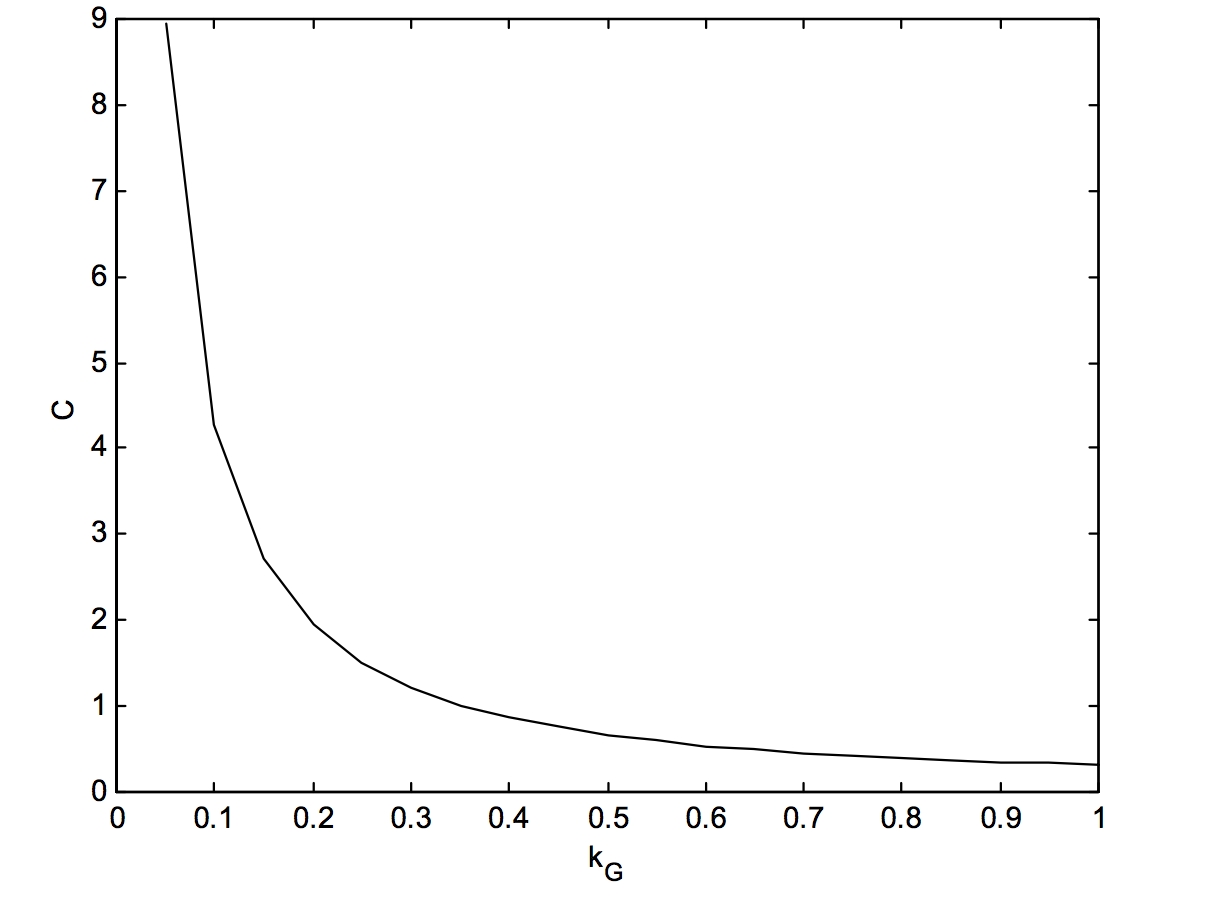
\(\text{FIGURE X.4B}\)

емпірична формула

\[\label{10.5.24}C_\text{approx}=ak_G^{-b}+c_0+c_1k_G+c_2k_G^2+c_3k_G^3,\]

де

\[\nonumber\begin{align} &a=+0.309031 \quad &&b=+1.132747 \quad &&&c_0=+0.16510 \\ \nonumber&c_1=-0.82999 \quad &&c_2=+1.21782 \quad &&&c_3 =-0.54665 \\ \end{align}\]

добре підходить для кривої в межах (але не поза) діапазоном\(k_G = 0.15\text{ to }1.00\).