7.24: Правила вибору

Нагадаємо, що множник - це сукупність переходів між двома членами. Наприклад,\(^3 \text{P} − \ ^3 \text{D}^\text{o}\) це множник, що з'єднує два члени\(^3 \text{P}\) і\(^3 \text{D}^\text{o}\). Кожен член має три рівні, і тому існує дев'ять способів з'єднання рівнів одного члена з іншим, кожен перехід призводить до лінії. Але насправді лише шість таких переходів «дозволені» або «дозволені», решта три - «заборонені». Це пов'язано з певними «правилами відбору» або обмеженнями в тому, як деякі квантові числа можуть змінюватися. Так само існують обмеження на кількість множників, які можуть з'єднувати члени двох поліад, або на кількість компонентів Zeeman, які можуть з'єднувати стани двох рівнів. У всіх цих ситуаціях існують правила вибору, які обмежують зміну певних квантових чисел на інші, ніж певні суми. У цьому розділі ми спробуємо якісно розібратися, як виникають такі правила вибору. Ми перерахуємо різні правила вибору і подивимося, як це вплине на кількість рядків у мультиплеті або кількість компонентів у рядку.

Всім відомо, що коли електричний диполь коливається, він випромінює електромагнітну хвилю. Так само, якщо диполь, а не періодично коливається, раптом зазнає зміни свого електричного дипольного моменту - наприклад, якщо відстань між двома протилежними електричними зарядами раптово зміниться - буде випромінюватися імпульс електромагнітного випромінювання. У той час як випромінювання від одного атома буде випромінюватися, як у диполя, в газі з величезною кількістю атомів, орієнтованих у абсолютно випадкових напрямках, випромінювання буде виглядати ізотропним.

Один розумний спосіб пояснити, як атом випромінює імпульс (квант) електромагнітного випромінювання, коли він переходить з одного стану в інший, полягає в тому, що його дипольний момент змінюється, а випромінювана енергія пов'язана зі зміною його дипольного моменту. Дійсно, в квантовій механіці кількість енергії, що випромінюється при переході атома з одного стану в інший, визначається квадратом величини, відомої як перехідний момент:

\[\int \psi_f^* \boldsymbol{\mu} \psi_i d \tau . \]

Тут\(d\tau\) знаходиться звичайний елемент гучності, і\(\psi_I\) є хвильовою функцією початкового стану. \(\boldsymbol{\mu}\)оператор дипольного моменту, який залежить від положень всіх електронів в атомі. \(\psi^*_f\)є сполученням хвильової функції кінцевого стану. Ті, хто має багато практики у виконанні таких обчислень, достатньо досвідчені, щоб знати, що ефект оператора дипольного моменту полягає лише у створенні подібної хвильової функції з, можливо, деякими змінами квантових чисел. Тому, щоб зберегти виписання повного виразу для хвильової функції в повному обсязі, вони просто перераховують квантові числа початкової хвильової функції в кеті, і сполучених кінцевої функції в бюстгальтері, таким чином:

\[\langle L^\prime S^\prime J^\prime M^\prime | \boldsymbol{\mu} | LSJM \rangle . \]

Знову ж таки, ті, хто робить такі обчислення щодня для життя, незабаром визнають, з самої симетрії хвильових функцій (теорія груп) і не турбуючись сильно про деталі функцій, що цей перехідний момент дорівнює нулю, якщо не існує певних зв'язків між початковим і кінцевим квантом цифри. Саме ті переходи, які призводять до ненульового перехідного моменту, «дозволені». Якщо перехідний момент дорівнює нулю, яким він є за винятком певних комбінацій початкових і кінцевих квантових чисел, перехід «заборонений».

Наприклад, якщо ми обговорюємо можливі компоненти Зеемана рядка, єдиними «дозволеними» переходами - тобто єдиними ненульовими моментами переходу - це ті, у яких початкове та кінцеве значення\(M\) або рівні, або відрізняються на\(\pm 1\). Ми говоримо, що «правило вибору» для ефекту Зеемана є. \(\Delta M = 0, \ \pm 1\)Це обмеження ми вже врахували при малюванні цифр VII.1 і VII.2. У першому замість 15 можливих компонентів всього дев'ять з ненульовими моментами переходу і які задовольняють правилу вибору, а на малюнку VII.2 всього шість, а не вісім.

Власне, при спостереженні ефекту Зеемана, якщо ми розглядаємо світло з напрямку, перпендикулярного магнітному полю, ми бачимо, що компоненти з\(\Delta M = 0\) плоскі поляризовані паралельно магнітному полю, і називаються\(p\) -компонентами, а ті, з\(\Delta M = \pm 1\) - плоскі поляризовані перпендикулярно магнітному полю, і називаються\(s\) -складовими (німецький senkrecht - перпендикулярно). (Може здатися, що символи\(s\) і\(p\), особливо перші, зараз роблять більше, ніж їх справедлива частка роботи.) Якщо спектр розглядається з напрямку вздовж магнітного поля, буде виявлено, що\(s\) компоненти циркулярно поляризовані в протилежних сенсах, тоді як\(p\) -компоненти взагалі не видно.

Подібно до того, як кількість компонентів Zeeman\(\Delta M = 0, \pm 1\) у рядку обмежена правилом вибору аналогічним чином, кількість можливих рядків у мультиплеті обмежена правилом виділення\(\Delta J = 0, \pm 1\) (\(0 \leftrightarrow 0\)заборонено). Я вже згадував, що\(^3 \text{P} - \ ^3 \text{D}^\text{o}\) мультиплет має лише шість рядків, а не дев'ять. На малюнку VII.3 показані можливі переходи. (На відміну від цифр VII.1 і VII.2, в яких горизонтальна шкала була лінійною за довжиною хвилі зі збільшенням довжини хвилі вправо, горизонтальна шкала на малюнку VII.3 не має значення.)

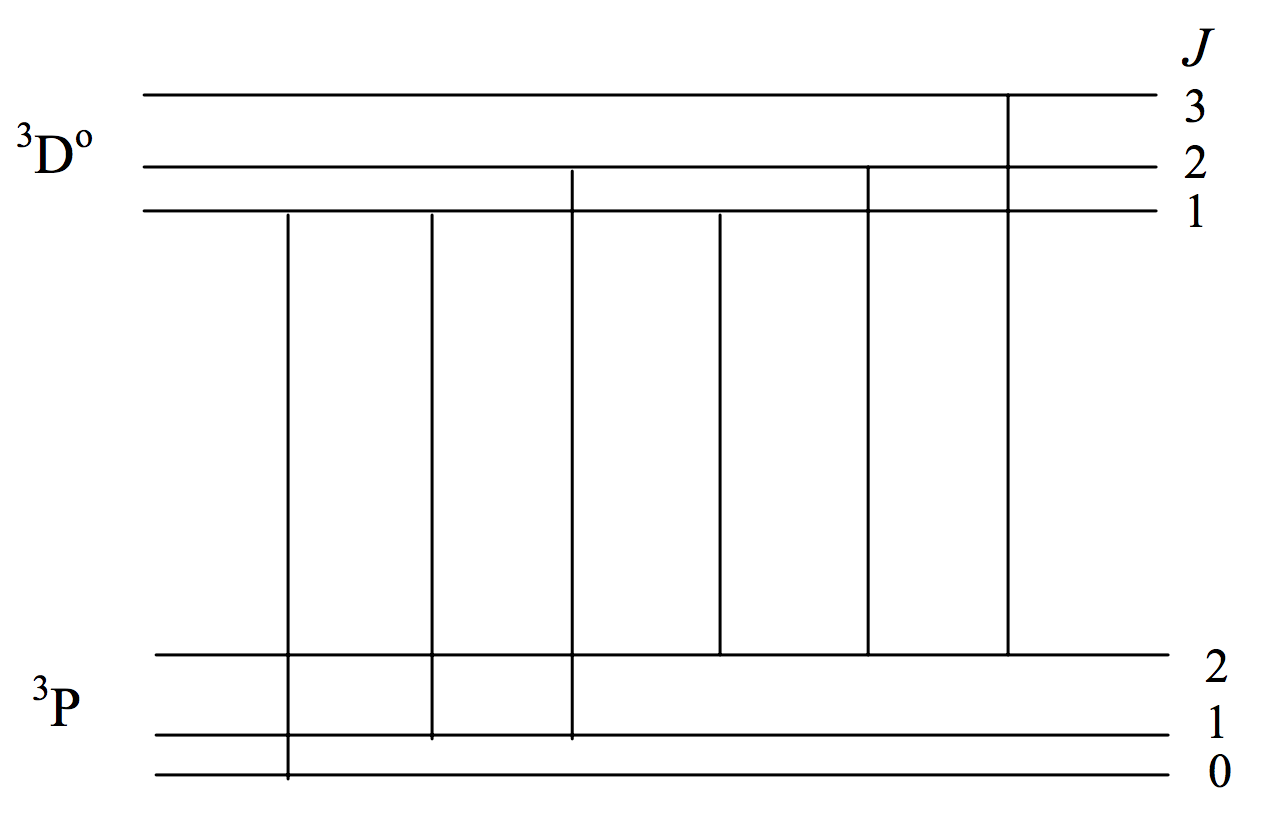
\(\text{FIGURE VII.3}\)

Можливо, лінія або компонент заборонено дипольне випромінювання і що, якщо μ є оператором електричного дипольного моменту, перехідний момент дорівнює нулю. Однак, якщо замінити оператор дипольного моменту оператором електричного квадрупольного або магнітного дипольного моменту, перехідний момент не дорівнює нулю. У цьому випадку перехід, заборонений до електричного дипольного (\(\text{E}1\)) випромінювання, може бути дозволений до електричного квадрупольного (\(\text{E}2\)) або магнітного дипольного (\(\text{M}1\)) випромінювання. \(\text{E}2\)і\(\text{M}1\) переходи дуже слабкі і рідко спостерігаються в лабораторних умовах (хоча вони відбуваються в астрономічних джерелах з причин, які будуть пояснені пізніше). Тому лінії, заборонені до електричного дипольного випромінювання, зазвичай називають просто «забороненими» лініями - навіть якщо вони насправді не заборонені\(\text{E}2\) або\(\text{M}1\) випромінювання. Носій (атом) для забороненої лінії часто пишеться в дужках. Наприклад, існує\(\text{E}2\) лінія в спектрі полярного сяйва при\(557.7 \ \text{nm}\) виникненні з нейтрального атома кисню, тому лінія, як кажуть, є лінією\([\text{O}_\text{ I}]\).

Деякі мультиплети заборонені до електричного дипольного випромінювання лише в тому випадку, якщо відповідні умови суворо відповідають\(LS\) -couplets, але можуть бути дозволені для електричного дипольного випромінювання, якщо є відхилення від\(LS\) -зв'язку. Такі переходи є «напівзабороненими», а носій іноді пишеться між дужкою і дужкою. При цьому виникає напівзаборонена лінія при\(345.3 \ \text{nm}\) обумовленій\([\text{Al}_\text{ I})\). Для\(LS\) -зчеплення електричне дипольне випромінювання допускається тільки в тому випадку, якщо\(\Delta S = 0\). Тобто, переходи допускаються між двома триплетними термінами або між двома синглетними термінами, але не між трійкою або синглет. (У зв'язку з цим я маю на увазі\(^3 \text{S}\) термін як термін «триплет», хоча він має лише один рівень.) Далеко не всі користуються цією дужкою-дужками конвенції.

У нейтральному атомі гелію є синглетні члени та триплетні члени. \(LS\)-зчеплення є нормою, і, через це, немає переходів між будь-яким з синглетних термінів і триплетним терміном. Дійсно, це так, ніби є два цілком незалежних множини термінів і два спектри, і дійсно синглетні терміни і триплетні терміни іноді називають «парагелієм» і «орто-гелієм» відповідно. За таких обставин важко (або неможливо за відсутності додаткових незалежних доказів) знати відносні енергії триплетного та синглетного термінів або знати, який є основним терміном атома - хоча тепер ми знаємо, що основний термін гелію є\(^3 \text{S}\) терміном.

Нейтральний кальцій також має набір синглетних термінів і набір триплетних термінів, але є відступи від\(LS\) -муфти, а є мультиплети, що з'єднують синглет з трійчастими термінами і навпаки. Такі мультиплети називаються «інтеркомбінованими» або «міжсистемними» мультиплетами. Наприклад, рядок at\(657.3 \ \text{nm}\) є членом\(^1 \text{S} − \ ^3 \text{P}^\text{o}\) множника\([\text{Ca}_\text{ I})\).

Ось список різних правил вибору, які я можу придумати. Я не включив ядерний спін, але ви можете зробити висновок, що правила, враховуючи, що зв'язок між електронним кутовим імпульсом і ядерним спіном, як правило, є чистим\(JI\) -зв'язком (аналог\(LS\) -couplation).

Для електричних дипольних переходів. Переходи відбуваються між термінами різної конфігурації, такі, що\(l\) -значення одного електрона має змінюватися на\(\pm 1\). Звідси випливає, що дозволені переходи знаходяться між умовами протилежного парності. Рядки всередині множника підпадають під дію правила вибору\(\Delta J = 0, \ \pm 1\), за винятком того, що\(0\)\(0\) заборонено. (Ці правила порушуються для електричного дипольного випромінювання при наявності сильного зовнішнього електричного поля, яке не повинно стосуватися нас тут, але потрібно враховувати щодо ефекту Старка.) Компоненти лінії Zeeman підпадають під дію правила вибору\(\delta M = 0, \pm 1\).

Для\(LS\) -зчеплення існують наступні додаткові обмеження. \(\Delta S = 0\); тобто міжсистемні переходи заборонені до електричного дипольного випромінювання. Вони «напівзаборонені». \(\Delta L = 0, \ \pm 1\), хіба\(0\) що\(0\) заборонено. Таким чином\(\text{S} − \ \text{S}^\text{o}\)\(\text{S} − \ \text{D}^\text{o}\),\(\text{P} − \ \text{F}^\text{o}\) мультиплети все б вказували на відхилення від\(LS\) -зчеплення. Переходи також повинні відбуватися між термінами спільного батьківства.

Для магнітних дипольних переходів. Переходи відбуваються між термінами єдиної конфігурації, а значить, і між умовами однакового парності. Рядки всередині множника підпадають під дію правила вибору\(\Delta J = 0, \ \pm 1\), за винятком того, що\(0\)\(0\) заборонено. Компоненти Zeeman рядка підпадають під дію правила вибору\(\Delta M = 0, \ \pm 1\), за винятком цього\(\Delta J\) і\(\Delta M\) не можуть бути нульовими.

Для\(LS\) -муфти є додаткові обмеження\(\Delta S = 0\) і\(\Delta L = 0\).

Для електричних квадрупольних переходів. Переходи відбуваються або між термінами однієї конфігурації, або між конфігураціями, в яких\(l\) -значення одного електрона змінюється на\(\pm 2\). У будь-якому випадку це означає, що переходи відбуваються між термінами однакового паритету. Рядки всередині множника підпадають під дію правила вибору\(\Delta J = 0, \ \pm 1, \ \pm 2\), крім цього\(0-0, \ \frac{1}{2}-\frac{1}{2}, \ 0-1\) і\(1-0\) заборонені. Це означає, що\(J^\prime + J^{\prime \prime}\) повинно бути хоча б\(2\). Компоненти лінії Zeeman підпадають під дію правила вибору\(\Delta M = 0, \ \pm 1, \ \pm 2\).

Для\(LS\) -муфти є додаткові обмеження\(\Delta S = 0\) і\(\Delta L = 0, \ \pm 1, \ \pm 2\), крім того,\(\Delta L = 0-0, \ 0-1, \ 1-0\) заборонені. Переходи також повинні відбуватися між термінами спільного батьківства.

Вправа. У розділі 7.16 я перерахував перші десять рівнів для атома водню - тобто рівні в перших трьох оболонках. Я також стверджував, що Hα містить три перехідні масиви, три множники, сім рядків і невизначену кількість компонентів Zeeman. Тепер, коли ви знайомі з правилами вибору, ви можете переконатися в цьому. Тому в якості вправи перерахуйте всі масиви, мультиплети та рядки, що містять\(\text{H}\alpha\). (Ви повинні припустити\(LS\) -зв'язок; очевидно, тільки з одним електроном немає різниці між\(LS\) - і\(jj\) -муфтою.) Наприклад,\(2p − 3d\) це один масив. \(2p \ ^2\text{P}^\text{o} - 3d \ ^2\text{D}\)є мультиплетом. \(2p \ ^2\text{P}_{\frac{3}{2}}^\text{o} - 3d \ ^2\text{D}_\frac{5}{2}\)є лінією. У таблиці в розділі 7.16 я перерахував статистичну вагу кожного рівня. Для кожного рівня перерахуйте можливі\(M\) значення, а потім, використовуючи правила вибору Zeeman, визначте, скільки компонентів Zeeman існує для кожного рівня, а значить і для в\(H\alpha\) цілому. Скільки компонентів Zeeman мають різні довжини хвиль?

У вищевказаній вправі, можливо, ви проігнорували ефект ядерного спина. Тепер включаємо ядерний спін (\(I = 1/2\)). Тепер ви побачите, що кожен з восьми рівнів, що беруть участь у формуванні,\(\text{H}\alpha\) розділений на два надтонких рівня з різними значеннями\(F\). Тепер, скільки там надтонкого і Зеємана?

Тепер відповімо на ті ж питання з дейтерієм. Можна сподіватися, що ядро дейтерію («дейтрон») має нульовий ядерний спін - але такої удачі немає, бо спина дейтрона є\(I = 1\). При цьому більшість рівнів складаються з трьох надтонких рівнів. (Чому я сказав «більшість»? Деякі з рівнів мають тільки два надтонких рівнів, чи не так? Розумієте чому?) Скільки надтонких і Zeeman компонентів дозволено правилами вибору?

Звичайно, природний водень включає\(^1 \text{H}\) і те, і інше, і дуже невелика кількість\(^2 \text{H}\), і спектри обох будуть виставлені. Воістину\(\text{H}\alpha\) це набагато складніша «лінія», ніж ми передбачали в розділі 7.3! Щоб додати до ускладнення, не можна забувати, що в земних умовах водень є молекулярним, і існує три можливих ізотопомери -\(\text{H}_2, \ \text{HD}\) і\(\text{D}_2\) - і ті, хто знайомий з молекулярними спектрами, нагадають, що існують очевидні відмінності між спектрами гомоядерних і гетероядерні молекули. Можна було б чітко витратити все життя, вивчаючи спектр водню!