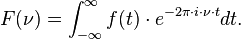Skip to main content
LibreTexts - Ukrayinska

32.10: Аналіз Фур'є

  1. Last updated
  2. Save as PDF
  • Page ID
    26770

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Перетворення Фур'є перетворює функцію проти безперервного (або декретування) часу і відображає її у функцію проти безперервних (або декретованих) частот. Отже, перетворення перетворює дані часової області в дані частотної області (і навпаки). Таке розкладання функції на синусоїди різної частоти є потужним підходом до багатьох експериментальних і теоретичних завдань. Спектроскопія перетворення Фур'є - це підхід, за допомогою якого спектри збираються на основі вимірювань за допомогою вимірювань у часовій області або космічній області електромагнітного випромінювання або іншого типу випромінювання. Він може бути застосований до різних типів спектроскопії, включаючи оптичну спектроскопію, інфрачервону спектроскопію (FT IR, FT-NIRS), перетворення Фур'є ядерного магнітного резонансу (ЯМР), мас-спектрометрії та спектроскопії електронного спінового резонансу.

    Вступ

    Аналіз Фур'є є предметною областю, яка виросла в результаті вивчення рядів Фур'є. Суб'єкт почав з спроби зрозуміти, коли можна було представляти загальні функції сумами більш простих тригонометричних функцій. Спроба зрозуміти функції (або інші об'єкти), розбивши їх на основні частини, які легше зрозуміти, є однією з центральних тем аналізу Фур'є. Аналіз Фур'є названий на честь Джозефа Фур'є, який показав, що представлення функції тригонометричним рядом значно спростило вивчення поширення тепла. Сьогодні предмет аналізу Фур'є охоплює широкий спектр математики з частинами, які, на перший погляд, можуть здатися зовсім іншими. У науках і техніці процес розкладання функції на більш прості шматки часто називають аналізом. У аналізі Фур'є термін перетворення Фур'є часто відноситься до процесу, який розкладає задану функцію на основні частини. Цей процес призводить до іншої функції, яка описує, скільки кожного основного фрагмента знаходиться в оригінальній функції. Однак перетворенню часто дається більш конкретна назва залежно від області та інших властивостей трансформується функції, як описано нижче. Більше того, оригінальна концепція аналізу Фур'є була розширена з часом, щоб застосовуватися до все більш абстрактних та загальних ситуацій, а загальне поле часто називають гармонічним аналізом.

    Серія Фур'є

    Коли функція ƒ є функцією часу і являє собою фізичний сигнал, перетворення має стандартну інтерпретацію як частотний спектр сигналу. Величина результуючої комплекснозначної функції F на частоті ω представляє амплітуду частотної складової, початкова фаза якої задається фазою F. Однак важливо усвідомлювати, що перетворення Фур'є не обмежуються функціями часу, а часовими частотами. Вони однаково можуть бути застосовані для аналізу просторових частот, і справді майже для будь-якої функціональної області.

    Властивості

    http://www.math.ubc.ca/~feldman/demos/demo3.html

    Безперервна трансформація Фур'є (CFT)

    Найчастіше некваліфікований термін перетворення Фур'є відноситься до перетворення функцій неперервного дійсного аргументу, наприклад часу (t). У цьому випадку перетворення Фур'є описує функцію ƒ (t) через основні комплексні експоненціальні показники різних частот. У терміні звичайної частоти ν перетворення Фур'є задається комплексним числом:

    F (\ nu) =\ int_ {-\ infty} ^ {\ infty} f (t)\ cdot e^ {- 2\ пі\ cdot i\ cdot\ nu\ cdot t} дт.

    Оцінювання цієї величини для всіх значень φ дає функцію частотної області.

    Дискретне перетворення Фур'є (DFT)

    Експериментально ми збираємо дані, які не є безперервними, але вибірки вимірювань у певній точці. Отже, ми маємо справу з дискретною версією перетворення Фур'є.

    Швидка передача Фур'є (FFT)

    Дискретну версію перетворення Фур'є (див. Нижче) можна швидко оцінити на комп'ютерах з використанням алгоритмів швидкого перетворення Фур'є (БПФ). Цей алгоритм, як правило, вимагає 2 n кількість вимірювань для роботи. Отже, ви помітите набори даних часто з такими розмірами. (Конте & де Бур 1980)

    Посилання

    1. Арфкен, Г. «Серія Фур'є». Гл. 14 з математичних методів для фізиків, 3-е изд. Орландо, Флорида: Академічна преса, с. 760-793, 1985.
    2. Askey, R. і Haimo, D.T. «Подібності між Фур'є і силовими рядами». Амер. Математика. Щомісячно 103, 297-304, 1996.
    3. Байєр, В.Х. (ред.). Стандартні математичні таблиці CRC, 28-е видання. Бока-Ратон, Флорида: CRC Press, 1987.
    4. Браун, Дж. В. та Черчілль, Ряди Р.В. Фур'є та крайові задачі, 5-е видання. Нью-Йорк: Макгроу-Хілл, 1993.
    5. Байерлі, В.Е. Елементарний трактат про ряди Фур'є та сферичні, циліндричні та еліпсоїдні гармоніки з додатками до задач математичної фізики. Нью-Йорк: Дувр, 1959.
    6. Карслав, Г.С. Вступ до теорії рядів Фур'є та інтегралів, 3-е изд., ред. та ін. Нью-Йорк: Дувр, 1950.
    7. Девіса, Г. Ф. Фур'є та ортогональні функції. Нью-Йорк: Дувр, 1963.
    8. Дим, Х. і Маккін, Н. П. серії Фур'є та інтеграли. Нью-Йорк: Академічна преса, 1972.
    9. Фолланд, Г.Б. аналіз Фур'є та його застосування. Пасифік-Гроув, Каліфорнія: Брукс/Коул, 1992.
    10. Геометричні застосування рядів Фур'є та сферичних гармонік. Нью-Йорк: Кембриджський університетський прес, 1996.
    11. Корнер, Т.В. аналіз Фур'є. Кембридж, Англія: Кембриджський університетський прес, 1988.
    12. Körner, T.W. Вправи для аналізу Фур'є. Нью-Йорк: Кембриджський університетський прес, 1993.
    13. Кранц, С.Г. «Серія Фур'є». §15.1 у Довіднику комплексних змінних. Бостон, Массачусетс: Біркхойзер, стор. 195-202, 1999.
    14. Лайтхілл, М.Дж. Вступ до аналізу Фур'є та узагальнених функцій. Кембридж, Англія: Кембриджський університетський прес, 1958.
    15. Моррісон, Н. Вступ до аналізу Фур'є. Нью-Йорк: Вілі, 1994.
    16. Сансоне, Г. «Розширення в рядах Фур'є». Гл. 2 в Ортогональні функції, ред. англ. Нью-Йорк: Дувр, стор. 39-168, 1991.
    17. Вайштайн, Е. «Книги про перетворення Фур'є». http://www.ericweisstein.com/encyclopedias/books/FourierTransforms.html.
    18. Віттакер, Е.Т. і Робінсон, Г. «Практичний аналіз Фур'є». Гл. 10 в Обчислення спостережень: Трактат з обчислювальної математики, 4-е изд. Нью-Йорк: Дувр, стор. 260-284, 1967.
    19. Спектроскопія Р.Р. Вільямса та перетворення Фур'є Вілі: Нью-Йорк, 1995
    20. Беттіс, Кліфф; Лайонс, Едвард Дж.; Брукс, Девід Дж. Чем. Освіта. 1996, 73, 839
    21. Графф, Дар'я К.Дж. Едук. 1995, 72, 304.
    22. Чесик, Джон П.Дж. Chem. Освіта. 1989, 66, с 128.
    23. Глассер, Л.Дж. Едук. 1987, 64, А228.
    24. Глассер, Л.Ю. Едук. 1987, 64, А255.
    25. Глассер, Л.Дж. Едук. 1987, 64, А306.

    Автори та атрибуція

    • Запис у Вікіпедії (на початку)
    • MMRC.Caltech.edu/FTIR/FTIR інтро.pdf