Skip to main content
LibreTexts - Ukrayinska

15.1: Вступ

  1. Last updated
  2. Save as PDF
  • Page ID
    74837

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Контрастні механічні та електромагнітні хвилі

    Огляд

    Хвиля - це коливання, яке рухається через простір, супроводжується передачею енергії. Хвильовий рух передає енергію з однієї точки в іншу, часто без постійного зміщення частинок середовища - тобто з невеликим або зовсім відсутнім пов'язаним масовим транспортом. Вони складаються, замість цього, з коливань або вібрацій навколо майже нерухомих місць. Існує два основних типи хвиль. Механічні хвилі поширюються через середовище, і речовина цього середовища деформується. Деформація змінює себе завдяки відновлювальним зусиллям, що виникають внаслідок її деформації.

    Другий основний тип хвиль, електромагнітні хвилі, не вимагають середовища (хоча вони все ще можуть поширюватися через середовище). Натомість вони складаються з періодичних коливань в електричних та магнітних полах, що генеруються зарядженими частинками, і тому можуть подорожувати через вакуум.

    Хвильове рівняння

    Форма хвилі може приймати форму будь-якої функції, яка повторюється над якоюсь характерною просторовою шкалою λλ, довжиною хвилі (див.). Більш загально, форми хвиль - це скалярні функції uu, які задовольняють хвильовому рівнянню,\(\mathrm{\frac{∂^2u}{∂t^2}=c^2∇^2u}\). Це рівняння просто стверджує, що прискорення форми хвилі (Ліва: друга похідна по відношенню до часу) пропорційно Лапласиану (Праворуч: друга просторова похідна) тієї ж форми хвилі. Константа пропорційності\(\mathrm{c^2}\),, - квадрат швидкості поширення хвилі.

    зображення

    Загальні форми хвиль: Зразок декількох поширених, простих форм хвиль. Форма хвилі - це функція, яка повторюється в просторі.

    Синусоїда

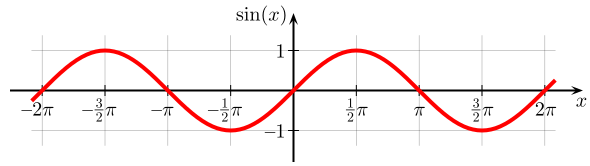
    зображення

    Ділянка синуса: Функція синуса, графічна на декартовій площині. На цьому графіку кут x задається в радіанах (π = 180°).

    Розглянемо одну з найпоширеніших форм хвиль, синусоїду. Загальна форма синусоїдальної хвилі - це\(\mathrm{y(x,t)=A \sin (kx−ωt+ϕ)}\), де A - амплітуда хвилі,\(\mathrm{ω}\) - кутова частота хвилі, k - хвильове число, і\(\mathrm{ϕ}\) є фазою синусоїдальної хвилі, заданої в радіанах. Ця форма хвилі дає положення переміщення («y») частинки в середовищі від її рівноваги як функція як положення «x», так і часу «t».

    Беручи похідні, очевидно, що наведене вище хвильове рівняння має значення\(\mathrm{c=\frac{ω}{k}}\), що також називається фазовою швидкістю хвилі. Щоб знайти швидкість частинки в середовищі при x і t, ми беремо тимчасову похідну форми хвилі, щоб отримати\(\mathrm{∂y(x,t)∂t=−Aω \cos (kx−ωt+ϕ)}\). Аналогічно, щоб знайти прискорення зміщеної частинки в середовищі при x і t, ми беремо другу похідну, щоб отримати\(\mathrm{\frac{∂^2y(x,t)}{∂t^2}=−Aω^2 \sin (kx−ωt+ϕ)}\). Зверніть увагу на фазову залежність між тригонометричними функціями в\(\mathrm{y(x,t), y'(x,t), y”(x,t)}\). Коли зміщення частинок максимальне або мінімальне, швидкість дорівнює 0. Коли зміщення дорівнює 0, швидкість частинок або максимальна, або мінімальна. Аналогічно, прискорення частинок є максимальним (або мінімальним), коли зміщення частинок є мінімальним (або максимальним) відповідно.

    Довільна хвиля

    Ми уважно подивилися в синусоїдальну хвилю. Але як щодо хвиль, що має загальну форму? Одним з важливих аспектів хвильового рівняння є його лінійність: хвильове рівняння є лінійним у u і залишається незмінним при перекладах у просторі та часі. Оскільки хвиля з довільною формою може бути представлена сумою багатьох синусоїдальних хвиль (це називається аналіз Фур'є), ми можемо генерувати безліч розв'язків хвильового рівняння шляхом перекладу та підсумовування синусоїдальних хвиль, які ми тільки що уважно розглянули.

    Ключові моменти

    • Хвильове рівняння вимагає, щоб друга похідна за часом форми хвилі була пропорційною її другій просторовій похідній.
    • Форми хвиль описують форму фізичних хвиль і можуть приймати форму будь-якої функції, яка повторюється в просторі.
    • Однією з найпоширеніших форм хвиль у фізиці є синусоїда. Оскільки будь-яка арбітражна форма хвилі може бути сформована шляхом додавання набору синусоїдальних хвиль, фізика, яка керує хвилею довільної форми, може бути описана за допомогою її синусоїдальних компонентів.

    Ключові умови

    • форма хвилі: форма фізичної хвилі, такої як звук або електромагнітне випромінювання. Форма може бути будь-якою функцією, яка повторюється в просторі.
    • Аналіз Фур'є: Вивчення того, як загальні функції можуть бути представлені або апроксимовані сумами простих тригонометричних функцій.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ