6.4: Атомні орбіталі водню залежать від трьох квантових чисел
- Page ID
- 27368
- Визнайте, як атомні орбіталі водню змінюються як функція трьох первинних квантових чисел
Розв'язки рівняння атома водню Шредінгера, розглянуті раніше, є функціями, які є добутком сферичної гармонічної функції та радіальної функції.
\[ \psi _{n, l, m_l } (r, \theta , \varphi) = \underbrace{R_{n,l} (r)}_{radial} \underbrace{ Y^{m_l}_l (\theta , \varphi)}_{angular} \label {6.1.14} \]
Хвильові функції атома водню залежать від трьох змінних\(r\)\(\theta\),\(\varphi \) і трьох квантових чисел\(n\)\(l\), і\(m_l\). Змінні дають положення електрона щодо протона в сферичних координатах. Абсолютний квадрат хвильової функції\(| \psi (r, \theta , \varphi )|^2\), оцінюється при\(r\)\(\theta \), і\(\varphi\) дає щільність ймовірності знаходження електрона всередині диференціального об'єму\(d \tau\), центрованого в положенні\(r\), заданому\(\theta \), і\(\varphi\).
Оцініть наступні інтеграли
- \( \langle \psi (r, \theta, \varphi )| \psi (r, \theta , \varphi ) \rangle \nonumber\)
- \( \langle \psi (r, \theta, \varphi )| \psi (r', \theta' , \varphi' ) \rangle \nonumber\)
- Відповідь
-
а Цей інтеграл дорівнює одиниці, оскільки\(\psi(r, \theta, \varphi)\) є нормованими власними станами.
b Однак ми можемо явно оцінити цей інтеграл для будь-якої довільної пари власних станів
\[\begin{align*} \langle\psi(r,\theta,\varphi)|\psi(r',\theta',\varphi')\rangle & = \int\limits_{all space}\psi^*(r,\theta,\varphi)\psi(r',\theta',\varphi')d\tau \\[4pt] &=\int\limits_{0}^{\infty} dr \int\limits_{0}^{\pi}d\theta\int\limits_{0}^{2\pi}d\varphi(r^2\sin(\theta))\overbrace{\psi*(r,\theta,\varphi)}^{R_{n,l}(r)Y_{l}^{m_l}(\theta,\varphi)}\overbrace{\psi(r,\theta,\varphi)}^{R_{n',l'}(r)Y_{l'}^{m'_l}(\theta,\varphi)} \\[4pt] &=\int \limits_{0}^{\infty} dr \int\limits_{0}^{\pi}d\theta \int \limits_{0}^{2\pi} d\varphi(r^2\sin(\theta))[R_{n,l}(r)Y_{l}^{m_l}(\theta,\varphi)][R_{n',l'}(r)Y_{l'}^{m'_l}(\theta,\varphi)] \\[4pt] &=\left[\int\limits_{0}^{\infty}r^2[R_{n,l}(r)R_{n',l'}(r)]dr\right]\left[\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\sin(\theta)[Y_{l}^{m_l}(\theta,\varphi)Y_{l'}^{m'_l}(\theta,\varphi)]d\theta d\varphi \right] \\[4pt] &=\langle R_{n,l}(r)|R_{n',l'}(r)\rangle\langle Y_{l}^{m_l}(\theta,\varphi)|Y_{l'}^{m'_l}(\theta,\varphi)\rangle \\[4pt] &=(\delta_{nn'}\delta_{ll'})(\delta_{ll'}\delta_{mm'}) =\delta_{nn'}\delta_{ll'}\delta_{mm'} \end{align*} \nonumber \]
Хоча частина a демонструє нормальність власних станів, частина b демонструє ортогональність власного стану (і нормальність теж).
Квантові числа мають назви:
- \(n\)називається основним квантовим числом,
- \(l\)називається квантовим числом моменту моменту, і
- \(m_l\)називається магнітним квантовим числом, оскільки енергія в магнітному полі залежить від\(m_l\).
Часто\(l\) називають азимутальним квантовим числом, оскільки воно є наслідком\(\theta\) -рівняння, яке передбачає азимутальний кут\(\Theta \), що відноситься до кута до зеніту.
Радіальна частина хвильової функції
Асимптотична поведінка (тобто далеко від ядра) до радіальної частини хвильової функції є
\[ R_{asymptotic} (r) \sim \exp \left(-\dfrac {r}{n} a_0 \right) \label {6.1.15} \]
де\(n\) вийде квантове число і\(a_0\) - радіус Бора (~52,9 пм). Зауважте, що ця функція зменшується експоненціально з відстанню, подібно до загасаючої експоненціальної частини хвилевих функцій гармонічного генератора, але з різною залежністю відстані,\(r\) проти\(r^2\).
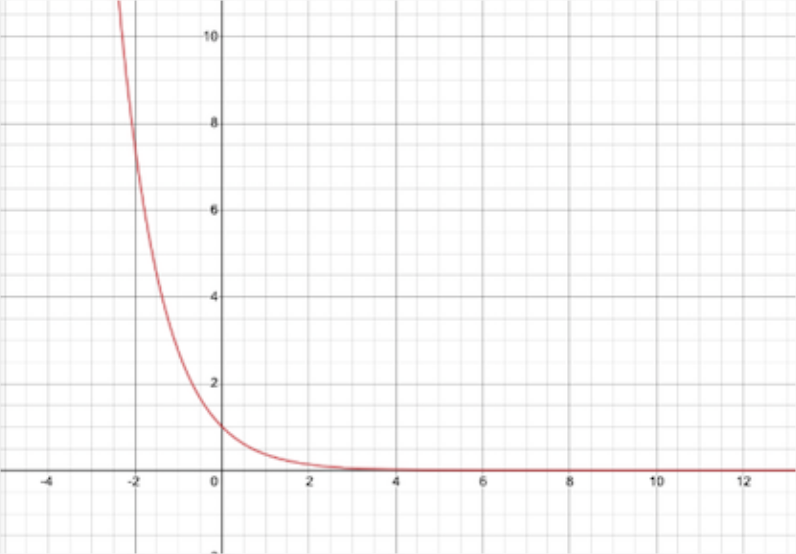
Що відбувається з величиною, коли відстань\(r\) від протона наближається до нескінченності?\(R_{asymptotic}(r)\) Намалюйте графік функції,\(R_{asymptotic}(r)\). Чому таку поведінку можна очікувати для електрона в атомі водню?
- Відповідь
-
\[R(r)=e^{-\frac{c}{n} a_{0}} \nonumber \]
Коли\(r\) наближається нескінченність, експоненціальний розпад йде до нуля, цього слід очікувати, оскільки ймовірність виявлення електрона на нескінченній відстані теж майже дорівнює нулю.
Поліноми, одержувані усіченням степеневих рядів, пов'язані з асоційованими поліномами Лагерра\(L_n , _l(r)\), де множиною\(c_i\) є постійні коефіцієнти.
\[L_{n, l} (r) = \sum _{r=0}^{n-l-1} c_i r^i \label {6.1.16} \]
Ці многочлени ідентифікуються двома індексами або квантовими числами,\(n\) і\(l\). Фізично прийнятні рішення вимагають, що\(n\) повинно бути більше або дорівнює\(l +1\). Найменше значення для\(l\) дорівнює нулю, тому найменше значення для\(n\) дорівнює 1. Квантове число моменту моменту впливає на розв'язання радіального рівняння, оскільки воно з'являється в радіальному диференціальному рівнянні (Equation\(\ref{6.1.14}\)).
\(R(r)\)Функції, що вирішують радіальне диференціальне рівняння\(\ref{6.1.14}\), є добутками асоційованих поліномів Лагерра і експоненціального коефіцієнта, помноженого на коефіцієнт нормалізації\((N_{n,l})\) і\(\left (\dfrac {r}{a_0} \right ) ^l\).
\[R (r) = N_{n,l} \left ( \dfrac {r}{a_0} \right ) ^l L_{n,l} (r) e^{-\frac {r}{n {a_0}}} \label {6.1.17} \]
Убуваючий експоненціальний член переповнює зростаючий поліноміальний член так, що загальна хвильова функція проявляє бажане наближення до нуля при великих значеннях\(r\). Перші шість радіальних функцій наведено у таблиці Template:index. Відзначимо, що функції в таблиці виявляють залежність від того\(Z\), атомного номера ядра. Як обговорювалося далі в цьому розділі, інші електронні системи мають електронні стани, аналогічні тим, що для атома водню, і включення заряду на ядрі дозволяє використовувати ті ж хвильові функції для всіх одноелектронних систем. Для водню,\(Z = 1\).
|
|
|
|
|---|---|---|
| 1 | \ (l\)» style="вертикальне вирівнювання: середина; "> 0 | \ (R_ {n, l} (\ rho)\)» style="вертикальне вирівнювання: середина; ">\(2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\rho}\) |
| 2 | \ (l\)» style="вертикальне вирівнювання: середина; "> 0 | \ (R_ {n, l} (\ rho)\)» style="вертикальне вирівнювання: середина; ">\( \dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \rho) e^{-\rho/2}\) |
| 2 | \ (l\)» style="вертикальне вирівнювання: середина; "> 1 | \ (R_ {n, l} (\ rho)\)» style="вертикальне вирівнювання: середина; ">\( \dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \rho e^{-\rho/2}\) |
| 3 | \ (l\)» style="вертикальне вирівнювання: середина; "> 0 | \ (R_ {n, l} (\ rho)\)» style="вертикальне вирівнювання: середина; ">\( \dfrac {2}{81 \sqrt {3}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (27 - 18 \rho + 2\rho ^2) e^{-\rho/3}\) |
| 3 | \ (l\)» style="вертикальне вирівнювання: середина; "> 1 | \ (R_ {n, l} (\ rho)\)» style="вертикальне вирівнювання: середина; ">\( \dfrac {1}{81 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (6 \rho + \rho ^2) e^{-\rho/3}\) |
| 3 | \ (l\)» style="вертикальне вирівнювання: середина; "> 2 | \ (R_ {n, l} (\ rho)\)» style="вертикальне вирівнювання: середина; ">\( \dfrac {1}{81 \sqrt {30}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \rho ^2 e^{-\rho/3}\) |
Обмеження, яке\(n\) більше або дорівнює,\(l +1\) також виявляється квантованим енергією, створюючи той самий квантований вираз для рівнів енергії атома водню, який був отриманий з моделі Бора атома водню.
\[ E_n = - \dfrac {\mu e^4}{8 \epsilon ^2_0 h^2 n^2} \nonumber \]
Цікаво порівняти результати, отримані при розв'язанні рівняння Шредінгера, з моделлю Бора атома водню. Існує кілька способів, якими відрізняються моделі Schrödinger і Bohr.
- По-перше, і, мабуть, найбільш вражаюче, модель Шредінгера не виробляє чітко визначених орбіт для електрона. Хвильові функції лише дають нам ймовірність того, що електрон знаходиться в різних напрямках і відстанях від протона.
- По-друге, квантування моменту моменту відрізняється від запропонованого Бором. Бор запропонував, щоб кутовий імпульс квантувався в цілих одиницях\(\hbar\), тоді як модель Шредінгера призводить до моменту моменту моменту\( \sqrt{(l (l +1)} \hbar\).
- По-третє, квантові числа з'являються природним чином під час розв'язання рівняння Шредінгера, тоді як Бору довелося постулювати існування квантованих енергетичних станів. Хоча більш складна, модель Шредінгера призводить до кращої відповідності між теорією та експериментом у діапазоні застосувань, які були неможливі для моделі Бора.
Поясніть, як рівняння Шредінгера призводить до висновку, що кутовий момент атома водню може дорівнювати нулю, і поясніть, як існування таких станів з нульовим моментом моменту суперечить ідеї Бора про те, що електрон обертається навколо протона в атомі водню.
Три квантові числа
Ці квантові числа мають специфічні значення, які продиктовані фізичними обмеженнями або граничними умовами, накладеними на рівняння Шредінгера: n має бути цілим числом, більшим за 0,\(l\) може мати значення від 0 до\(n‑1\) і\(m_l\) можуть мати\(2l + 1\) значення в діапазоні від\(-l\) ‑ до \(+l\)в одиничних або цілих кроках. Значення квантового числа\(l\) зазвичай кодуються буквою: s означає 0, p означає 1, d означає 2, f означає 3; наступні коди тривають за алфавітом (наприклад, g означає\(l = 4\)). Квантові числа визначають квантування фізичних величин. Дискретні енергії різних станів атома водню задаються n, величина моменту моменту задається\(l\), а одна складова моменту моменту (зазвичай вибирається хіміками як z‑компонент) задається\(m_l\). Загальна кількість орбіталей з певним значенням\(n\) є\(n^2\).
Розглянемо кілька значень для\(n\), і показати, що кількість орбіталей для кожного\(n\) є\(n^2\).
Побудувати таблицю, що підсумовує допустимі значення для квантових чисел\(n\)\(l\), а\(m_l\) для енергетичних рівнів 1 - 7 водню.
Позначення 3d визначає квантові числа для електрона в атомі водню. Які значення для\(n\) і\(l\)? Які значення мають енергія і кутовий імпульс? Які можливі значення для магнітного квантового числа? Які можливі орієнтації вектора кутового моменту?