1.4: Рухи вільних частинок у більших розмірах
- Page ID
- 18960
Кількість розмірів залежить від кількості частинок і кількості просторових (та інших) розмірів, необхідних для характеристики положення і руху кожної частинки. Кількість вимірів також впливає на кількість квантових чисел, які можуть бути використані для позначення власних станів гамільтоніана.
Рівняння Шредінгера
Розглянемо електрон маси m і заряду, що\(e\) рухається по двовимірній поверхні, яка визначає\(x,y\) площину (наприклад, можливо, електрон обмежений поверхнею твердого тіла потенціалом, який щільно пов'язує його з вузькою областю в\(z\) -напрямку, але дозволяє йому бродити вільно над прямокутною площею в\(x,y\) площині), і припустити, що електрон відчуває постійний і не змінюється в часі потенціал\(V_0\) у всіх точках цієї площини. Наприклад, якщо\(V_0\) негативний, він може відображати енергію зв'язку електрона щодо його енергії у вакуумі.
Відповідне незалежне від часу рівняння Шредінгера:
\[- \dfrac{\hbar^2}{2m} \left(\dfrac{\partial^2}{\partial x^2} +\dfrac{\partial^2}{\partial y^2}\right)\psi(x,y) +V_0 \psi(x,y) = E\psi(x,y).\]
Завдання, що стоїть перед вами - розв'язати вищевказане рівняння власного значення для визначення дозволених енергетичних станів для цього електрона. Оскільки в цьому рівнянні немає термінів, які поєднують рух у\(y\) напрямках\(x\) і (наприклад, жодних термінів форми\(x^ay^b\) або\(x\dfrac{\partial}{\partial y}\) або\(\psi\dfrac{\partial}{\partial x}\)), поділ змінних може бути використаний для запису\(y\) як добутку\(\psi(x,y)=A(x)B(y)\). Заміна цієї форми в рівняння Шредінгера з подальшим збором всіх\(x\) -залежних і всіх y-залежних членів, дає;
\[- \dfrac{\hbar^2}{2m} \frac{1}{A}\frac{\partial^2 A}{\partial x^2} - \dfrac{\hbar^2}{2m} \frac{1}{B}\frac{\partial^2 B}{\partial y^2} = E-V_0.\]
Оскільки перший член не містить\(y\) -залежності, а другий не містить\(x\) -залежності, і тому, що права частина рівняння не залежить від обох\(x\) і\(y\), обидва члени зліва насправді повинні бути постійними (ці дві константи позначаються\(E_x\) і\(E_y\), відповідно, розуміючи, що у них є одиниці енергії). Це спостереження дозволяє записати два окремих рівняння Шредінгера:
\[- \dfrac{\hbar^2}{2m} \frac{1}{A}\frac{\partial^2 A}{\partial x^2} = E_x\]
і
\[- \dfrac{\hbar^2}{2m} \frac{1}{B}\frac{\partial^2 B}{\partial y^2} = E_y.\]
Потім загальна енергія\(E\) може бути виражена в терміні цих окремих енергій\(E_x\) і\(E_y\) від\(E_x + E_y = E-V_0\). Рішення рівнянь\(x-\)\(y-\) Шредінгера та Шредінгера легко бачити:
\[A(x) = \exp\left(ix\sqrt{\frac{2mE_x}{\hbar^2}}\right) \text{and} \exp\left(-ix\sqrt{\frac{2mE_x}{\hbar^2}}\right)\]
\[B(y) = \exp\left(iy\sqrt{\frac{2mE_y}{\hbar^2}}\right) \text{and} \exp\left(-iy\sqrt{\frac{2mE_y}{\hbar^2}}\right).\]
Для кожного рівняння отримано два незалежні розв'язки, оскільки рівняння\(x-\) Шредінгера та\(y-\) простір є диференціальними рівняннями другого порядку (тобто диференціальне рівняння другого порядку має два незалежні розв'язки).
граничні умови
Граничні умови, а не рівняння Шредінгера, визначають, чи будуть власні значення дискретними або неперервними
Якщо електрон повністю не обмежений всередині\(x,y\) площини, то енергії\(E_x\) і\(E_y\) можуть приймати будь-які значення; це означає, що експериментатор може вводити електрон на\(x,y\) площину з будь-якою сумарною енергією\(E\) і будь-якими складовими\(E_x\) і\(E_y\) вздовж двох осі до тих пір, поки\(E_x + E_y = E\). У такій ситуації можна говорити про енергії вздовж обох координат як знаходяться в континуумі або не квантовані.
На відміну від цього, якщо електрон обмежений залишатися в межах фіксованої області в\(x,y\) площині (наприклад, прямокутної або круглої області), то ситуація якісно інша. Обмеження електрона будь-якою такою заданою областю породжує граничні умови, що пред'являють додаткові вимоги до вищезазначених\(A\) і\(B\) функцій. Ці обмеження можуть виникнути, наприклад, якщо потенціал\(V(x,y)\) стає дуже великим для\(x,y\) значень за межами області, в цьому випадку ймовірність знаходження електрона за межами області дуже мала. Такий випадок може представляти, наприклад, ситуацію, коли молекулярна структура твердої поверхні змінюється поза замкнутою областю таким чином, що сильно відштовхує електрон (наприклад, як у випадку молекулярних коралів на металевих поверхнях). Потім цей випадок може представляти просту модель так званих коралів, в якій частка обмежена кінцевою областю простору.
Наприклад, якщо рух обмежено відбуватися в межах прямокутної області, визначеної\(0 \le x\le L_x\);\(0 \le y\le L_y\), то властивість неперервності, якій повинні підкорятися всі хвильові функції (через їх інтерпретацію як щільності ймовірності, яка повинна бути безперервною) призводить\(A(x)\) до зникнення при 0 і при \(L_x\). Тобто, тому що\(A\) повинні зникнути\(x < 0\) і повинні зникнути для\(x > L_x\), а тому, що\(A\) є безперервним, він повинен зникати в\(x = 0\) і при\(x = L_x\). Аналогічним чином,\(B(y)\) повинні зникнути при 0 і в\(L_y\). Щоб реалізувати ці обмеження для\(A(x)\), потрібно лінійно поєднувати два вищевказані рішення\(\exp\left(ix\sqrt{\dfrac{2mE_x}{\hbar^2}}\right)\) та\(\exp\left(-ix\sqrt{\dfrac{2mE_x}{\hbar^2}}\right) \) досягти функції, яка зникає при\(x=0\):
\[A(x) = \exp\left(ix\sqrt{\frac{2mE_x}{\hbar^2}}\right) - \exp\left(-ix\sqrt{\frac{2mE_x}{\hbar^2}}\right).\]
Допускається лінійно комбінувати розв'язки рівняння Шредінгера, які мають однакову енергію (тобто вироджені), оскільки рівняння Шредінгера є лінійними диференціальними рівняннями. Аналогічний процес повинен бути застосований для\(B(y)\) досягнення функції, яка зникає при\(y=0\):
\[B(y) = \exp\left(iy\sqrt{\frac{2mE_y}{\hbar^2}}\right) - \exp\left(-iy\sqrt{\frac{2mE_y}{\hbar^2}}\right).\]
Далі вимога\(A(x)\) і\(B(y)\) зникнення, відповідно, при\(x=L_x\) і, відповідно\(y=L_y\), дає рівняння, яким можна підкорятися тільки в тому випадку, якщо\(E_x\) і\(E_y\) приймати конкретні значення:
\[ \exp\left( iL_x \sqrt{\frac{2mE_x}{\hbar^2}} \right)-\exp\left(-iL_x\sqrt{\frac{2mE_x}{\hbar^2}}\right)=0\text{, and}\]
\[ \exp \left( iL_y \sqrt{\frac{2mE_y}{\hbar^2}} \right) - \exp \left(-iL_y\sqrt{\frac{2mE_y}{\hbar^2}} \right) = 0.\]
Ці рівняння еквівалентні (тобто за допомогою\(\exp(ix) = \cos(x) + i \sin(x)\))
\[\sin\left(L_x\sqrt{\frac{2mE_x}{\hbar^2}}\right) = \sin\left(L_y\sqrt{\frac{2mE_y}{\hbar^2}}\right) = 0.\]
Знаючи, що\(\sin(\theta)\) зникає при\(q = n\pi\), бо\(n=1,2,3,\cdots,\) (хоча\(\sin(n\pi)\) функція зникає для\(n=0\), ця функція зникає для всіх\(x\) або\(y\), отже, є неприйнятною, оскільки вона представляє нульову щільність ймовірності у всіх точках простору), можна зробити висновок, що енергій\(E_x\) і\(E_y\) може припускати тільки цінності, які підкоряються:
\[L_x\sqrt{\frac{2mE_x}{\hbar^2}} =n_x\pi,\]
\[L_y\sqrt{\frac{2mE_y}{\hbar^2}} =n_y\pi\]
або
\[E_x = \frac{n_x^2\pi^2 \hbar^2}{2mL_x^2}\]
і
\[E_y = \frac{n_y^2\pi^2 \hbar^2}{2mL_y^2}, \text{ with } n_x \text{ and } n_y =1,2,3, \cdots\]
і
\[E = V_0 +E_x+ E_y.\]
Важливо підкреслити, що саме накладення граничних умов, що виражають той факт, що електрон просторово обмежений, дає початок квантованим енергіям. За відсутності просторового ув'язнення, або з утриманням лише в\(x = 0\) або\(L_x\) або тільки при\(y = 0\) або\(L_y\), квантовані енергії не будуть реалізовані.
У цьому прикладі обмеження електрона до скінченного інтервалу уздовж обох\(y\) координат\(x\) і дає енергії, які квантуються вздовж обох осей. Якщо електрон був обмежений вздовж однієї координати (наприклад, між ними\(0 \le x\le L_x\)), але не вздовж іншої (\(B(y)\)тобто або обмежений зникненням лише в\(y=0\)\(y=L_y\) або в жодній точці), то загальна енергія\(E\) лежить у континуумі; її\(E_x\) складова квантується, але \(E_y\)не є. Аналоги таких випадків виникають, наприклад, для триатомної молекули, що містить одну міцну і одну слабку зв'язок. Якщо зв'язок з вищою енергією дисоціації збуджується до рівня, якого недостатньо, щоб розірвати її, але що перевищує енергію дисоціації слабшого зв'язку, виникає ситуація, яка особливо цікава. При цьому один має два вироджених стану.
- один з міцним зв'язком, що має високу внутрішню енергію і слабкий зв'язок, що має низьку енергію (\(\psi_1\)), і
- секунду з сильним зв'язком, що має мало енергії і слабкий зв'язок, що має більш ніж достатньо енергії, щоб розірвати його (\(\psi_2\)).
Хоча експеримент може підготувати молекулу в стані, який містить тільки колишній компонент (тобто,\(\Psi(t=0)= C_1\psi_1 + C_2\psi_2\) з,\(C_2 = 0\))\(C_1 = 1\), зв'язок між двома виродженими функціями (індукованих термінами в гамільтоніан Н, які були проігноровані при визначенні\(\psi_1\) і\(\psi_2\)) може спричинити \(\Psi = \exp(-itH/\hbar) \Psi(t=0)\)істинна хвильова функція набувати компонент другої функції в міру розвитку часу. У такому випадку говорять про внутрішню коливальну енергетичну релаксацію (IVR), що призводить до одномолекулярного розкладання молекули.
Енергії та хвильові функції для зв'язаних станів
Для дискретних енергетичних рівнів енергії задані функції, які залежать від квантових чисел, по одній для кожного ступеня свободи, яка квантується
Повертаючись до ситуації, в якій рух обмежено по обох осях, результуючі сумарні енергії і хвильові функції (отримані шляхом вставки квантових енергетичних рівнів в вирази для\(A(x)\) і\(B(y)\)) виглядають наступним чином:
\[E_x = \frac{n_x^2\pi^2 \hbar^2}{2mL_x^2}\]
і
\[E_y = \frac{n_y^2\pi^2 \hbar^2}{2mL_y^2}\]
\[E = E_x + E_y +V_0\]
\[\psi(x,y) = \sqrt{\frac{1}{2L_x}}\sqrt{\frac{1}{2L_y}}\left[\exp\bigg(\frac{in_x\pi x}{L_x}\bigg) -\exp\bigg(-\frac{in_x\pi x}{L_x}\bigg)\right]\left[\exp\bigg(\frac{in_y\pi y}{L_y}\bigg) -\exp\bigg(-\frac{in_y\pi y}{L_y}\bigg)\right] \]
з\(n_x\) і\(n_y =1,2,3, \cdots\).
Два\(\sqrt{\dfrac{1}{2L}}\) фактори включені, щоб гарантувати, що\(y\) нормалізується:
\[\int |\psi(x,y)|^2 dx,dy = 1.\]
Нормалізація\(|\psi(x,y)|^2\) дозволяє правильно ідентифікувати як щільність ймовірності знаходження електрона в точці\(x\),\(y\).
На малюнку 1. 13 наведено графіки чотирьох таких двовимірних хвильових функцій для\(n_x\) і\(n_y\) значень (1,1), (2,1), (1.2) та (2,2) відповідно.
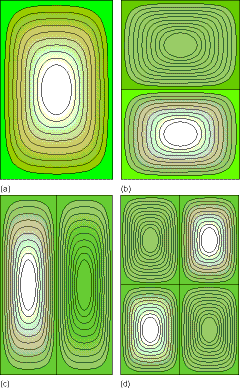
Зверніть увагу, що функції зникають на межах коробки, і зверніть увагу, як кількість вузлів (тобто нулів, що зустрічаються, коли хвильова функція коливається від позитивного до негативного) пов'язана з\(n_y\) квантовими числами та енергією.\(n_x\) Ця модель більшої кількості вузлів, що означають вищу енергію, - це та, з якою ми стикаємося знову і знову в квантовій механіці, і це те, що студент повинен мати можливість використовувати, щоб вгадати відносні енергії хвильових функцій, коли їх ділянки знаходяться під рукою. Нарешті, ви також повинні помітити, що, як і в одновимірному випадку коробки, будь-яка спроба класично інтерпретувати ймовірності,\(P(x,y)\) відповідні вищезазначеним квантовим хвильовим функціям, призведе до невдачі. Як і в одновимірному випадку, класичний\(P(x,y)\) буде постійним уздовж зрізів фіксованих\(x\) і змінних\(y\) або зрізів фіксованих\(y\) і варіюючих\(x\) всередині коробки, оскільки швидкість там постійна. Однак квантові\(P(x,y)\) графіки, принаймні для малих квантових чисел, не є постійними. Для великих\(P(x,y)\) і ny значень квантові\(P(x,y)\) графіки знову, за принципом квантово-класичної відповідності, наближаються до (постійної) класичної\(P(x,y)\) форми, крім класичних поворотних точок (тобто біля країв двовимірної коробки).
Якщо замість того, щоб обмежуватися прямокутним загоном, електрон був обмежений лежати в колі радіуса R, рівняння Шредінгера більш сприятливо виражається в полярних координатах\((r, \theta)\). Перетворення частинних похідних, що з'являються у рівнянні Шредінгера
\[- \dfrac{\hbar^2}{2m} (\frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2})\psi(x,y) +V(x,y) \psi(x,y) = E\psi(x,y)\]
в полярні координати і розуміючи, що потенціал залежить від\(r\), але не від\(\theta\) дає
\[ - \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r}) +\frac{1}{r^2} \frac{\partial^2}{\partial \theta^2}) \psi(r, \theta) + V (r) \psi(r, \theta) = E\psi(r, \theta).\]
Знову використовуючи поділ змінних для заміни
\[\psi(r, \theta) = A(r) B(\theta)\]
в рівняння Шредінгера і діливши на\(AB\), отримаємо
\[- \frac{1}{A} \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})A(r)) +V_0 – \frac{1}{B} \dfrac{\hbar^2}{2m} (\frac{1}{r^2}\frac{\partial^2 B(\theta)}{\partial \theta^2}) = E\]
де\(V_0\) - значення потенціалу всередині кругової області. Перші два терміни зліва та праворуч не містять посилання\(E\) на\(\theta\), тому кількість\(\dfrac{1}{B} \dfrac{\partial^2 B(\theta)}{\partial \theta^2}\) повинна бути незалежною від\(\theta\):
\[\frac{1}{B} \frac{\partial^2 B(\theta)}{\partial \theta^2} = c\]
Більш того, оскільки координати\((r, \theta +2\pi)\) описують\((r, \theta)\) і одну і ту ж точку в просторі,\(B(\theta)\) повинні підкорятися
\[B(\theta) = B(\theta +2 \pi).\]
Розв'язки вищевказаного диференціального рівняння для\(B(\theta)\) умови періодичності
\[B(\theta) = \frac{1}{\sqrt{2\pi}} \exp(± in \theta); n = 0, 1, 2, ….\]
Це означає, що рівняння для радіальної частини хвильової функції
\[- \frac{1}{A} \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})A(r)) +V_0 – \frac{1}{B}\dfrac{\hbar^2}{2m} (\frac{1}{r^2}n^2) = E\]
або
\[r^2 \frac{d^2A}{dr^2} + r \frac{dA}{dr} –n^2 A +\frac{2mr^2}{\hbar^2} (E-V_0)A = 0 .\]
Це диференціальне рівняння, ймовірно, вам не знайоме, але виявляється, це рівняння підкоряється так званим функціям Бесселя. Функції Бесселя, позначені\(J_n(ax)\) підкорятися
\[x^2 \frac{d^2J}{dx^2} +x \frac{dJ}{dx} – n^2 J + a^2 x^2 J = 0\]
Отже, наша\(A\) функція
\[A(r) = J_n\left(\sqrt{\frac{2m(E-V_0)}{\hbar^2}}r\right).\]
Тоді функції повної хвилі
\[\psi(r, \theta) = A(r) B(\theta) = N J_n\left(\sqrt{\frac{2m(E-V_0)}{\hbar^2}}r\right) \frac{1}{\sqrt{2\pi}} \exp(± in \theta)\]
де\(N\) - константа нормалізації. Власні значення енергії\(E_{j,n}\) не можуть бути виражені аналітично, як у системі частинок в коробці (де ми використовували знання нулів функції гріха для визначення\(E_n\)). Однак, знаючи, що\(A(r)\) має зникнути\(R = R\), ми можемо використовувати таблиці (наприклад, див. Kreyszig, E. Розширена інженерна математика, 8-е видання; John Wiley and Sons, Inc.: Нью-Йорк, 1999), які дають значення,\(x\) при яких\(J_n(x)\) зникає, щоб визначити набір власних значень, пов'язаних з кожне значення квантового числа моменту моменту\(n\). У наведеній нижче таблиці ми перерахуємо перші п'ять значень при яких\(J_0\)\(J_1\), і\(J_2\) зникають.
Значення,\(x\) при яких\(J_n(x)\) зникають для\(n = 0, 1\), і\(2\)
Якщо називати значення, при яких\(J_{n(x)}\) зникає\(z_{n,j}\), то енергії даються як
\[E_{n,j} = V_0 + \dfrac{(z_{n,j})^2 \hbar^2}{2mR^2}.\]
З упорядкування\(z_{n,j}\) значень, показаних в таблиці вище, ми бачимо, що впорядкування енергетичних рівнів буде\(z_{0.1}\)\(z_{1,1}\)\( z_{1,2}\)\(z_{1,0}\),\(z_{1,1}\),\(z_{1,2}\),,,, і так далі, незалежно від розміру кола\(R\) або маси частинки\(m\).
Стан з\(n = -1\) має ту ж енергію, що і з\(n = 1\); так само\(n = -2\) має ту ж енергію, що і\(n=2\). Отже, всі, крім\(n = 0\) станів, подвійно вироджені; єдина відмінність між такими парами станів - це відчуття термінів моменту моменту моменту моменту\(\exp(\pm ni \theta)\). Ці енергетичні рівні залежать як від квантового числа моменту моменту\(n\), так і від радіального квантового числа,\(j\) і вони\(R\) залежать від того, як енергії частинок в коробці залежать від довжини коробки\(L\). На малюнку 1.13а ми показуємо графіки щільностей ймовірності\(|\psi(r,\theta)|^2\) для\(n = 0, 1\),\(2\) і для\(j = 1, 3\), а також проілюструємо, як кількість радіальних вузлів\(j\) збільшується зі збільшенням.\(5\)

Характер\(|\psi(r,\theta)|^2\) також змінюється с\(n\). Для\(n = 0\), існує висока амплітуда для частинки, що знаходиться в центрі кола, але для\(n > 0\), немає амплітуди в центрі. Це аналогічно тому, що можна знайти для атомних орбіталів;\(s\) орбіталі мають ненульову амплітуду в ядрі, але p, d і вищі орбіталі цього не роблять.
Розберемо ще кілька легких проблем, які в якійсь мірі можна вирішити аналітично. Це допоможе проілюструвати, як граничні умови породжують квантування і як кількість квантових чисел залежить від розмірності задачі. При розгляді частинки маси, що\(m\) рухається в трьох вимірах, але обмежена залишатися в межах сфери радіуса R, ми замінюємо три декартові координати\(x, y,\) і\(z\) сферичними координатами\(r\)\(\theta\), і\(\phi\). Роблячи це, змінює терміни кінетичної енергії рівняння Шредінгера на те, що ми показуємо нижче
\[-\frac{\hbar^2}{2mr^2}\left(\frac{\partial}{\partial r}\left(r^2\frac{\partial\psi}{\partial r}\right)\right) -\frac{\hbar^2}{2m} \frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2m}\frac{1}{r^2\sin\theta}\frac{\partial^2 \psi}{\partial\phi^2}+ V(r)\psi = E\psi.\]
Беручи потенціал бути\(V_0\) (константа) для\(0 \le r \le R\), і нескінченний для\(r > R\), ми можемо знову використовувати поділ змінних для прогресу у вирішенні цього тривимірного диференціального рівняння. підставляємо
\[\psi(r,\theta,\phi) = Y_{L,M} (\theta,\phi) F(r)\]
у рівняння Шредінгера та беручи до уваги, що так звані сферичні гармонійні функції\(Y_{L,M} (\theta,\phi)\) підкоряються наступним:
\[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial Y_{L,M}}{\partial\theta}\right)+ \frac{1}{\sin^2\theta}\frac{\partial^2 Y_{L,M}}{\partial\phi^2}= - L(L+1) Y_{L,M}.\]
Це зводить рівняння Шредінгера до рівняння для радіальної функції\(F(r)\):
\[-\frac{\hbar^2}{2mr^2}\left(\frac{\partial}{\partial r}\left(r^2\frac{\partial F}{\partial r}\right)\right) + \frac{\hbar^2}{2mr^2}L(L+1)F + V_0 F = EF.\]
Знову ж таки, це рівняння, ймовірно, вам не знайоме, але його можна переробити таким чином, що робить його еквівалентним рівнянню, підкоряється так званим сферичним функціям Бесселя.
\[ x^2\frac{d^2j_L(x)}{dx^2} +2x \frac{dj_L(x)}{dx} +[x^2 –L(L+1)] j_L(x) = 0\]
шляхом прийняття
\[x = \sqrt{\frac{2m(E-V_0)}{\hbar^2}} r.\]
Результатом є те, що хвильові функції для цієї задачі зводяться до
\[\psi(r,\theta,\phi) = N Y_{L,M} (\theta,\phi) j_L\bigg(\sqrt{\frac{2m(E-V_0)}{\hbar^2}} r\bigg)\]
де\(N\) - константа нормалізації. Енергії визначаються вимагаючи\(\psi(r,\theta,\phi)\)
зникнути при\(r = R\), що аналогічно наполяганню на тому, що сферична функція Бесселя зникає\(r = R\) в попередній задачі, яку ми вивчали. Значення,\(x (z_{L,n})\) при яких\(j_L(x)\) зникають знову, можна знайти в різних таблицях, включаючи наведені раніше. Деякі з цих значень наведені нижче для ілюстрації.
Значення,\(x\) при яких\(j_L(x)\) зникають для\(L = 0, 1, 2, 3\), і\(4\)
|
н=1 |
н=2 |
н=3 |
п=4 |
|
|---|---|---|---|---|
|
L=0 |
3.142 |
6.283 |
9.425 |
12.566 |
|
L=1 |
4.493 |
7,725 |
10.904 |
14.066 |
|
Л = 2 |
5.763 |
9.095 |
12.323 |
15.515 |
|
L=3 |
6.988 |
10.417 |
13 698 |
16.924 |
|
L=4 |
8.183 |
11.705 |
15.040 |
18.301 |
З значень\(z_{L,n}\), людина знаходить енергії з
\[E_{L,n} = V_0 + \frac{(z_{L,n})^2\hbar^2}{2mR^2}.\]
Знову ж таки, ми бачимо, як енергія залежить від розмірів стримуючої області (характеризується\(R\)) дуже сильно так само, як і в більш ранніх системах. Ми також бачимо, що\(E\) залежить від квантового числа моменту моменту\(L\) (так само, як це було в попередньому прикладі) і від маси частинки. Однак енергетичне впорядкування цих рівнів відрізняється від того, що ми бачили раніше, як відображено в упорядкуванні\(z_{L,n}\) значень, показаних у наведеній вище таблиці. Енергії з'являються в порядку (\(L=0\)\(n=1\);;\(L=-2\)\(n=1\);\(L=2\)\(n=1\);\(L=0\)\(n=2\);\(L=3\)\(n=1\);\(L=1\)\(n=2\), і так далі, і це вірно для будь-якого розміру сфери\(R\) і будь-якої маси частинок m.
Якщо замість того, щоб бути обмеженою рухатися в межах сферичного об'єму, частинка обмежена рухатися по поверхні сфери або радіуса\(R\), змінна\(R\) фіксується (at\(R = R\)) і рівняння Шредінгера стає
\[-\frac{\hbar^2}{2m} \frac{1}{R^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2m}\frac{1}{R^2\sin^2\theta}\frac{\partial^2 \psi}{\partial\phi^2}+ V_0\psi = E\psi.\]
Використання
\[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial Y_{L,M}}{\partial\theta}\right)+ \frac{1}{\sin^2\theta}\frac{\partial^2 Y_{L,M}}{\partial\phi^2}= - L(L+1) Y_{L,M}.\]
ми бачимо, що хвильові функції - це сферичні гармоніки, а енергії задаються
\[E_{L,M} = V_0 +\frac{L(L+1)\hbar^2}{2mR^2}\]
Зверніть увагу, що енергії залежать від\(M\) квантового числа,\(L\) але не від нього. Отже, кожен стан, що належить до рівня,\(L\) є\(2L+1\) складчастим виродженим тому, що\(M\) коливається від\(-L\) до\(L\).
Нарешті, якщо замість того, щоб бути обмеженим рухатися в межах кола радіуса R, частинка була обмежена рухатися по поверхні кола, двовимірне рівняння Шредінгера, оброблене раніше, зменшило б до
\[- \frac{\hbar^2}{2mR^2} \frac{\partial^2\psi(\theta)}{\partial q^2} + V_0 \psi(\theta) = E\psi(\theta).\]
Рішення - звичні функції
\[\psi(\theta) = \sqrt{(1/2 \pi)} \exp(in\theta)\]
з\(n = 0, ±1, ±2, …\)
і енергії є
\[E_n = \frac{n^2 \hbar^2}{2mR^2} + V_0.\]
Зверніть увагу, що квантування енергії виникає тому, що кутовий імпульс квантується бути\(nh\); ця умова виникла, в свою чергу, умовою, що
\[\psi(\theta) = \psi(q +2\pi).\]
Як і у випадку частинки, що рухається в межах кругової області, стани з подвійно\(n > 0\) вироджуються; різниця між парами таких станів відображає відчуття їх кутового моменту.
Ці модельні проблеми будуть розглядатися в розділі 2 як дуже корисні уявлення про ситуації, що виникають, коли електрон обмежений всередині або на поверхні різних наноскопічних частинок. Наразі вони обговорювалися, щоб проілюструвати, як поділ змінних іноді може бути використаний для розкладання рівняння Шредінгера на одновимірні звичайні диференціальні рівняння та показати, як це граничні умови (або\(y\) обмежують зникнення на певних відстанях, або наполягаючи на тому, що \(y\)бути періодичними, коли це доречно), які виробляють квантування. Важливо зазначити, що саме тоді, коли частинка просторово обмежена (наприклад, коли її хвильова функція була змушена зникнути в двох місцях\(x = 0\) і\(x = L_x\)), що квантовані рівні енергії призводять. Коли частинка не так просторово захоплена, її енергія не буде квантована. Ви побачите таку поведінку знову і знову, коли ми досліджуємо інші моделі електронних, коливальних та обертальних рухів у молекулах.
Квантована дія також може бути використана для отримання енергетичних рівнів
Існує інший підхід, який можна використовувати для пошуку енергетичних рівнів і особливо простий у використанні для систем, рівняння Шредінгера яких роздільні. Так звана класична дія (позначається\(S\)) частинки, що рухається з імпульсом p уздовж шляху, що веде від початкової координати в початковий\(q_i\) час\(t_i\) до кінцевої координати\(q_f\) часу,\(t_f\) визначається:
\[S = \int_{\textbf{q}_i;t_i}^{\textbf{q}_f;t_f}\textbf{p}\cdot\textbf{dq} .\]
Тут вектор імпульсу p містить моменти по всіх координатах системи, а вектор координат\(q\) аналогічно містить координати по всіх таких ступенях свободи. Наприклад, у розглянутій вище двовимірній задачі частинки в коробці\(\textbf{q} = (x, y)\) має дві складові\(\textbf{p} = (p_x, p_y)\), а інтеграл дії:
\[ S =\int_{x_i;y_i;t_i}^{x_f;y_f;t_f}(p_xdx+p_ydy).\]
При обчисленні таких дій важливо пам'ятати про знак імпульсу, коли частка рухається від початкових до кінцевих позицій. Приклади, наведені нижче, допоможуть прояснити ці питання і покажуть, як застосувати ідею.
Для систем, для яких гамільтоніан роздільний, інтеграл дії розкладається на суму таких інтегралів, по одному для кожного ступеня свободи. У двовимірному прикладі адитивність Н:
\[ H = H_x + H_y = \frac{p_x^2}{2m} + \frac{p_y^2}{2m} + V(x) + V(y)\]
\[ = - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + V(x) - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial y^2} + V(y)\]
означає, що\(p_x\) і\(p_y\) може бути вирішено самостійно з точки зору потенціалів,\(V(x)\) а\(V(y)\) також енергій\(E_x\) і\(E_y\) пов'язаних з кожним окремим ступенем свободи:
\[p_x = \pm\sqrt{2m(E_x-V(x))}\]
\[p_y = \pm\sqrt{2m(E_y-V(y))} ;\]
знаки на\(p_x\) і\(p_y\) повинні бути обрані, щоб належним чином відображати рух, який частка насправді переживає в будь-який момент часу. Підстановка цих виразів у інтеграл дії дає:
\[ S = S_x + S_y\]
\[= \int_{x_i;t_i}^{x_f;t_f} \pm\sqrt{2m(E_x-V(x))} dx + \int_{y_i;t_i}^{y_f;t_f} \pm\sqrt{2m(E_y-V(y))} dy.\]
Показано, що зв'язок між цими класичними інтегралами дії та існуванням квантованих енергетичних рівнів передбачає прирівнювання класичної дії до руху, що є періодичним між лівою та правою точкою повороту, як для класичної частинки, що піддається періодичному коливальному руху, до наступного кратна константі Планка:
\[S_{\text{closed}} = \int_{q_i;t_i}^{q_f;t_f} qdq= (n +\frac{1}{2}) h,\]
де індекс квантування\(n\) коливається від 0 до\(\infty\) з кроком одиниці. Крім того, для руху в замкнутому кутовому шляху, як для частинки, що рухається по круговому або еліптичному шляху, умова квантування дії говорить:
\[S_{\text{closed}} =\int_{q_i;t_i}^{q_f;t_f} pdq = nh,\]
де знову\(n\) коливається від 0 до\(\infty\) з кроком одиниці.
Коли дія-квантування, як описано вище, застосовується до так званої задачі гармонічного осцилятора (це служить найпростішою розумною моделлю вібрації двоатомної молекули AB), яку ми вивчимо пізніше в квантовій формі, виражається загальна енергія як сума кінетичної та потенційної енергій.
\[E = \frac{p^2}{2m} + \frac{k}{2} x^2\]
де\[m = \dfrac{m_Am_B}{m_A + m_B}\] - відновлена маса двоатомної молекули AB,\(k\) є силовою константою, що описує зв'язок між А і В,\(x\) є зміщенням довжини зв'язку, а p - імпульс, пов'язаний з довжиною зв'язку. Вимога квантованої дії потім читає
\[(n +\frac{1}{2}) h = \int p dx = \int \sqrt{2\mu(E-k/2 x^2)} dx.\]
Цей інтеграл здійснюється між\(\sqrt{2E/k}\) лівою\(x = - \sqrt{2E/k}\) і правою поворотними точками коливального руху і назад знову утворюють замкнутий шлях. Проведення цього інтеграла і прирівнювання його до\((n +\frac{1}{2}) h\) дає наступний вираз для енергії\(E\):
\[E = (n +\frac{1}{2}) (\hbar^2\pi) \sqrt{\dfrac{k}{\mu}} .\]
Якщо квантовому\(n\) числу дозволяється приймати цілі значення від 1\(n = 0\), 2 до нескінченності, ці енергетичні рівні узгоджуються з результатами повної квантової обробки, які ми отримаємо пізніше.
Для прикладу застосування такого підходу до задачі, пов'язаної з рухом по замкнутому контуру, розглянемо вільне (тобто без потенціалу, що впливає на її кутовий рух) обертання двоатомної молекули AB, що має фіксовану довжину зв'язку R. Енергію обертання можна записати як
\[E=\frac{p_\phi^2}{2\mu R^2}\]
де - імпульс, пов'язаний з обертанням і\(m\) - зменшена маса молекули АВ. Розв'язування та вставлення цього в рівняння дії-квантування, придатне для руху вздовж замкнутого циклу, дає
\[\int_{\phi=0}^{\phi=2\pi} p_\phi d\phi=\int_{\phi=0}^{\phi=2\pi} \sqrt{2\mu R^2E} d\phi = \sqrt{2\mu R^2 E}(2\pi) = nh.\]
Рішення для енергії\(E\) потім дає
\[E=\frac{(nh)^2}{(2\pi)^22\mu R^2}=\frac{n^2h^2}{2\mu R^2},\]
який є точно таким же результатом, як ми отримали раніше при розв'язанні рівняння Шредінгера для руху частинки, що рухається по колу.
Тепер застосуємо квантування дій до кожної з незалежних координат двовимірної частинки в коробковій задачі. Дві окремі умови квантування дії читають:
\[\big(n_x +\dfrac{1}{2}\big) h =\int_{x=0}^{x=L_x} \sqrt{2m(E_x-V(x))} dx +\int_{x=L_x}^{x=0} -\sqrt{2m(E_x-V(x))} dx \]
\[ (n_y +\dfrac{1}{2}) h = \int_{y=0}^{y=L_y} \sqrt{2m(E_y-V(y))} dy +\int_{y=L_y}^{y=0} -\sqrt{2m(E_y-V(y))} dy .\]
Зверніть увагу, що знак моментів є позитивним у кожному з перших інтегралів, що з'являються вище (тому що частинка рухається від\(x = 0\) до\(x = L_x\), і аналогічно для\(y\) -motion, і, таким чином, має позитивний імпульс) і негативним у кожному з других інтегралів (тому що рух від \(x = L_x\)до\(x = 0\) (і аналогічно для\(y\) -motion) і, таким чином, частка має негативний імпульс). У межах області, обмеженої\(0 \le x\le L_x; 0 \le y\le L_y\), потенціал є постійним і може бути прийнятий як нуль (це якраз дає нашу точку відліку для загальної енергії). Використовуючи цей факт, і повертаючи верхню і нижню межі, і, таким чином, знак, у другому інтегралах вище, виходить:
\[\big(n_x +\dfrac{1}{2}\big) h = 2\int_{x=0}^{x=L_x} \sqrt{2mE_x} dx= 2\sqrt{2mE_x} L_x\]
\[\big(n_y +\dfrac{1}{2}\big) h = 2\int_{y=0}^{y=L_y} \sqrt{2mE_y} dy= 2\sqrt{2mE_y} L_y.\]
Вирішуючи для\(E_x\) і\(E_y\), можна знайти:
\[E_x =\frac{[\big(n_x +\dfrac{1}{2}\big)h]^2}{8mL_x^2}\]
\[E_y =\frac{[\big(n_y +\dfrac{1}{2}\big)h]^2}{8mL_y^2} .\]
Це не ті самі квантовані рівні енергії, які виникли, коли граничні умови хвильової функції були узгоджені при\(x = 0\),\(x = L_x\) і\(y = 0\),\(y = L_y\). У підході до рівняння Шредінгера енергетичні вирази не мали\(\dfrac{1}{2}\) коефіцієнта +, який з'являється у вищевказаному результаті на основі дії. Виявляється, що для потенціалів, які визначаються кусково, оскільки потенціал частинки в коробці є (тобто потенціал зазнає нескінченного стрибка при\(x = 0\) і\(x = L\)), умова квантування дії повинна бути змінена. Приклад того, як і чому потрібно зробити цю модифікацію, наведено в статті групи професора Білла Міллера (JE Adams and WH. Miller, J. Chem. Фіз. 67, 5775-5778 (1977)), але я не буду обговорювати це далі тут, оскільки його деталі виходять за рівень цього тексту. Досить сказати, що для періодичного руху між двома поворотними точками на плавному (тобто некусковому) потенціалі,\((n+\dfrac{1}{2})h\) є правильним значенням квантування дії. Для кутового руху по замкнутому контуру nh є належним значенням. Але для періодичного руху між поворотними точками на кусковому потенціалі модифікації, розглянуті у вищезгаданому посиланні, повинні бути застосовані, щоб викликати квантування дій для відтворення правильного квантового результату.
Використання квантування дій, як показано вище, стало дуже важливим інструментом. Це дозволило вченим досягти великого прогресу в напрямку подолання розриву між класичними та квантовими описами молекулярної динаміки. Зокрема, використовуючи класичні поняття, такі як траєкторії, а потім нав'язуючи умови квантованої дії, люди змогли розробити так звані напівкласичні моделі молекулярної динаміки. У таких моделям можна зберегти багато класичного розуміння, будуючи квантові ефекти, такі як квантування енергії, енергії нульової точки та перешкоди. Як на моєму веб-сайті Theory Page, так і з статей, доступних на веб-сайті професора Вільяма Міллера, одного з піонерів напівкласичної теорії, застосованої до хімії, ви можете дізнатися більше про цю тему.
Перш ніж покинути цей розділ, варто трохи докладніше обговорити квантування енергії і моменту моменту моменту, яке відбувається при лікуванні вільного одновимірного обертального руху частинки по колу або лінійної жорсткої молекули, обмеженої лежати на площині. Коли ми використовували квантування дій для вирішення такої проблеми, ми отримали квантовані енергії
\[E=\frac{n^2h^2}{2\mu R^2}\]
який, через енергетичний вираз, заданий в терміні кутового моменту
\[E=\frac{p_\phi^2}{2\mu R^2},\]
означає, що сам кутовий імпульс квантується
\[p_\phi=\pm nh.\]
Це той самий результат, який ми отримуємо, коли шукаємо власні функції та власні значення квантової механіки оператора\(\textbf{L}_z\) кутового імпульсу. Як ми показали раніше, цей оператор, при обчисленні як\(z\) -компонент\(\textbf{R} \times \textbf{p}\), може бути записаний в полярних\((r, \theta, \phi)\) координатах як
\[L_z = - i \hbar \dfrac{d}{d\phi}.\]
Власні функції цього оператора мають вигляд\(\exp(ia\phi)\), а власні значення - a h Оскільки геометрії з азимутальними кутами, рівними\(\phi\) або рівними,\(\phi + 2\pi\) є точно такими ж геометріями, функція\(\exp(ia\phi)\) повинна бути точно такою ж, як\(\exp(ia(\phi+2\pi))\). Це може бути тільки в тому випадку, якщо a є цілим числом. Таким чином, робиться висновок, що тільки інтегральні кратні h можуть бути допущені значення\(z\) -складової моменту моменту.
Експериментально вимірюють\(z\) -складову моменту моменту, поміщаючи систему, що володіє кутовим імпульсом, в магнітне поле напруженості B і спостерігаючи, скільки\(z\) -компонентних енергетичних станів виникає. Це розщеплення на енергетичних рівнях називається ефектом Зеемана. Наприклад, атом бору з одним непарним електроном його\(2\pi\) орбітальна має одну одиницю орбітального кутового моменту, тому знаходять три окремі\(z\) -складові значення, які зазвичай позначаються\(m = -1, m=0,\) і\(m=1\). Інший приклад пропонує атом скандію з одним непарним електроном в орбіталі d; стану цього атома розщеплюються на п'ять (\(m = -2, -1, 0, 1, 2\))\(z\) -складових станів. У кожному випадку знаходять\(2L + 1\) значення\(m\) квантового числа, а оскільки L є цілим числом,\(2L + 1\) є непарним цілим числом. Обидва ці спостереження узгоджуються з очікуванням того, що для\(L_z\) власних значень можуть виникати лише цілі значення, отримані в результаті квантування дії та з граничної умови\(\exp(ia\phi) = \exp(ia(\phi+2\pi))\).
Однак було помічено, що деякі види не мають 3, 5 або 7 або 9\(z\) -компонентних станів, а парну кількість таких станів. Зокрема, спостерігається, що електрони, протони або нейтрони мають лише\(z\) двокомпонентні власні значення. Це також спостерігається, наприклад, у атомі бору, згаданому вище, якщо досліджувати подальші розщеплення рівнів\(2\pi\) (m = -1, 0 та 1), спричинених дією магнітного поля на спін непарного електрона. Оскільки, як ми обговорюємо пізніше в цьому тексті, всі кутові моменти мають\(z\) -компонентні власні значення, які відокремлені один від одного одиничними кратними h, один змушений зробити висновок, що ці три основні частинки будівельного блоку (електрони, протони та нейтрони) мають\(z\) -компонент власні значення\(\dfrac{1}{2} \hbar\) і\(-\dfrac{1}{2} \hbar\). Поява напівінтегральних кутових моментів не узгоджується з результатом дії-квантування або спостереженням, зробленим раніше, що\(\phi\) і\(\phi + 2\pi\) відповідають точно тій же фізичній точці в координатному просторі, що, в свою чергу, передбачає, що можливі тільки повноцілі кутові моменти.
Роздільна здатність вищевказаного парадоксу (тобто як можуть існувати напівцілі кутові моменти?) передбачає усвідомлення того, що деякі кутові моментивідповідають не\(\textbf{R} \times \textbf{p}\) кутовим моментам фізичної маси, що обертається, а, натомість, є внутрішніми властивостями певних частинок. Тобто внутрішні кутові моменти електронів, протонів і нейтронів не можна розглядати як виникають при обертанні деякої маси, яка містить ці частинки. Натомість такі внутрішні кутові моменти є фундаментальними вбудованими в характеристики цих частинок. Наприклад, два\(\dfrac{1}{2} \hbar\) та\(-\dfrac{1}{2} \hbar\) кутові стану імпульсу електрона, зазвичай позначаються a і b, відповідно, є двома внутрішніми станами електрона, які вироджуються за відсутності магнітного поля, але які представляють два різних стану електрона. Аналогічно протон має\(\dfrac{1}{2} \hbar\) і\(-\dfrac{1}{2} \hbar\) стану, як і нейтрони. Всі такі напівінтегральні стани моменту моменту не можуть бути враховані за допомогою класичної механіки, але, як відомо, виникають у квантовій механіці. Це означає, що, коли ми навчаємо вступну хімію молодим студентам, некоректно говорити, що спін-стани електрона вгору і вниз (a і b) можна розглядати з точки зору маси електрона, що обертається за годинниковою стрілкою або проти годинникової стрілки навколо якоїсь осі. Такі кутові моменти спінінг-маси можуть мати лише ціле значення; напівціле кутове момента не може і не повинно бути описано терміном обертових мас.
Дія також може бути використана для генерації хвильових функцій
Інтеграли дії, обчислені за класичними описами руху на потенційних енергетичних поверхнях, також можуть бути використані для генерації наближених квантових хвильових функцій. Таким чином, це пропонує ще один шлях для встановлення зв'язку між класичним і квантовим світами. Щоб побачити, як такий зв'язок може виникнути безпосередньо з рівняння Шредінгера, почнемо з незалежного від часу рівняння Шредінгера для однієї частинки маси, що\(m\) рухається на потенціалі\(V(r)\), який залежить від координат положення частинки\(r\):
\[E\Psi(r)=-\frac{\hbar^2}{2m}\nabla^2\Psi(r)+V(r)\Psi(r).\]
Потім ми виражаємо комплексну хвильову функцію як постійну дійсну амплітуду A, помножену на складну фазу, яку ми записуємо як:
\[\Psi(r)=A\exp(iW(r)/\hbar).\]
Підставляючи цей вираз до рівняння Шредінгера, дається рівняння для\(W\):
\[E=V+\frac{(\nabla W)^2}{2m}-i\hbar\frac{\nabla^2W}{2m}.\]
Це рівняння містить як дійсну, так і уявну складові (н.б.,\(W\) саме по собі є складним). Зазвичай це вирішується, припускаючи, що\(W(r)\) може бути розширена в ряді потужності в змінній\(\hbar\). Це розширення мотивується тим, що якщо\(\dfrac{\nabla^2 W}{2m}i\hbar\) коефіцієнт у вищевказаному рівнянні знехтувати, отримане рівняння
\[0=V-E+\frac{(\nabla W)^2}{2m}\]
мав би сенс,\(\nabla W(r)\) якби дорівнювали класичному імпульсу частинки. Отже, беручи\(\hbar\rightarrow 0\) межу рівняння для,\(W(r)\) здається, зводить це рівняння квантової механіки до класичного результату, в якому\(\nabla W(r) = p(r)\).
Отже, підставляючи
\[W(r)=W_0(r)+hW_1(r)+\hbar^2W_2(r)+\cdots\]
у вищевказане рівняння для\(W(r)\) і збирання разом усіх членів заданої потужності в виробляє рівняння для різних\(W_n(r)\), перші два з яких читають:
\[0=2m(V-E)+(\nabla W_0)^2\]
і
\[0=2\nabla W_0\cdot \nabla W_1-i\nabla^2 W_0.\]
Щоб спростити подальше обговорення цієї так званої напівкласичної теорії хвильових функцій, обмежимо увагу випадком, в якому існує лише одна просторова координата. Для дво- або тривимірних випадків\(\nabla W_0\) і\(\nabla W_1\) є векторними величинами, і рішення цих рівнянь значно складніше, особливо якщо потенціал не\(V(\textbf{r})\) можна розділити на адитивні внески від кожної зі змінних. Коли є тільки одна просторова координата, і є скалярні величини.
Перше рівняння може бути розв'язане для\(W_0(r)\) і дає два незалежних рішення (тобто відповідні знаку ±):
\[W_0(r)=\pm\int\sqrt{2m(E-V(r^\prime))dr^\prime},\]
кожен з яких буде реальним коли\(E > V(r)\) (тобто в класично дозволених регіонах простору) і уявним коли\(E < V(r)\) (тобто в класично заборонених регіонах). Зверніть увагу, що\(W_0(r)\) містить ціле число, рівне класичному імпульсу\(p(r)=\sqrt{2m(E-V(r)) }\).
Рівняння для також\(W_1(r)\) може бути вирішено:
\[W_1(r)=\frac{i}{2}\ln[\sqrt{2m(E-V(r))}].\]
Отже, через перший порядок в\(\hbar\), напівкласичні хвильові функції
\[\Psi(r)=A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\exp\left(\frac{i\hbar}{2h}i\ln[\sqrt{2m(E-V(r))}]\right).\]
\[=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\]
Ці пари хвильових функцій часто виражаються як
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\]
в регіонах космосу\(E > V\), де, і
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right)\]
в класично заборонених регіонах де\(V > E\). Зверніть увагу, що хвильові функції в класично дозволених областях мають густини ймовірності, задані
\[\Psi^*\Psi=\frac{A^2}{\sqrt{2m(E-V(r))}}\]
яка є саме класичною щільністю ймовірності, про яку ми говорили раніше в цій главі. Імовірність обернено пропорційна швидкості частинки в місці r, і має ту ж сингулярність, що і класична ймовірність в поворотних точках (де\(V = E\)). Навпаки, щільність ймовірності в регіонах, де ростуть\(V > E\) або розпадаються експоненціально в межах цих класично заборонених регіонів.
Давайте подивимося, як ці напівкласичні хвильові функції можуть бути застосовані до деяких модельних задач, про які ми говорили раніше. Для одновимірної проблеми частинки в коробці дві експоненціально зростаючі та розкладаються функції не потрібні\(R > L\), оскільки в регіонах\(R < 0\) і хвильова функція може бути прийнята зникає. У межах області\(0 \le r \le L\) існують дві незалежні хвильові функції
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right),\]
і потенціал\(V(r’)\) постійний (назвемо потенціал в цьому регіоні\(V_0\)). Отже, інтеграція, що з'являється в цих двох хвильових функціях, може бути здійснена, щоб дати
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right).\]
Ми можемо об'єднати ці дві функції, щоб генерувати функцію, яка зникне\(R = 0\) (як це повинно бути для цієї проблеми частинки в коробці):
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\left[\exp\left(\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right)-\exp\left(-\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right)\right].\]
Потім ми можемо використовувати умову, яка також\(\Psi\) повинна зникнути,\(R = L\) щоб отримати рівняння,\(E\) яке визначає дозволені енергії:
\[0=\left[\exp\left(\frac{iL}{\hbar}\sqrt{2m(E-V_0)}\right)-\exp\left(-\frac{iL}{\hbar}\sqrt{2m(E-V_0)}\right)\right]=2i\sin\left(\frac{L}{\hbar}\sqrt{2m(E-V_0)}\right),\]
що означає, що
\[E=V_0+\frac{n^2\pi^2\hbar^2}{2mL^2}.\]
Ці енергії точно такі ж, як ми виявили, коли ми розв'язували рівняння Шредінгера для цієї модельної задачі.
Інформативно зазначити, що ці напівкласичні хвильові функції, які не є точними, оскільки вони були отримані шляхом збереження лише термінів до першої потужності\(\hbar\), змогли генерувати квантові вузлові візерунки (тобто перешкоди) та квантовані енергетичні рівні, хоча вони містили класичні такі поняття, як імпульс на різних позиціях у просторі. Саме шляхом накладення двох функцій, що мають однакову енергію, були отримані вузлові візерунки.
Давайте тепер розглянемо, що відбувається, коли ми застосуємо напівкласичну хвильову функцію до задачі гармонійного осцилятора, яку також обговорювали раніше. При цьому є два класичних поворотних точки\(r_1\) і\(r_2\) при яких\(E = V(r)\). Напівакласичні хвильові функції, відповідні трьом регіонам (дві класично заборонені та одна класично дозволена):
\[\Psi_1=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A_1\exp\left(-\frac{1}{\hbar}\int_{r_2}^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right),r\ge r_2.\]
\[\Psi_2=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A_2\exp\left(\frac{1}{\hbar}\int_{r_1}^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right),r\le r_1.\]
\[\Psi_3=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}\left[A_3\exp\left(\frac{i}{\hbar}\int_{r_1}^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)-A_{3^\prime}\exp\left(-\frac{i}{\hbar}\int_{r}^{r_2}\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\right],r_1\le r\le r_2.\]
Перші два розпадаються експоненціально в межах двох класично заборонених регіонів. Третя - це комбінація двох незалежних розв'язків в межах класично дозволеної області, з амплітудами двох розв'язків, визначеними коефіцієнтами\(A_3\) і\(A_{3’}\). Амплітуди\(A_1\) і\(A_2\) множення хвильових функцій у двох класично заборонених областях, і всі чотири амплітуди, а також енергія\(E\) повинні бути визначені шляхом (i) нормалізації загальної хвильової функції, щоб підкорятися
\[\int_{-\infty}^{\infty}\Psi^*\Psi dr=1\]
і (2) шляхом узгодження хвильових функцій\(\Psi_1\)\(\Psi_3\) і їх перших похідних при\(R = r_1\), і хвильових функцій\(\Psi_2\)\(\Psi_3\) і їх перших похідних в\(R = r_2\).
Перш ніж розглядати, як це узгодження хвильової функції може бути досягнуто, дозвольте мені відзначити цікаву властивість фактора, що входить в експоненціальну напівкласичної хвильової функції. Спочатку використовуємо два вирази
\[\frac{dW_0}{dr}=\pm\sqrt{2m(E-V(r))} \]
і
\[\frac{dW_1}{dr}=\dfrac{i\dfrac{d\sqrt{2m(E-V)}}{dr}}{2\sqrt{2m(E-V)}}\]
наведено вище для перших двох компонентів,\(W(r)\) а потім використовувати гармонійну форму\(V(r)\)
\[V(r)=\frac{1}{2}kr^2.\]
Далі оцінюємо інтеграл\(\dfrac{dW}{dr}\) для замкнутого класичного шляху, по якому система рухається від лівої поворотної точки
\[r_1=-\sqrt{\frac{2E}{k}}\]
до правого поворотного моменту
\[r_2=\sqrt{\frac{2E}{k}}\]
і знову повертаємося до лівого поворотного пункту. Внесок інтеграції\(\dfrac{dW_0}{dr}\) вздовж цього замкнутого шляху є (наприклад, знак + використовується для першої частини шляху, оскільки частинка має позитивний імпульс, а знак — застосовується до зворотної частини шляху, коли частинка має негативний імпульс):
\[W_0=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr\]
який є саме інтегралом дії, який ми розглядали раніше в цій главі, коли ми обчислювали для класичного гармонійного осцилятора. Внесок від інтеграції\(\dfrac{dW_1}{dr}\) по цьому замкнутому шляху можна оцінити шляхом першого написання
\[\frac{dW_1}{dr}=\dfrac{i\dfrac{d\sqrt{2m(E-1/2 kr^2)}}{dr}}{2\sqrt{2m(E-1/2 kr^2)}}=\frac{-ikr}{4(E-1/2 kr^2)}.\]
Інтеграл від\(r_1\) до\(r_2\) цієї величини може бути здійснений (використовуючи підстановку\(r = \sqrt{2E/k} y\)) як
\[\dfrac{-ik}{4}\int_{-\sqrt{2E/k}}^{\sqrt{2E/k}}\dfrac{rdr}{(E-1/2kr^2)}=\dfrac{-ik}{4}\int_{-1}^{1}\dfrac{\dfrac{2E}{k}ydy}{E(1-y^2)}=\dfrac{-i}{4}\int_{-1}^{1}\dfrac{ydy}{(1-y)(1+y)}.\]
Оцінка інтегралу, що залишився на правій стороні, може бути здійснена за допомогою контурної інтеграції (студенти бакалаврату, можливо, не стикалися з цим предметом в теорії складних змінних; я відношу їх до pp. 367-377 Методи теоретичної фізики, P.M. Morse і H. Feshabach, Макгроу-Хілл, Нью-Йорк (1953) або p. 113 Прикладні комплексні змінні, Дж. Деттман, Макміллан Ко. Нью-Йорк (1965). Основне рівняння з контурної інтеграції говорить про те\(\int \dfrac{f(z)}{(z-a)}dz\), що інтеграл форми, де\(z = a\) є сингулярність, дорівнює\(2\pi if(a)\). Наш інтеграл має особливості в\(y = 1\) і в\(y = -1\), так що є два таких внески. Чистий результат полягає в тому, що наш інтеграл зводиться до
\[\frac{-i}{4}\int_{-1}^{1}\frac{ydy}{(1-y)(1+y)}=\frac{i}{4}2\pi i\left[\frac{1}{2}+\frac{-1}{-2}\right]=-\frac{\pi}{2}.\]
Отже, внесок в інтеграл,\(\dfrac{dW_1}{dr}\) що виникає з\(r_1\) до\(r_2\) дорівнює\(–\pi/2\). Інтеграл від\(r_2\) спини до\(r_1\) дає інший фактор або\(–\dfrac{\pi}{2}\). Поєднання інтеграла\(\dfrac{dW_0}{dr}\) та інтеграла\(\dfrac{dW_1}{dr}\) (помноженого на тому, що\(W = W_0 + \hbar W_1 + …\)) дає наступний кінцевий результат
\[W=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\pi \hbar\]
Якщо початкове квантування Бора застосовується до інтегралу\(\dfrac{dW}{dr}\) уздовж замкнутого класичного шляху:
\[W=nh,n=1,2,3,\cdots\]
наш результат вище говорить, що
\[nh=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\frac{1}{2}h\]
який такий же, як
\[\int p(r)dr=\big(n+\dfrac{1}{2}\big)h.\]
Це означає, що\(\dfrac{1}{2}\) фактор, що виникає в умові квантування дії для періодичних рухів між двома поворотними точками, може розглядатися як виникає внаслідок першої квантової корекції (тобто терміна першого порядку в\(\hbar\)) до напівкласичної хвильової функції. Нагадаємо, що прирівнювання цього класичного інтеграла дії до\(\big(n+\dfrac{1}{2}\big) h\) дало правильні (тобто квантові) енергії для цієї задачі гармонічного осцилятора.
Ми бачили, як можна визначити напівкласичну хвильову функцію, яка її просторова щільність ймовірності, як вона може будувати перешкоди (для досягнення належних вузлових моделей), і як квантування її дії може дати правильні дозволені рівні енергії. Однак є одне питання, яке ми не повністю вирішували. Для розв'язання коефіцієнтів,\((A_1, … A_{3’})\) що множать напівкласичні хвильові функції в класично дозволених і заборонених областях, хвильові функції\(\Psi_1\)\(\Psi_3\) та їх перші похідні повинні бути узгоджені на\(r = r_1\), а хвильові функції\(\Psi_2\)\(\Psi_3\) та їх перші похідні повинні збігатися при\(R\) =\(r_2\). На жаль, деталі цього процесу узгодження досить складні і вимагають більш докладного вивчення природи хвильових функцій поблизу класичних поворотних точок\(\Psi_1\), де кожен з\(\Psi_2\), і\(\Psi_3\) містять фактори виду\(\sqrt{\sqrt{2m(-E+V(r)}}\) в своїх знаменниках. Повинно бути зрозуміло, що відповідні функції та їх похідні, що містять такі особливості, створюють особливі проблеми. Я не буду йти далі в цю справу тут; скоріше, я посилаю зацікавленого читача на стор. 268-279 Квантової механіки, 3-е видання, Л.І. Шифф, Макгроу-Хілл, Нью-Йорк (1968) для гарного лікування цього так званого WKB підходу до питання відповідності.
