1.3: Наближення народженого Оппенгеймера

Одне з найважливіших наближень, що стосуються застосування квантової механіки до молекул та молекулярних іонів, відомий як наближення Борна-Оппенгеймера (BO). Основна ідея цього наближення передбачає усвідомлення того, що в повних електронів-плюс-ядрах гамільтонових операторів, введений вище.

\[H = \sum_i \left[- \dfrac{\hbar^2}{2m_e} \dfrac{\partial^2}{\partial q_i^2} \right]+ \dfrac{1}{2} \sum_{j\ne i} \dfrac{e^2}{r_{i,j}} - \sum_{a,i} \dfrac{​Z_ae^2}{r_{i,a}} + \sum_a \left[- \dfrac{\hbar^2}{2m_a} \dfrac{\partial^2}{\partial q_a^2}\right]+ \dfrac{1}{2} \sum_{b\ne a} \dfrac{​Z_aZ_b e^2}{r_{a,b}} \]

часові шкали, з якими рухаються електрони і ядра, зазвичай досить різні. Зокрема, важкі ядра (тобто навіть H ядро важить майже в 2000 разів більше, ніж важить електрон) рухаються (тобто вібрують і обертаються) повільніше, ніж легші електрони. Наприклад, типові коливальні рухи зв'язку відбуваються з часовими шкалами ок.\(10^{-14}\) с, молекулярні обертання вимагають\(10^{-100}\) разів більше часу, але електрони зазнають періодичних рухів в межах своїх орбіт на часовій шкалі\(10^{-17}\) s, якщо вони проживають в межах ядра або валентних орбіталів. Таким чином, ми очікуємо, що електрони зможуть оперативно «підлаштовувати» свої рухи під набагато повільніше рухаються ядра.

Це спостереження мотивує розглядати рішення рівняння Шредінгера для руху електронів в присутності нерухомих ядер як спосіб представлення повністю скоригованого стану електронів при будь-яких фіксованих положеннях ядер. Звичайно, тоді ми повинні мати спосіб описати відмінності між тим, як поводяться електрони та ядра за відсутності цього наближення та тим, як вони рухаються в межах наближення. Ці відмінності породжують так звані ненароджені корекції оппенгеймера, безрадіаційні переходи, поверхневі хмелі та неадіабатичні переходи, з якими ми розберемося пізніше.

Слід зазначити, що таке поділ часових шкал між швидкими електронними і повільними вібраційними і обертовими рухами не стосується, наприклад, станів Рідберга атомів і молекул. Як обговорювалося раніше, в таких станах електрон в орбіталі Рідберга має набагато меншу швидкість і набагато більшу радіальну протяжність, ніж для типових ядра або валентних орбіталей. З цієї причини виправлення моделі БО, як правило, важливіші при роботі з державами Рідберга.

Електронний гамільтоніан, який стосується рухів електронів у присутності затиснутих ядер

\[H = \sum_i \left[- \dfrac{\hbar^2}{2m_e} \dfrac{\partial^2}{\partial q_i^2} \right]+ \dfrac{1}{2} \sum_{j\ne i} \dfrac{e^2}{r_{i,j}} - \sum_{a,i} \dfrac{​Z_ae^2}{r_{i,a}} \dfrac{1}{2} \sum_{b\ne a} \dfrac{​Z_a Z_b e^2}{r_{a,b}}\]

виробляє як власні значення через рівняння

\[H \psi_J(q_j|q_a) = E_J (q_a) \psi_J(q_j|q_a)\]

енергії\(E_K (q_a)\), які залежать від того, де знаходяться ядра (тобто координати {\(q_a\)}). Як власні функції, людина отримує так звані електронні хвильові функції {\(\psi_K(q_i|q_a)\)}, які також залежать від того, де знаходяться ядра. Енергії\(E_K(q_a)\) - це те, що ми зазвичай називаємо потенційними енергетичними поверхнями. Приклад такої поверхні показаний на малюнку 1.5.

Малюнок 1.5. Двовимірна потенційна енергетична поверхня показує локальні мінімуми, перехідні стани та шляхи, що їх з'єднують.

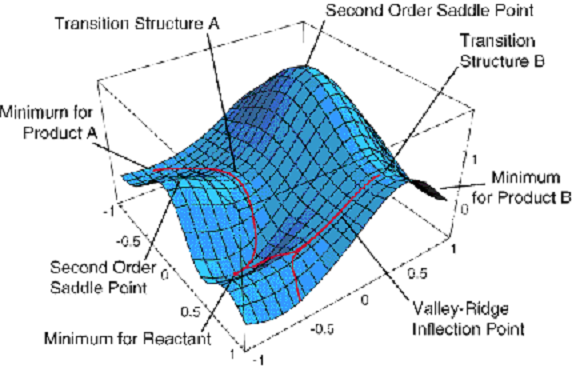
Ця поверхня залежить від двох геометричних координат\(\{q_a\}\) і є ділянкою одного конкретного власного значення\(E_J(q_a)\) проти цих двох координат.

Хоча цей сюжет має більше інформації про нього, ніж ми зараз обговоримо, варто відзначити кілька особливостей. Здається, є три мінімуми (тобто точки, де похідна відносно обох координат\(E_J\) зникає і де поверхня має позитивну кривизну). Ці точки відповідають, як ми побачимо ближче до кінця цього вступного матеріалу, геометрії стабільних молекулярних структур. Поверхня також відображає дві точки сідла першого порядку (позначені перехідними структурами A і B), які з'єднують три мінімуми. Ці точки мають нульову першу\(E_J\) похідну відносно обох координат, але мають один напрямок негативної кривизни. Як ми покажемо пізніше, ці пункти описують перехідні стани, які відіграють вирішальну роль у кінетиці переходів між трьома стабільними геометріями.

Майте на увазі, що на малюнку 1.5 показана лише одна з\(E_J\) поверхонь; кожна молекула має поверхню наземного стану (тобто ту, яка є найнижчою за енергією), а також нескінченну кількість збуджених поверхонь. Давайте тепер повернемося до нашого обговорення моделі БО і запитаємо, що робити, коли в руках така енергетична поверхня.

Рух ядер згодом, у моделі BO, вважається, що підкоряється рівнянню Шредінгера, в якому

\[\displaystyle\sum_a [- \dfrac{\hbar^2}{2m_a} \dfrac{\partial^2}{\partial q_a^2} ]+ \dfrac{1}{2} \sum_{b\ne a} \dfrac{Z_aZ_be^2}{r_{a,b}} + E_K(q_a)\]

визначає ротаційно-вібраційний гамільтоніан для конкретного\(E_K\) енергетичного стану, що цікавить. Обертальна та коливальна енергії та хвильові функції, що належать кожному електронному стану (тобто для кожного значення індексу\(K\) в\(E_K(q_a)\)), потім знаходять шляхом розв'язання\(E_K\) гамільтоніана.

Ця модель BO становить основу більшої частини того, як хіміки розглядають молекулярну структуру та молекулярну спектроскопію. Наприклад, що стосується формальдегіду\(H_2C=O\), ми говоримо про електронний стан синглетного заземлення (при цьому всі електрони спінові парні і займають найнижчі орбіталі енергії) та його коливальні та обертальні стани, а також\(\pi\rightarrow \pi^*\) електронні\(n\rightarrow \pi^*\) стани та їх коливальні та обертальні. рівні. Хоча набагато більше буде сказано про ці поняття пізніше в цьому тексті, студент повинен усвідомлювати поняття електронних енергетичних поверхонь (тобто {\(E_K(q_a)\)}) і станів вібрації-обертання, які належать кожній такій поверхні.

Слід зазначити, що\(3N\) декартові координати {\(q_a\)}, використовувані для опису позицій\(N\) ядер молекули, можуть бути замінені на 3 декартові координати, що\((X,Y,Z)\) вказують центр маси\(N\) ядер та\(3N-3\) інші так звані внутрішні координати, які може використовуватися для опису орієнтації молекули (ці координати з'являються в обертальної кінетичній енергії) та її довжин зв'язків та кутів (ці координати з'являються у коливальній кінетичній та потенційній енергіях). Коли замість\(3N\) декартових координат використовуються центр маси та внутрішні координати, енергетичні поверхні Борна-Оппенгеймера {\(E_K(q_a)\)} залежать лише від внутрішніх координат. Більше того, якщо енергія молекули не залежить від її орієнтації (наприклад, якщо вона вільно рухається в газовій фазі), то {\(E_K(q_a)\)} також буде залежати не від 3 орієнтаційних координат, а лише від\(3N-6\) коливальних координат.

Ознайомившись з поняттями операторів, хвильових функцій, гамільтоніана і його рівняння Шредінгера, важливо зараз розглянути кілька прикладів застосування цих понять. Розглянуті нижче приклади були обрані, щоб надати читачеві цінний досвід у вирішенні рівняння Шредінгера; вони також були обрані тому, що вони утворюють найбільш елементарні хімічні моделі електронних рухів в кон'югованих молекулах і в атомах, обертання лінійних молекул і коливання хімічні зв'язки.

Ваше перше застосування квантової механіки - рух частинки в одному вимірі

Це дуже важлива проблема, рішення якої хіміки використовують для моделювання найрізноманітніших явищ.

Почнемо з вивчення руху однієї частинки маси\(m\) в одному напрямку, яке ми будемо називати,\(x\) перебуваючи під впливом позначеного потенціалу\(V(x)\). Класичним виразом для сумарної енергії такої системи є\(E = \dfrac{p^2}{2m} + V(x)\), де\(p\) - імпульс частки по осі х. Щоб зосередитися на конкретних прикладах, розглянемо, як ця частинка рухалася б, якби\(V(x)\) були форми, показані на рис. 1. 6, де загальна енергія\(E\) позначається положенням горизонтальної лінії.

Малюнок 1. 6. Три характерних потенціалу, що показують ліву і праву класичні поворотні точки при енергіях, позначених горизонтальними лініями.

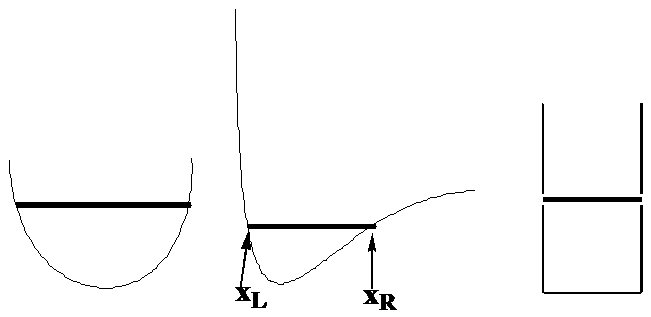
Класична щільність ймовірності

Я хотів би, щоб ви уявили, якою буде щільність ймовірності для цієї частинки, що рухається із загальною енергією\(E\) та з\(V(x)\) різною, як ілюструють наведені вище три графіки. Щоб концептуалізувати щільність ймовірності, уявіть, що частинка має миготливу лампу, прикріплену до неї, і подумайте, що ця лампа блимає, скажімо 100 разів за кожен раз, коли частинка повинна завершити повний транзит від лівої поворотної точки, до правої точки повороту і назад до першого. Поворотні точки\(x_L\) і\(x_R\) є положеннями, при яких частка, якби вона рухалася за законами Ньютона, змінила б напрямок (як імпульс змінюється знак) і оберталася. Ці позиції можна знайти, запитавши, де імпульс йде до нуля:

\[0 = p = \sqrt{2m(E-V(x)}.\]

Це положення, де вся енергія з'являється як потенційна енергія\(E = V(x)\) і відповідає на вищезазначених малюнках точкам, де темні горизонтальні лінії торкаються\(V(x)\) ділянок, як показано на центральному графіку.

Щільність ймовірності при будь-якому значенні\(x\) представляє частку часу, яку частка витрачає при цьому значенні\(x\) (тобто всередині\(x\) і\(x+dx\)). Подумайте про формування цієї щільності, дозволяючи миготливій лампі, прикріпленій до частинки, пролити світло на фотографічну пластину, яка піддається цьому світлу для багатьох коливань частинки між\(x_L\) і\(x_R\). Як варіант, можна висловити ймовірність того\(P(x) dx\), що частка витрачає між\(x\) і\(x + dx\) шляхом ділення просторової відстані\(dx\) на швидкість (р/м) частинки в точці\(x\):

\[P(x)dx = \sqrt{2m(E-V(x))} \;m\; dx.\]

\(E\)Оскільки постійна протягом усього руху частинки,\(P(x)\) буде невеликою при\(x\) значеннях, де частинка швидко рухається (тобто, де\(V\) низька) і буде високою, де частка рухається повільно (де\(V\) висока). Так, фотопластинка покаже яскраву область, де\(V\) висока (тому що частка повільно рухається в таких областях) і менша яскравість, де\(V\) низька. Зверніть увагу, однак, що у міру\(x\) наближення до класичних поворотних точок швидкість наближається до нуля, тому вищевказане вираз for\(P(x)\) буде наближатися до нескінченності. Це не означає, що ймовірність знаходження частинки в поворотній точці нескінченна; це означає, що щільність ймовірності там нескінченна. Ця дивергенція\(P(x)\) є характеристикою класичної щільності ймовірності, яка буде видно сильно відрізняється від квантової щільності ймовірності.

Суть полягає в тому, що щільності ймовірності, передбачені аналізом класичної ньютонівської динаміки цієї частинки, будуть відображатися як ілюструють графіки гістограми, показані на малюнку 1.7.

Рисунок 1. 7 Класичні графіки ймовірності для трьох показаних потенціалів

Там, де частка має високу кінетичну енергію (і, отже, нижчу\(V(x)\)), вона витрачає менше часу і\(P(x)\) невелика. Там, де частка рухається повільно, вона витрачає більше часу і\(P(x)\) більше. Для ділянки праворуч,\(V(x)\) є постійним всередині «коробки», тому швидкість постійна, отже\(P(x)\), постійна для всіх\(x\) значень всередині цієї одновимірної коробки. Я прошу вас пам'ятати про ці ділянки, тому що вони дуже відрізняються від того, що можна знайти, коли вирішує рівняння Шредінгера для цієї ж проблеми. Також майте на увазі, що ці сюжети представляють те, що можна очікувати, якщо частка рухалася відповідно до класичної ньютонівської динаміки (якої ми знаємо, що це не так!).

Квантове лікування

Для розв'язання квантових механічних хвильових функцій і енергій цієї ж задачі спочатку запишемо гамільтоновий оператор, про який говорилося вище, замінивши\(p\) на\(-i\hbar \dfrac{d}{dx}\):

\[H = -\dfrac{ \hbar^2}{2m} \dfrac{d^2}{dx^2} + V(x).\]

Потім ми намагаємося знайти рішення\(H\psi = E\psi\), які\(\psi(x)\) підкоряються певним умовам. Ці умови пов'язані з тим, що\(|\psi (x)|^2\) передбачається щільність ймовірності знаходження частинки між\(x\) і\(x+dx\). Щоб зробити речі максимально простими, давайте зосередимося на потенціалі коробки,\(V\) показаному в правій частині малюнка 1.7. Цей потенціал, виражений як функція\(x\) є:\(V(x) = \infty\) for\(x< 0\) і for\(x> L\);\(V(x) = 0\) для\(x\) між\(0\) і\(L\).

Той факт,\(V\) що нескінченно для\(x< 0\) і для\(x> L\), і що загальна енергія\(E\) повинна бути кінцевою, говорить про те, що\(\psi\) має зникнути в цих двох областях (\(y = 0\)для\(x< 0\) і для\(x> L\)). Ця умова означає, що частинка не може отримати доступ до областей простору, де потенціал нескінченний. Друга умова, яку ми використовуємо, полягає в тому, що вона\(\psi (x)\) повинна бути безперервною; це означає, що ймовірність того, що частинка знаходиться в\(x\) не може бути розривно пов'язана з ймовірністю того, що вона знаходиться в сусідній точці. Також вірно, що просторова похідна\(\dfrac{d\psi}{dx}\) повинна бути безперервною, за винятком точок, де потенціал\(V(x)\) має нескінченний розрив, як це робиться в прикладі, показаному праворуч на малюнку 1.7. Неперервність\(\dfrac{d\psi}{dx}\) відноситься до безперервності імпульсу (нагадаємо,\(-i \hbar \dfrac{\partial}{\partial x}\) є оператором імпульсу). Коли частинка рухається під, наприклад, одним із двох потенціалів, показаних зліва або посередині малюнка 1.7, потенціал плавно змінюється як обмін кінетичною та потенційною енергією під час періодичного руху. На відміну від цього, при русі під потенціалом праворуч від малюнка 1.7 потенціал зазнає раптової зміни напрямку, коли частинка потрапляє в будь-яку стінку. Отже, навіть класично імпульс частинки зазнає розриву в таких поворотних точках жорсткої стінки. Ці умови безперервності\(\psi\) (та її просторової першої похідної) і які\(\psi\) повинні зникнути в областях простору, де потенціал надзвичайно високий, були постульовані піонерами квантової механіки, щоб прогнози квантової теорії відповідали експериментальним спостереження.

Енергії та хвильові функції

Диференціальне рівняння другого порядку

\[- \dfrac{\hbar^2}{2m} \dfrac{d^2\psi}{dx^2} + V(x)\psi = E\psi\]

має два розв'язки (тому що це рівняння другого порядку) в області між\(x= 0\) і\(x= L\) де\(V(x) = 0\):

\[\psi = \sin(kx)\]

і

\[\psi = \cos(kx),\]

де\(k\) визначається як

\[k=\sqrt{2mE/\hbar^2}.\]

Отже, найбільш загальним рішенням є деяке поєднання цих двох:

\[\psi = A \sin(kx) + B \cos(kx).\]

Ми могли б, альтернативно, використовувати\(\exp(ikx)\) і\(\exp(-ikx)\) як два незалежні рішення (ми робимо це пізніше в розділі 1.4, щоб проілюструвати), тому що\(\sin(kx)\) і\(\cos(kx)\) можуть бути переписані з точки зору\(\exp(ikx)\) і\(\exp(-ikx)\); тобто вони охоплюють точно такий же простір.

Той факт, що\(\psi\) повинен зникнути в\(x= 0\) (n.b.,\(\psi\) зникає\(x< 0\) бо\(V(x)\) є нескінченним там і\(\psi\) є безперервним, тому він повинен зникнути в точці\(x= 0\)) означає, що амплітуда зважування\(\cos(kx)\) терміна повинна зникнути, тому що\(\cos(kx) = 1\) при \(x = 0\). Тобто,

\[B = 0.\]

На амплітуду\(\sin(kx)\) терміну не впливає стан, який\(\psi\) зникає при\(x= 0\), так як\(\sin(kx)\) сам зникає при\(x= 0\). Отже, тепер ми знаємо,\(\psi\) що дійсно має вигляд:

\[\psi(x) = A \sin(kx).\]

Умова, яка\(\psi\) також зникає\(x= L\) (тому що вона зникає для того,\(x < 0\) де\(V(x)\) знову нескінченно) має два можливі наслідки. Або\(A = 0\) або\(k\) повинен бути таким, що\(\sin(kL) = 0\). Опція\(A = 0\) призведе до відповіді\(\psi\), яка зникає при всіх значеннях\(x\) і, отже, ймовірність, що зникає скрізь. Це неприпустимо, оскільки це означало б, що частка ніколи ніде не спостерігається.

Інша можливість полягає в тому, що\(\sin(kL) = 0\). Давайте вивчимо цю відповідь, оскільки вона пропонує перший приклад квантування енергії, з яким ви, ймовірно, стикалися. Як відомо, функція гріха зникає в інтегральних кратних\(p\). Звідси\(kL\) має бути декілька кратних\(\pi\); назвемо ціле число\(n\) і запишемо\(Lk = n\pi\) (використовуючи визначення\(k\)) у вигляді:

\[L\sqrt{\dfrac{2mE}{\hbar^2}} = n\pi.\]

Вирішуючи це рівняння для енергії\(E\), отримаємо:

\[E = \dfrac{n^2 \pi^2 \hbar^2}{2mL^2}\]

Цей результат говорить про те, що єдиними енергетичними значеннями, які здатні дати хвильову функцію\(\psi (x)\), яка буде підкорятися вищезазначеним умовам, є ці конкретні\(E\) значення. Іншими словами, не всі енергетичні цінності допускаються в тому сенсі, що вони можуть виробляти\(\psi\) функції, які є безперервними і зникають в регіонах, де\(V(x)\) нескінченно. Якщо хтось використовує енергію\(E\), яка не є одним із дозволених значень, і замінює\(E\) її на\(\sin(kx)\), результуюча функція не зникне при\(x = L\). Сподіваюся, рішення цієї проблеми нагадає вам про скрипкову струну, про яку ми говорили раніше. Нагадаємо, що струна скрипки, прив'язана до\(x = 0\) і на\(x = L\) породила квантування довжини хвилі так само, як умови, які були\(\psi\) безперервними при\(x = 0\) і\(x = L\) давали квантування енергії.

Підставляючи\(k = n\pi/L\) в\(\psi = A \sin(kx)\) дає

\[\psi (x) = A \sin\Big(\dfrac{np_x}{L}\Big).\]

Значення A можна знайти, пам'ятаючи, що\(|\psi|^2\) передбачається представляти щільність ймовірності знаходження частинки при\(x\). Такі щільності ймовірностей повинні бути нормовані, а це означає, що їх інтеграл над усіма\(x\) значеннями повинен дорівнювати одиниці. Отже, ми можемо знайти А, вимагаючи, що

\[1 = \int |\psi(x)|^2 dx = |A|^2 \int \sin^2\Big(\dfrac{np_x}{L}\Big)​dx\]

де інтеграл коливається від\(x = 0\) до\(x = L\). Пошук інтеграла\(\sin^2(ax)\) і розв'язування наведеного вище рівняння для так званої константи нормалізації\(A\) дає

\(A = \sqrt{\dfrac{2}{L}}\)і так

\[\psi(x) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big).\]

Значення, які\(n\) можуть взяти на себе, є\(n = 1, 2, 3, \cdots\); вибір\(n = 0\) є неприйнятним, оскільки він буде виробляти хвильову функцію\(\psi(x)\), яка взагалі зникає\(x\).

Потім повні x- та t- залежні хвильові функції задаються як

\[\Psi(x,t) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big) \exp\bigg[-\dfrac{it}{\hbar}\dfrac{n^2 \pi^2\hbar^2}{2mL^2}\bigg].\]

Зверніть увагу, що просторова\(|\Psi(x,t)|^2\) щільність ймовірності не залежить від часу і дорівнює\(|\psi(x)|^2\) тому, що складна експоненціальна\(\Psi^*\Psi\) зникає при формуванні. Це означає, що ймовірність знаходження частинки при різних значеннях\(x\) не залежить від часу.

Ще одна річ, яку я хочу, щоб ви помітили, це те, що, на відміну від класичного випадку динаміки, не всі енергетичні значення\(E\) допускаються. У ситуації з динамікою Ньютона\(E\) може бути вказано, а імпульс частинки при будь-якому\(x\) значенні тоді визначався в межах знака. На відміну від цього, в квантовій механіці потрібно визначити, вирішуючи рівняння Шредінгера,\(E\) які допустимі значення. Ці\(E\) значення квантуються, тобто вони зустрічаються тільки для дискретних значень\(n\),\(E = \dfrac{n^2 \pi^2h^2}{2mL^2}\) визначених квантовим числом, масою частки m, і характеристиками потенціалу (\(L\)в даному випадку).

Щільність ймовірності

Давайте тепер розглянемо деякі хвильові функції\(\psi (x)\) і порівняємо щільності ймовірностей\(|\psi (x)|^2\), які вони представляють, з класичними щільностями ймовірності, розглянутими раніше. Функції\(n=1\) і\(n=2\) хвильові показані у верхній частині малюнка 1.8. Відповідні квантові щільності ймовірностей показані під хвильовими функціями у двох форматах (як\(x-y\) графіки та затінені ділянки, які могли б стосуватися способу спостереження за місцем розташування частинки, про який ми говорили раніше).

Малюнок 1. 8. Дві найнижчі хвильові функції та густини ймовірностей

Більш повний набір хвильових функцій (для\(n\) діапазону від 1 до 7) показаний на малюнку 1. 9.

Малюнок 1. 9. Сім найнижчих хвильових функцій і енергій

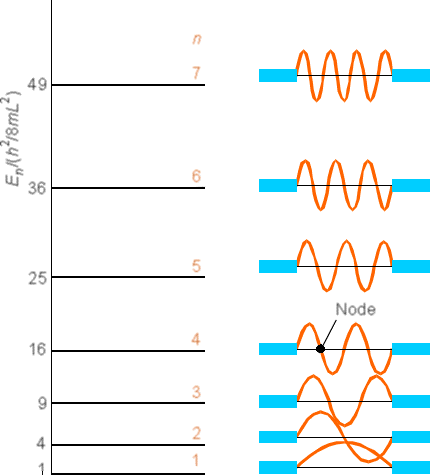
Зверніть увагу, що зі\(n\) збільшенням квантового числа енергія\(E\) також збільшується (квадратично з\(n\) в цьому випадку) і кількість вузлів в\(\psi\) також збільшується. Також зверніть увагу, що щільності ймовірності сильно відрізняються від тієї, з якою ми стикалися раніше для класичного випадку. Наприклад, подивіться на\(n = 2\) щільності\(n = 1\) і порівняйте їх з класичною щільністю, проілюстрованою на малюнку 1.10.

Малюнок 1.10. Класична щільність ймовірності показаного потенціалу

Класичну щільність легко зрозуміти, тому що ми знайомі з класичною динамікою. У цьому випадку ми говоримо, що\(P(x)\) є постійним всередині коробки, оскільки той факт, що\(V(x)\) є постійним, викликає кінетичну енергію і, отже, швидкість частинки залишатися постійною, і це вірно для будь-якої енергії\(E\). На відміну від цього,\(P(x)\) сюжет\(n = 1\) квантової хвильової функції досягає максимуму в середині коробки і падає до нуля біля стін. \(n = 2\)Щільність\(P(x)\) має два піки (один ліворуч від середньої точки коробки, а один праворуч), вузол у середній точці коробки, і падає до нуля біля стін. Одна річ, яку студенти часто запитують мене, це «як частинка отримує від перебування в лівому піку, щоб бути в правій піку, якщо вона має нульовий шанс коли-небудь бути в середній точці, де вузол?» Складність цього питання полягає в тому, що він поставлений в термінології, яка просить класичну відповідь динаміки. Тобто, запитуючи «як частинка отримує...», вимагається відповідь, яка передбачає опис її руху (тобто вона рухається звідси в той час\(t_1\) до туди\(t_2\)). На жаль, квантова механіка не займається такими питаннями, як траєкторія частинки (тобто, де вона знаходиться в різний час), а лише з її ймовірністю десь опинитися (тобто\(|\psi|^2\)). Наступний розділ буде розглядати такі парадоксальні питання ще далі.

Класична та квантова щільності ймовірностей

Як тільки що зазначалося, для більшості початківців студентів квантової механіки спокусливо спробувати інтерпретувати квантову поведінку частинки в класичних умовах. Однак ця пригода сповнена небезпеки і обов'язково зазнає невдачі, оскільки дрібні світлові частинки просто не рухаються за законами Ньютона. Для ілюстрації спробуємо зрозуміти, який вид (класичного) руху був би узгоджений з\(n = 1\) або\(n = 2\) квантовими\(P(x)\) графіками, показаними на малюнку 1. 8. Однак, як я сподіваюся, ви передбачаєте, ця спроба отримати класичне розуміння квантового результату не спрацює в тому, що призведе до безглуздих результатів. Моя точка в тому, щоб змусити вас спробувати таке класичне розуміння, полягає в тому, щоб навчити вас, що класичні та квантові результати просто різні і що ви повинні протистояти прагненню нав'язати класичне розуміння квантовим результатам, принаймні, поки не зрозумієте, за яких обставин класичні та квантові результати. повинен або не повинен бути порівнянним.

Для\(n = 1\) випадку на малюнку 1.8 ми зауважимо, що\(P(x)\) є найвищим у середній точці коробки і зникає при\(x = 0\) і\(x = L\). У класичному світі механіки це означатиме, що частка повільно рухається поблизу\(x = \dfrac{L}{2}\) і швидше поблизу\(x = 0\) і\(x = L\). Оскільки загальна енергія частинки\(E\) повинна залишатися постійною під час руху, в регіонах, де вона рухається повільно, потенціал, який вона відчуває, повинен бути високим, а там, де вона швидко рухається,\(V\) повинен бути малим. Цей аналіз (n.b., заснований на класичних концепціях) призведе нас до висновку, що\(n =1\)\(P(x)\) виникає внаслідок частинки, що рухається в потенціалі, який є високим, близьким\(x = \dfrac{L}{2}\) і низьким, як\(x\) наближається до 0 або L.

Подібний аналіз\(P(x)\) сюжету для\(n = 2\) приведе нас до висновку, що частка, для якої це правильно,\(P(x)\) повинна відчувати потенціал, який є високим посередині між\(x = 0\) і\(x = \dfrac{L}{2}\), високим посередині між і,\(x = \dfrac{L}{2}\) і низьким\(x = L\), близьким\(x = \dfrac{L}{2}\) і близьким. \(x = 0\)і\(x = L\). Ці висновки божевільні, тому що ми знаємо, що потенціал,\(V(x)\) для якого ми розв'язали рівняння Шредінгера, щоб генерувати обидві хвильові функції (і обидві щільності ймовірності) постійний між\(x = 0\) і\(x = L\). Тобто, ми знаємо, що те саме\(V(x)\) стосується частинки, що рухаються в\(n = 1\) і\(n = 2\) станах, тоді як класичний аналіз руху, запропонований вище, свідчить про те, що для цих двох випадків\(V(x)\) відрізняється.

Що не так з нашою спробою зрозуміти квантові\(P(x)\) сюжети? Помилка, яку ми допустили, полягала в спробі застосувати рівняння і поняття класичної динаміки до\(P(x)\) сюжету, який не виник з класичного руху. простіше кажучи, не можна запитати, як рухається частинка (тобто яка її швидкість в різних положеннях), коли частка зазнає квантову динаміку. Більшість студентів, вперше відчуваючи квантові хвильові функції та квантові ймовірності, намагаються думати про частинку, що рухається класичним способом, який узгоджується з квантом\(P(x)\). Ця спроба зберегти ступінь класичного розуміння руху частинки майже завжди зустрічається з розчаруванням, як я проілюстрував на наведеному вище прикладі і проілюструю пізніше в інших випадках.

Продовжуючи цей перший приклад того, як вирішує рівняння Шредінгера і як хтось думає про квантовані\(E\) значення та хвильові функції\(\psi\), дозвольте мені запропонувати трохи більш оптимістичну ноту, ніж запропоновано в попередньому обговоренні. Якщо розглядати\(\psi(x)\) сюжет, показаний на малюнку 1.9 для\(n = 7\), and think of the corresponding \(P(x) = |\psi(x)|^2\), відзначимо, що\(P(x)\) plot would look something like that shown in Figure 1. 11.

Малюнок 1.11. Квантова щільність ймовірності для\(n = 7\) показу семи піків і шести вузлів

Він мав би сім максимумів, розділених шістьма вузлами. Якби ми планували\(|\psi(x)|^2\) для дуже великого\(n\) значення\(n = 55\), наприклад, ми знайшли б\(P(x)\) ділянку, що має 55 максимумів, розділених 54 вузлами, з максимумами, відокремленими приблизно на відстані (1/55L). Такий сюжет при розгляді в грубозернистому сенсі (тобто фокусування з дещо розмитим зором на положеннях і висотах максимумів) дуже нагадує класичний\(P(x)\) сюжет, в якому\(P(x)\) постійний для всіх\(x\). Інший спосіб подивитися на різницю між low-n і high-n квантовими розподілами ймовірностей відображається в так званій локальній довжині хвилі де Броля.

\[\lambda_{\rm local}(x)=\dfrac{h}{\sqrt{2m(E-V(X))}}\]

Можна показати, що класична і квантова ймовірності будуть схожі в областях простору, де

\[\left|\dfrac{d\lambda_{\rm local}}{dx}\right| << 1.\]

Ця нерівність буде вірною, коли\(E\) набагато більше\(V\), ніж, що узгоджується з думкою про те, що високі квантові стани поводяться класично, але воно не буде триматися, коли\(E\) знаходиться лише трохи вище\(V\) (тобто для низькоенергетичних квантових станів і для будь-якого квантового стану поблизу класичного). поворотні точки) або коли\(E\) менше\(V\) (тобто в класично заборонених регіонах).

Підсумовуючи, це загальний результат квантової механіки, що квантові\(P(x)\) розподіли для великих квантових чисел набувають вигляду класичного\(P(x)\) для того ж потенціалу,\(V\) який використовувався для розв'язання рівняння Шредінгера, за винятком близьких поворотних точок і в класично заборонених. регіони. Правда також, що при будь-якій зазначеній енергії класичні та квантові результати узгоджуються краще, коли людина має справу з важкими частинками, ніж для легких частинок. Наприклад, задана енергія\(E\) відповідає більш високому\(n\) квантовому числу у формулі частинки в коробці\(E_n = \dfrac{n^2\hbar^2}{2mL^2}\) для більш важкої частинки, ніж для більш легкої частинки. Значить, більш важкі частинки, рухаючись із заданою енергією\(E\), мають більш класичні розподіли ймовірностей.

Щоб отримати перспективу щодо цього питання, у наведеній нижче таблиці я даю енергетичні рівні\(E_n = \dfrac{n^2\hbar^2}{2mL^2}\) в ккал моль ^-1 для частинки, маса якої становить 1 2000, 20 000 або 200 000 разів маса електрона, обмежена переміщатися в межах одновимірної області довжини\(L\) (в одиницях Бора позначається \(a_0\); 1\(a_0\) = 0,529 Å).

Енергії\(E_n\) (ккал моль ^-1) для різних\(m\) і\(L\) комбінацій

м = 1 м _е

	Л = 1 а 0	Л = 10 а 0	Л = 100 а 0	Л = 1000 а 0
м = 1 м е	3.1 х10 ^3 м ^2	3.1 х10 ^1 п ^2	3.1 х10 ^-1 п ^2	3.1 х10 ^-3 п ^2
м = 2000 м д	1.5 х10 ^0 н ^2	1.5 х10 ^-2 п ^2	1,5 х10 ^-4 п ^2	1,5 х10 ^-6 м ^2
м = 20 000 м д	1,5 х10 ^-1 п ^2	1.5 х10 ^-3 п ^2	1,5 х10 ^-5 н ^2	1,5 х10 ^-7 м ^2
м = 200 000 м е	1.5 х10 ^-2 п ^2	1,5 х10 ^-4 п ^2	1,5 х10 ^-6 м ^2	1,5 х10 ^-8 м ^2

Зрозуміло, що для електронів, навіть коли вільно бродять понад 50-500 нанометрів (наприклад,\(L = 100 a_0\) або\(L = 1000 a_0\)), не потрібно отримувати доступ до дуже високого квантового стану, щоб досягти 1 ккал моль ^-1 енергії (наприклад,\(n= 3\) було б достатньо для\(L =100 a_0\)). Нагадаємо, це високі квантові стани, де очікується, що класичний і квантовий просторовий розподіл ймовірностей буде схожим. Отже, при лікуванні електронів, ймовірно, (майже) завжди доведеться використовувати квантову механіку, і один не зможе покладатися на класичну механіку.

Для світлих ядер, маса яких близько 2000 разів перевищує масу електрона, якщо частка обмежена невеликим діапазоном відстані (наприклад, 1-10\(a_0\)), знову навіть низькі квантові стани матимуть енергію, що перевищує 1 ккал моль ^-1. Тільки коли вільно пересуватися від 100 до 1000\(a_0\), 1 ккал моль ^-1 відповідає відносно великим квантовим числам, для яких очікується майже класична поведінка. Дані, наведені в наведеній вище таблиці, також можуть бути використані для оцінки того, коли можна очікувати квантової поведінки, такої як конденсація Бозе-Ейнштейна. При обмеженні до 100\(a_0\) частинки в діапазоні мас 1 аму мають поступальні енергії в діапазоні\(0.15 n^2\) cal mol ^-1. Розуміючи, що\(RT = 1.98\) cal mol ^{-1 K -1}, це означає, що поступальні температури близько 0,1 К знадобляться, щоб змусити ці частинки зайняти\(n = 1\) свій основний стан.

На відміну від цього, частинки з масами в діапазоні 100 аму, навіть коли вони обмежені

до відстаней приблизно 5 Å, потрібно\(n\) перевищити приблизно 10, перш ніж мати 1 ккал моль ^-1 поступальної енергії. При обмеженні до 50 Å, 1 ккал моль ^-1 вимагає\(n\) перевищити 1000. Отже, важкі частинки навіть при низьких енергіях будуть вести себе класично, за винятком випадків, коли вони обмежені дуже короткими відстанями.

Ми знову зіткнемося з цим так званим квантово-класичним принципом відповідності, коли ми розглянемо інші проблеми моделі. Це важлива властивість розв'язків рівняння Шредінгера, оскільки саме це дозволяє нам подолати розрив між використанням рівняння Шредінгера для обробки дрібних частинок світла та рівняннями Ньютона для макроскопічних (великих, важких) систем.

Час поширення хвильових функцій

Для частинки в коробковій системі, яка існує у власному стані, що\(\psi(x) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big)\) має енергію\(E_n = \dfrac{n^2 \pi^2\hbar^2}{2mL^2}\), хвильова функція, залежна від часу, є

\[\Psi(x,t) = \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{np_x}{L}\Big) \exp\Big(-\dfrac{itE_n}{\hbar}\Big),\]

які можуть бути створені шляхом застосування так званого оператора еволюції часу\(U(t,0)\) до хвильової функції при\(t = 0\):

\[\Psi(x,t) = U(t,0) \Psi(x,0),\]

де явна форма для\(U(t,t’)\) - це:

\[U(t,t’) = \exp\bigg[-\dfrac{i(t-t’)H}{\hbar}\bigg].\]

Функція\(\Psi(x,t)\) має просторову щільність ймовірності, яка не залежить від часу, оскільки

\[\Psi^*(x,t) \Psi(x,t) = \dfrac{2}{L} \sin^2\Big(\dfrac{np_x}{L}\Big) = \Psi^*(x,0) \Psi(x,0)\]

так як\(\exp\Big(-\dfrac{itE_n}{\hbar}\Big) \exp\Big(\dfrac{itE_n}{\hbar}\Big) = 1\). Однак можна готувати системи (навіть у реальних лабораторних умовах) в станах, які не є єдиними власними станами; ми називаємо такі стани суперпозиційними станами. Наприклад, розглянемо частинку, що рухається вздовж осі x в межах коробкового потенціалу, але в стані, хвильова функція якого в якийсь\(t = 0\) початковий час

\[\Psi(x,0) = \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big).\]

Це суперпозиція\(n =1\) і\(n = 2\) власнихстанів. Щільність ймовірності, пов'язана з цією функцією, дорівнює

\[|\Psi(x,0)|^2 = \dfrac{1}{2}\Big\{\dfrac{2}{L} \sin^2\Big(\dfrac{1p_x}{L}\Big)+ \dfrac{2}{L} \sin^2\Big(\dfrac{2p_x}{L}\Big) -2\dfrac{2}{L} \sin\Big(\dfrac{1p_x}{L}\Big)\sin\Big(\dfrac{2p_x}{L}\Big)\Big\}.\]

\(n = 2\)Компоненти\(n = 1\) і, суперпозиція\(\Psi\) і щільність ймовірності при\(t = 0\) показані на перших трьох панелах малюнка 1.12.

Малюнок 1.12. The\(n = 1\) і\(n = 2\) хвильові функції (вгорі ліворуч), їх суперпозиція (вгорі праворуч), а також\(t = 0\) (знизу ліворуч) і еволюціонування часу (знизу праворуч) щільності ймовірності суперпозиції

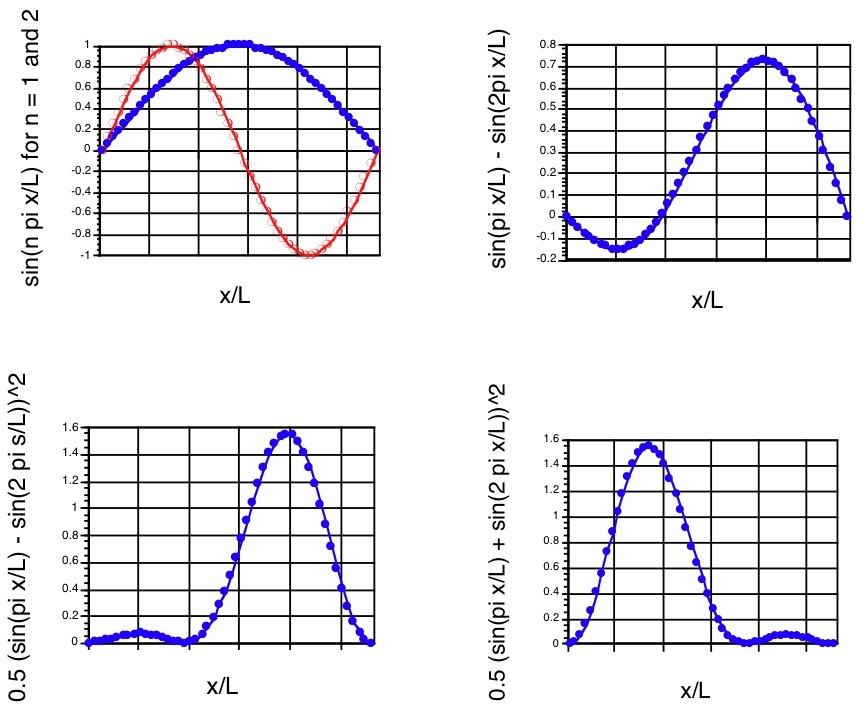
Слід зазначити, що щільність ймовірності, пов'язана з цим станом суперпозиції, не є симетричною щодо\(x=\dfrac{L}{2}\) середньої точки, навіть якщо хвильові функції та щільності\(n = 2\) компонента і є.\(n = 1\) Така щільність описує частинку, локалізовану сильніше в області великого x коробки, ніж в області малого x в\(t = 0\).

Тепер розглянемо хвильову функцію суперпозиції та її щільність в більш пізні часи. Застосування оператора еволюції часу\(\exp\Big(-\dfrac{itH}{\hbar}\Big)\) для\(\Psi(x,0)\) генерації цієї еволюційної функції в часі t:

\[\Psi(x,t) = \exp\Big(-\dfrac{itH}{\hbar}\Big) \left\{\dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big)\right\}\]

\[= {\dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) \exp\Big(-\dfrac{itE_1}{\hbar}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big) \exp\Big(-\dfrac{itE_2}{\hbar}\Big) }.\]

Просторова щільність ймовірності, пов'язана з цим\(\Psi\), становить:

\[|\Psi(x,t)|^2 = \dfrac{1}{2}\Bigg\{\dfrac{2}{L} \sin^2\Big(\dfrac{1p_x}{L}\Big)+ \dfrac{2}{L} \sin^2\Big(\dfrac{2p_x}{L}\Big)-2\dfrac{2}{L} \cos\Big(\dfrac{(E_2-E_1)t}{\hbar}\Big) \sin\Big(\dfrac{1p_x}{L}\Big)\sin\Big(\dfrac{2p_x}{L}\Big)\Bigg\}.\]

При\(t = 0\), ця функція явно зводиться до того, що написано раніше для\(\Psi(x,0)\). Зверніть увагу, що в міру розвитку часу ця щільність змінюється через\(\cos(E_2-E_1)\tau/\hbar\)) фактор, який він містить. Зокрема, зауважте, що при\(t\) переміщенні через певний проміжок часу\(\delta t = \dfrac{\pi\hbar}{E_2-E_1}\) коефіцієнт cos змінює знак. Тобто, для\(t = 0\),\(\cos\) фактор є\(+1\); для\(t = \dfrac{\pi\hbar}{E_2-E_1}\), cos фактор є\(-1\); для\(t = \dfrac{2\pi\hbar}{E_2-E_1}\), він повертається до\(+1\). Результатом цієї зміни часу в коефіцієнті cos є те, що\(|\Psi|^2\) змінюється за формою від тієї, що показана на нижній лівій панелі малюнка 1. 12 до тієї, що показана на нижній правій панелі (at\(t = \dfrac{\pi\hbar}{E_2-E_1}\)), а потім назад до форми в нижній лівій панелі (at\(t = \dfrac{2\pi\hbar}{E_2-E_1}\)). Цю варіацію часу можна інтерпретувати як опис щільності ймовірності частинки (а не її класичного положення!) , Спочатку локалізується в правій частині коробки, рухаючись вліво, а потім назад праворуч. Звичайно, цього разу еволюція буде тривати все більше і більше циклів, оскільки час еволюціонує далі.

Цей приклад ще раз ілюструє труднощі зі спробою локалізації частинок, які описуються квантовими хвильовими функціями. Наприклад, частка, яка характеризується власнимстаном, частіше\(\sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big)\) виявляється поблизу,\(x = \dfrac{L}{2}\) ніж поблизу\(x = 0\) або\(x = L\) через те, що квадрат цієї функції великий поблизу\(x = \dfrac{L}{2}\). Частинку в стані\(\sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big)\), швидше за все, можна знайти поблизу\(x = \dfrac{L}{4}\) і\(x = \dfrac{3L}{4}\), але не поруч\(x = 0\)\(x = \dfrac{L}{2}\), або\(x =L\). Питання про те, як частка в останньому стані рухається від близькості\(x = \dfrac{L}{4}\) до, не\(x = \dfrac{3L}{4}\) є чимось, чим займається квантова механіка. Квантова механіка не дозволяє нам слідувати траєкторії частинки - це те, що нам потрібно знати, коли ми запитуємо, як вона рухається з одного місця в інше. Проте, хвильові функції суперпозиції можуть запропонувати, в деякій мірі, можливість стежити за рухом частинки.

Наприклад, стан суперпозиції написано вище як

\(\dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{1p_x}{L}\Big) – \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{2}{L}} \sin\Big(\dfrac{2p_x}{L}\Big)\)має амплітуду ймовірності, яка змінюється з часом, як показано на малюнку 1.12. Більше того, основний пік цієї амплітуди рухається з боку в бік всередині коробки з часом еволюціонує. Отже, в даному випадку можна сказати, з якою частотою основний пік рухається вперед і назад. У певному сенсі це дозволяє нам стежити за рухами частинки, але лише в тій мірі, в якій ми задоволені приписуванням її розташування до положення головного піку в її розподілі ймовірностей. Тобто ми не можемо насправді стежити за його точним місцем розташування, але ми можемо стежити за місцем, де його дуже ймовірно знайти. Однак зауважте, що час, необхідний частинці для переміщення\(t = \dfrac{\pi\hbar}{E_2-E_1}\) справа наліво, залежить від різниці енергії між двома станами, що сприяють стану суперпозиції, а не від енергії будь-якого з цих станів, що дуже відрізняється від того, що очікувалося б, якби частка рухалася. класично.

Це важливе спостереження, яке я сподіваюся, що студент буде мати на увазі свіжі. Вони також є важливими інгредієнтами сучасної квантової динаміки, в якій локалізовані хвильові пакети, подібні до накладених власних станів, розглянутих вище, використовуються для деталізації положення та швидкості основного піку щільності частинки.

Наведений вище приклад ілюструє, як один час еволюціонує хвильова функція, яка виражається у вигляді лінійної комбінації (тобто суперпозиції) власних станів задачі під рукою. Існує велика кількість поточних зусиль у спільноті теоретичної хімії, спрямованих на розробку ефективних наближень до оператора\(\exp\Big(-\dfrac{itH}{\hbar}\Big)\) еволюції, які не вимагають\(\Psi(x,0)\) явно записати як суму власних станів. Це важливо, тому що для більшості систем, що мають пряме відношення до молекул, не можна вирішити для власних станів; це просто занадто важко зробити. Ви можете знайти значно більш детальну обробку дослідження рівня лікування цього предмета на моєму веб-сайті Theory Page та моєму підручнику QMIC. Однак давайте витратимо трохи часу на короткий вступ до того, що йде мова.

Проблема полягає в тому\(\exp\Big(-\dfrac{itH}{\hbar}\Big) \Psi(q_j)\), щоб висловити, де\(\Psi(q_j)\) є деяка початкова хвильова функція, але не власний стан, таким чином, що не вимагає, щоб спочатку знайти власні стани {\(\psi_J\)}\(H\) і розширити з\(\Psi\) точки зору цих власних станів:

\[\Psi (t=0) = \sum_J C_J \psi_J\]

після чого потрібна функція записується як

\[\exp\Big(-\dfrac{itH}{\hbar}\Big) \Psi(q_j) = \sum_J C_J \psi_J \exp\Big(-\dfrac{itE_J}{\hbar}\Big).\]

Основна ідея полягає в тому, щоб\(H\) розбити оператора на його кінетичні\(T\) та потенційні\(V\) енергетичні складові і усвідомити, що диференціальні оператори з'являються\(T\) тільки в. Важливість цього спостереження полягає в тому, що\(T\) і\(V\) не їздити на роботу, що означає, що не\(TV\) дорівнює\(VT\) (n.b., нагадаємо, що для двох величин коммутіровать означає, що їх порядок появи не має значення). Чому вони не їздять на роботу? Оскільки\(T\) містить другі похідні щодо координат {q_j}, які\(V\) залежать від, тому, наприклад, не\(\dfrac{d^2}{dq^2}(V(q) \Psi(q))\) дорівнює\(V(q)\dfrac{d^2}{dq^2}\Psi(q)\). Той факт, що\(T\) і\(V\) не їздити на роботу є важливим, тому що найбільш очевидною спробою наближення\(\exp\Big(-\dfrac{itH}{\hbar}\Big)\) є написання цієї єдиної експоненціальної з точки зору\(\exp\Big(-\dfrac{itT}{\hbar}\Big)\) і\(\exp\Big(-\dfrac{itV}{\hbar}\Big)\). Однак ідентичність

\[\exp\Big(-\dfrac{itH}{\hbar}\Big) = \exp\Big(-\dfrac{itV}{\hbar}\Big) \exp\Big(-\dfrac{itT}{\hbar}\Big)\]

не є повністю дійсним, як можна бачити, розширюючи всі три вищевказані експоненціальні фактори,\(\exp(x) = 1 + x + \dfrac{x^2}{2!} + \cdots,\) а також зазначивши, що дві сторони вищевказаного рівняння погоджуються лише в тому випадку, якщо можна припустити\(TV = VT\), що, як ми зазначали, не відповідає дійсності.

У більшості сучасних підходів до поширення часу один ділить часовий проміжок\(t\) на безліч (тобто\(P\) з них) невеликих часових зрізів\(\tau = t/P\). Потім висловлює оператор еволюції як добуток\(P\) короткочасних пропагаторів (студент повинен бути знайомий з тим\(H\), що\(T\), і\(V\) є операторами, так що, відтепер я більше не буду обов'язково використовувати жирні літери для цих величин):

\[\exp\Big(-\dfrac{itH}{\hbar}\Big) = \exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \cdots = \left[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \right]^P.\]

Якщо потім можна розробити ефективний засіб розмноження протягом короткого часу\(\tau\), то можна робити це знову і знову\(P\) раз, щоб досягти бажаного повного розмноження.

Показано, що експоненціальний оператор за участю\(H\) може бути краще апроксимований за термінами експоненціального\(T\) та\(V\) експоненціального операторів наступним чином:

\[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \approx \exp\Big(-\dfrac{\tau^2 (TV-VT)}{\hbar^2}\Big) \exp\Big(-\dfrac{i\tau V}{\hbar}\Big) \exp\Big(-\dfrac{i\tau T}{\hbar}\Big).\]

Отже, якщо хтось може бути задоволений поширенням протягом дуже коротких часових інтервалів (щоб цим\(\tau^2\) терміном можна було знехтувати), можна дійсно використовувати

\[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \approx \exp\Big(-\dfrac{i\tau V}{\hbar}\Big) \exp\Big(-\dfrac{i\tau T}{\hbar}\Big)\]

як наближення для пропагатора\(U(t,0)\). Також можна показати, що так зване розщеплене короткочасне вираз

\[\exp\Big(-\dfrac{i\tau H}{\hbar}\Big) \approx \exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big) \exp\Big(-\dfrac{i\tau T}{\hbar}\Big) \exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big) \]

забезпечує ще більш точне представлення короткочасного пропагандиста (оскільки розширення лівої та правої сторони погоджуються на більш високі порядки в\(\tau/\hbar\)).

Щоб прогресувати далі, потім висловлюється, що\(\exp\Big(-\dfrac{i\tau T}{\hbar}\Big)\) діє з\(\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big) \Psi(q)\) точки зору власних функцій оператора кінетичної енергії\(T\). Зверніть увагу, що ці власні функції не залежать від характеру потенціалу V, тому цей крок справедливий для будь-яких і всіх потенціалів. Своїми функціями\(T = - \dfrac{\hbar^2}{2m} \dfrac{d^2}{dq^2}\) є імпульсні власні функції, про які ми говорили раніше.

\[\psi_p(q) =\dfrac{1}{\sqrt{2\pi}} \exp\Big(\dfrac{ipq}{\hbar}\Big)\]

і вони підкоряються наступній ортогональності

\[\int \psi_p'*(q) \psi_p(q) dq = d(p'-p)\]

і повнота відносин

\[\int \psi_p(q) \psi_p^*(q') dp = d(q-q').\]

Написання\(\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big) \Psi(q)\) як

\[\exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big)\Psi(q) = \int dq’ \delta(q-q') \exp\Big(-\dfrac{i\tau ​V(q’)}{2\hbar}\Big)\Psi(q'),\]

і використовуючи вищевказаний вираз для\(\delta(q-q')\) дає:

\[\exp\Big(-\dfrac{i\tau ​V}{2\hbar}\Big)\Psi(q) = \int \int \psi_p(q) \psi_p^*(q') \exp\Big(-\dfrac{i\tau ​V(q’)}{2\hbar}\Big)\Psi(q') dq' dp.\]

Потім вставляємо явні вирази для\(\psi_p(q)\) і з\(\psi_p^*(q')\) точки зору

\[\psi_p(q) =\dfrac{1}{\sqrt{2\pi}} \exp\Big(\dfrac{ipq}{\hbar}\Big)\]

дає

\[\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big)\Psi(q)\]

\[= \int \int\dfrac{1}{\sqrt{2\pi}} \exp\Big(\dfrac{ipq}{\hbar}\Big)\dfrac{1}{\sqrt{2\pi}} \exp\Big(-\dfrac{ipq'}{\hbar}\Big) \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big)\Psi(q') dq' dp.\]

Тепер, дозволяючи\(\exp\Big(-\dfrac{i\tau T}{\hbar}\Big)\) діяти на\(\exp\Big(-\dfrac{i\tau V}{2\hbar}\Big) \Psi(q)\) виробляє

\[\exp\Big(-\dfrac{i\tau T}{\hbar}\Big) \exp\Big(-\dfrac{i\tau V}{2\hbar}\Big)\Psi(q) =\]

\[ \int \int \exp\Big(-\dfrac{i\tau\pi^2\hbar^2}{2m\hbar}\Big)\dfrac{1}{\sqrt{2\pi}} \exp\Big(-\dfrac{ip(q-q')}{\hbar}\Big)\dfrac{1}{\sqrt{2\pi}} \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big)\Psi(q') dq' dp.\]

Інтеграл над\(p\) вище може бути здійснений аналітично і дає

\[\exp\Big(-\dfrac{i\tau T}{\hbar}\Big) \exp\Big(-\dfrac{i\tau V}{2\hbar}\Big)\Psi(q) =\]

\[\sqrt{\dfrac{m}{2i\pi \tau\hbar}} \int \exp\Big(\dfrac{im(q-q')^2}{2\tau\hbar}\Big) \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big) \Psi(q') dq'.\]

Отже, кінцевим виразом для короткочасної поширеної хвильової функції є:

\[\Psi(q.t) = \sqrt{\dfrac{m}{2i\pi \tau\hbar}}\exp\Big(-\dfrac{i\tau V(q)}{2\hbar}\Big)\int \exp\Big(\dfrac{im(q-q')^2}{2\tau\hbar}\Big) \exp\Big(-\dfrac{i\tau V(q’)}{2\hbar}\Big)\Psi(q') dq',\]

яке є робочим рівнянням, яке використовується для обчислення\(\Psi(q,t)\) знання\(\Psi(q)\). Зверніть увагу, що все, що потрібно знати, щоб застосувати цю формулу, є потенціал\(V(q)\) у кожній точці простору. Не потрібно знати жодної з власнихфункцій гамільтоніана, щоб застосувати цей метод. Це особливо привабливо при роботі з дуже великими молекулами або молекулами в конденсованих середовищах, де по суті неможливо визначити будь-який з власних станів і де енергетичні проміжки між власними станами надзвичайно малі. Тим не менш, потрібно використовувати цю формулу знову і знову, щоб поширювати початкову хвильову функцію через багато невеликих часових кроків,\(\tau\) щоб досягти повного поширення протягом потрібного інтервалу часу\(t = P\tau\).

Оскільки цей тип техніки поширення часу є дуже активною областю досліджень у теоретичному співтоваристві, він, ймовірно, буде продовжувати вдосконалюватися та вдосконалюватися. Подальше його обговорення виходить за рамки цієї книги, тому далі в цей напрямок йти не буду. Веб-сайт професора Ненсі Макрі надає доступ до додаткової інформації про область дослідження поширення квантового часу.

Дописувачі та атрибуція

• Template:ContribSimonsTemplate:ContribHayashi