4.5: Кристалічність полімерів
- Page ID
- 19950
Ми часто думаємо про полімери у вигляді пластмас: тверді матеріали, які виконують якусь структурну функцію, наприклад пляшку з водою або деякі венеціанські жалюзі. Полімери відрізняються від багатьох інших подібних твердих речовин. Метали, наприклад, мають кристалічні структури, в яких атоми утворюють регулярно повторюваний візерунок, ряд за рядом. Полімери, навпаки, взагалі кілька аморфні. Подумайте про ситечко, наповнене приготованими спагетті, довгі ланцюжки макаронів, що петлять один над одним випадковим чином. Ось так молекули аморфних або «безформних» полімерів, як правило, розподіляються самі.

Полімери здатні утворювати більш впорядковані структури. Якби вони вирівнювалися натомість своїми довгими ланцюгами, паралельними один одному, вони змогли б стати набагато ближче один до одного, а міжмолекулярні атракціони між ланцюгами були б набагато сильнішими. Енергія системи зменшиться, тому цій більш кристалічній структурі слід за своєю суттю надавати перевагу.

Так чому ж це не завжди трапляється? Подумайте про охолодження полімеру з повністю розплавленого стану, в такому випадку структура неодмінно аморфна. У міру охолодження матеріал стає менше схожим на рідину, а потім менш м'яким. З невеликими молекулами цей перехід є відносно різким, оскільки молекули ковзають на місце, керуючись їх зміцненням міжмолекулярних атракціонів. Молекули просто повинні трохи обертатися, щоб зіткнутися з правильним напрямком, або, можливо, трохи зрушити в сторону. З полімерами перехід відбувається набагато більш поступовим, тому що ті великі, довгі ланцюги повинні ковзати один над одним і розкручуватися, щоб лежати паралельно. У якийсь момент, там просто не вистачає енергії для того, щоб продовжувати працювати свій шлях до оптимального вирівнювання. Як результат, багато полімерів є напівкристалічними, з областями, які називаються ламелями, де ділянки ланцюгів вирівняні паралельно один одному, але також з великими аморфними ділянками, які набагато більш довільно орієнтовані.
Як результат, зразок полімеру може бути на 80% аморфним, а лише 20% довжини ланцюга вирівняні в кристалічних ламелей. Незважаючи на це, ці кристалічні домени мають сильний вплив на властивості полімеру. Через більш сильних міжмолекулярних атракціонів між цими тіснішими ланцюгами ланцюги набагато менше здатні ковзати повз один одного. В результаті виходить матеріал, який міцніший і жорсткіший, і що може бути дуже важливим для надійних конструкційних матеріалів.
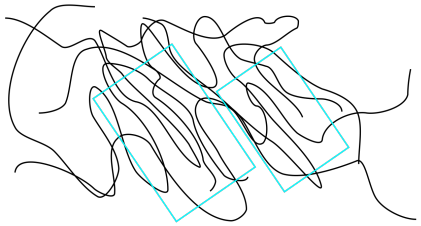
Як ми знаємо, чи містить зразок полімеру кристалічні домени? Ми можемо використовувати диференціальну скануючу калориметрію для спостереження за переходом між впорядкованою кристалічною фазою та невпорядкованою фазою розплаву з додаванням тепла. Як ми бачили, коли ми дивилися на скляний перехід, температура плавлення відображається як пік на сліді DSC. Шукати його можна при температурі вище Т г, що, як ви згадаєте, більше схоже на крок у вихідній лінії. Нижче Т г ланцюга недостатньо рухливі, щоб рухатися поза співвідношенням один з одним. У наведеному нижче прикладі ви можете побачити T g при температурі близько 128° C, а також температуру плавлення, Т м, коли подолані атракціони між ланцюгами в ламелі, при 155-160° C.
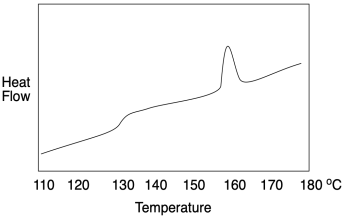
Якби це була звичайна молекулярна або елементна тверда речовина, температура плавлення була б такою ж, як і точка плавлення; матеріал плавився б при тій же температурі під час потепління, коли він застиг під час охолодження. У полімерах це зазвичай не виходить таким чином, і спостерігається гістерезис. У гістерезисі зразок змінився через попередні події, що призвело до результатів, які, здається, не відтворюються так, як ми зазвичай очікуємо. В цілому температура кристалізації, Т с, нижче температури плавлення, Т м. Це тому, що, коли матеріал плавиться, ланцюги виходять з вирівнювання один з одним і через заплутування ланцюга їм заважають знову повернутися в вирівнювання один з одним, що призводить до затримки кристалізації.
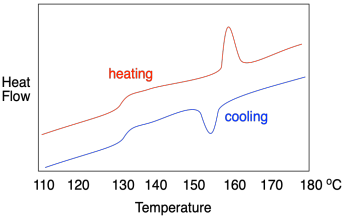
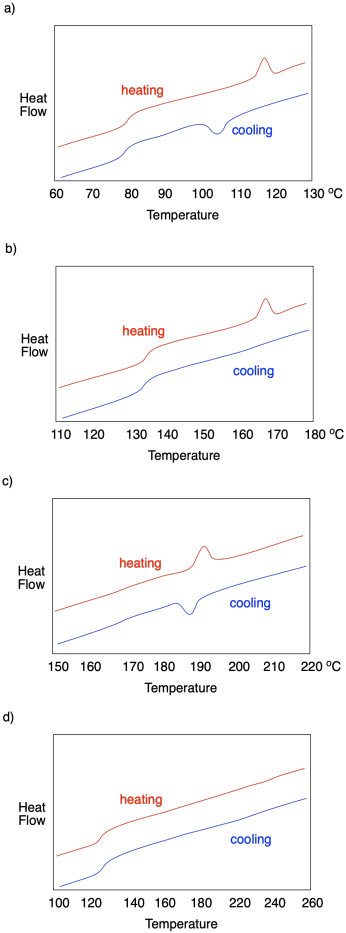
Опишіть, що спостерігається в кожному з наступних слідів DSC.
Кристалічність можна промацати і іншими способами. Класичний підхід - за допомогою рентгенівської дифракції. Коли рентгенівські промені проходять через впорядковані матеріали, вони породжують дифракційні візерунки, яскраві плями в просторі, де рикохетингові рентгенівські промені конструктивно заважали один одному, яскраво сяючи серед чорноти, де рентгенівські промені зазнали руйнівного втручання.
На малюнку нижче зображений мультфільм рентгенівського дифракційного малюнка. Це може бути знято цифровою камерою або, в попередні дні, аркушем фотоплівки. Яскраві плями виникають внаслідок рентгенівських променів, що розсіюються з середини, де вони зіткнулися зі зразком. Посередині чорне коло блокує оригінальний рентгенівський промінь, який інакше був би занадто яскравим, щоб дозволити спостерігати ці плями навколо нього.

Дані рентгенівського дифракційного експерименту подаються в програму, яка може математично деконволютувати, чому плями з'явилися там, де вони зробили. Процес порівнювали з киданням каменю через плече у ставок, а потім спостерігаючи за брижами, щоб вирішити, де камінь повинен бути. З одним каменем, це повинно бути досить легко. Ви знайдете камінь в центрі кола брижі. З двома або більше каменями інтерференційні візерунки роблять брижі більш складними, і тому може знадобитися більше роботи, щоб визначити, де кожен камінь лежить у ставку.
Зображення нижче ілюструє результати відносно простого експерименту рентгенівської дифракції, який зазвичай використовується із зразками кристалічних полімерів. Методика називається ширококутним рентгенівським розсіюванням, або WAXS. Він просто повідомляє кут, під яким спостерігається інтенсивність розсіювання щодо початкового рентгенівського променя. Цей кут відповідає відстані між атомами в зразку, що в даному випадку зазвичай відповідає відстані між паралельними полімерними ланцюгами. Іноді може бути більше одного піку, але цей приклад простий для початку.
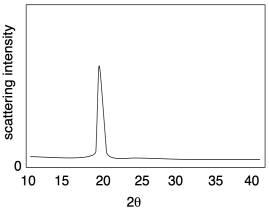
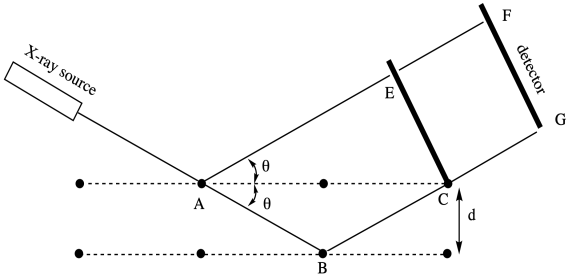
Зв'язок між цим кутом розсіювання та міжатомною відстанню дається Законом Брегга, фундаментальною відправною точкою в рентгенівській кристалографії, вперше вираженою сером Вільямом Бреггом та його сином, сером Лоуренсом Бреггом. У законі зазначено, що:
\[nλ = 2d\sin θ \label{bragg1}\]
в якому n є цілим числом (зазвичай вважається 1), лямбда - довжина хвилі використовуваного рентгенівського випромінювання (зазвичай 1.541 Å, хоча можливі інші), d - відстань між регулярно повторюваними атомами і θ - кут розсіювання.
Переставляючи рівняння\ ref {bragg1}, знаходимо:
\[d = \dfrac{1.541}{2\sin θ}\]
Іншими словами, відстань між атомами обернено пропорційно куту розсіювання. Чим більше кут, тим менше відстань.
У кожному з наступних випадків визначте, який зразок (А або В) має більш високий вміст кристалів.
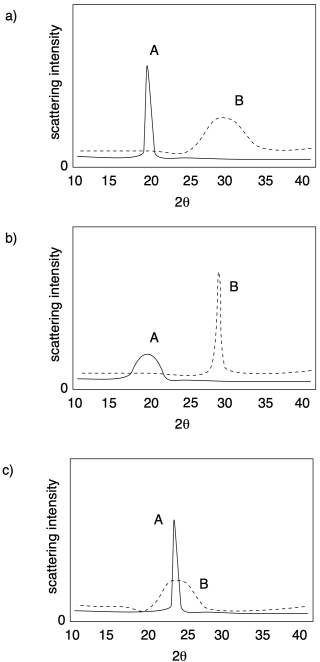
Проблема РП5.1.