9.5: Кінетико-молекулярна теорія

Цілі навчання

• Стан постулатів кінетико-молекулярної теорії
• Використовуйте постулати цієї теорії для пояснення газових законів

Газові закони, які ми бачили до цього моменту, а також ідеальне рівняння газу, є емпіричними, тобто вони були отримані з експериментальних спостережень. Математичні форми цих законів близько описують макроскопічну поведінку більшості газів при тисках менше приблизно 1 або 2 атм. Хоча газові закони описують відносини, які були перевірені багатьма експериментами, вони не говорять нам, чому гази слідують цим відносинам.

Кінетична молекулярна теорія (КМТ) - це проста мікроскопічна модель, яка ефективно пояснює газові закони, описані в попередніх модулів цієї глави. Ця теорія заснована на наступних п'яти постулатах, описаних тут. (Примітка: Термін «молекула» буде використовуватися для позначення окремих хімічних видів, що складають газ, хоча деякі гази складаються з атомних видів, наприклад, благородних газів.)

1. Гази складаються з молекул, які знаходяться в безперервному русі, рухаються прямими лініями і змінюють напрямок лише при зіткненні з іншими молекулами або зі стінками контейнера.
2. Молекули, що складають газ, незначні порівняно з відстанями між ними.
3. Тиск, який чинить газ у контейнері, виникає внаслідок зіткнень між молекулами газу та стінками контейнера.
4. Молекули газу не надають ніяких привабливих або відштовхуючих сил один на одного або на стінки контейнера, тому їх зіткнення еластичні (не передбачають втрати енергії).
5. Середня кінетична енергія молекул газу пропорційна температурі кельвіна газу.

Тест КМТ та його постулатів - це його здатність пояснювати та описувати поведінку газу. Різні газові закони можуть бути виведені з припущень КМТ, які змусили хіміків вважати, що припущення теорії точно представляють властивості молекул газу. Спочатку ми розглянемо окремі закони газу (закони Бойла, Чарльза, Амонтона, Авогадро та Далтона) концептуально, щоб побачити, як KMT пояснює їх. Потім ми більш ретельно розглянемо співвідношення між молекулярними масами, швидкостями та кінетичними енергіями з температурою та пояснимо закон Грема.

Кінетико-молекулярна теорія пояснює поведінку газів, частина I

Згадуючи, що тиск газу чиниться швидко рухомими молекулами газу і безпосередньо залежить від кількості молекул, що потрапляють на одиницю площі стінки за одиницю часу, ми бачимо, що КМТ концептуально пояснює поведінку газу наступним чином:

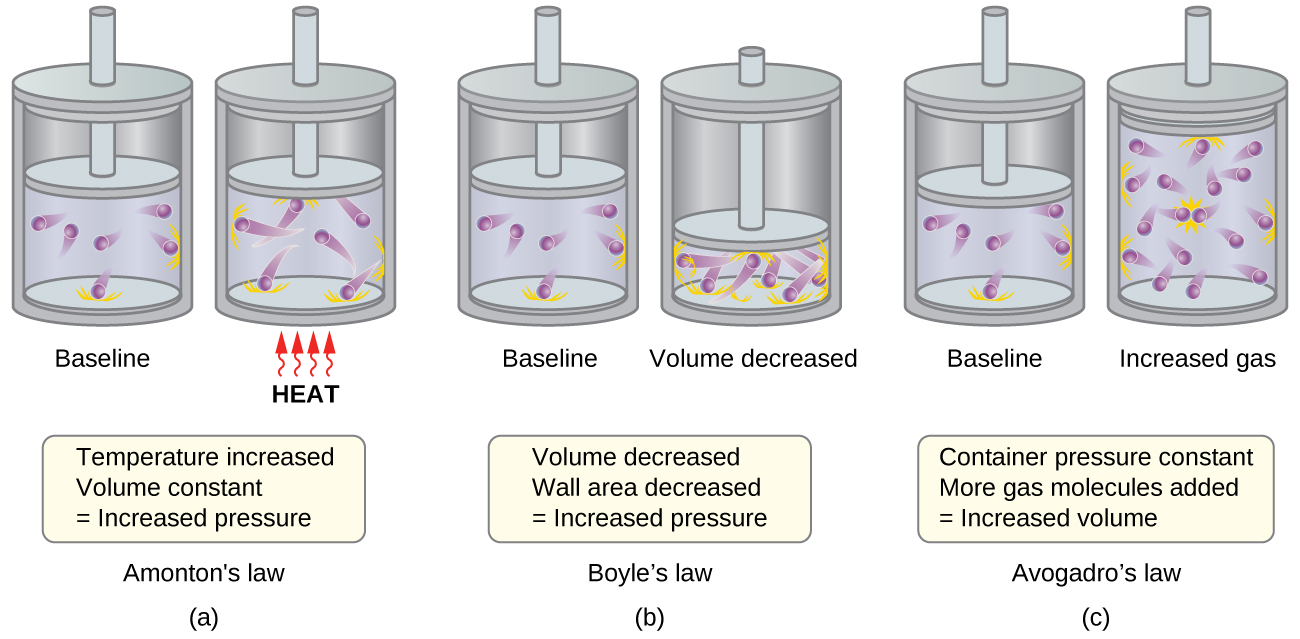
• Закон Амонтона. Якщо температура підвищена, то середня швидкість і кінетична енергія молекул газу збільшуються. Якщо обсяг утримується постійним, то підвищена швидкість молекул газу призводить до більш частих і більш силових зіткнень зі стінками ємності, тому підвищуючи тиск (рис.\(\PageIndex{1a}\)).
• Закон Чарльза. Якщо температура газу підвищена, постійний тиск може підтримуватися тільки в тому випадку, якщо обсяг, зайнятий газом, збільшується. Це призведе до більших середніх відстаней, пройдених молекулами для досягнення стінок контейнера, а також збільшення площі поверхні стінки. Ці умови зменшать як частоту зіткнень молекулярної стінки, так і кількість зіткнень на одиницю площі, комбіновані ефекти яких врівноважують вплив підвищених сил зіткнення за рахунок більшої кінетичної енергії при більш високій температурі.
• Закон Бойла. Якщо обсяг газу зменшується, площа стінки контейнера зменшується і частота зіткнення молекули стінки збільшується, обидва з яких збільшують тиск, що чиниться газом (рис.\(\PageIndex{1b}\)).
• Закон Авогадро. При постійному тиску і температурі частота і сила зіткнень молекулярно-стінкових постійних. В таких умовах збільшення кількості газоподібних молекул зажадає пропорційного збільшення об'єму ємності, щоб дати зменшення кількості зіткнень на одиницю площі для компенсації підвищеної частоти зіткнень (рис.\(\PageIndex{1c}\)).
• Закон Далтона. Через великі відстані між ними молекули одного газу в суміші бомбардують стінки ємності з однаковою частотою, незалежно від того, присутні інші гази чи ні, а загальний тиск газової суміші дорівнює сумі (парціальних) тисків окремих газів.

Малюнок\(\PageIndex{1}\): (а) При підвищенні температури газу тиск газу збільшується через збільшення сили і частоти молекулярних зіткнень. (б) При зменшенні об'єму тиск газу збільшується через збільшення частоти молекулярних зіткнень. (c) Коли кількість газу збільшується при постійному тиску, обсяг збільшується, щоб отримати постійну кількість зіткнень на одиницю площі стінки в одиницю часу.

На цьому малюнку показані 3 пари поршнів і циліндрів. У, який позначений як «Закон Чарльза», поршень розташований для першого циліндра так, що трохи більше половини доступного обсягу містить 6 фіолетових сфер з стежками позаду них. Траси вказують на рух. Помаранчеві риски простягаються від внутрішньої поверхні циліндра, де зіткнулися сфери. Цей циліндр має маркування «Базова лінія». У другому циліндрі поршень знаходиться в тому ж положенні, а мітка «Тепло» позначена червоним великим текстом. Чотири червоні стрілки з хвилястими стеблами спрямовані вгору до основи циліндра. Шість фіолетових сфер мають довші стежки позаду них, а кількість помаранчевих рисок, що вказують на точки зіткнення зі стінками контейнера, збільшилася. Прямокутник під діаграмою говорить: «Температура збільшена, об'єм константа дорівнює підвищеному тиску». У b, який позначений «Закон Бойла», перший, базовий циліндр показаний ідентичний першому циліндру в а У другому циліндрі поршень був переміщений, зменшуючи обсяг, доступний для 6 фіолетових сфер до половини початкового об'єму. Шість фіолетових сфер мають довші стежки позаду них, а кількість помаранчевих рисок, що вказують на точки зіткнення зі стінками контейнера, збільшилася. Цей другий циліндр має маркування «Обсяг зменшився». Прямокутник під діаграмою говорить: «Обсяг зменшився, площа стіни зменшилася дорівнює підвищеному тиску». У c, який позначений «Закон Авогадро», перший, базовий циліндр показаний ідентичний першому циліндру в а У другому циліндрі кількість фіолетових сфер змінилася з 6 до 12, а обсяг збільшився вдвічі. Цей другий балон має маркування «Збільшений газ». Прямокутник під діаграмою говорить: «При постійному тиску додається більше молекул газу дорівнює збільшеному об'єму».

Молекулярні швидкості та кінетична енергія

Попереднє обговорення показало, що KMT якісно пояснює поведінку, описану різними газовими законами. Постулати цієї теорії можуть застосовуватися більш кількісно, щоб вивести ці індивідуальні закони. Для цього потрібно спочатку подивитися на швидкості і кінетичні енергії молекул газу, а також температуру проби газу.

У зразку газу окремі молекули мають широко різну швидкість; однак через величезну кількість молекул та зіткнень, розподіл молекулярної швидкості та середня швидкість постійні. Цей молекулярний розподіл швидкості відомий як розподіл Максвелла-Больцмана, і він зображує відносні числа молекул у об'ємному зразку газу, який має задану швидкість (рис.\(\PageIndex{2}\)).

Малюнок\(\PageIndex{2}\): Молекулярний розподіл швидкості для газу кисню при 300 К наведено тут. Дуже мало молекул рухається з дуже низькою або дуже високою швидкістю. Кількість молекул з проміжними швидкостями швидко зростає до максимуму, що є найбільш ймовірною швидкістю, потім швидко падає. Зауважимо, що найбільш ймовірна швидкість, ν _p, трохи менше 400 м/с, тоді як середня середня квадратна швидкість, u _rms, ближче до 500 м/с.

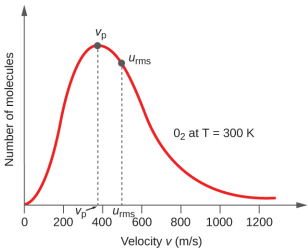
Кінетична енергія (КЕ) частинки маси (m) і швидкості (u) задається:

\[\ce{KE}=\dfrac{1}{2}mu^2 \nonumber \]

Висловлювання маси в кілограмах і швидкості в метрах в секунду дасть енергетичні значення в одиницях джоулів (J = кг м ² с ^—2). Для боротьби з великою кількістю молекул газу ми використовуємо середні показники як для швидкості, так і для кінетичної енергії. У КМТ середньоквадратична швидкість частинки, u _rms, визначається як квадратний корінь середнього квадратів швидкостей з n = кількість частинок:

\[u_\ce{rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u^2_1+u^2_2+u^2_3+u^2_4+…}{n}} \nonumber \]

Середня кінетична енергія, KE _avg, тоді дорівнює:

\[\mathrm{KE_{avg}}=\dfrac{1}{2}mu^2_\ce{rms} \nonumber \]

KE _{середнє} значення колекції молекул газу також прямо пропорційно температурі газу і може бути описано рівнянням:

\[\mathrm{KE_{avg}}=\dfrac{3}{2}RT \nonumber \]

де R - газова постійна, а T - температура Кельвіна. При використанні в цьому рівнянні відповідною формою газової константи є 8,314 Дж моль ^{-1 К -1} (8,314 кг м ² с ^{— 2} моль ^-1 К ^—1). Ці два окремі рівняння для KE _avg можуть бути об'єднані та перебудовані, щоб отримати зв'язок між молекулярною швидкістю та температурою:

\[\dfrac{1}{2}mu^2_\ce{rms}=\dfrac{3}{2}RT \nonumber \]

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}} \label{RMS} \]

Приклад\(\PageIndex{1}\): Calculation of u_rms

Обчисліть середньоквадратичну швидкість для молекули азоту при 30 °С.

Рішення

Перетворіть температуру в Кельвін:

\[30°C+273=303\: K \nonumber \]

Визначаємо масу молекули азоту в кілограмах:

\[\mathrm{\dfrac{28.0\cancel{g}}{1\: mol}×\dfrac{1\: kg}{1000\cancel{g}}=0.028\:kg/mol} \nonumber \]

Замініть змінні та константи у формулі середньоквадратичної швидкості (Equation\ ref {RMS}), замінивши Джоулі еквівалентом kg m ² s ^—2:

\[ \begin{align*} u_\ce{rms} &= \sqrt{\dfrac{3RT}{m}} \\ u_\ce{rms} &=\sqrt{\dfrac{3(8.314\:J/mol\: K)(303\: K)}{(0.028\:kg/mol)}} \\ &=\sqrt{2.70 \times 10^5\:m^2s^{−2}} \\ &= 519\:m/s \end{align*} \nonumber \]

Вправа\(\PageIndex{1}\)

Обчисліть середньоквадратичну швидкість для молекули кисню при -23 °С.

Відповідь

441 м/с

Якщо температура газу збільшується, його _{середнє} значення KE збільшується, більше молекул мають більш високі швидкості і менше молекул мають менші швидкості, а розподіл зміщується в бік більш високих швидкостей загалом, тобто вправо. Якщо температура знижується, KE _avg зменшується, більше молекул мають менші швидкості і менше молекул мають більш високі швидкості, а розподіл зміщується в бік більш низьких швидкостей загалом, тобто вліво. Така поведінка проілюстрована для газу азоту на рис\(\PageIndex{3}\).

Малюнок\(\PageIndex{3}\): Розподіл молекулярної швидкості для газу азоту (N ₂) зміщується вправо і сплющується з підвищенням температури; він зміщується вліво і посилюється зі зниженням температури.

Показано графік з чотирма позитивними або правими кривими різної висоти. Горизонтальна вісь позначена як «Швидкість v (m ділиться на s)». Ця вісь позначена кроком 500, починаючи з 0 і простягаючись до 1500. Вертикальна вісь позначена як «Фракція молекул». Мітка «N indexpt 2» з'являється у відкритому просторі у верхній правій частині графіка. Найвищий і вузький з цих кривих маркується, «100 К.» Його правий кінець, здається, торкається горизонтальної осі близько 700 м на с, за ним слідує трохи ширша крива, яка позначена як «200 К», тобто приблизно три чверті висоти початкової кривої. Його правий кінець, здається, торкається горизонтальної осі близько 850 м на с. третя крива значно ширше і лише близько половини висоти початкової кривої. Він має маркування, «500 К.» Його правий кінець, здається, торкається горизонтальної осі близько 1450 м на с. остаточна крива становить лише приблизно одну третину висоти початкової кривої. Вона набагато ширше інших, настільки, що її правий кінець ще не дійшов до горизонтальної осі. Ця крива позначена, «1000 К.»

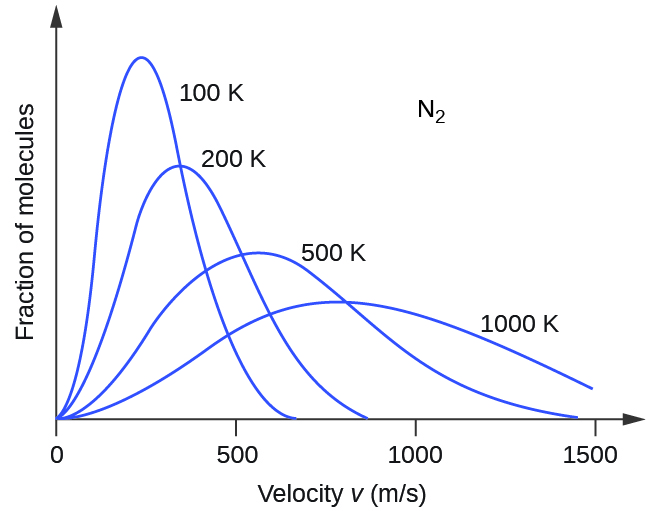
При заданій температурі всі гази мають однакове KE _avg для своїх молекул. Гази, що складаються з більш легких молекул, мають більш високошвидкісні частинки і більш високу u _{середньоквадратичну}, з розподілом швидкості, який досягає максимуму при відносно більших швидкостях Гази, що складаються з більш важких молекул, мають більше низькошвидкісних частинок, менший u _{середньоквадратичне} значення та розподіл швидкості, який досягає максимуму при відносно менших швидкостях. Цю тенденцію демонструють дані для серії благородних газів, показані на рис\(\PageIndex{4}\).

Малюнок\(\PageIndex{4}\): Молекулярна швидкість безпосередньо пов'язана з молекулярною масою. При заданій температурі більш легкі молекули рухаються в середньому швидше, ніж більш важкі молекули.

Графік показаний з чотирма позитивними або правими кривими різної висоти. Горизонтальна вісь позначена як «Швидкість v (m ділиться на s)». Ця вісь позначена кроком 500, починаючи з 0 і простягаючись до 3000. Вертикальна вісь позначена як «Фракція молекул». Найвищий і вузький з цих кривих маркується «X e». Його правий кінець, здається, торкається горизонтальної осі близько 600 м на с, за ним слідує трохи ширша крива, яка позначена «A r», тобто приблизно на половину висоти початкової кривої. Його правий кінець, здається, торкається горизонтальної осі близько 900 м на с. третя крива значно ширша і трохи більше третини висоти початкової кривої. Він позначений, «N e.» Його правий кінець, здається, торкається горизонтальної осі близько 1200 м на с. кінцева крива становить лише близько однієї четвертої висоти початкової кривої. Він набагато ширше інших, настільки, що його право досягає горизонтальної осі близько 2500 м на с. ця крива маркується «Н е».

Газовий тренажер може бути використаний для вивчення впливу температури на молекулярні швидкості. Вивчіть «енергетичні гістограми» симулятора (розподіли молекулярної швидкості) та «інформацію про види» (яка дає середні значення швидкості) для молекул різних мас при різних температурах.

Кінетико-молекулярна теорія пояснює поведінку газів, частина II

Згідно із законом Грема, молекули газу знаходяться в швидкому русі, а самі молекули невеликі. Середня відстань між молекулами газу велика в порівнянні з розміром молекул. Як наслідок, молекули газу можуть легко переміщатися повз один одного і дифузно з відносно швидкими темпами.

Швидкість випоту газу безпосередньо залежить від (середньої) швидкості його молекул:

\[\textrm{effusion rate} ∝ u_\ce{rms} \nonumber \]

Використовуючи це співвідношення та рівняння, що стосується молекулярної швидкості до маси, закон Грема може бути легко виведений, як показано тут:

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}} \nonumber \]

\[m=\dfrac{3RT}{u^2_\ce{rms}}=\dfrac{3RT}{\overline{u}^2} \nonumber \]

\[\mathrm{\dfrac{effusion\: rate\: A}{effusion\: rate\: B}}=\dfrac{u_\mathrm{rms\:A}}{u_\mathrm{rms\:B}}=\dfrac{\sqrt{\dfrac{3RT}{m_\ce{A}}}}{\sqrt{\dfrac{3RT}{m_\ce{B}}}}=\sqrt{\dfrac{m_\ce{B}}{m_\ce{A}}} \nonumber \]

Таким чином, співвідношення швидкостей випоту виводиться обернено пропорційним співвідношенню квадратних коренів їх мас. Це те ж відношення, яке спостерігається експериментально і виражається як закон Грема.

Резюме

Кінетична молекулярна теорія - це проста, але дуже ефективна модель, яка ефективно пояснює ідеальну поведінку газу. Теорія передбачає, що гази складаються з широко відокремлених молекул мізерно невеликого обсягу, які знаходяться в постійному русі, пружно стикаються один з одним і стінками їх ємності з середніми швидкостями, визначеними їх абсолютними температурами. Окремі молекули газу демонструють діапазон швидкостей, розподіл цих швидкостей залежить від температури газу і маси його молекул.

Ключові рівняння

• \(u_\ce{rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u^2_1+u^2_2+u^2_3+u^2_4+…}{n}}\)
• \(\mathrm{KE_{avg}}=\dfrac{3}{2}RT\)
• \(u_\ce{rms}=\sqrt{\dfrac{3RT}{m}}\)

Резюме

кінетична молекулярна теорія

теорія, заснована на простих принципах і припущеннях, що ефективно пояснює ідеальну поведінку газу

середньоквадратична швидкість (u _rms)

міра середньої швидкості для групи частинок, розрахована як квадратний корінь середньої квадратної швидкості