9.6: Неідеальна поведінка газу

Last updated
Save as PDF

Page ID: 22739

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Опишіть фізичні фактори, що призводять до відхилень від ідеальної поведінки газу
Поясніть, як ці фактори представлені в рівнянні ван дер Ваальса
Визначте стисливість (Z) і опишіть, як її зміна з тиском відображає неідеальну поведінку
Кількісна оцінка неідеальної поведінки шляхом порівняння розрахунків властивостей газу з використанням закону ідеального газу та рівняння ван дер Ваальса

До теперішнього часу закон ідеального газу, PV = nRT, застосовувався до безлічі різних типів проблем, починаючи від стехіометрії реакції та емпіричних та молекулярних формул до визначення щільності та молярної маси газу. Однак, як згадувалося в попередніх модулів цієї глави, поведінка газу часто є неідеальною, а це означає, що спостережувані співвідношення між його тиском, об'ємом та температурою не точно описані газовими законами. У цьому розділі розглядаються причини цих відхилень від ідеального газового поведінки.

Одним із способів, за яким можна судити про точність PV = nRT, є порівняння фактичного обсягу 1 моля газу (його молярний об'єм, Vm) з молярним об'ємом ідеального газу при тій же температурі і тиску. Це співвідношення називається коефіцієнтом стисливості (Z) при:

\[\mathrm{Z=\dfrac{molar\: volume\: of\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}{molar\: volume\: of\: ideal\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}}=\left(\dfrac{PV_m}{RT}\right)_\ce{measured} \nonumber \]

Таким чином, ідеальна поведінка газу вказується, коли це співвідношення дорівнює 1, а будь-яке відхилення від 1 є свідченням неідеальної поведінки. \(\PageIndex{1}\)На малюнку показані графіки Z у великому діапазоні тиску для декількох загальних газів.

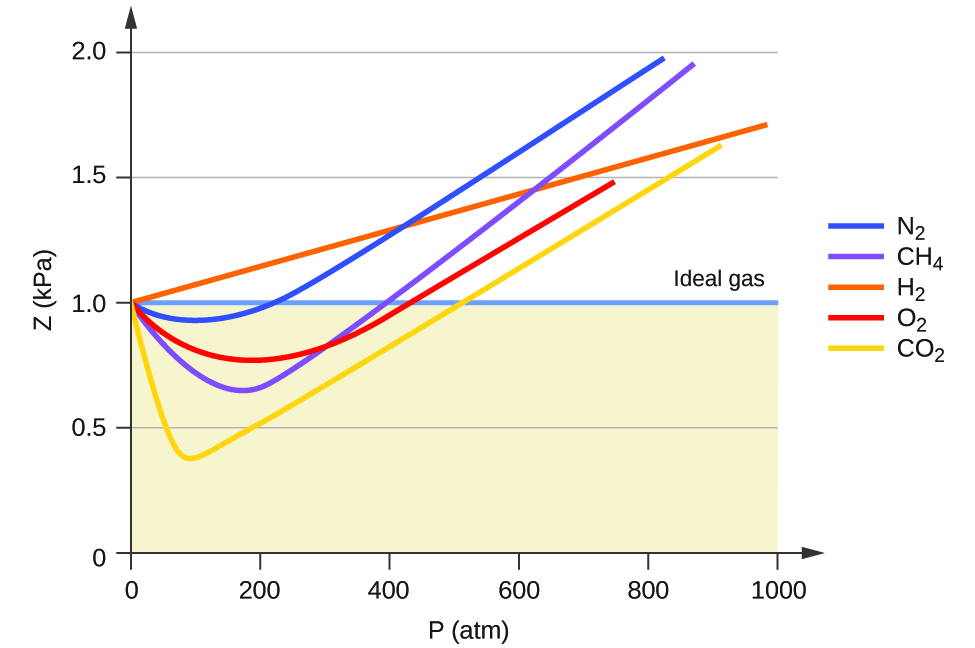
Малюнок\(\PageIndex{1}\): Графік коефіцієнта стисливості (Z) проти тиску показує, що гази можуть виявляти значні відхилення від поведінки, передбаченої законом ідеального газу.

Як видно з малюнка\(\PageIndex{1}\), ідеальний закон газу не описує поведінку газу добре при відносно високих тисках. Щоб визначити, чому це так, розглянемо відмінності між реальними властивостями газу і тим, що очікується від гіпотетичного ідеального газу.

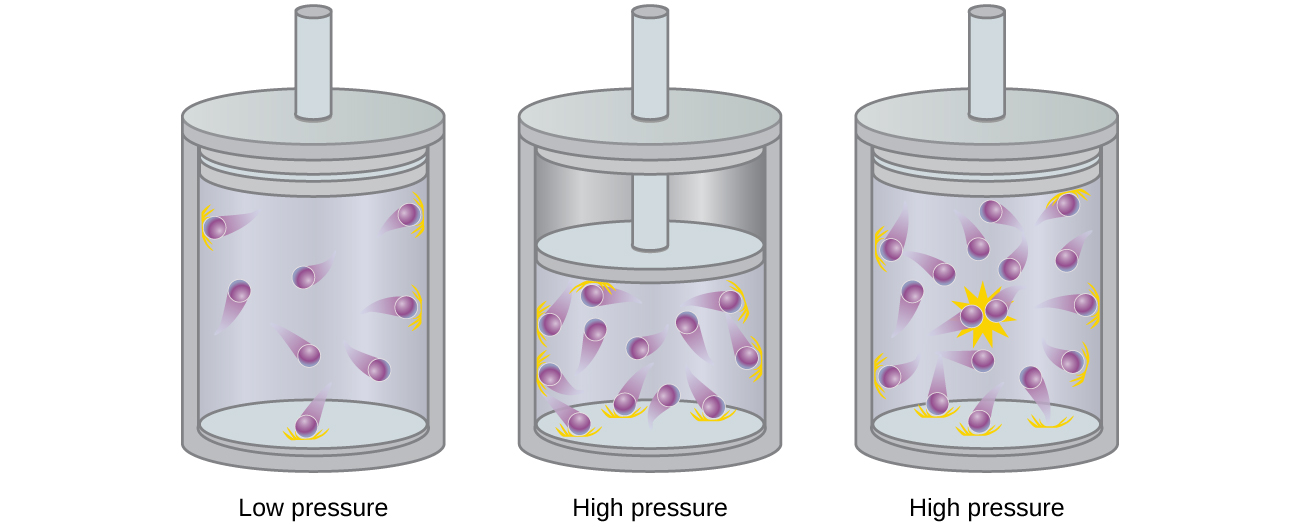
Частинки гіпотетичного ідеального газу не мають значного обсягу і не притягують і не відштовхують один одного. Загалом, реальні гази наближають таку поведінку при відносно низьких тисках і високих температурах. Однак при високих тисках молекули газу скупчуються ближче один до одного, і кількість порожнього простору між молекулами зменшується. При цих більш високих тисках обсяг самих молекул газу стає відчутним щодо загального обсягу, зайнятого газом (рис.\(\PageIndex{2}\)). Таким чином, газ стає менш стисливим при цих високих тисках, і хоча його обсяг продовжує зменшуватися зі збільшенням тиску, це зниження не є пропорційним, як передбачено законом Бойла.

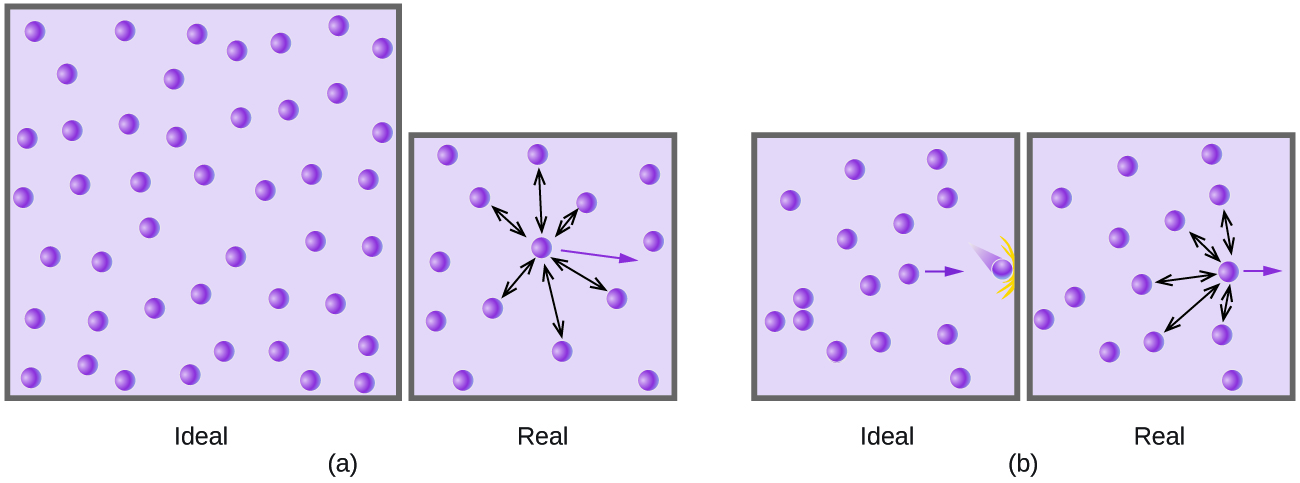
Малюнок\(\PageIndex{2}\): Підвищення тиску газу збільшує частку його об'єму, яку займають молекули газу, і робить газ менш стисливим.

При відносно низькому тиску молекули газу практично не мають тяжіння один до одного, оскільки вони (в середньому) настільки далеко один від одного, і вони поводяться майже як частинки ідеального газу. При більш високих тисках, однак, сила тяжіння також вже не незначна. Ця сила тягне молекули трохи ближче один до одного, трохи зменшуючи тиск (якщо обсяг постійний) або зменшуючи обсяг (при постійному тиску) (рис.\(\PageIndex{3}\)). Ця зміна більш виражена при низьких температурах, оскільки молекули мають нижчі KE щодо сил притягання, і тому вони менш ефективні в подоланні цих атракціонів після зіткнення один з одним.

Малюнок\(\PageIndex{3}\): (а) Атракціони між молекулами газу служать для зменшення обсягу газу при постійному тиску порівняно з ідеальним газом, молекули якого не відчувають привабливих сил. (b) Ці привабливі сили зменшать силу зіткнень між молекулами та стінками контейнера, тим самим зменшуючи тиск, що чиниться порівняно з ідеальним газом.

Існує кілька різних рівнянь, які краще наближають поведінку газу, ніж ідеальний закон газу. Перший, і найпростіший, з них був розроблений голландським вченим Йоханнесом ван дер Ваальсом в 1879 році. Рівняння ван дер Ваальса покращує закон ідеального газу, додаючи два члени: один для обліку об'єму молекул газу, а інший для привабливих сил між ними.

На цьому малюнку показано рівняння P V дорівнює n R T, з P синім текстом і V червоним текстом. За цим рівнянням слідує стрілка, що вказує вправо. Слідом за цією стрілкою праворуч у синьому тексті з'являється рівняння (P мінус a n верхній індекс 2 ділиться на V квадрат)», за яким слідує червоний текст (V мінус n b). Далі слід чорним текстом з рівним n R T. Під другим рівнянням з'являється мітка «Корекція молекулярного тяжіння», яка пов'язана з відрізком лінії до V квадрату. Друга мітка «Корекція об'єму молекул» аналогічно з'єднана з n b, яка відображається червоним кольором.

Константа a відповідає силі тяжіння між молекулами конкретного газу, а постійна b відповідає розміру молекул конкретного газу. «Корекція» до терміну тиску в законі ідеального газу є\(\dfrac{n^2a}{V^2}\), а «корекція» до обсягу - nb. Зверніть увагу, що коли V відносно великий, а n відносно малий, обидва ці терміни корекції стають незначними, а рівняння ван дер Ваальса зводиться до ідеального закону газу, PV = nRT. Такий стан відповідає газу, при якому відносно невелика кількість молекул займає відносно великий обсяг, тобто газ при відносно низькому тиску. Експериментальні значення констант ван дер Ваальса деяких загальних газів наведені в табл\(\PageIndex{1}\).

Таблиця\(\PageIndex{1}\): Значення констант ван дер Ваальса для деяких загальних газів
Газ	а (Л ² атм/моль ²)	b (л/моль)
N ₂	1.39	0.0391
О ₂	1.36	0.0318
СО ₂	3.59	0.0427
Н ₂ О	5.46	0.0305
Він	0.0342	0.0237
ККл ₄	20.4	0.1383

При низьких тисках корекція на міжмолекулярне притягання, а, важливіша за ту, що для молекулярного об'єму, б. При високих тисках і малих обсягах корекція обсягу молекул стає важливою, оскільки самі молекули нестисливі і становлять помітну частку загального обсягу. При деякому проміжному тиску дві поправки мають протилежні впливи, і газ, здається, дотримується співвідношення, заданого PV = nRT в невеликому діапазоні тисків. Така поведінка відображається «провалами» в декількох кривих стисливості, показаних на малюнку\(\PageIndex{1}\). Приваблива сила між молекулами спочатку робить газ більш стисливим, ніж ідеальний газ, так як тиск підвищується (Z зменшується зі збільшенням P). При дуже високих тисках газ стає менш стисливим (Z збільшується з P), так як молекули газу починають займати все більш значну частку загального обсягу газу.

Власне кажучи, ідеальне рівняння газу добре функціонує тоді, коли міжмолекулярні атракціони між молекулами газу незначні, а самі молекули газу не займають помітну частину всього об'єму. Цим критеріям задовольняють в умовах низького тиску і високої температури. За таких умов газ, як кажуть, поводиться ідеально, а відхилення від газових законів досить малі, щоб їх можна було знехтувати - це, однак, дуже часто не так.

Приклад\(\PageIndex{1}\): Comparison of Ideal Gas Law and van der Waals Equation

Колба об'ємом 4,25 л містить 3,46 моль СО ₂ при 229 °С Розрахуйте тиск цієї проби СО ₂:

від ідеального закону газу
з рівняння ван дер Ваальса
Поясніть причину (и) різниці.

Рішення

(а) З ідеального закону газу:

\(P=\dfrac{nRT}{V}=\mathrm{\dfrac{3.46\cancel{mol}×0.08206\cancel{L}atm\cancel{mol^{−1}}\cancel{K^{−1}}×502\cancel{K}}{4.25\cancel{L}}=33.5\:atm}\)

(b) З рівняння ван дер Ваальса:

\(\left(P+\dfrac{n^2a}{V^2}\right)×(V−nb)=nRT⟶P=\dfrac{nRT}{(V−nb)}−\dfrac{n^2a}{V^2}\)

\(P=\mathrm{\dfrac{3.46\:mol×0.08206\:L\:atm\:mol^{−1}\:K^{−1}×502\: K}{(4.25\:L−3.46\:mol×0.0427\:L\:mol^{−1})}−\dfrac{(3.46\:mol)^2×3.59\:L^2\:atm\:mol^2}{(4.25\:L)^2}}\)

Це, нарешті, дає P = 32,4 атм.

(c) Це не сильно відрізняється від значення закону ідеального газу, оскільки тиск не дуже високий, а температура не дуже низька. Значення дещо інше, оскільки молекули CO ₂ мають певний обсяг та атракціони між молекулами, а ідеальний закон газу передбачає, що вони не мають об'єму чи атракціонів.

Вправа\(\PageIndex{1}\)

Колба об'ємом 560 мл містить 21,3 г N ₂ при 145 °С Розрахуйте тиск N ₂:

від ідеального закону газу
з рівняння ван дер Ваальса
Поясніть причину (и) різниці.

Відповідь: 46,562 атм
Відповідь б: 46,594 атм
Відповідь c: Рівняння ван дер Ваальса враховує обсяг самих молекул газу, а також міжмолекулярних атракціонів.

Резюме

Молекули газу мають кінцевим об'ємом і відчувають сили тяжіння один до одного. Отже, поведінка газу не обов'язково добре описується законом ідеального газу. В умовах низького тиску та високої температури ці фактори незначні, ідеальне рівняння газу - це точний опис поведінки газу, а газ, як кажуть, демонструє ідеальну поведінку. Однак при більш низьких температурах і більш високих тисках потрібні поправки на молекулярний об'єм і молекулярні атракціони для обліку кінцевих молекулярних розмірів і сили привабливості. Рівняння ван дер Ваальса є модифікованою версією закону ідеального газу, який може бути використаний для обліку неідеальної поведінки газів в цих умовах.

Ключові рівняння

\(\mathrm{Z=\dfrac{molar\:volume\: of\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}{molar\: volume\: of\: ideal\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}}=\left(\dfrac{P×V_m}{R×T}\right)_\ce{measured}\)
\(\left(P+\dfrac{n^2a}{V^2}\right)×(V−nb)=nRT\)

Глосарій

коефіцієнт стисливості (Z): відношення експериментально виміряного молярного об'єму газу до його молярного об'єму, що обчислюється з рівняння ідеального газу

рівняння ван дер Ваальса: модифікований варіант рівняння ідеального газу, що містить додаткові терміни для обліку неідеальної поведінки газу