6.2: Модель Бора

Last updated
Save as PDF

Page ID: 22495

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Опишіть модель Бора атома водню
Використовуйте рівняння Рідберга для обчислення енергій світла, випромінюваного або поглиненого атомами водню

Слідом за роботою Ернеста Резерфорда і його колег на початку ХХ століття добре склалася картина атомів, що складаються з крихітних щільних ядер, оточених більш легкими і навіть дрібними електронами, які постійно рухаються навколо ядра. Ця картина отримала назву планетарної моделі, оскільки вона зображувала атом як мініатюрну «сонячну систему» з електронами, що обертаються навколо ядра, як планети, що обертаються навколо Сонця. Найпростішим атомом є водень, що складається з одного протона як ядра, навколо якого рухається один електрон. Електростатична сила, що притягує електрон до протона, залежить тільки від відстані між двома частинками.

\[ F_{gravity} = G \dfrac{ m_1 m_2}{r^2} \nonumber \]

із

\(G\)є гравітаційною константою
\(m_1\)і\(m_2\) є масами частинок 1 і 2 відповідно
\(r\)відстань між двома частинками

Електростатична сила має ту ж форму, що і сила гравітації між двома масовими частинками, за винятком того, що електростатична сила залежить від величин зарядів на частинках (+1 для протона і −1 для електрона) замість величин мас частинок, що керують гравітаційною сила.

\[ F_{electrostatic} = k \dfrac{ m_1 m_2}{r^2} \nonumber \]

із

\(k\)є постійною
\(m_1\)і\(m_2\) є масами частинок 1 і 2 відповідно
\(r\)відстань між двома частинками

Оскільки сили можуть бути отримані з потенціалів, зручно працювати з потенціалами замість цього, оскільки вони є формами енергії. Електростатичний потенціал ще називають кулонівським потенціалом. Оскільки електростатичний потенціал має ту ж форму, що і гравітаційний потенціал, згідно з класичною механікою, рівняння руху повинні бути аналогічними, при цьому електрон рухається навколо ядра по кругових або еліптичних орбітах (звідси і мітка «планетарна» модель атома). Потенціали форми V (r), які залежать тільки від радіальної відстані\(r\), відомі як центральні потенціали. Центральні потенціали мають сферичну симетрію, і тому замість того, щоб вказувати положення електрона в звичайних декартових координатах (x, y, z), зручніше використовувати полярні сферичні координати, центровані у ядра, що складаються з лінійної координати r і дві кутові координати, зазвичай задаються грецькими літерами theta (θ) і phi (Φ). Ці координати схожі на ті, що використовуються в GPS-пристроях та більшості смартфонів, які відстежують позиції на нашій (майже) сферичній землі, з двома кутовими координатами, визначеними широтою та довготою, та лінійною координатою, визначеною висотою рівня моря. Через сферичну симетрію центральних потенціалів енергія і момент моменту класичного атома водню є постійними, а орбіти обмежені лежати в площині, як планети, що обертаються навколо Сонця. Цей класичний опис механіки атома є неповним, однак, оскільки електрон, що рухається по еліптичній орбіті, прискорювався б (змінюючи напрямок) і, згідно з класичним електромагнетизмом, він повинен безперервно випромінювати електромагнітне випромінювання. Ця втрата орбітальної енергії повинна призвести до того, що орбіта електрона стає постійно меншою, поки вона не обернеться спіраллю в ядро, маючи на увазі, що атоми за своєю суттю нестабільні.

У 1913 році Нільс Бор намагався вирішити атомний парадокс, ігноруючи передбачення класичного електромагнетизму про те, що орбітальний електрон у водні буде безперервно випромінювати світло. Натомість він включив в класичну механіку опис атома Планка ідеї квантування та висновку Ейнштейна, що світло складається з фотонів, енергія яких пропорційна їх частоті. Бор припускав, що електрон, що обертається навколо ядра, зазвичай не випромінює ніякого випромінювання (гіпотеза стаціонарного стану), але він буде випромінювати або поглинати фотон, якщо він перемістився на іншу орбіту. Енергія, що поглинається або випромінюється, відображала б відмінності в орбітальних енергіях відповідно до цього рівняння:

\[ |ΔE|=|E_f−E_i|=h u=\dfrac{hc}{\lambda} \label{6.3.1} \]

У цьому рівнянні h - постійна Планка, а E _i і E _f - початкова і кінцева орбітальні енергії відповідно. Використовується абсолютне значення різниці енергій, так як частоти і довжини хвиль завжди позитивні. Замість того, щоб дозволити безперервні значення для кутового моменту, енергії та радіуса орбіти, Бор припустив, що можуть відбуватися лише дискретні значення для них (насправді квантування будь-якого з них означало б, що інші два також квантуються). Вираз Бора для квантованих енергій:

\[E_n=−\dfrac{k}{n^2} \label{6.3.2} \]

з\(n=1,2,3, ...\)

У цьому виразі\(k\) є константою, що містить фундаментальні константи, такі як маса електронів і заряд і константа Планка. Вставка виразу для енергій орбіти в рівняння для\(ΔE\) дає

\[ \color{red} ΔE=k \left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right)=\dfrac{hc}{\lambda} \label{6.3.3} \]

або

\[ \dfrac{1}{\lambda}=\dfrac{k}{hc} \left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right) \label{6.3.4} \]

Найнижчі кілька рівнів енергії показані на малюнку\(\PageIndex{1}\). Одним з фундаментальних законів фізики є те, що матерія найбільш стабільна з мінімально можливою енергією. Таким чином, електрон в атомі водню зазвичай рухається по\(n = 1\) орбіті, орбіті, на якій він має найменшу енергію. Коли електрон знаходиться на цій найнижчій енергетичній орбіті, атом, як кажуть, знаходиться в своєму наземному електронному стані (або просто наземному стані). Якщо атом отримує енергію від зовнішнього джерела, то електрон може рухатися на орбіту з більш високим\(n\) значенням і атом зараз знаходиться в збудженому електронному стані (або просто збудженому стані) з більш високою енергією. Коли електрон переходить з збудженого стану (вищої енергетичної орбіти) в менш збуджений стан, або наземний стан, різниця в енергії випромінюється у вигляді фотона. Аналогічно, якщо фотон поглинається атомом, енергія фотона переміщує електрон з нижньої енергетичної орбіти вгору на більш збуджену.

альт — Малюнок\(\PageIndex{1}\): Квантові числа та рівні енергії в атомі водню. Чим більше негативне розрахункове значення, тим нижче енергія.

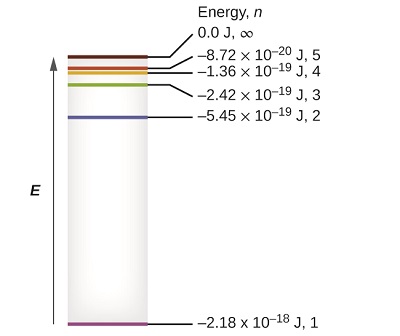
Ми можемо пов'язати енергію електронів в атомах з тим, що ми дізналися раніше про енергію. Закон збереження енергії говорить про те, що ми не можемо ні створювати, ні руйнувати енергію. Таким чином, якщо потрібна певна кількість зовнішньої енергії для збудження електрона з одного енергетичного рівня на інший, то ця ж кількість енергії буде звільнено, коли електрон повернеться в початковий стан (рис.\(\PageIndex{2}\)). По суті, атом може «зберігати» енергію, використовуючи її для просування електрона до стану з більш високою енергією і вивільнити її, коли електрон повертається в нижчий стан. Енергія може вивільнятися як один квант енергії, так як електрон повертається в свій основний стан (скажімо, від\(n = 5\) до\(n = 1\)), або вона може бути випущена як два або більше менших квантів, коли електрон падає в проміжний стан, потім в основний стан (скажімо, від\(n = 5\) до\(n = 4\), випромінюючи один квантовий, то до\(n = 1\), випромінюючи другий квант).

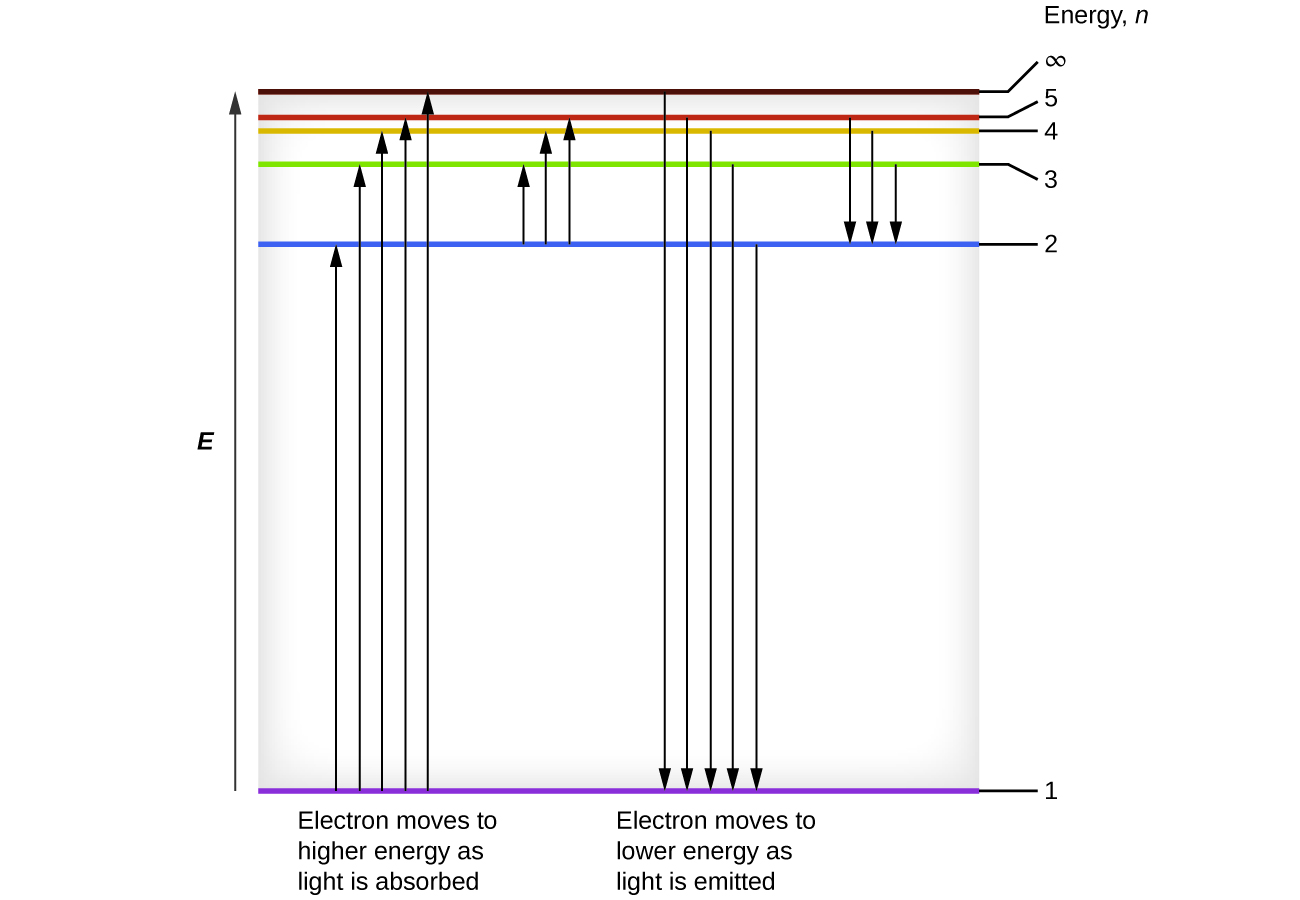
Малюнок\(\PageIndex{2}\): Горизонтальні лінії показують відносну енергію орбіт у моделі Бора атома водню, а вертикальні стрілки зображують енергію фотонів, поглинених (зліва) або випромінюваних (праворуч), коли електрони рухаються між цими орбітами.

Оскільки в моделі Бора задіяний лише один електрон, вона також може бути застосована до одиночних електронних іонів He ^⁺, Li ² ^{+, Be ³ +} тощо, які відрізняються від водню лише своїми ядерними зарядами, і тому одноелектронні атоми і іони в сукупності називають воднеподібними або гідрогенними атомами. Енергетичний вираз для воднеподібних атомів є узагальненням енергії атома водню, в якому\(Z\) є ядерний заряд (+1 для водню, +2 для He, +3 для Li і так далі) і\(k\) має значення\(2.179 \times 10^{–18}\; J\).

\[ \color{red} E_n=−\dfrac{kZ^2}{n^2} \label{6.3.5} \]

Розміри кругових орбіт для воднеподібних атомів задаються через їх радіуси наступним виразом, в якому\(a_o\) є константа, звана радіусом Бора, зі значенням\(5.292 \times 10^{−11}\; m\):

\[ \color{red} r=\dfrac{n^2}{Z} a_0 \label{6.3.6} \]

Рівняння також показує нам, що зі збільшенням енергії електрона (у міру\(n\) збільшення) електрон виявляється на більших відстанях від ядра. Це мається на увазі зворотна залежність від кулонівського потенціалу, так як\(r\) в міру віддалення електрона від ядра електростатичне тяжіння між ним і ядром зменшується, і воно утримується менш щільно в атомі. Зверніть увагу, що у міру\(n\) збільшення орбіт і збільшуються, їх енергії наближаються до нуля, і тому межі\(n⟶∞\) і\(r⟶∞\) мають на увазі, що\(E = 0\) відповідає межі іонізації, де електрон повністю видаляється з ядра. Таким чином, для водню в основному стані\(n = 1\) енергія іонізації становила б:

\[ ΔE=E_{n⟶∞} −E_1=0+k=k \label{6.3.7} \]

З трьома надзвичайно загадковими парадоксами, які зараз вирішені (випромінювання чорного тіла, фотоелектричний ефект та атом водню), і всі вони залучають постійну Планка фундаментальним чином, більшості фізиків на той час стало зрозуміло, що класичні теорії, які так добре працювали в макроскопічному світі, були принципово недосконалі і не могли бути розширені вниз в мікроскопічну область атомів і молекул. На жаль, незважаючи на чудове досягнення Бора в отриманні теоретичного виразу для постійної Рідберга, він не зміг поширити свою теорію на наступний найпростіший атом, Він, який має лише два електрони. Модель Бора була серйозно недосконалою, оскільки вона все ще базувалася на класичній механіці поняття точних орбіт, концепції, яка пізніше була визнана неспроможною в мікроскопічній області, коли була розроблена належна модель квантової механіки, щоб замінити класичну механіку.

Приклад\(\PageIndex{1}\): Calculating the Energy of an Electron in a Bohr Orbit

Ранні дослідники були дуже схвильовані, коли їм вдалося передбачити енергію електрона на певній відстані від ядра в атомі водню. Якщо іскра просуває електрон в атомі водню на орбіту з\(n = 3\), яка обчислена енергія, в джоулі, електрона?

Рішення

Енергія електрона задається рівнянням\(\ref{6.3.5}\):

\[ E=\dfrac{−kZ^2}{n^2} \nonumber \]

Атомний\(Z\) номер водню дорівнює 1\(k = 2.179 \times 10^{–18}\; J\); і електрон характеризується значенням n\(3\). Таким чином,

\[E=\dfrac{−(2.179 \times 10^{−18}\;J)×(1)^2}{(3)^2}=−2.421 \times 10^{−19}\;J \nonumber \]

Вправа\(\PageIndex{1}\)

Електрон у прикладі\(\PageIndex{1}\) в\(n=3\) державі просувається ще далі на орбіту с\(n = 6\). Яка його нова енергія?

Відповідь: ТБД

Приклад\(\PageIndex{2}\): Calculating Electron Transitions in a One–electron System

Що таке енергія (в джоулі) і довжина хвилі (в метрах) лінії в спектрі водню, що представляє рух електрона з орбіти Бора з n = 4 на орбіту з n = 6? У якій частині електромагнітного спектра ми знаходимо це випромінювання?

Рішення

В цьому випадку електрон починається з\(n = 4\), так\(n_1 = 4\). Доходить до спокою на\(n = 6\) орбіті, так що\(n_2 = 6\). Різниця в енергії між двома станами дається цим виразом:

\[ΔE=E_1−E_2=2.179 \times 10^{−18}\left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right) \nonumber \]

\[ΔE=2.179 \times 10^{−18} \left(\dfrac{1}{4^2}−\dfrac{1}{6^2}\right)\; J \nonumber \]

\[ΔE=2.179 \times 10^{−18} \left(\dfrac{1}{16}−\dfrac{1}{36}\right)\;J \nonumber \]

\[ΔE=7.566 \times 10^{−20}\;J \nonumber \]

Ця різниця енергій є позитивною, вказуючи, що фотон потрапляє в систему (поглинається) для збудження електрона від n = 4 орбіти до\(n = 6\) орбіти. Довжина хвилі фотона з цією енергією знаходить за виразом\(E=hc \lambda\). Перестановка дає:

\[ \lambda=\dfrac{hc}{E} \nonumber \]

З малюнка електромагнітного випромінювання ми бачимо, що ця довжина хвилі знаходиться в інфрачервоній частині електромагнітного спектра.

Вправа\(\PageIndex{2}\)

Яка енергія в джоулі і довжина хвилі в метрах фотона виробляється при падінні електрона\(n = 5\) з\(n = 3\) рівня в\(He^+\) іоні (\(Z = 2\)для\(He^+\))?

Відповідь: \(6.198 \times 10^{–19}\; J\)і\(3.205 \times 10^{−7}\; m\)

Модель атома водню Бора дає уявлення про поведінку речовини на мікроскопічному рівні, але вона не враховує взаємодії електрон-електронів в атомах з більш ніж одним електроном. Це вводить кілька важливих особливостей всіх моделей, що використовуються для опису розподілу електронів в атомі. До таких особливостей можна віднести наступне:

Енергії електронів (енергетичні рівні) в атомі квантуються, описуються квантовими числами: цілими числами, що мають тільки конкретне дозволене значення і використовуються для характеристики розташування електронів в атомі.
Енергія електрона збільшується зі збільшенням відстані від ядра.
Дискретні енергії (лінії) в спектрах елементів виникають з квантованих електронних енергій.

З цих особливостей найважливішим є постулат квантованих енергетичних рівнів для електрона в атомі. Як наслідок, модель заклала основу для квантової механічної моделі атома. Бор отримав Нобелівську премію з фізики за свій внесок у наше розуміння структури атомів та того, як це пов'язано з викидами лінійних спектрів.

Резюме

Бор включив ідеї квантування Планка та Ейнштейна в модель атома водню, яка вирішила парадокс стійкості атомів та дискретних спектрів. Модель Бора атома водню пояснює зв'язок між квантуванням фотонів і квантованим випромінюванням атомів. Бор описав атом водню в терміні електрона, що рухається по круговій орбіті навколо ядра. Він постулював, що електрон обмежений певними орбітами, що характеризуються дискретними енергіями. Переходи між цими дозволеними орбітами призводять до поглинання або випромінювання фотонів. Коли електрон рухається з орбіти вищої енергії на більш стабільну, енергія випромінюється у вигляді фотона. Для переміщення електрона зі стійкої орбіти на більш збуджену необхідно поглинути фотон енергії. Використовуючи модель Бора, ми можемо обчислити енергію електрона і радіус його орбіти в будь-якій одноелектронній системі.

Глосарій

Модель Бора атома водню: структурна модель, в якій електрон рухається навколо ядра тільки по кругових орбітах, кожна з яких має певний дозволений радіус; орбітальний електрон нормально не випромінює електромагнітне випромінювання, але робить це при переході з однієї орбіти на іншу.

збуджений стан: стан, що має енергію більше, ніж енергія наземного стану

земля держава: стан, в якому електрони в атомі, іоні або молекулі мають найменшу можливу енергію

квантове число: ціле число, що має тільки конкретні дозволені значення і використовується для характеристики розташування електронів в атомі