13.7: Точні розрахунки та наближення

Цілі навчання

• Зрозумійте точні рівняння, які беруть участь у складних кислотно-лужних рівновагах у водних розчині

Методи боротьби з кислотно-лужними рівновагами, які ми розробили в більш ранніх одиницях цієї серії, широко використовуються в звичайній практиці. Хоча багато з них включають наближення різного роду, результати, як правило, досить хороші для більшості цілей. Іноді, однак, наприклад, у проблемах, пов'язаних з дуже розведеними розчинами, наближення руйнуються, часто тому, що вони ігнорують малі кількості H ⁺ та OH ^- іонів, які завжди присутні в чистій воді. У цьому блоці ми розглядаємо точне, або «комплексне» лікування деяких найбільш поширених видів проблем кислотно-лужної рівноваги.

Сильні кислотно-лужні системи

Звичайне визначення «сильної» кислоти або основи - це та, яка повністю дисоціюється у водному розчині. Соляна кислота - поширений приклад сильної кислоти. Коли газ HCl розчиняється у воді, отриманий розчин містить іони H ₃ O ⁺, OH ^— і Cl ^—, але крім дуже концентрованих розчинів концентрація HCl мізерно мала; для всіх практичних цілей молекули «соляної кислоти», HCl, не існують в розведених водних розчинами. Щоб вказати концентрації трьох видів, присутніх у водному розчині HCl, нам потрібні три незалежні відносини між ними.

Обмежувальні умови

Ці відносини отримані при дотриманні того, що для водних розчинів завжди повинні дотримуватися певні умови:

1. Дисоціаційна рівновага води завжди повинна бути задоволена:\[[H^+][OH^–] = K_w \label{1-1}\]
2. Недисоційована кислота і її кон'югатна основа повинні знаходитися в балансі маси. Фактичні концентрації кислоти і її кон'югатного підстави можуть залежати від ряду факторів, але їх сума повинна бути постійною, і дорівнює «номінальній концентрації», яку ми тут позначаємо як\(C_a\). Для рішення HCl це рівняння було б\[[HCl] + [Cl^–] = C_a \label{1-2}\] Оскільки сильна кислота за визначенням повністю дисоційована, ми можемо знехтувати першим терміном і записати умову балансу маси як\[[Cl^–] = C_a \label{1-3}\]
3. У будь-якому іонному розчині сума позитивного і негативного електричних зарядів повинна дорівнювати нулю, іншими словами, всі рішення електрично нейтральні. Це відоме як принцип електронейтральності. \[[H^+] = [OH^–] + [Cl^–] \label{1-4}\]

Наступним кроком є об'єднання цих трьох граничних умов в єдиний вираз, який пов'язує концентрацію іонів гідронію\(C_a\). Це найкраще зробити, починаючи з рівняння, яке пов'язує кілька величин і підставляючи терміни, які ми хочемо усунути. Таким чином, ми можемо позбутися від\([Cl^–]\) терміна, підставивши Рівняння\(\ref{1-3}\) в Рівняння\(\ref{1-4}\):

\[[H^+] = [OH^–] + C_a \label{1-5}\]

\([OH^–]\)Термін може бути усунений за допомогою Equation\(\ref{1-1}\):

\[[H^+] = C_a + \dfrac{K_w}{[H^+]} \label{1-6}\]

Це рівняння говорить нам, що концентрація іонів гідронію буде такою ж, як і номінальна концентрація сильної кислоти, якщо розчин не дуже розбавлений. Однак, оскільки концентрація кислоти падає нижче приблизно ^10-6 М, переважає другий термін;\([H^+]\) наближається\(\sqrt{K_w}\) або\(10^{–7} M\) при 25° C. концентрація іонів гідронію, звичайно, ніколи не може опускатися нижче цього значення; жодна кількість розведення не може зробити розчин лужним!

Жодна кількість розведення не може зробити розчин сильної кислоти лужної!

Зверніть увагу, що рівняння\(\ref{1-6}\) є квадратним рівнянням; у правильному поліномі воно буде переписано як

\[[H^+]^2 – C_a[H^+] – K_w = 0 \label{1-7}\]

Більшість практичних проблем, пов'язаних з сильними кислотами, стосуються більш концентрованих розчинів, в яких другий член Рівняння\(\ref{1-7}\) може бути скинутий, даючи просте співвідношення

\[[H^+] \approx [A^–]\]

Діяльність і концентровані розчини сильних кислот

У більш концентрованих розчинів взаємодії між іонами змушують їх «ефективні» концентрації, відомі як їх діяльність, відхилятися від їх «аналітичних» концентрацій. Таким чином, в розчині, приготованому шляхом додавання 0,5 моль дуже сильної кислоти HClO ₄ до достатньої кількості води, щоб зробити обсяг 1 літр, вимірювання температури замерзання депресії показують, що концентрації іонів гідронію і перхлорату становлять всього близько 0,4 М. Це не означає, що кислота дисоційована лише на 80%; немає доказів молекул HClO ₄ в розчині. Що сталося, так це те, що близько 20% іонів H ₃ O ⁺ і ClO ₄ ^— утворили іонно-парні комплекси, в яких протилежно заряджені види вільно пов'язані електростатичними силами. Аналогічно в 0,10 М розчині соляної кислоти активність Н ⁺ становить 0,81, або всього 81% від її концентрації. (Дивіться зелене поле нижче, щоб дізнатися більше про це.)

Діяльність важлива, оскільки тільки вони працюють належним чином в рівноважних розрахунках. Зв'язок між концентрацією виду і його активністю виражається коефіцієнтом активності\(\gamma\):

\[a = \gamma C \label{1-8}\]

У міру того як розчин стає більш розбавленим,\(\gamma\) наближається єдність. При іонних концентраціях нижче приблизно 0,001 М концентрації, як правило, можуть використовуватися замість діяльності з незначною похибкою. Нагадаємо, що рН визначається як негативний логарифм активності іонів водню, а не його концентрації.

Діяльність одиночних іонів неможливо визначити, тому коефіцієнти активності в іонних розчинях завжди є середніми або середніми показниками для всіх іонних видів, присутніх. Ця величина позначається як\(\gamma_{\pm}\).

При дуже високих концентраціях діяльність може дико відходити від концентрацій. Це практичне міркування при роботі з сильними мінеральними кислотами, які доступні в концентраціях 10 М або більше. У 12 М розчині соляної кислоти, наприклад, середній коефіцієнт іонної активності* дорівнює 207. Це означає, що в цих умовах з [H ⁺] = 12 активність {H ⁺} = 2500, що відповідає рН близько —3,4, замість —1,1, як можна було б передбачити, якщо концентрації використовувалися. Ці дуже високі коефіцієнти активності також пояснюють інше явище: чому ви можете виявити запах HCl над концентрованим розчином соляної кислоти, навіть якщо ця кислота нібито "100% дисоційована».

При цих високих концентраціях пара «дисоційованих» іонів\(H^+\) іноді виявляються настільки близько один до одного, що вони можуть на\(Cl^–\) мить діяти як одиниця HCl; деякі з них можуть втекти, як до\(HCl(g)\) того, як теплові рухи знову розбивають їх. У цих умовах «дисоціація» починає втрачати свій сенс так, що по суті дисоціація вже не є повною. Хоча концентрація завжди\(HCl(aq)\) буде дуже маленькою, його власний коефіцієнт активності може бути таким же великим, як 2000, а це означає, що його тенденція виходу з розчину надзвичайно висока, так що наявність навіть крихітної кількості дуже помітна.

Слабкі монопротонові кислоти і основи

Більшість кислот слабкі, їх сотні тисяч, тоді як сильних кислот не більше декількох десятків. Ми можемо лікувати слабкі кислотні розчини точно так само, як і для сильних кислот. Єдина відмінність полягає в тому, що тепер ми повинні включити вираз рівноваги для кислоти. Почнемо з простого випадку чистої кислоти у воді, а потім перейдемо звідти до більш загального, в якому присутні сильні катіони. У цій експозиції ми будемо посилатися на «іони водню» і\([H^+]\) для стислості, і будемо вважати, що кислота\(HA\) дисоціює\(H^+\) і її кон'югатну основу\(A^-\).

Чиста кислота у воді

На додаток до видів H ⁺, OH ^- і A - які ми мали в сильнокислотному випадку, тепер у нас є недисоційована кислота HA; чотири змінні, що вимагають чотирьох рівнянь.

• Рівноваги

\[ [H^+][OH^–] = K_w \label{2-1}\]

\[ K_a = \dfrac{[H^+][A^–]}{[HA]} \label{2-2}\]

• Баланс маси

\[ C_a = [HA] + [A^–] \label{2-3}\]

• Баланс заряду

\[[H^+] = [OH^–] + [HA^–] \label{2-4}\]

Щоб виключити [HA] з Рівняння\(\ref{2-2}\), вирішимо рівняння\(\ref{2-4}\) для цього члена і підставляємо отриманий вираз в чисельник:

\[ K_a =\dfrac{[H^+]([H^+] - [OH^-])}{C_a-([H^+] - [OH^-]) } \label{2-5}\]

Останнє рівняння спрощується множенням і заміною [H ⁺] [OH ^—] на K _w. Потім ми позбавляємося від [ОН ^—] термін, замінивши його на K _w/[H ⁺]

\[[H^+] C_b + [H^+]^2 – [H^+][OH^–] = K_a C_a – K_a [H^+] + K_a [OH^–]\]

\[[H^+]^2 C_b + [H^+]^3 – [H^+] K_w = K_a C_a – K_a [H^+] + \dfrac{K_a K_w}{[H^+]}\]

Переставляється в стандартну многочленную форму, це стає

\[[H^+]^3 + K_a[H^+]^2 – (K_w + C_aK_a) [H^+] – K_a K_w = 0 \label{2-5a}\]

Для більшості практичних застосувань ми можемо зробити наближення, які усувають необхідність розв'язання кубічного рівняння.

Наближення 1: Нехтування популяції гідроксиду

Якщо кислота не є надзвичайно слабкою або розчин дуже розбавлений, концентрацією ОН ^- можна знехтувати порівняно з концентрацією [Н ⁺]. Якщо припустити, що [OH ^—] [H ⁺], то рівняння\(\ref{2-5a}\) можна спростити до

\[K_a \approx \dfrac{[H^+]^2}{C_a-[H^+]} \label{2-6}\]

що являє собою квадратне рівняння:

\[[H^+]^2 +K_a[H^+]– K_aC_a \approx 0 \label{2-7}\]

і, таким чином, з квадратичної формули,

\[ [H^+] \approx \dfrac{K_a + \sqrt{K_a + 4K_aC_a}}{2} \label{2-8}\]

Приклад\(\PageIndex{1}\): Acetic Acid

Розрахувати рН 0,0010 М розчину оцтової кислоти,\(K_a = 1.74 \times 10^{–5}\).

Рішення

Перше наближення:

\[[H^+] = \sqrt{(1.0 \times 10^{–3}) × (1.74 \times 10^{–5}} = \sqrt{1.74 \times 10^{–8}} = 1.3 \times 10^{–4}\; M. \nonumber \]

Застосовуючи "5% тест»,

\[\dfrac{1.3 \times 10^{–4}}{1.0 \times 10^{–3}} = 0.13\nonumber \]

Це перевищує 0,05, тому ми повинні явно вирішити квадратне рівняння,\(\ref{2-7}\) щоб отримати два\(+1.2 \times 10^{–4}\) корені: і\(–1.4 \times 10^{-4}\). Беручи позитивний корінь, ми маємо

\[pH = –\log (1.2 \times 10^{–4}) = 3.9 \nonumber \]

Наближення 2: Дуже концентровані кислоти

Якщо кислота досить концентрована (зазвичай більше 10 ^—3 М), подальше спрощення часто можна досягти, зробивши припущення, що\([H^+] \ll C_a\). Це виправдано, коли більша частина кислоти залишається в протонованій формі [HA], так що виробляється відносно мало Н ⁺. У цьому випадку рівняння\(\ref{2-6}\) зводиться до

\[ K_a \approx \dfrac{[H^+]^2}{C_a} \label{2-9}\]

або

\[[H^+] \approx \sqrt{K_aC_a} \label{2-10}\]

Приклад\(\PageIndex{2}\)

Розрахувати рН і відсоток іонізації 0,10 М оцтової кислоти «HaC» (СН ₃ СООН),\(K_a = 1.74 \times 10^{–5}\).

Рішення:

Зазвичай найкраще почати з використання Equation\(\ref{2-9}\) як першого наближення:

\[[H^+] = \sqrt{(0.10)(1.74 \times 10^{–5})} = \sqrt{1.74 \times 10^{–6}} = 1.3 \times 10^{–3}\; M\nonumber \]

Це наближення, як правило, вважається дійсним, якщо [H ⁺] менше 5% від C _a; в цьому випадку [H ⁺] /C _a = 0,013, що менше 0,05 і, отже, в межах межі. Ця ж величина також відповідає частці іонізації, тому відсоток іонізації становить 1,3%. Показник рН розчину становить

\[pH = –\log 1.2 \times 10^{-3} = 2.9\nonumber \]

Наближення 3: Дуже слабкий і кислий

Якщо кислота дуже слабка або її концентрація дуже низька,\(H^+\) вироблена її дисоціацією може бути трохи більше, ніж через іонізацію води. Однак, якщо розчин все ще кислий, все одно можна уникнути вирішення кубічного рівняння,\(\ref{2-5a}\) припустивши, що термін\(([H^+] - [OH^–]) \ll C_a\) у рівнянні\(\ref{2-5}\):

\[ K_a = \dfrac{[H^+]^2}{C_a - [H^+]} \label{2-11}\]

Це можна переставити в стандартну квадратичну форму

\[[H^+]^2 + K_a [H^+] – K_a C_a = 0 \label{2-12}\]

Для розведених розчинів слабких кислот може знадобитися точна обробка. За допомогою комп'ютера або графічного калькулятора рішення кубічного полінома тепер набагато менш грізно, ніж раніше. Однак помилки округлення можуть призвести до того, що ці комп'ютеризовані кубічні розв'язувачі підірвуться; як правило, безпечніше використовувати квадратичне наближення.

Приклад\(\PageIndex{3}\): Boric Acid

Борна кислота, В (ОН) ₃ («Н _{3 БО 3} «) - слабка кислота, що міститься в океані і в деяких природних водах. Як і у багатьох сполук бору, виникає певне питання про його справжню природу, але для більшості практичних цілей його можна вважати монопротическим при\(K_a = 7.3 \times 10^{–10}\):

\[Bi(OH)_3 + 2 H_2O \rightleftharpoons Bi(OH)_4^– + H_3O^+\nonumber \]

Знайдіть [Н ⁺] і рН 0,00050 М розчину борної кислоти в чистій воді.

Рішення

Оскільки ця кислота досить слабка, а її концентрація низька, ми будемо використовувати квадратичну форму Рівняння\(\ref{2-7}\), яка дає позитивний корінь\(6.12 \times 10^{–7}\), відповідний рН = 6,21. Зверніть увагу, що це лише в шість разів перевищує концентрацію\(H^+\) присутніх у чистій воді!

Повчально порівнювати цей результат з тим, що дасть квадратичне наближення, яке дає\([H^+] = 6.04 \times 10^{–7}\) так\(pH = 6.22\).

слабкі підстави

Найбільш часто зустрічаються слабкі підстави:

• аніони А ^— слабких кислот:

\[A^– + H_2O \rightleftharpoons HA + OH^–\]

\[CO_3^{2–} + H_2O \rightleftharpoons HCO_3^– + OH^–\]

• нашатирний спирт

\[NH_3 + H_2O \rightleftharpoons NH_4^+ + OH^–\]

• аміни, наприклад метиламін

\[CH_3NH_2 + H_2O \rightleftharpoons CH_3NH_3^++ H_2O\]

Розчин аніона слабкої кислоти

Відзначимо, що для підтримки електронейтральності аніони повинні супроводжуватися достатньою кількістю катіонів, щоб збалансувати свої заряди. Таким чином, для C _b M розчину солі NaA у воді ми маємо наступні умови:

• Види

Na ⁺, А ^—, ГА, Н ₂ О, Н ⁺, О ^—

• Рівноваги

\[[H^+][OH^–] = K_w \label{2-13}\]

\[ K_b =\dfrac{[HA][OH^-]}{[A^-]} \label{2-14}\]

• Баланс маси

\[C_b = [Na^+] = [HA] + [A^–] \label{2-15}\]

• Баланс заряду

\[[Na^+] + [H^+] = [OH^–] + [A^–] \label{2-16}\]

\(\ref{2-15}\)Замінюючи термін [Na ⁺] в Рівнянні\(C_b\)\(K_w\) і поєднуючи з і баланс маси, виходить відношення, аналогічне рівнянню\(\ref{2-5}\) для слабких кислот:

\[K_b =\dfrac{[OH^-] ([OH^-] - [H^+])}{C_b - ([OH^-] - [H^+])} \label{2-17}\]

наближення

\[ K_b \approx \dfrac{[OH^-]^2}{C_b - [OH^-]} \label{2-18}\]

і

\[[OH^–] \approx \sqrt{K_b C_b} \label{2-19}\]

можуть бути виведені аналогічним чином.

Приклад\(\PageIndex{4}\): Methylamine

Обчисліть рН і концентрації всіх видів в 0,01 М розчині метиламіну, CH ₃ NH ₂ (\(K_b = 4.2 \times 10^{–4}\)).

Рішення

Почнемо з використання найпростішого рівняння наближення\(\ref{2-14}\):

\[[OH^–] = \sqrt{(K_b C_b}- = \sqrt{(4.2 \times 10^{-4})(10^{–2})} = 2.1 \times 10^{–3}\nonumber \]

Щоб побачити, чи виправдано це наближення, ми застосуємо критерій, подібний до того, що ми використовували для слабкої кислоти: [ОН ^—] не повинен перевищувати 5% C _b. У цьому випадку

\[ \dfrac{[OH^–]}{ C_b} = \dfrac{(2.1 \times 10^{-3}} { 10^{–2}} = 0.21\nonumber \]

тому ми повинні використовувати квадратичну форму Рівняння\(\ref{2-12}\), що дає позитивний корінь\(1.9 \times 10^{–3}\), який відповідає\([OH^–]\)

\[[H^+] = \dfrac{K_w}{[OH^–} = \dfrac{1 \times 10^{-14}}{1.9 \times 10^{–3}} = 5.3 \times 10^{-12}\nonumber \]

і

\[pH = –\log 5.3 \times 10^{–12} = 11.3.\nonumber \]

З рівняння балансу заряду вирішуємо для

\[[CH_3NH_2] = [OH^–] – [H^+] \approx [OH^–] = 5.3 \times 10^{–12}\; M. \nonumber \]

Для концентрації кислотної форми (іон метиламінію CH ₃ NH ₃ ⁺) використовують рівняння балансу маси:

\[[CH_3NH_3^+] = C_b – [CH_3NH_2] = 0.01 – 0.0019 =0.0081\; M.\nonumber \]

Суміші кислот

Багато практичні проблеми, що стосуються екологічної та фізіологічної хімії, пов'язані з розчинами, що містять більше однієї кислоти. У цьому розділі ми обмежимося набагато простішим випадком двох кислот, з метою показати загальний метод наближення до таких задач, починаючи з рівнянь заряду та маси та роблячи спрощені припущення, коли це виправдано. Загалом, іони водню, що виробляються сильнішою кислотою, будуть, як правило, пригнічувати дисоціацію слабшого, і обидва будуть схильні до придушення дисоціації води, тим самим зменшуючи джерела Н ⁺, з якими потрібно боротися.

Розглянемо суміш двох слабких кислот HX і HY; їх відповідні номінальні концентрації і константи рівноваги позначаються C _x, C _y, K _x і K _y,

Починаючи з вираження балансу заряду

\[ [H^+] = [X^–] + [Y^–] + [OH^–] \label{3-1}\]

Ми використовуємо константи рівноваги для заміни сполучених базових концентрацій виразами виду

\[ [X^-] = K_x \dfrac{[HX]}{[H^+]} \label{3-2}\]

поступитися

\[ [H^+] = \dfrac{[HX]}{K_x} + \dfrac{[HY]}{K_y} + K_w \label{3-3}\]

Якщо жодна кислота не є дуже сильною або дуже розбавленою, ми можемо замінити рівноважні концентрації номінальними концентраціями:

\[ [H^+] \approx \sqrt{C_cK_x + C_yK_y K_w} \label{3-4}\]

Приклад\(\PageIndex{5}\): Acetic Acid and Formic Acid

Оцініть рН розчину, який становить 0,10 М в оцтовій кислоті (\(K_a = 1.8 \times 10^{–5}\)) і 0,01 М в мурашиній кислоті (\(K_a = 1.7 \times 10^{–4}\)).

Рішення

Оскільки K _w є незначним порівняно з виробами C _a K _a, ми можемо спростити\ Рівняння\(ref{3-4}\):

\[[H^+] = \sqrt{1.8 \times 10^{–6} + 1.7 \times 10^{-6}} = 0.0019\nonumber \]

Що відповідає рН\(–\log 0.0019 = 2.7\)

Зверніть увагу, що рН кожної кислоти окремо при зазначеній концентрації буде близько 2,8. Однак якщо замість мурашиної кислоти використовується 0,001 М хлороцтової кислоти (K _a = 0,0014), вищевказаний вираз стає

\[ [H^+] \approx \sqrt{ 1.4 \times 10^{-6} + 1.75 \times 10^{-14}} = 0.00188 \label{3-5}\]

яка перевищує концентрацію сильнішої кислоти; оскільки оцтова кислота робить незначний внесок у [H ⁺] тут, просте наближення, наведене вище\ Рівняння, явно\(\ref{3-3}\) недійсне. Тепер ми використовуємо вираз балансу маси для сильнішої кислоти

\[[HX] + [X^–] = C_x \label{3-6}\]

розв'язати для [X ^—], який поєднується з постійною рівноваги K _x до виходу

\[[X^-] = C_x - \dfrac{[H^+][X^]}{K_x} \label{3-7}\]

Рішення цього для [X ^—] дає

\[ [X^-] = \dfrac{C_xK_x}{K_x + [H^+]} \label{3-8}\]

Наближення для слабшої оцтової кислоти (HY) все ще діє, тому ми зберігаємо її в заміщеному вираженні електронегативності:

\[ [H^+] \dfrac{C_xK_x}{K_x+[H^+]} + \dfrac{C_yK_y}{[H^+]} \label{3-9}\]

що являє собою кубічне рівняння, яке можна вирішити шляхом наближення.

Опубліковано кілька методів розрахунку концентрації іонів водню в розчині, що містять довільну кількість кислот і підстав. Вони, як правило, передбачають ітераційні обчислення, що проводяться комп'ютером. Див., наприклад, Дж. Освіта 67 (6) 501-503 (1990) та 67 (12) 1036-1037 (1990).

Рівноваги поліпротових кислот

Завдяки великій кількості задіяних видів точні рішення проблем, пов'язаних з поліпротовими кислотами, можуть стати дуже складними. Таким чином, для фосфорної кислоти H ₃ PO ₄ три стадії «дисоціації» дають три кон'югатні основи:

На щастя, зазвичай можна зробити спрощуючі припущення в більшості практичних застосувань. У наступному розділі ми покажемо, як це робиться для менш складного випадку дипротової кислоти. ГК дипротової кислоти може здавати свої протони в два етапи, отримуючи спочатку монопротонований вид HA ^- а потім повністю депротоновану форму A ^2—.

Оскільки існує п'ять невідомих (концентрації кислоти, двох сполучених основ і H ⁺ і OH ^-), нам потрібно п'ять рівнянь, щоб визначити співвідношення між цими величинами. Такими є

• Рівноваги

\[[H^+][OH^–] = K_w \label{4-1}\]

\[ K_1 = \dfrac{[H^+][HA^-]}{[H_2A]} \label{4-2}\]

\[ K_1 = \dfrac{[H^+][HA^{2-}]}{[HA^-]} \label{4-3}\]

• Баланс маси

\[C_a = [H_2A] + [HA^–] + [A^{2–}] \label{4-4}\]

• Баланс заряду

\[[H^+] = [OH^–] + [HA^–] + 2 [A^{2–}] \label{4-5}\]

(Потрібно 2 молі,\(H^+\) щоб збалансувати заряд 1 моль\(A^{2–}\))

Розв'язування цих п'яти рівнянь одночасно для\(K_1\) дає досить страхітливий вираз

\[ K_1 = \dfrac{[H^+] \left( [H^+] - [OH^-] \dfrac{2K_2[H^+] - [OH^-]}{[H^+ + 2K_2} \right)}{C_a - \left( [H^+] - [OH^-] \dfrac{K_2 [H^+] -[OH^-]}{[H^+] + 2K_2} \right)} \label{4-6}\]

що мало практичного використання, за винятком випадків, коли він забезпечує відправну точку для різних спрощуючих наближень.

Якщо розчин навіть слабокислий, то ([Н ⁺] — [ОН ^—]) ≈ [Н ⁺] і

\[ K_1 = \dfrac{[H^+] \left( [H^+] \dfrac{2K_2[H^+]}{[H^+ + 2K_2} \right)}{C_a - \left( [H^+] \dfrac{K_2 [H^+]}{[H^+] + 2K_2} \right)} \label{4-7}\]

Для будь-якої з поширених дипротових кислот,\(K_2\) набагато менше, ніж\(K_1\). Якщо розчин досить кислий\(K_2 \ll [H^+]\), то можна зробити подальше спрощення, яке видаляє\(K_2\) з Рівняння\(\ref{4-7}\); це відправна точка для більшості практичних розрахунків.

\[ K_1 \approx \dfrac{[H^+]^2}{C_a-[H^+]} \label{4-8}\]

Нарешті, якщо розчин досить концентрований і\(K_1\) досить малий\([H^+] \ll C_a\), щоб, то Рівняння\(\ref{4-8}\) зводиться до:

\[ [H^+] \approx \sqrt{K_a C_a}\]

Кислота з кон'югатною основою: Буферні розчини

Розчини, що містять слабку кислоту разом з сіллю кислоти, в сукупності відомі як буфери. Коли вони використовуються для контролю рН розчину (наприклад, у середовищі для росту мікробів), зазвичай використовується натрієва або калієва сіль, і концентрації, як правило, досить високі, щоб рівняння Гендерсона-Хассельбальха дало адекватні результати.

Точне рішення

У цьому розділі ми розробимо точну аналітичну обробку слабких кислотно-сольових розчинів і покажемо, як виникає рівняння Н ^— Н як наближення. Типова буферна система утворюється шляхом додавання до розчину слабкої кислоти ГК кількості міцної основи, такої як гідроксид натрію. Як варіант, ту ж систему можна зробити, поєднуючи відповідні кількості слабкої кислоти і її солі NaA. Систему такого роду можна обробляти практично так само, як і слабку кислоту, але тепер з параметром C _b на додаток до С _а.

• Види

Na ⁺, А ^—, ГА, Н ₂ О, Н ⁺, О ^—

• Рівноваги

\[[H^+][OH^–] = K_w \label{5-1}\]

\[K_a = \dfrac{[H^+][A^-]}{[HA]} \label{5-2}\]

• Баланс маси

\[C_a + C-b = [HA] + [A^–] \label{5-3}\]

\[C_b = [Na^+] \label{5-4}\]

• Баланс заряду

\[[Na^+] + [H^+] = [OH^–] + [A^–] \label{5-5}\]

Підстановка рівняння\(\ref{5-4}\) в рівняння\(\ref{5-5}\) дає вираз для [A ^—]:

\[[A^–] = C_b + [H^+] – [OH^–] \label{5-6}\]

Вставка цього в рівняння\(\ref{5-3}\) та рішення для [HA] врожайності

\[[HA] = C_b + [H^+] – [OH^–] \label{5-7)}\]

Нарешті, ми підставляємо ці два останні вирази в константу рівноваги (Equation\(\ref{5-2}\)):

\[ [H^+] = K_a \dfrac{C_a - [H^+] + [OH^-]}{C_b + [H^+] - [OH^-]} \label{5-8}\]

який стає кубічним у [H ⁺], коли [OH ^—] замінюється на (K _w/[H ⁺]).

\[[H^+]^3 +(C_b +K_a)[H^+]^2 – (K_w + C_aK_a) [H^+] – K_aK_w = 0 \label{5-8a}\]

наближення

Практично у всіх практичних випадках можна зробити спрощуючі припущення. Таким чином, якщо розчин, як відомо, є кислим або лужним, то термінами [ОН ^—] або [Н ⁺] в Рівнянні\(\ref{5-8}\) можна знехтувати. У кислих розчині, наприклад, Рівняння\(\ref{5-8}\) стає

\[ [H^+] = K_a \dfrac{C_a - [H^+]}{C_b + [H^+]} \label{5-9}\]

які можуть бути перебудовані в квадратичну в стандартній многочленной формі:

\[ [H^+]^2 + (C_b + C_a)  [H^+] – K_a C_a = 0 \label{5-10}\]

Якщо концентрації C _a і C _b досить великі, можливо, можна знехтувати термінами [H ⁺] повністю, що призводить до поширеного наближення Гендерсона-Хассельбальха.

\[ \color{red} [H^+] \approx K_a \dfrac{C_a}{C_b} \label{5-11}\]

Важливо мати на увазі, що наближення Гендерсона-Хассельбальха - це «наближення наближення», яке, як правило, справедливо лише для комбінацій K _a та концентрацій, які потрапляють у кольорову частину цієї ділянки.

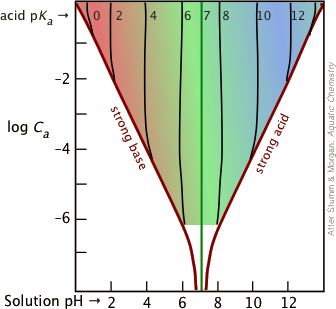
Більшість буферних розчинів, як правило, досить концентровані, причому C _a і C _b зазвичай близько 0,01 - 0,1 М. Для більшої кількості розбавлених буферів і більших K _a, які приведуть вас до межі кольорової області, безпечніше почати з Equation\(\ref{5-9}\).

Приклад\(\PageIndex{6}\): Chlorous Acid Buffer

Хлорноватиста кислота HClO _{2 має} рК а 1,94. Розрахунок рН розчину проводиться шляхом додавання 0,01 М/л гідроксиду натрію в -0,02 М/л розчину хлорної кислоти.

Рішення

В отриманому розчині С _а = С _б = 0,01 М. На зображених вище ділянках перетин лінії колоди C _a = —2 з ділянкою для pK _a = 2 припадає біля лівої межі кольорового ділянки, тому будемо використовувати квадратичну форму\(\ref{5-10}\).

Заміна у виході\(\ref{5-10}\) рівняння

\[H^+ + 0.02 H^+ – (10^{–1.9} x 10^{–2}) = 0 \nonumber\]

який дає позитивний корінь 0,0047 = [H ⁺], що відповідає рН = 2,3.

Примітка: Використання наближення Гендерсона-Хассальбаха (рівняння\(\ref{5-11}\)) дасть рН = pK _a = 1.9.