13.4: Сполучених пар та буферів

Цілі навчання

Переконайтеся, що ви добре розумієте наступні основні поняття:

• Створіть значення C _a і C _b після того, як слабка монопротова кислота або основа були частково нейтралізовані сильною основою або кислотою.
• Визначте частку іонізації та розрахуйте відсоток іонізації C _A M розчину слабкої монопротової кислоти.
• Намалюйте приблизний сюжет, що показує розподіл сполучених видів у розчині слабкої кислоти, що має задане значення K _a.
• Визначте буферний розчин та поясніть, як він працює.
• Обчисліть приблизний рН розчину слабкої монопротової кислоти, що _{має заданий рК а}, який був частково нейтралізований додаванням міцної основи.
• Вкажіть, як зробити заданий обсяг буферного розчину, що має певний рН, починаючи зі слабкої кислоти і гідроксиду натрію.
• Визначте буферний індекс і поясніть його значення і умови, за яких його величина максимізується.
• Намалюйте графік —log C vs pH (Sillén) для слабкої системи монопротної кислоти/основи, що має задану номінальну концентрацію та pK _a, і використовувати його для оцінки рН розчину.

Ми часто схильні розглядати рН як величину, яка залежить від інших змінних, таких як концентрація та сила кислоти, основи або солі. Але в більшій частині хімії (і особливо в біохімії) ми вважаємо більш корисним розглядати рН як «головну» змінну, яка контролює відносні концентрації кислотно-базових форм одного або декількох наборів кон'югатних кислотно-лужних систем. У цьому уроці ми розглянемо цей підхід досить докладно, показавши його застосування до самих практичних тем буферних розчинів, а також використання простого графічного підходу, який дозволить оцінити рН слабкої монопротной або поліпротової кислоти або основи, не роблячи взагалі ніякої арифметики!

Коли рН бере під контроль

Якщо додати 0,2 моль гідроксиду натрію до розчину, що містить 1,0 моль слабкої кислоти ГК, то еквівалентна кількість молів цієї кислоти буде перетворено в її базову форму А ^—. Отриманий розчин буде містити 0,2 моль А ^— і 0,8 моль ГК. Зауважимо, що оскільки ми обговорюємо стехіометрію тут, нас цікавлять кількості (молі) реагентів, а не концентрації реагентів.

Важливим моментом, який слід розуміти, є те, що ми отримаємо «частково нейтралізований» розчин, в якому і кислота, і її кон'югатна основа присутні у значних кількостях. Розчини такого роду зустрічаються набагато частіше, ніж чиста кислота або чиста основа, і дуже важливо, щоб ви мали глибоке розуміння їх.

Приклад\(\PageIndex{1}\): Partly neutralized acid

До розчину, що містить 0,010 моль оцтової кислоти (HaC), додаємо 0,002 моль гідроксиду натрію. Якщо обсяг кінцевого розчину дорівнює 100 мл, знайдіть значення С _а, С _b, і загальну системну концентрацію C _t.

Рішення

Доданий гідроксид-іон, будучи сильною основою, повністю реагує з оцтовою кислотою, залишаючи 0,010-0,002 = 0,008 моль HaC і 0,002 моль ацетатного іона Ac ^—. Кінцеві концентрації

\[C_a = \dfrac{0.008 \;mol}{0.10\; L} = 0.08 \; M\]

\[C_b = \dfrac{0.002 \; mol}{ 0.10 \; L} = 0.02 M\]

\[Ct = \dfrac{0.010 \;mol}{0.10\; L} = 0.10\; M.\]

Врахуйте, що цей розчин був би невідмінним від одного, приготованого шляхом _{поєднання С а} = 0,080 моль оцтової кислоти з С _b = 0,020 моль ацетату натрію і регулювання обсягу до 100 мл.

Таким чином, починаючи з розчину чистої слабкої кислоти або слабкої основи у воді, ми можемо додати достатню сильну основу або сильну кислоту, відповідно, для регулювання співвідношення кон'югатних видів — тобто співвідношення [ГА]/[А ^—] у випадку кислоти, або [B]/[BH ⁺] для основи, до будь-якого значення, яке ми хочемо.

Фракції іонізації

Для вираження відносних концентрацій протонованих та депротонованих форм кислотно-лужної системи, присутніх у розчині, ми могли б використовувати просте співвідношення [HA]/[A] (або його зворотне), але це страждає від недоліку отримання невизначеного результату, коли концентрація в знаменнику дорівнює нулю. Для багатьох цілей зручніше використовувати фракції іонізації.

\[\alpha_0 = \dfrac{[HA]}{[HA]+A^-]} = \dfrac{[HA]}{C_a} \label{1-7a}\]

\[\alpha_1 = \dfrac{[A^-]}{[HA]+A^-]} = \dfrac{[A^-]}{C_a} \label{1-7b}\]

\(\alpha_1\)Фракція також відома як ступінь дисоціації кислоти. Здійснюючи відповідні заміни, використовуючи відношення

\[[H^+] = K_a \dfrac{[HA]}{[A^-]} \label{1-8}\]

ми можемо висловити фракції іонізації як функції рН:

\[\alpha_0 = \dfrac{[H^+]}{K_a+[H^+]} \label{1-9a}\]

\[\alpha_1 = \dfrac{K_a}{K_a+[H^+]} \label{1-9b}\]

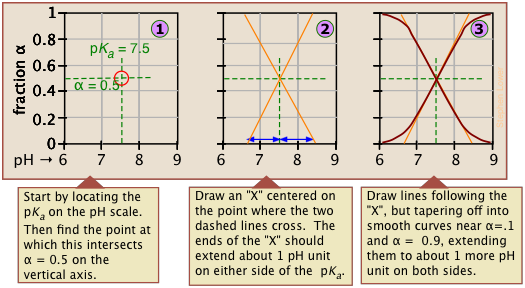
Зверніть увагу, що значення для обох цих функцій близькі до нуля або одиниці, за винятком діапазону рН pK _a ± 1 (рис.\(\PageIndex{1}\)).

Малюнок\(\PageIndex{1}\): Часткова іонізація слабкої кислоти

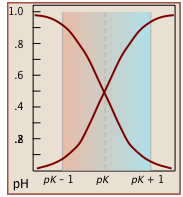
Графіки\(\alpha\) функцій vs. pH для декількох систем наведені нижче. Зверніть увагу на точки перетину, де [HA] = [A] коли [H ⁺] = K _a, що відповідає одиничному значенню частки в наближенні Гендерсона-Хассельбальха.

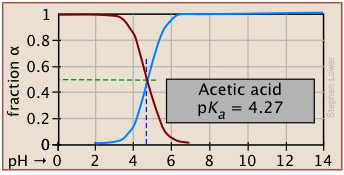
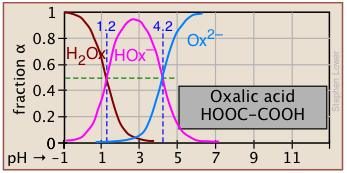
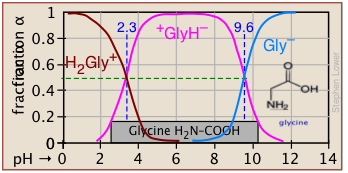
Фракції іонізації серії кислот у широкому діапазоні рН можна зручно узагальнити, як показано нижче.

Малюнок\(\PageIndex{2}\): Фракції іонізації ряду кислот

Якщо ви знаєте pK _а кислоти, ви можете легко накидати його ділянку фракції іонізації. Крайні вершини та днища можна оцінити лише, але решта ділянок - це по суті прямі лінії.

Настільки цінні, як ці ділянки для того, щоб показати, як розподіл сполучених видів змінюється залежно від рН, вони страждають від двох недоліків:

• Графіки\(\alpha\) охоплюють лише один порядок, але фактичні концентрації, які нас часто більше цікавлять, варіюються в набагато більшому діапазоні від pH 0 до 14.
• Вони мало допомагають, якщо хтось хоче оцінити рН розчину кислоти або основи, або однієї з її солей.

Обидва ці обмеження легко подолані за допомогою легко побудованих логарифмічних ділянок, які ми описуємо в наступному розділі.

Буферні розчини

Слово буфер має кілька значень англійською мовою, більшість з них посилаються (у своїй дієслівній формі) на подушку, захист, захист або протидію несприятливому ефекту. У хімії це стосується конкретно розчину, який протистоїть зміні рН при додаванні кислоти або основи. Буферний (або буферний) розчин - це той, який протистоїть зміні його рН, коли H ⁺ або OH ^- іони додаються або видаляються внаслідок якоїсь іншої реакції, що відбувається в тому ж розчині. Буферні розчини є необхідними компонентами всіх живих організмів.

• Наша кров буферується для підтримки рН 7,4, який повинен залишатися незмінним, оскільки метаболічно генерується CO ₂ (вугільна кислота) додається, а потім видаляється нашими легенями.
• Буфери в океанах, у природних водах, таких як озера та струмки, та всередині ґрунтів допомагають підтримувати їх екологічну стабільність проти кислотних дощів та збільшення атмосферного CO ₂.
• Багато промислових процесів, таких як пивоваріння, вимагають контролю буфера, як і дослідження біохімії та фізіології, які включають ферменти, активні лише в певних діапазонах рН.

Істотним компонентом буферної системи є кон'югатна кислотно-лужна пара, концентрація якої досить висока по відношенню до концентрацій доданих H ⁺ або OH ^- очікується, що вона буферна проти. Проста буферна система може бути 0,2 М розчин ацетату натрію; кон'югатна пара тут - оцтова кислота HaC та її кон'югатна основа, ацетатний іон Ac ^-. Ідея полягає в тому, що ця сполучена пара «пул» буде доступна для зжерти будь-яке невелике (≤ 10 ^—3 M) додавання H+ або OH ^- що може бути результатом інших процесів, що відбуваються в розчині.

Малюнок\(\PageIndex{1}\): Буфер

Вправа\(\PageIndex{1}\)

Намалюйте подібну діаграму, яка показує, що відбувається, коли ви видаляєте H ⁺ або OH ^-.

Відповідь

Коли це станеться, співвідношення [haC]/[Ac ^—], залишиться істотно незмінним, як і рН, як ви побачите нижче.

Ви також можете подумати про процес, зображений вище, з точки зору принципу Ле Шательє: додавання H ⁺ до розчину пригнічує дисоціацію HaC, частково протидіючи ефекту доданої кислоти, як показано рівнянням в лівому нижньому куті наведеної діаграми.

Наближення Гендерсона-Хассельбальха

Щоб розвинути це більш кількісно, ми розглянемо загальний випадок слабкої кислоти ГК, до якої додано кількість C _b міцної основи; подумайте, наприклад, про оцтову кислоту, яка була частково нейтралізована гідроксидом натрію, отримуючи ту ж кон'югатну пару, описану вище, хоча і не обов'язково однакові концентрації. Баланс маси для такої системи був би

\[[HA] + [A^–] = C_a + C_b = C_T \label {2-1}\]

в якому С _т позначає загальну концентрацію всіх видів в розчині. Оскільки до кислоти ми додали сильну (повністю дисоційовану) основу NaOH, ми також відзначимо, що

\[C_b = [Na^+] \label{2-2}\]

Згадуючи вираз рівноваги для слабкої кислоти

\[K_a = \dfrac{[H^+][A^-]}{[HA]} \label{2-3}\]

Ми можемо вирішити це для [H ⁺]:

\[[H^+] = K_a \dfrac{[HA]}{[A^-]} \label{2-4}\]

Переписуючи це з точки зору негативних логарифмів, це стає

\[-\log [H_3O^+] = -\log K_a - log [HA] + \log[A^-] \label{2-5}\]

або, так як\(pK_a = –\log K_a\), ми інвертуємо співвідношення для збереження позитивного знака:

\[pH = pK_a + \log \dfrac{[A^-]}{[HA]} \label{2-6}\]

Це рівняння відоме як наближення Гендерсона-Хассельбальха. Це говорить нам, що рН розчину, що містить слабку кислотно-лужну систему, контролює відносні концентрації кислотної та базової форм цієї системи.

Цікаво відзначити, що рівняння H-H не було розроблено хіміками!

• Лоуренс Хендерсон (1878-1942) був американським лікарем, який викладав у Гарварді і вивчав кислотність крові та її відношення до дихання. У 1908 році він розробив відношення, показане в Рівнянні\(\ref{2-3}\).
• У 1916 р. Хассельбальх, фізіолог з Копенгагена, вивів логарифмічну форму в Рівнянні\(\ref{2-6}\).

Ви можете здивуватися, чому ці два рівняння, виведення яких ми зараз вважаємо майже тривіальним, мали увічнити імена цих двох вчених. Відповідь полягає в тому, що теорія хімічної рівноваги все ще розвивалася на початку 1900-х років, і ще не пробилася в підручники хімії. Навіть поняття рН було невідомим до тих пір, поки робота Соренсона не з'явилася в 1909 році. Саме таємниця (і медична необхідність) розуміння того, чому задишка зробила кров більш лужною, а занадто швидке дихання зробило її більш кислою, що змусило роботу H&H в сучасну хімію.

Особливий інтерес представляє випадок, коли рН розчину кислотно-лужної системи встановлюється на величину його рК _а. Згідно з вищевказаним рівнянням, коли рН = pK _a, термін журналу стає нулем, так що співвідношення [AB ^—]/[HA] = 10 ⁰ = 1, що означає, що [HA] = [AB ^-]. Іншими словами, при установці рН розчину на значення pK _а кислотно-лужної пари концентрації кислотно- і лужних форм будуть ідентичними. Ця умова може бути зображено схематично на безпротонної енергетичній діаграмі:

Це говорить, по суті, що коли рН розчину, що містить як кислоту, так і її кон'юговану основу, робиться ідентичним кислоті pK _a, форми HA і A ^- мають однакові вільні енергії, і тому будуть присутні в рівних концентраціях.

Примітка

При установці рН розчину на значення pK _а кислотно-лужної пари концентрації кислотно- і лужних форм будуть ідентичними.

Виготовлення та використання буферних розчинів

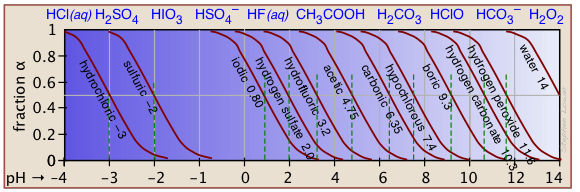
Буфери, як правило, найбільш ефективні, коли буферна система pK _a не надто далеко від цільового рН. У цих умовах як [ГА], так і [А ^—] досить великі, щоб компенсувати виведення або додавання, відповідно, іонів водню.

Таблиця\(\PageIndex{1}\): Загальні буферні системи

кислота	формули	пК а	діапазон рН
фосфорної	Н 2 РО 4/ГПО 4 ^—	2.16	1-3
вуглекислий	Н 2 СО 3 */ГСО 3 ^—	3.75	3-5
оцтової	ХОХО/ХОКО ^—	4.75	4-6
дигідрофосфат	Н 2 РО 4 ^— /ПО 4 ^2—	7.21	6-8
борний	Н 3 БО 3/Ч 2 БО 3 ^—	9.24	8-10
амонію	НЧ 4 ^+/ Н 3	9.25	8-10
бікарбонат	ГСО 3 ^—/СО 3 ^2—	10.3	9-11
моногідрофосфат	ХПО 4 ^2-/ПО 4 ^3—	12.3	11-13

Рівняння\(\ref{2-4}\) вище та його логарифмічний еквівалент у\(\ref{2-6}\) рівнянні мають обмежене використання в розрахунках, оскільки точні значення [A ^—] та [HA] відомі лише для особливого випадку, коли рН розчину ідентичний pK _a. Більшість буферних розчинів будуть пристосовані до інших рН, і, звичайно, як тільки буферний розчин почне робити це працювати, протидіючи ефекту додавання H ⁺ або OH ^-, і [A ^-] і [HA] зміниться. Ці два рівняння настільки широко використовуються в практичній хімії (і особливо в біохімії), що їх варто віддати пам'яті.

збільшує [Н ⁺] і знижує рН. Таким чином, ви завжди можете організувати рівняння, щоб воно вийшло правильно. З цих причин корисно переписати два вищевказані рівняння, замінивши рівноважні концентрації [A ^—] і [HA] відомими початковими значеннями C _a і C _b:

\[[H^+] \approx K_a \dfrac{C_a}{C_b} \label{2-7}\]

\[pH \approx pK_a + \log \dfrac{C_b}{C_a} \label{2-8}\]

Хоча це наближення, вони, як правило, виправдані, оскільки корисні буферні системи завжди значно концентровані, ніж ті, що відповідають за додавання або видалення іонів водню. Крім того, при цих більш високих іонних концентраціях K _a буферної системи рідко буде точно відомий. Не очікуйте, що фактичний рН буфера відповідатиме розрахункам краще, ніж 5%.

Приклад\(\PageIndex{2}\): Buffer Activity

Порівняйте ефекти додавання 1,0 мл 2,5 М HCl до

1. 100 мл чистої води
2. 100 мл 0,20 М розчину дигідрофосфату натрію.

Рішення

а)

1. кількість доданого HCl: (1,0 мл) × (2,5\ мм/мл) = 2,5 ммоль = 0,0025 моль
2. концентрація Н ⁺ в розчині: (0,0025 моль) ÷ (.101 л) = 0,025 М
3. рН = — журнал (.025) = 1,60, зміна рН = 1,60 — 7,00 = —5,4

б) (З таблиці\(\PageIndex{1}\), рК _а з Н ₂ РО ₄ ^— 7.21)

1. _{Початковий С а} (Н ₂ РО ₄ ^—) = С _б (ГПО ₄ ^2—) = 0,20 М
2. _{Початковий рН буферного розчину: рН = рН а+ лог (С б/С а) = 7,21+ 0 = 7,21}
3. Додано HCl перетворить 0,025 моль HPO ₄ ^2— до H ₂ PO ₄ ^-,
   змінюючи C _a на (.20 + .0025) моль ÷ (.101 л) = 2,00 М, і
   зменшуючи C _b до (.20 - 0,025) моль ÷ (0,101 л) = 1,95 М
4. Отриманий рН = 7,21 + лог (1,95/2,00) = 7,21 —.011 = 7,00
5. Зміна рН = 7,00 - 7,21 = —,21

Зверніть увагу, що в обох випадках рН знижується (як і повинно бути, якщо ми додаємо кислоту!) , але зміна набагато менше в буферному розчині.

Приклад\(\PageIndex{3}\): Buffer Preparation

Як би ви підготували 200 мл буферного розчину, рН якого становить 9,0?

Рішення

Першим кроком буде вибір сполученої кислотно-лужної пари, pK _a якої близький до потрібного рН. Дивлячись на наведену вище таблицю значень pK _a, підійде або борна кислота, або іон амонію. Для цього прикладу ми виберемо систему NH ₄ ⁺ /NH ₃, K _a = 5.5E—10, pK _a = 9.25.

2) Ми будемо використовувати Рівняння\(\ref{2-7}\) для визначення співвідношення C _a/ C _b, необхідного для установки [H ⁺] до потрібного значення 1,00 × 10 ^—9. Для цього випишіть повну рівноважну константу експресії для кислоти NH ₄ ⁺: NH ₄ ⁺ → NH ₃₊ H ⁺, а потім розв'яжіть його, щоб знайти необхідне співвідношення концентрації:

\ [K_a =\ dfrac {[NH_3] [H^+]} {[NH_4^+]} = 5.5\ раз 10^ {-10} \ nonumber\]

\ [\ dfrac {C_a} {C_b} =\ dfrac {[NH_3]} {[NH_4^+]} =\ dfrac {5.5\ раз 10^ {-10}} {[H^+]} =\ dfrac {5,5\ раз 10^ {-10}} {1,00\ раз 10^ {-9}} =\ dfrac {5.5\ раз 10^ {-10}} {10,00\ раз 10^ {-10}} = 0,55 \ nonumber\]

3) Найпростіший (якщо не особливо елегантний) спосіб вирішити це - спочатку припустити, що ми розчинимо 1,00 моль твердого NH ₄ Cl у воді, додамо достатню кількість OH ^- щоб частково нейтралізувати частину цієї кислоти відповідно до рівняння реакції NH ₄ ⁺ + ОН ^— → NH ₃₊ H ₂ O, а потім додати достатню кількість води, щоб вийшов об'єм 1,00 л.

маса хлористого амонію:

(1 моль) × (53,5 г М ол) = 53,8 г

нехай x = родимки NH ₄ ⁺, які повинні бути перетворені в NH ₃.
Тоді C _{a/C b} = (1- х)/х = .55; рішення цього дає х = .64, 1—х = .36.

4) Отже, щоб зробити 1 л буфера, розчиніть 0,36 × 53,8 г = 19,3 г твердого NH ₄ Cl в невеликій кількості води. Додайте 0,64 моль NaOH (найлегше зробити з вихідного розчину), а потім достатню кількість води, щоб вийшло 1,00 л.

5) Щоб зробити 200 мл буфера, досить помножити кожну з перерахованих вище цифр на 0,200.

Підводні камені наближення Гендерсона-Хассельбальха

Наближення Гендерсона-Хассельбальха широко використовується в практичних розрахунках. Те, що більшість книг не говорять вам, це те, що Eqution\(\ref{2-4}\) - це не більше, ніж «наближення наближення», яке може дати неправильні та оманливі результати при застосуванні до ситуацій, в яких спрощуючі припущення не є дійсними. Точна обробка спряжених кислотно-лужних пар, включаючи правильне виведення рівняння Гендерсона-Хассельбальха, наведено в розділі «Точні розрахунки».

Наближення Гендерсона-Хассельбальха справедливе лише для досить високих концентрацій

Наближення, що призводять до рівняння H-H, обмежують його надійне використання значеннями C _a і C _b, які знаходяться в межах порядку один від одного, і є досить високими. Також рК _а кислоти повинен бути помірним.

Малюнок 11.4.X:

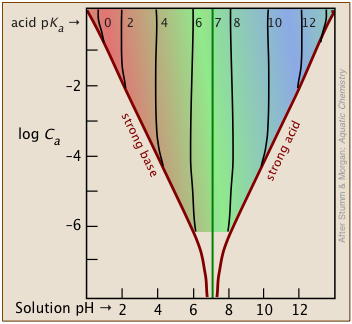
Затінена частина цього набору графіків вказує на значення C _a та K _a, які дають корисні результати. _{Зрозуміло, що чим менше буферна концентрація, тим вужче діапазон корисної кислоти pK a s. більшість буферних розчинів, як правило, досить концентровані, причому С а і С б зазвичай близько 0,01 - 0,1 М.} Таким чином, буфер на основі 0,01 М розчину кислоти, такої як хлорна (HClO ₃) з pK _a 1,9 буде падати безпосередньо за «безпечну» межу поблизу верхньої лівої частини діаграми.

\[\underbrace{[H^+] = K_a \dfrac{[HA]}{[A^-]}}_{\text{exact}} \label{2-9a}\]

Рівняння\(\ref{2-9a}\) - це просто перезапис виразу постійної рівноваги, і тому завжди вірно. Звичайно, не знаючи фактичних значень рівноваги [HA] і [A ^—], це співвідношення мало прямого використання в розрахунках рН.

\[\underbrace{[H^+] \approx K_a \dfrac{C_a}{C_b}}_{\text{approximate}} \label{2-9b}\]

\(\ref{2-9b}\)Рівняння ніколи не відповідає дійсності, але дасть хороші результати, якщо кислота досить слабка по відношенню до її концентрації, щоб зберегти [H ⁺] від занадто високої. _{В іншому випадку високий [Н ⁺] перетворить значну частку A ^— в кислотну форму HA, так що співвідношення [HA]/[A ^—] буде відрізнятися від C a/C b у двох вищезазначених рівняннях.} Споживання H ⁺ базою також підвищить рН вище прогнозованого значення, як ми бачили в попередньому прикладі проблеми.

Індекс буфера

Терміни інтенсивність буфера та буферна ємність зазвичай використовуються як синоніми буферного індексу, але в деяких контекстах буферна ємність позначає кількість сильної кислоти або сильної основи, яка змінює рН буфера на 1 одиницю. (див. Нижче). Наскільки ефективна дана буферна система в протистоянні змінам рН? Найбільш прямим вираженням цього є швидкість зміни рН, оскільки в систему додаються невеликі кількості сильної кислоти або основи: Δ C/Δ (рН). Виражається в численні числення, це буферний індекс, що визначається як

\[\beta = \left| \dfrac{dC}{d(pH)} \right| \label{2-19}\]

C тут мається на увазі концентрація сильної кислоти або основи, доданої в розчин. Оскільки додана кислота або основа впливають на рН протилежними способами, ми приймаємо абсолютне значення цієї функції для того, щоб переконатися, що β завжди позитивний. Значення β можна обчислити аналітично з C _a, C _b, K _a, K _b і [H ⁺]. Беручи другу похідну β, можна показати, що буферний індекс має максимальне значення, коли рН = pK _a.

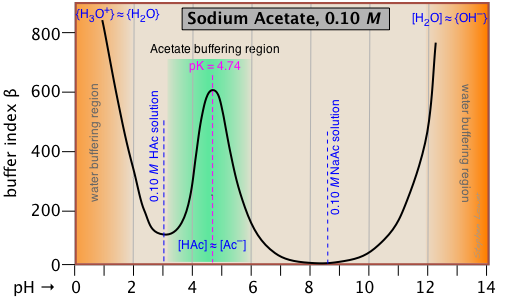
Цей графік буферного індексу для 0,10 М розчину ацетату натрію є типовим і підтверджує, що буферизація є найбільш ефективною в межах приблизно ± 1 рН одиниці pK _a. Але як щодо ще більшої буферизації, яка, мабуть, відбувається при двох крайностях рН (помаранчеве затінення)? Це пов'язано з буферизації, пов'язаної з самою водою, і буде видно у всіх водних буферних розчинами.

Чиста вода буферується кон'югатною парою H ₃ O ^+/H ₂ O при дуже низькому рН, а H ₂ O/OH- при високому рН. Це легко зрозуміти, якщо ви думаєте про додавання деякої сильної кислотної кислоти в чисту воду; навіть одна крапля HCl призведе до зниження рН до 0. Якщо ви продовжуєте додавати кислоту, рН не опуститься значно нижче 0, оскільки не буде достатньо вільних молекул води, що залишаються для гідратації HCl для отримання іонів H ₃ O ⁺ - таким чином розчин сильно буферизований.

Зауважте, що якби ми віднімали ефект буферизації NaAC з наведеного вище графіка, залишилася ділянка для самої води виявила б мінімум при рН 7, де обидва [H ₃ O ⁺] і [OH ^-] поділяють загальне мінімальне значення.

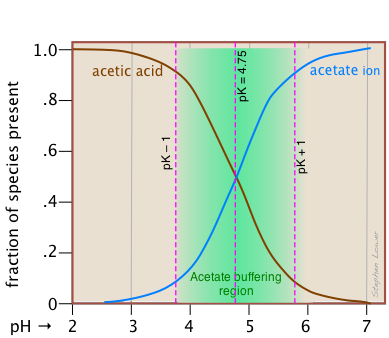
Цей альтернативний погляд показує, як фракції розподілу HaC та Ac ^{— пов'язані з} ефективним діапазоном буферизації цієї сполученої пари, який умовно визначається як ± 1 одиниця рН pK _a. Термін буферна ємність є альтернативним засобом вираження здатності буферної системи поглинати додавання сильної кислоти або основи, не викликаючи відхилення рН більш ніж на одну одиницю від чистого буфера.

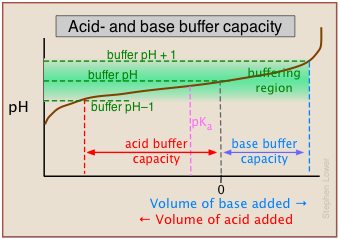
У цьому прикладі буферні ємності для додавання кислоти та основи будуть відрізнятися, оскільки буферний рН був відрегульований до значення, яке відрізняється від його pK _a.

Важливість концентрації буфера

Буферні системи повинні бути значно більш концентрованими, ніж концентрації сильної кислоти або основи, які вони повинні поглинати, залишаючись в межах бажаного діапазону pH. Після того, як додана кислота або основа споживають більшу частину того чи іншого кон'югатного виду, що містить буфер, рН більше не стабілізується. І звичайно, дуже малі буферні концентрації будуть наближатися до рН чистої води.

Більш повний вигляд: Log-C проти pH графіки

Ці ділянки часто називають ділянками Сіллена. Ларс Гуннар Сіллен (1916-1970) був шведським хіміком, який вивчав розподіл іонних видів у водних розчині і особливо в океанах. Оскільки концентрації сполучених видів можуть варіюватися на багато порядків, набагато корисніше виражати їх за логарифмічною шкалою. Оскільки рН вже логарифмічний, то можна отримати «вид з висоти пташиного польоту» кислотно-лужної системи на компактному колодному ділянці.

Навіть краще, ці сюжети легко будуються без будь-яких розрахунків або арифметики - або навіть будь-якого графічного паперу - будь-якого скрапкового паперу, навіть зворотного боку конверта, буде достатньо. Лінійка або інший прямий край дадуть, однак, більш точні результати. Крім того, ви можете використовувати ці графіки для оцінки рН розчину монопротової або поліпротової кислоти або основи без боротьби з квадратними або рівняннями вищого порядку - або робити будь-яку арифметику взагалі! Результати не будуть такими точними, як ви могли б отримати від правильного числового рішення, але з огляду на невизначеність того, як константи рівноваги впливають на наявність інших іонів у розчині, це рідко є проблемою.

Окрім цих переваг, використання графіків Log-C проти рН дозволить вам зрозуміти хімію кислотно-лужних систем, які неможливо отримати, просто зробивши числові розрахунки. Основна форма сюжету, і відправна точка для будь-якого використання таких ділянок, виглядає так:

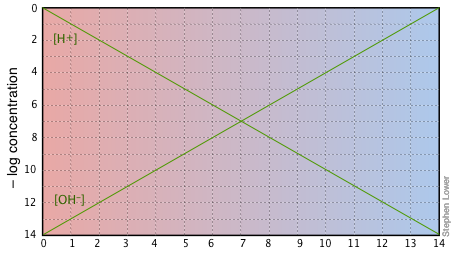
Якщо ви уважно вивчите цю ділянку, то побачите, що це не що інше, як визначення рН і pH, а також визначення нейтрального розчину при рН 7. Зверніть увагу, наприклад, що коли рН дорівнює 4,0, [Н ⁺] = 10 ^—4 М і [ОН ^—] = 10 ^—10 М.

Простий приклад: розчин оцтової кислоти

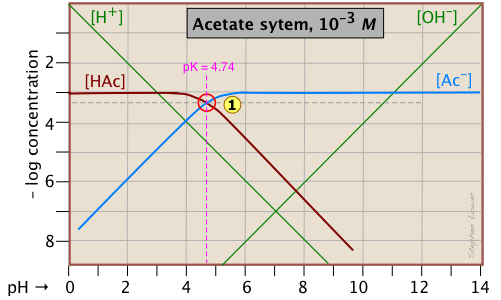
Ось ділянка колоди С на 10 ^-3 М розчин оцтової кислоти («HaC») у воді. Хоча спочатку це може виглядати трохи складним, це дійсно дуже просто. Важка бордова лінія зліва позначає концентрацію кислоти HaC як функцію рН. Синій рядок праворуч показує, як концентрація бази Ac ^— залежить від рН. Горизонтальні частини цих ліній вирівнюються з «3» на осі —log- C, що відповідає номінальній концентрації 10 ^—3 М (С _а).

Як ми знаємо форми та розміщення ділянок для концентрацій оцтової кислоти [HaC] та ацетатного іона [Ac ^—]? Хоча обидві ці концентрації, звичайно, будуть змінюватися в залежності від рН, їх відхилення від 10 ^—3 М занадто малі, щоб виявити себе на логарифмічному графіку, поки рН не наблизиться до pK _a.

• При дуже низькому рН практично вся ацетатна система буде знаходитися в кислому вигляді (тобто [HaC] = 10 ^—3), і аналогічно при високому pH базова форма [Ac ^—] = 10 ^—3 М.
• Коли рН = pK _a, концентрації сполучених видів ідентичні, про що вказує перетин ліній, що представляють дві концентрації. Ці концентрації становитимуть половину загальної концентрації, заданої C _a, тому [HaC] = [Ac ^-] = ½ C _a = 0.5E—3 M. Куди це дівається на осі Log-C? Ну, логарифм 0,5 дорівнює —0,3 (корисний факт, щоб пам'ятати!) , Таким чином, точка перетину в зміщується на 0,3 одиниці Log-C нижче рівня —3 на осі y.
• Оскільки точка визначає як pK _а, так і концентрацію певної кислотно-лужної системи, вона відома як системна точка.
• А як щодо схилів ділянок, коли вони нахиляються вниз? Виходить, що ці схили складають +1 для
  [Ac ^—] і —1 для [haC]. Оскільки нахили ліній для [H ⁺] та [OH ^—] дорівнюють ± 1, ми можемо використовувати їх як орієнтири; просто зробіть ділянки [Ac ^—] та [HA] паралельно їм.
• Вигнуті частини сюжету, який з'єднує горизонтальну та діагональну частини по обидва боки системної точки, можна намалювати від руки без зайвої помилки; логарифмічні ділянки дуже прощають!

Оцінка рН

Особливий інтерес в кислотно-лужній хімії представляють значення рН розчину кислоти і її кон'югатної основи в чистій воді; як відомо, вони відповідають точкам початку і еквівалентності при титруванні кислоти з сильною основою. Продовжуючи приклад системи оцтової кислоти, ми показуємо нижче ще один сюжет, подібний до наведеного вище, але з доданими ще кількома рядками та цифрами.

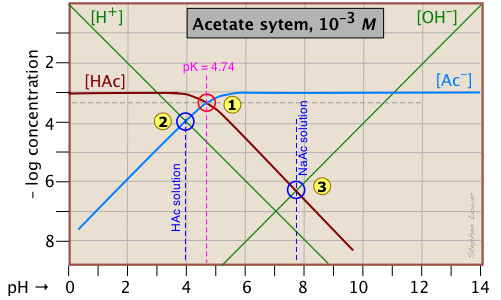
рН оцтової кислоти в чистій воді. Припустимо, ви хотіли б знайти рН 0,001 М розчину оцтової кислоти в чистій воді. З рівняння

\[HAc + H_2O \rightleftharpoons H_3O^+ + Ac^– \label{Acetate 2-1} \]

we know that equal numbers of moles of hydronium and acetate ions will be formed, so the concentrations of these species should be about the same:

\[[H^+] \approx [Ac^–] \label{Acetate 2-2}\]

will hold. The equivalence of these two concentrations corresponds to the point labeled on the logC-pH plot; this occurs at a pH of about 4, and this is the pH of a 0.001 M solution of acetic acid in pure water.

pH of sodium acetate in pure water. A 0.001 M solution of NaAc in water corresponds to the composition of a solution of acetic acid that has been titrated to its equivalence point with sodium hydroxide. The acetate ion, being the conjugate base of a weak acid, will undergo hydrolysis according to

\[Ac^– + H_2O \rightleftharpoons HAc + OH^– \label{Acetate 2-3}\]

which establishes the approximate relation

\[[HAc] \approx [OH^–] \label{Acetate 2-4}\]

This condition occurs where the right sloping part of the line representing [HAc] intersects the [OH^–] line at in the plot above. As you would expect for a solution of the conjugate base of a weak acid, this corresponds to an alkaline solution, in this case, at about pH = 7.8.

You will have to admit that estimating a pH in this way is far more painless than an ordinary numerical calculation would be!

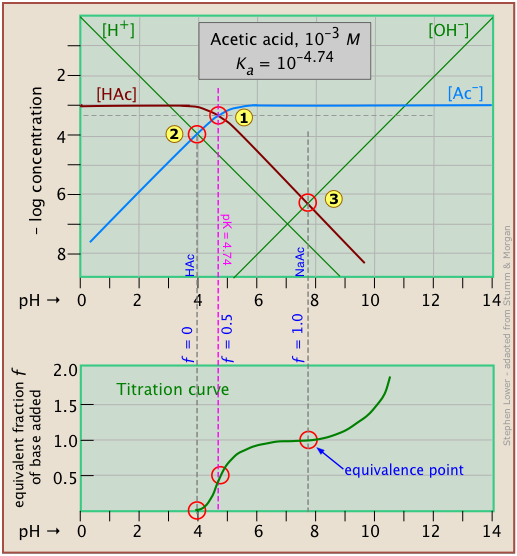
It is interesting to show the Sillén plot for a weak acid system with its titration curve, both on the same pH scale. In this example, the titration plot has been turned on its side and reversed in order to illustrate the correspondence of its ƒ=0 (initial), ƒ=0.5 and ƒ=1 (equivalence) points with the corresponding points on the upper plot.

Ammonia - a weak base

Ammonia, unlike most gases, is extremely soluble in water. Solutions of NH₃ in water are properly known as aqueous ammonia, NH₃(aq); the name "ammonium hydroxide" is still often used, even though there is no evidence to suggest that a species NH₄OH exists. Ammonia is the conjugate base of the ammonium ion NH₄⁺. The fact that ammonia is a base has no special significance insofar as the construction and interpretation of the log-C vs pH diagram is concerned; such diagrams always refer to conjugate acid-base systems, rather than to individual acids and bases.

Thus the system point defines the NH₄⁺/NH₃ pair (pK_a 9.3) at 25°C and a total concentration

\[C_T = C_a + C_b = 0.0010\; M. \label{NH3 2-5}\]

To estimate the pH of a solution of ammonia in pure water, we make use of the charge balance requirement (known as the proton condition)

\[[NH_4^+] + [H^+] = [OH^-] \label{NH3 2-5.5}\]

which we simplify by assuming that, because NH₄⁺ is a weak acid, [NH₄⁺] >> [H⁺] and we can drop the [H⁺] term; thus the approximation

\[[NH_4^+] \approx [OH^-] \label{NH3 2-6}\]

which corresponds to the crossing point and a pH of 10.0. Similarly, at the crossing point , [NH₃] ≈ [H⁺]. This comes from the proton condition

\[[NH_3] + [H^+] – [OH^–] = 0 \label{NH3 2-7}\]

by dropping the [OH^–] term on the assumption that its value is negligible compared to [H⁺].

Equation \(\ref{NH3 2-7}\) is referred to as the "proton condition". Sorry to sneak it in without warning, but we hope that having piqued your curiosity, you might take the time to look at the following discussion of this important tool for estimating the pH of a solution of a pure acid, base, or a salt.

Mass- and charge balance, and the proton condition

In any aqueous solution of an acid or base, certain conservation conditions are strictly observed. Together with concentration and the K_a or K_b , these put certain constraints on the system that determine the state of the system. The most fundamental of these are conservation of mass and of electric charge, which of course apply to chemical changes of all kinds. We commonly express these as mass balance and charge balance, respectively. (The latter of these is sometimes referred to as the electroneutrality condition.)

Using the above example of the ammonium system as an illustration of this, we are interested in two particular instances of practical importance: what conditions apply to solutions made by dissolving a) pure ammonia, or b) ammonium chloride, in water?

Sillén diagram

Charge balances

C_{T, NH3} = [NH₃] + [NH₄⁺] = 10^–2 M

C_{T, Ac} = [HAc] + [Ac^–] = 10^–2 M

NH₃: [H⁺] + [NH₄⁺] = [OH^–]

NaAc: [Na⁺] + [H⁺] = [Ac^–] + [OH^–]

OK so far? That's really all we need, but it's usually more convenient to combine these with mass balances on the protons alone, so that we have a single equation for each of the two solutions. The resulting equations are known as the proton conditions for the two solutions.

To avoid a lot of algebra, there is a simple short-cut for writing a proton condition equation:

1. Identify the substance you are starting with — the pure acid, base, or salt, and also H₂O itself, that make up the solution whose pH you wish to know at the concentration for which the log C-pH chart is drawn. we call this the proton reference level (if that appellation scares you, it is sometimes referred to as the "basis substance".)
2. On the left side of the proton condition, write concentration expressions for all species that possess protons in excess of the reference level.
3. On the right side, write concentrations of all species that possess fewer protons the reference level.

Let's try it for our ammonia system.

Solution of NH₃ in water:

The proton reference level (PRL) is defined by NH₃(aq) and H₂O.

Proton condition: [H₃O⁺] + [NH₄⁺] = [OH^–]

(Notice that the substances that define the PRL (in case, H₂O and NH₃) never appear in the proton condition equation.)

Solution of NH₄Cl (or of any other strong-anion ammonium salt) in water:

The PRL is defined by NH₄⁺ and H₂O.

Proton condition: [H₃O⁺] = [NH₃] + [OH^–]

(The chloride ion has nothing to do with protons, so it does not appear here.)

This proton condition stuff seems awfully complicated: why do we bother?

Good question: the answer is that what seems complicated at first sometimes turns out to be simpler and easier to understand than any alternative. Think of it this way: acid-base reactions involve the transfer of protons: some protons jump up to higher proton-free energy levels (e.g., NH₃ + H₂O → NH₄⁺ + OH^–), others drop down to proton-vacant levels (H₃O⁺ → NH₃ → H₂O + NH₄⁺). But no matter what happens, the total number of "available" protons (that is, all "dissociable" protons, including those in H₃O⁺) must be conserved — thus the "mass balance on protons". So let's look again at the log C - pH plot for the ammonium system, which we reproduce here for your convenience:

Consider first the solution of ammonium chloride, whose proton condition is given by [H₃O⁺] = [NH₃] + [OH^–]. We know that NH₄Cl, being the salt of a weak base and a strong acid, will give a solution that is slightly acidic. In such a solution, [OH^–] will be quite small so that we can neglect it without too much error. We can then write the proton condition as [H⁺] ≈ [NH₃]. On the plot above, this corresponds to point where the lines representing these quantities cross. At this pH of around 6.2, [OH^–] is about two orders of magnitude smaller than [NH₃], so we are justified in dropping it.

Similarly, for a solution of ammonia in water, the proton condition [H₃O⁺] + [NH₄⁺] = [OH^–] that we worked out above can be simplified to [NH₄⁺] ≈ [OH^–] (point ) with hardly any error at all, since [H⁺] is here about six orders of magnitude smaller than [NH₄⁺].

In our discussion of the plot for the acetic acid system, we arrived at the proton conditions [H⁺] ≈ [Ac^–] (for HAc in water) and [H⁺] ≈ [OH^–] (for NaAc) by simply using the stoichiometries of the reactions. This can work in the simplest systems, but not in the more complicated ones involving polyprotic systems. In general, it is far safer to write out the complete proton condition in order to judge what concentrations, if any, can be dropped.

Ammonium acetate solution: solution of a salt

Having looked at the Sillén diagrams for acetic acid and ammonia, let's examine the log C-pH plot for this salt of acetic acid and ammonia.

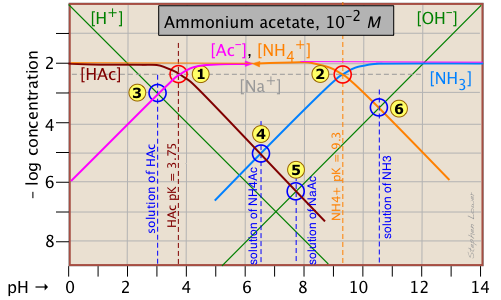
You will recall that we dealt with solutions of the salts sodium acetate and ammonium chloride in the two examples described above. What is different here is that both components of the salt CH₃COONH₄ ("NH₄Ac") are "weak" in the sense that their conjugate species NH₃ and HAc are also present in significant quantities. This means that we are really dealing with two acid-base systems — the ones shown previously — on the same plot.

Each system retains its own system point, for the acetate system and для амонійної системи. Зауважте, що два показані раніше графіки були для ^10-3 М розчинів, тому несистемні точки для цього більш концентрованого розчину виникають при різних значеннях рН. РН ^10-2 М розчинів HaC, NaAC та NH ₃ розташовані за допомогою тих самих протонних умов, що і раніше.

Єдине нове тут - точка, яка відповідає розчину ацетату амонію, в якому нас цікавить. Протонною умовою для цього розчину є [H ⁺] + [HaC] = [NH ₃ (aq)] + [ОН ^—]. Огляд ділянки показує, що [H ⁺] << [haC] і [OH ^—] << [NH ₃ (aq)], тому умова протона може бути спрощена до [haC] ≈ [NH ₃ (aq)], що відповідає перетину цих двох ліній при .

Поліпротичні системи

Тепер, коли ви можете знайти свій шлях навколо log c-pH ділянки, які охоплюють дві кислотно-лужні системи, поліпротичні системи, які ми описуємо нижче, не повинні бути проблемою взагалі.

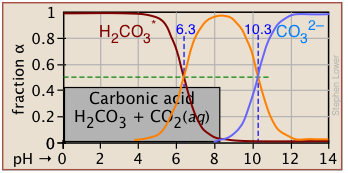
Карбонатна система

Ретельне розуміння вуглекислотно-карбонатної системи має важливе значення для розуміння хімії природних вод та біохімії дихання у людини та інших тварин. Є дві особливі речі про цю систему, які вам потрібно знати:

• Розчин вуглекислого газу у воді переважно у вигляді гідратованих СО ₂, СО ₂ (aq). Але невелика частка розчиненого СО ₂ вступає в реакцію з водою з утворенням вугільної кислоти, Н ₂ СО ₃. Оскільки цю кислоту неможливо виділити, звичайною практикою є додавання зірочки до формули для позначення «загальної» концентрації CO ₂
  [CO ₂ + H ₂ CO ₃]: таким чином H ₂ CO ₃ *.
• Оскільки СО ₂ є газом, розчини, що містять карбонатні види всіх видів, можуть врівноважуватися з атмосферою, яка зазвичай містить невеликі кількості СО ₂. Це означає, що відкритий для атмосфери розчин бікарбонату натрію може втрачати СО ₂ в атмосферу при низькому рН, і поглинати його при високому рН. Система такого роду, як кажуть, відкрита. Крім того, система може бути закрита для обміну з атмосферою. Ділянки Sillén для відкритих і закритих карбонатних систем мають дуже різний вигляд.

Цей сюжет Сіллена для закритої системи H ₂ CO ₃ * характерний для інших систем дипротової кислоти тим, що існує три сполучені види та дві системні точки. Концентрація 10 ^—3 М, побудована тут, характерна для того, що міститься в грунтових водах, які контактують з карбонатними відкладеннями.

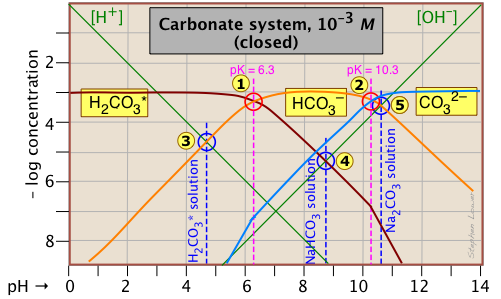
Показники рН 10 ^—3 М розчину CO ₂, NaHCO ₃ і Na ₂ CO ₃ вказуються синіми анотаціями.

розчинений, (еталонний рівень)	стан протона	наближення
вуглекислий газ (H 2 CO 3 *)	[Н ^+] = [НСО 3 ^—] + 2 [СО 3 ^2—] + [ОН ^-]	[H ^+] ≈ [ГСО 3 ^—]
бікарбонат натрію (NaHCO 3)	[Н ^+] + [Н 2 СО 3] = [СО 3 ^2—] + [ОН ^-]	[Н 2 СО 3] ≈ [ОН ^-]
карбонат натрію (Na 2 CO 3)	[Н ^+] + 2 [Н 2 СО 3 *] + [ГСО 3 ^-] = [ОН ^-]	[ГСО 3 ^-] ≈ [ОН ^-]

Вам слід взяти кілька хвилин, щоб перевірити наближення в крайньому правому стовпці. Зверніть увагу на фактори 2, які множать деякі концентрації. Наприклад, термін «2 [CO ₃ ^2—]» у першому рядку таблиці означає, що вид CO ₃ ^2— знаходиться в двох кроках від еталонного рівня протона H ₂ CO _3*, тому для збалансування одного карбонатного іона знадобиться два іони водню.

Ще однією новою особливістю, введеною тут, є подвоєння нахилів ліній, що представляють [H ₂ CO ₃ *] і [CO ₃ ^2—], де вони перетинають значення рН, що відповідають K _a s, які є одним кроком, видаленим із власних точок системи. і близько —журнал C = 7.

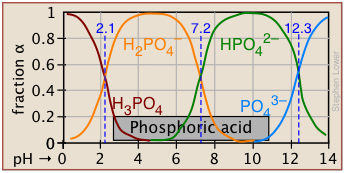
Фосфатна система

Ця трипротна система широко використовується для приготування буферних розчинів в біохімічних додатках. У своїй фундаментальній формі тут немає нічого нового, крім додаткової системної точки, відповідної pK _a H ₂ PO ₄ ^—.

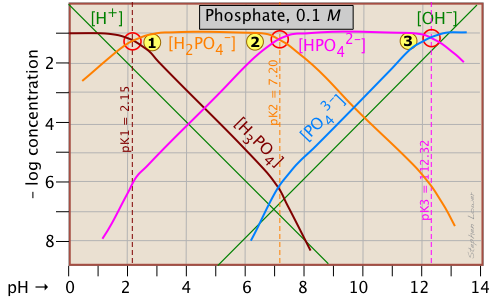
РН ^{10-3 М розчинів H ₃} PO ₄, NaH ₂ PO ₄, Na ₂ HPO ₄ і Na ₃ PO ₄ можна оцінити, встановивши протонні умови наступним чином. На жаль, ці оцінки дещо ускладнюються через близькість трьох системних точок. Але це набагато простіше, ніж робити числове рішення, яке вимагає вирішення полінома п'ятого ступеня!

розчинений, (еталонний рівень)	стан протона	наближення
фосфорна кислота (H 3 PO 4)	[Н ^+] = [Н 2 РО 4 ^—] + 2 [ГПО 4 ^2—] + 3 [РО 4 ^3—] + [ОН ^—]	[Н ^+] ≈ [Н 2 РО 4 ^—]
дигідрофосфат натрію (NAh 2 PO 4)	[Н ^+] + [Н 3 РО 4] = [ГПО 4 ^2—] + 2 [РО 4 ^3—] + [ОН ^—]	[Н ^+] + [Н 3 ПО 4] ≈ [ГПО 4 ^2—]
динатрію гідрофосфат (Na 2 HPO 4)	[Н ^+] + 2 [Н 2 РО 4 ^—] + [Н 2 РО 4 ^—] = 3 [РО 4 ^3—] + [ОН ^—]	[Н 3 РО 4 -] = [РО 4 ^3—] + [ОН ^-]
тринатрійфосфат (Na 3 PO 4)	[Н ^+] + 3 [Н 3 РО 4] +2 [Н 2 РО 4 ^—] + [ГПО 4 ^2—] = [ОН ^—]	[HP 4 ^2—] ≈ [ОН ^-]

Оскільки ділянка фосфатів досить переповнена, ми показуємо тут модифікований, в якому підкреслюються деталі оцінок рН для розчинів H ₃ PO ₄ та його солей.

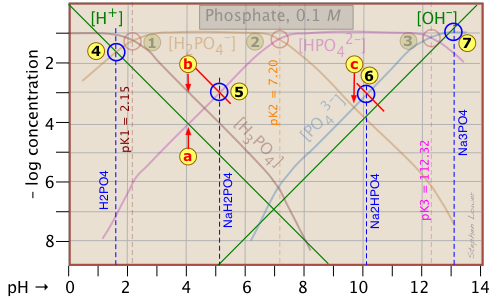
Оцінка рН ^10-3 М розчинів фосфорної кислоти і тринатрійфосфату, заснована на наближеннях у наведеній вище таблиці, є нескладною.

Однак ті, що _{стосуються} NaH _{2 PO 4 та Na 2 HPO 4}, ускладнюються наявністю двох концентраційних термінів на правій стороні відповідних наближень умов протонів.

Якщо ви не перебуваєте в просунутому курсі, ви можете пропустити наступні деталі. Важливо знати, що графічні оцінки цих більш проблемних систем принципово можливі.

Таким чином, для дигідрофосфату натрію, якби ми слідували шаблону інших систем, наближення в точці перетину було б
[H ⁺] = [HPO ₄ ^2—], що відповідає точці. Але огляд ділянки показує, що при цьому рН (4,0) концентрація Н ₃ РО ₄ в десять разів більше, ніж у Н ⁺ (точка). Приблизну оцінку рН можна зробити шляхом побудови лінії (показаної червоним кольором), яка паралельна тим для Н ₃ РО ₄ і Н ⁺, але піднята вгору на коефіцієнт 10. Це призводить до нового пункту перетину.

Аналогічно, рН розчину динатрію гідрофосфату не відповідає точці перетину через значне значення [HPO ₄ ^3—] при цьому рН. Знову ж таки, ми будуємо лінію над цією точкою перетину, яка передбачає рН, що відповідає точці.

Хоча ці стратагеми можуть здатися досить грубими, слід зазначити, що невизначеності, пов'язані з ними, як правило, мінімізуються на логарифмічному графіку. _{Крім того, слід враховувати, що в розчині, настільки концентрованому, як 0,1 М, значення рК, знайдені в таблицях, непридатні.} Альтернатива розв'язання для рН алгебраїчно з урахуванням коефіцієнтів активності для високих іонних концентрацій рідко варта зусиль.

Як намалювати діаграми Сіллена

Зв'язок між рН розчину і концентраціями слабких кислот і їх кон'югатних видів є алгебраїчно досить складним. _{Але на більшій частині діапазону рН можна зробити спрощення припущення, що при вираженні в логарифмічній формі графік як прямі лінії, що мають інтегральні ухили 0, ± 1, ± 2 і т.д. тільки в межах вузького діапазону рН поблизу pK а ці спрощення припущення руйнуються, але на} логарифмічний графік, можна намалювати плавну криву, яка охоплює цей діапазон, не вносячи значної помилки.

Ось ваші основні канцелярські товари - сюжет із зображенням двох іонів, які завжди присутні в будь-якому водному розчині. На практиці зазвичай можна відрізати нижню частину, де концентрації менше\(10^{–10}\, M\).
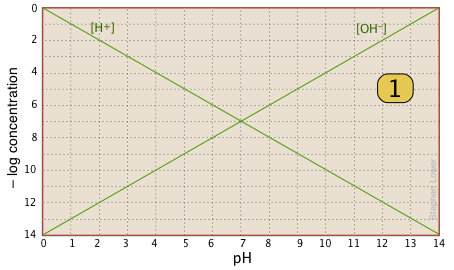Для будь-якої даної кислотно-лужної системи потрібно знати рК а і номінальну концентрацію КТ. Знайдіть точку, в якій ці дві лінії перетинаються.
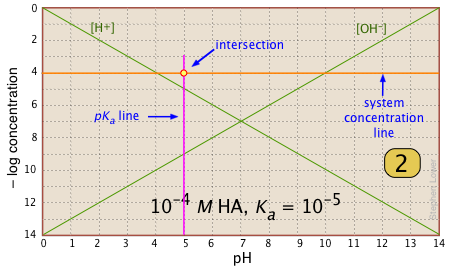Знайдіть і позначте системну точку на pK лінію. Це буде 0,3 одиниці Log-C нижче лінії концентрації. Це де [ГА] = [А ^—] = ½ С т. (Нагадаємо, що log.5 = .3)
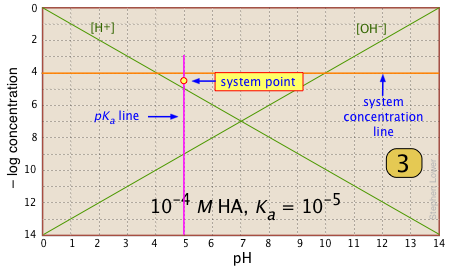Для pH < pK a, [HA] показує лінію через точку системи з нахилом = 0. Для pH > pK a лінія передбачає нахил —1. Використовуйте лінії [H ^+] та [OH ^—] як напрямні.
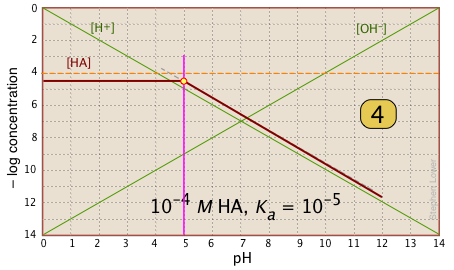У інтервалі pH ± pK a нахил змінюється від 0 до +1. Ви можете наблизити це за допомогою похилої лінії, як показано, або «прикрасити» її плавною кривою.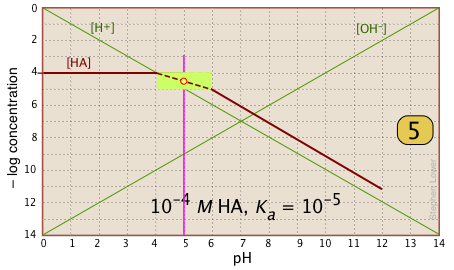
Нарешті, намалюйте лінії для сполученої форми [A ^—], використовуючи нахили +1 і 0.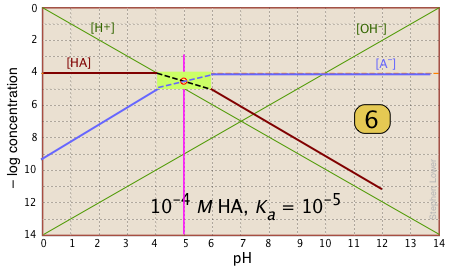

Для чого все це добре?

Припустимо, у вас є розчин NaA, рН якого дорівнює 8. Оцініть концентрацію кислоти ГК в розчині. Все, що вам потрібно зробити, це подивитися на сюжет. Лінія [HA] перетинає лінію, що позначає цей рН при — log C = 6, або [HA] = 10 ^—6. Ця величина занадто мала, щоб значно зменшити [А ^—], яка залишається при приблизно КТ = 10 ^—6 М.

Посилання

1. Безмежні обриси на буферних розв'язках. Вони узагальнюють основні моменти та приклади проблем, представлені в основних підручниках. Вони є відмінним помічником для попереднього огляду іспиту. Хімія: Центральна наука (8 підтем)
2. Колекція практичних вправ (з розчинами) на буферах та титруваннях від Bryn Mawr College.
3. Рівняння Гендерсона-Хассельбальха: його історія та обмеження - Генрі Н. По і Н.М.Сеноза, Дж. Ред. 78 (11) 2001 (1499-1503)
4. Детальну обробку діаграм Log-C vs pH можна знайти в книзі Кислотно-лужні діаграми Калерта та Шотца. Він доступний в Інтернеті в деяких бібліотеках коледжів.