4.6: Значні цифри та округлення
- Page ID
- 19247
- Наведіть приклад вимірювання, число значущих цифр якого явно занадто велике, і поясніть чому.
- Зазначте мету округлення та опишіть інформацію, яку потрібно знати, щоб зробити це належним чином.
- Округлення числа до вказаної кількості значущих цифр.
- Поясніть, як округлити число, друга за значимістю цифра якого дорівнює 9.
- Провести простий розрахунок, який передбачає дві і більше спостережуваних величин, і висловити результат у відповідній кількості значущих цифр.
Чисельні значення, з якими ми маємо справу в науці (і в багатьох інших аспектах життя), представляють вимірювання, значення яких ніколи не відомі точно. Наші кишенькові калькулятори або комп'ютери цього не знають; вони розглядають числа, які ми пробиваємо в них, як «чисті» математичні сутності, в результаті чого операції арифметики часто дають відповіді, які фізично смішні, хоча математично правильні. Мета цього блоку - допомогти вам зрозуміти, чому це відбувається, і показати вам, що з цим робити.
Цифри: Значущі та інші
Розглянемо два твердження, показані нижче:
- «Населення нашого міста - 157 872 населення».
- «Кількість зареєстрованих виборців станом на 1 січня становила 27 833.
Яке з них ви б виправдали, негайно звільнивши? Звичайно, не другий, тому що він, ймовірно, походить з бази даних, яка містить один запис для кожного виборця, тому число можна знайти просто підраховуючи кількість записів. Перше твердження не може бути правильним. Навіть якщо населення міста може бути визначено точно (Постійні жителі? Теплі тіла?) , як ми можемо враховувати хвилинні зміни, які відбуваються, коли люди народжуються і вмирають, або переїжджають і віддаляються?
Яка різниця між двома номерами населення, зазначеними вище? Перша виражає величину, яку неможливо точно знати — тобто вона несе в собі ступінь невизначеності. Цілком можливо, що останній перепис дав саме 157 872 записи, і що це може бути «населення міста» в легальних цілях, але це точно не «справжнє» населення. Щоб краще відобразити цей факт, можна перерахувати населення (наприклад, в атласі) як 157 900 або навіть 158 000. Ці дві величини були округлені до чотирьох і трьох значущих цифр відповідно і мають такі значення:
- 1579 00 (значущі цифри підкреслені тут) означає, що населення, як вважають, знаходиться в межах близько 1578 50 до приблизно 1579 50. Іншими словами, населення становить 1579 00±50. Додавання до цього числа «плюс або мінус 50» означає, що ми вважаємо абсолютну невизначеність вимірювання популяції 50 — (—50) = 100. Можна також сказати, що відносна невизначеність становить 100/157900, яку ми також можемо висловити як 1 частину в 1579 році, або 1/1579 = 0,000633, або близько 0,06 відсотка.
- Значення 158 000 означає, що населення, ймовірно, між 157 500 і 158 500, або 158 000 ± 500. Абсолютна невизначеність 1000 перетворюється на відносну невизначеність 1000/158000 або 1 частина в 158, або близько 0,6 відсотка.
Яке з цих двох значень ми повідомляємо як «населення», буде залежати від ступеня впевненості, яку ми маємо до початкової цифри перепису; якщо перепис був завершений минулого тижня, ми могли б округлити до чотирьох значущих цифр, але якщо це було рік або близько того тому, округлення до трьох місць може бути більш розумним вибором. У такому випадку немає дійсно об'єктивного способу вибору між двома альтернативами.
Це ілюструє важливий момент: поняття значущих цифр має менше спільного з математикою, ніж з нашою впевненістю у вимірюванні. Ця впевненість часто може бути виражена чисельно (наприклад, висота рідини в вимірювальній трубці може бути прочитана до ± 0,05 см), але коли це не може, як у нашому прикладі населення, ми повинні залежати від нашого особистого досвіду та судження.
Отже, що таке значуща цифра? Згідно зі звичайним визначенням, це всі числівники в виміряній кількості (рахуючи зліва) значення яких вважаються відомими точно, плюс ще один, значення якого могло б бути на один більше або на один менше:
- У «1579 00» (чотири значущі цифри) залишаються найбільш три цифри точно відомі, але четверта цифра «9» цілком може бути «8», якщо «істинне значення» знаходиться в межах передбачуваного діапазону від 1578 50 до 1579 50.
- У «158 000» (три значущі цифри) найбільш ліві дві цифри відомі точно, тоді як третя цифра може бути або «7», або «8», якщо істинне значення знаходиться в межах передбачуваного діапазону від 157 500 до 158 500.

Хоча округлення завжди призводить до втрати числової інформації, те, від чого ми позбавляємося, можна вважати «числовим шумом», який не сприяє якості вимірювання. Мета округлення полягає в тому, щоб уникнути вираження значення з більшою мірою точності, ніж узгоджується з невизначеністю вимірювання.
Якщо ви знаєте, що баланс точний з точністю до 0,1 мг, скажімо, то невизначеність при будь-якому вимірюванні маси, проведеному на цьому балансі, складе ± 0,1 мг. Припустимо, однак, що вам просто кажуть, що об'єкт має довжину 0,42 см, без вказівки на його точність. У цьому випадку все, що вам доведеться йти далі, - це кількість цифр, що містяться в даних. При цьому кількість «0,42 см» вказана до 0,01 одиниці в 0 42, або одна частина в 42. Мається на увазі відносна невизначеність в цьому показнику становить 1/42, або близько 2%. Тому точність будь-якої числової відповіді, обчисленої за цим значенням, обмежена приблизно однаковою сумою.
Помилка округлення
Важливо розуміти, що кількість значущих цифр у значенні забезпечує лише приблизне вказівку на його точність, і що інформація втрачається при округленні. Припустимо, наприклад, що ми вимірюємо вагу об'єкта як 3,28 г на балансі, який вважається точним до ± 0,05 грама. Отримане значення 3,28 ± 0,05 грам говорить нам, що справжня вага об'єкта може бути десь між 3,23 г і 3,33 г Абсолютна невизначеність тут становить 0,1 г (± 0,05 г), а відносна невизначеність становить 1 частина в 32,8, або близько 3 відсотків.
Скільки значущих цифр повинно бути в повідомленому вимірі? Оскільки лише лівий самий «3» у «3.28" є впевненим, ви, ймовірно, вирішили округлити значення до 3.3 м Поки що так добре. Але що хтось інший повинен зробити з цієї цифри, коли вони бачать її у вашому звіті? Значення «3,3 г» передбачає неявну невизначеність 3,3 ± 0,05 г, що означає, що істинне значення, ймовірно, між 3,25 г і 3,35 г Цей діапазон на 0,02 г нижче, ніж пов'язаний з початковим вимірюванням, і тому округлення ввело зміщення цієї кількості в результат. Оскільки це менше половини невизначеності ± 0,05 г при зважуванні, це не дуже серйозна справа сама по собі. Однак, якщо кілька значень, які були округлені таким чином, об'єднані в розрахунку, помилки округлення можуть стати значними.
Правила округлення
Стандартні правила округлення добре відомі. Перш ніж ми їх викладемо, давайте домовимося про те, що називати різні складові числового значення.
- Найбільш значуща цифра - це ліва найбільша цифра (не рахуючи будь-яких провідних нулів, які функціонують лише як заповнювачі і ніколи не є значущими цифрами).
- Якщо округлення до n значущих цифр, то найменш значуща цифра - це n -я цифра з найбільш значущої цифри. Найменш значущою цифрою може бути нуль.
- Перша незначуща цифра - n +1 та цифра.
Правила округлення
- Якщо перша незначна цифра менше 5, то найменш значуща цифра залишається незмінною.
- Якщо перша незначуща цифра більше 5, найменш значуща цифра збільшується на 1.
- Якщо перша незначуща цифра дорівнює 5, найменш значущу цифру можна або збільшити, або залишити без змін (див. Нижче! )
- Всі незначущі цифри прибираються.
Фантазії про п'ятірки
Студентам іноді кажуть збільшити найменш значущу цифру на 1, якщо вона непарна, і залишити її незмінною, якщо вона парна. Хтось задається питанням, чи відображає це деяку думку про те, що парні числа якось «краще», ніж непарні! (Стародавнє забобони якраз навпаки, що тільки непарні числа «пощастило».)
Насправді, ви могли б зробити це однаково навпаки, збільшуючи лише парні числа. Якщо ви округляєте лише одне число, це не має значення, що ви робите. Однак, коли ви округлюєте ряд чисел, які будуть використані в обчисленні, якщо ви обробляєте кожне перше незначне 5 таким же чином, ви будете перевищувати або занижувати значення округленого числа, таким чином накопичуючи помилку округлення. Оскільки є рівні числа парних і непарних цифр, збільшення тільки одного виду буде тримати такого роду помилки від нарощування. Ви могли б зробити так само добре, звичайно, гортаючи монету!
|
число для округлення
|
кількість значущих цифр |
результат
|
коментар
|
|---|---|---|---|
| 34.216 | 3 | 34.2 | Перша незначуща цифра (1) менше 5, тому число просто обрізається. |
| 2.252 | 2 | 2.2 або 2.3 | Перша незначуща цифра дорівнює 5, тому найменший знак. Цифра може або залишитися незмінною, або збільшуватися. |
| 39.99 | 3 | 40.0 | Перетин «десяткової межі», тому всі числа змінюються. |
| 85 381 | 3 | 85,4 00 | Два нулі - це просто заповнювачі |
| 0.04597 | 3 | 0.0460 | Два провідних нулі не є значущими цифрами. |
Округлення дев'яток
Припустимо, що об'єкт має вагу 3,98 ± 0,05 м Це поставило б його справжню вагу десь в діапазоні від 3,93 г до 4,03 м Судячи про те, як округлити це число, ви підраховуєте кількість цифр в «3.98», які точно відомі, і ви не знайдете жодної! Оскільки «4» є лівою найбільшою цифрою, значення якої невизначене, це означало б, що результат повинен бути округлений до однієї значущої цифри і повідомляється просто як 4 м Альтернативою було б зігнути правило і округлити до двох значущих цифр, даючи 4,0 м Як ви можете вирішити, що робити? У такому випадку слід поглянути на неявні невизначеності в двох значеннях та порівняти їх з невизначеністю, пов'язаною з початковим вимірюванням.
|
округлене значення
|
мається на увазі макс
|
мається на увазі хв
|
абсолютна невизначеність
|
відносна невизначеність
|
|---|---|---|---|---|
| 3,98 г | 3,985 г | 3,975 г | ± 0,005 г або 0,01 г | 1 в 400, або 0,25% |
| 4 г | 4,5 г | 3,5 г | ± 0,5 г або 1 г | 1 на 4, 25% |
| 4,0 г | 4,05 г | 3,95 г | ± 0,05 г або 0,1 г | 1 з 40, 2,5% |
Зрозуміло, що округлення до двох цифр є єдиним розумним курсом у цьому прикладі. Спостережувані значення слід округлити до кількості цифр, що найбільш точно передає невизначеність при вимірюванні.
- Зазвичай це означає округлення до кількості значущих цифр в кількості; тобто кількість цифр (рахуючи зліва), які точно відомі, плюс ще одну.
- Коли це не може бути застосовано (як у прикладі вище при додаванні віднімання мостів абсолютної невизначеності на ступінь десяти), то ми округляємо таким чином, щоб відносна мається на увазі невизначеність в результаті була максимально наближеною до спостережуваного значення.
Округлення результатів розрахунків
При проведенні розрахунків, які передбачають кілька кроків, слід уникати будь-яких заокруглень, поки не отримаєте кінцевий результат. Припустимо, ви використовуєте свій калькулятор для опрацювання площі прямокутника:

|
округлене значення
|
відносна мається на увазі невизначеність
|
|---|---|
| 1.58 | 1 частина в 158, або 0,6% |
| 1.6 | 1 частина в 16, або 6% |
Ваш калькулятор, звичайно, правильний, наскільки чисті цифри йдуть, але ви були б неправильно записати «1.57676 см 2" як відповідь. Два можливих варіанти округлення відповіді калькулятора показані праворуч.
Зрозуміло, що жоден варіант не є цілком задовільним; округлення до 3 значущих цифр завищує точність відповіді, тоді як дотримання правила та округлення до двох цифр у «.42» призводить до викидання певної точності. У цьому випадку можна стверджувати, що округлення до трьох цифр виправдано, оскільки мається на увазі відносна невизначеність у відповіді, 0,6%, більше відповідає показникам двох факторів.
«Правила» округлення - це взагалі корисні, зручні орієнтири, але вони не завжди дають найбажаніший результат. Якщо ви сумніваєтеся, краще покладатися на відносні мається на увазі невизначеності.
Додавання і віднімання
При операціях, що включають значні цифри, відповідь повідомляється таким чином, що він відображає надійність найменш точної операції. Відповідь не є більш точною, що найменш точне число використовується для отримання відповіді. При додаванні або відніманні ми йдемо за кількістю знаків після коми (тобто кількістю цифр в правій частині десяткової крапки), а не за кількістю значущих цифр. Визначте кількість, що має найменшу кількість десяткових знаків, і використовуйте це число, щоб встановити кількість десяткових знаків у відповіді.

Множення і ділення
Результат повинен містити таку ж кількість значущих цифр, що і в значенні, що має найменшу кількість значущих цифр.

Логарифми та антилогарифми
Якщо число виражається у вигляді a × 10 b («наукове позначення») з додатковим обмеженням, що коефіцієнт а не менше 1 і менше 10, число знаходиться в нормованому вигляді. Висловіть логарифм базису-10 значення, використовуючи ту ж кількість значущих цифр, що і присутня в нормованому вигляді цього значення. Аналогічно, для антилогарифмів (чисел, виражених у вигляді степеней 10) використовуйте таку ж кількість значущих цифр, що і в цій владі.
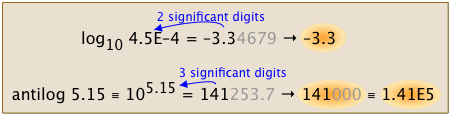
Наступні приклади проілюструють найпоширеніші проблеми, з якими ви, швидше за все, зіткнетеся при округленні результатів розрахунків. Вони заслуговують вашого ретельного вивчення!
|
калькулятор результат |
округлі | зауваження |
|---|---|---|
 |
1.6 | Округлення до двох значущих цифр дає неявну невизначеність 1/16 або 6%, що втричі більше, ніж у найменш точно відомому факторі. Це хороша ілюстрація того, як округлення може призвести до втрати інформації. |
 |
1,9 Е6 | Коефіцієнт «3.1» вказується на 1 частину в 31, або 3%. У відповіді 1.9 значення виражається до 1 частини в 19, або 5%. Ці точності можна порівняти, тому правило округлення дало нам розумний результат. |
|
Певна книга має товщину 117 мм; знайти висоту стопки з 24 однакових книг:
|
281 0 мм | «24» і «1» точні, тому єдиним невизначеним значенням є товщина кожної книги, задана 3 значущими цифрами. Закінчуючий нуль у відповіді є лише заповнювачем. |
 |
10.4 | Крім того, або віднімання шукайте термін, який має найменшу кількість десяткових знаків, і округляйте відповідь на таку ж кількість знаків. |
 |
||
| 23 см | див. нижче |
Останній з наведених вище прикладів являє собою дуже поширену операцію перетворення однієї одиниці в іншу. Тут існує певна кількість неоднозначності; якщо взяти «9 дюймів», щоб означати відстань в діапазоні від 8,5 до 9,5 дюймів, то мається на увазі невизначеність ± 0,5 дюйма, що становить 1 частина в 18, або близько ± 6%. Відносна невизначеність у відповіді повинна бути однаковою, так як всі значення множаться на один і той же коефіцієнт, 2,54 см/дюйм. У цьому випадку ми виправдовуємося в написанні відповіді на дві значущі цифри, що дають невизначеність близько ± 1 см; якби ми використовували відповідь «20 см» (одна значна цифра), то її незрозумілість становила б ± 5 см, або ± 25%.
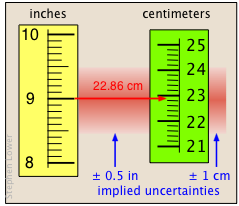
Коли відповідна кількість значущих цифр знаходиться під питанням, обчислення відносної невизначеності може допомогти вам вирішити.

