3.4: Надійність вимірювання
- Page ID
- 19329
- Поясніть різницю між середнім значенням серії вимірювань і середнім чисельністю населення.
- Яка кількість крім середнього значення нам потрібна для того, щоб оцінити якість серії вимірювань?
- Поясніть значення і значення дисперсії середнього, і вкажіть, який фактор контролює його.
- Поясніть різницю між детермінантною та невизначеною помилкою.
- Опишіть призначення процесу використання заготовки і контрольної величини при проведенні ряду вимірювань. Яке принципове припущення має бути зроблено при цьому?
У цей день масової інформації нас постійно бомбардують даними різного роду - опитування громадської думки, рекламний ажіотаж, урядові звіти та заяви політиків. Дуже часто продавці цієї інформації сподіваються «продати» нам товар, ідею чи спосіб мислення про когось чи щось, і при цьому вони занадто часто готові скористатися нездатністю середньостатистичної людини робити обґрунтовані судження про достовірність даних, особливо коли він представлений в певному контексті (в народі відомий як «спина».) У Science у нас немає такої можливості: ми збираємо дані та проводимо вимірювання, щоб наблизитися до будь-якої «правди», яку ми шукаємо, але насправді це не «наука», поки інші не зможуть мати впевненість у достовірності наших вимірювань.
Атрибути вимірювання
Види вимірювань, з якими ми тут будемо займатися, - це ті, при яких проводиться ряд окремих спостережень за окремими зразками, взятими з більшої популяції.
Населення при використанні в статистичному контексті не обов'язково відноситься до людей, а скоріше до сукупності всіх членів даної групи об'єктів.
Наприклад, ви можете визначити кількість нікотину у виробничому циклі мільйона сигарет. Оскільки жодна дві сигарети, швидше за все, не будуть точно однаковими, і навіть якби вони були, випадкова помилка призведе до того, що кожен аналіз дасть інший результат, найкраще, що ви можете зробити, це перевірити репрезентативний зразок, скажімо, двадцять-сто сигарет. Ви берете середнє значення (середнє) цих значень, а потім стикаєтеся з необхідністю оцінити, наскільки точно це вибіркове середнє, ймовірно, наблизить середнє значення популяції. Останнє є «справжньою цінністю», яку ми ніколи не можемо знати; однак, що ми можемо зробити, - це зробити розумну оцінку ймовірності того, що середнє значення вибірки не відрізняється від середнього значення населення більш ніж на певну суму.
Атрибути, які ми можемо призначити окремому набору вимірювань деякої кількості x всередині популяції, наведені нижче. Важливо, щоб ви дізналися значення цих термінів:
Кількість вимірювань
Ця величина зазвичай представлена n.
Середнє
Середнє значення x m (широко відоме як середнє значення), визначене як
Медіана
Медіана значення, з яким ми не будемо мати справу в цій короткій презентації, по суті є тією, що знаходиться в середині списку, що виникає в результаті написання окремих значень в порядку збільшення або зменшення величини.
Діапазон
Діапазон - це різниця між найбільшим і найменшим значенням у множині.
Приклад проблеми:
Знайдіть середнє значення і діапазон набору вимірювань, зображених тут.
Рішення: Цей набір містить 8 вимірювань. Діапазон дорівнює
(10,7 - 10,3) = 0,4, а середнє значення дорівнює
6 Більше однієї відповіді: дисперсія середнього
«Дисперсія» означає «розкиданість». Якщо зробити кілька вимірів і усереднити їх, то вийде певне значення для середнього. Але якщо зробити ще один набір вимірювань, середнє значення цих, швидше за все, буде іншим. Чим більше різниця між засобами, тим більше їх дисперсія.
Припустимо, що замість того, щоб робити п'ять вимірювань, як у наведеному вище прикладі, ми зробили лише два спостереження, які випадково дали значення, які тут виділені. Це призведе до вибіркового середнього значення 10.45. Звичайно, будь-яка кількість інших пар значень могла однаково добре спостерігатися, включаючи множинні випадки будь-якого одного значення, наприклад 10.6.
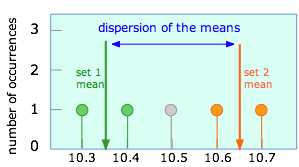Ліворуч показані результати двох можливих пар спостережень, кожна з яких породжує своє середнє значення зразка. Припускаючи, що всі спостереження піддаються лише випадковій помилці, легко помітити, що послідовні пари експериментів можуть дати багато інших вибіркових засобів. Діапазон можливих засобів вибірки відомий як дисперсія середнього.
Зрозуміло, що обидва вибіркові засоби не можуть відповідати середньому населенню, цінність якого ми дійсно намагаємося виявити. Насправді, цілком імовірно, що жоден зразок не є «правильним» у цьому сенсі. Це фундаментальний принцип статистики, однак, що чим більше спостережень ми зробимо, щоб отримати середнє значення вибірки, тим меншим буде дисперсія вибіркових засобів, що є результатом повторюваних множин однакової кількості спостережень. (Це важливо; будь ласка, прочитайте попереднє речення принаймні три рази, щоб переконатися, що ви це розумієте!)
Як дисперсія середнього залежить від кількості спостережень
Різниця між середнім вибірковим (синім) і середнім чисельністю населення («істинне значення», зелений) є похибкою вимірювання. Зрозуміло, що ця помилка зменшується, оскільки кількість спостережень робиться більшою.
Те, що зазначено вище, - це лише ще один спосіб сказати те, що ви, мабуть, вже знаєте: більші зразки дають більш надійні результати. Це той самий принцип, який говорить нам, що перегортання монети 100 разів швидше дасть співвідношення голів до хвостів 50:50, ніж буде знайдено, якщо буде зроблено лише десять сальто (спостережень).
Причиною цього зворотного зв'язку між розміром вибірки та дисперсією середнього є те, що якщо фактори, що породжують різні спостережувані значення, справді випадкові, то чим більше зразків ми спостерігаємо, тим більша ймовірність скасування цих помилок. Виявляється, якщо помилки дійсно випадкові, то, коли ви будуєте кількість входжень кожного значення, результати починають простежувати дуже особливий вид кривої.
Значення цього набагато більше, ніж ви могли б спочатку подумати, тому що G aussian крива має особливі математичні властивості, які ми можемо використовувати за допомогою методів статистики, щоб отримати дуже корисну інформацію про достовірність наших даних. Це і буде головною темою наступного уроку в цьому наборі.
Наразі, однак, нам потрібно встановити деякі важливі принципи щодо похибки вимірювання.
7 Систематична помилка
Розкид у виміряних результатах, які ми обговорювали, виникає внаслідок випадкових варіацій безлічі подій, які впливають на спостережуване значення, і над якими експериментатор не має або обмежений контроль. Якщо ми намагаємося визначити властивості сукупності предметів (вміст нікотину сигарет або термін служби лампових лампочок), то випадкові коливання між окремими членами населення є постійно присутнім фактором. Цей тип помилки називається випадковою або невизначеною помилкою, і це єдиний вид, з яким ми можемо мати справу безпосередньо за допомогою статистики.
Існує, однак, інший тип помилки, який може вплинути на процес вимірювання. Вона відома як систематична або визначальна помилка, і її наслідком є зміщення цілого набору точок даних на постійну величину. Систематична помилка, на відміну від випадкової помилки, не проявляється в самих даних, і її потрібно явно шукати при проектуванні експерименту.
Одним із поширених джерел систематичної помилки є невикористання надійної вимірювальної шкали або неправильне прочитання шкали. Наприклад, ви можете вимірювати довжину предмета за допомогою лінійки, лівий кінець якої зношений, або ви можете неправильно прочитати об'єм рідини в бюретці, дивлячись на верхню частину меніска, а не на його дно, або не маючи рівень очей з об'єктом, що розглядається проти шкали, таким чином, вводячи помилка паралакса.
8 Прогалини та елементи управління
Багато видів вимірювань виробляються приладами, які виробляють реакцію якогось виду (часто електричного струму), прямо пропорційного вимірюваної величині. Наприклад, ви можете визначити кількість розчиненого заліза в розчині, додавши реагент, який реагує з залізом, щоб дати червоний колір, який ви вимірюєте, спостерігаючи інтенсивність зеленого світла, що проходить через фіксовану товщину розчину. У такому випадку, як цей, звичайною практикою є проведення двох додаткових видів вимірювань:
Одне вимірювання робиться на розчині, максимально схожому з невідомими, за винятком того, що він взагалі не містить заліза. Цей зразок називається бланком. Ви налаштовуєте елемент керування на фотометрі, щоб встановити його показання на нуль при вивченні заготовки.
Інше вимірювання проводиться на зразку, що містить відому концентрацію заліза; це зазвичай називають контрольним. Ви регулюєте чутливість фотометра, щоб зробити зчитування деякого довільного значення (50, скажімо) за допомогою контрольного рішення. Припускаючи, що показання фотометра прямо пропорційні концентрації заліза у зразку (це також може бути перевірено, і в цьому випадку повинна бути побудована калібрувальна крива), показання фотометра потім можуть бути перетворені в концентрацію заліза простою пропорцією.
9 Стандартне відхилення
Розглянемо дві пари спостережень, зображених тут:
Зверніть увагу, що зразок означає, що має таке ж значення «40» (чиста удача!) , але різниця в точності двох вимірювань робить очевидним, що набір, показаний праворуч, є більш надійним. Як ми можемо висловити цей факт в стислому вигляді? Можна сказати, що один експеримент дає значення 40 ± 20, а інший 40 ± 5. Хоча ця інформація може бути корисною для деяких цілей, вона не може дати відповідь на такі питання, як «наскільки ймовірно, що інший незалежний набір вимірювань дасть середнє значення в певному діапазоні значень?» Відповідь на це питання, мабуть, є найбільш значущим способом оцінки «якості» або достовірності експериментальних даних, але отримання такої відповіді вимагає використання деякої формальної статистики.
Відхилення від середнього
Ми почнемо з розгляду відмінностей між середнім зразком і окремими значеннями даних, що використовуються для обчислення середнього. Ці відмінності відомі як відхилення від середнього, x i — x m. Ці значення зображені нижче; зверніть увагу, що єдиною відмінністю від графіків вище є розміщення середнього значення при 0 на горизонтальній осі.
Дисперсія і її квадратний корінь
Далі нам потрібно знайти середнє значення цих відхилень. Однак, беручи просте середнє значення, не буде розрізняти ці два конкретні набори даних, оскільки обидва відхилення середні до нуля. Тому ми беремо середнє значення квадратів відхилень (квадратизація змушує зникати ознаки відхилень, щоб вони не могли скасувати). Також обчислюємо середнє, діливши на одиницю менше кількості вимірювань, тобто на n —1, а не на n. Результат, зазвичай позначається S 2, відомий як дисперсія:
Нарешті, візьмемо квадратний корінь дисперсії, щоб отримати стандартне відхилення S:
Приклад завдання: Обчислити дисперсію та стандартне відхилення для кожного з двох наведених вище наборів даних.
Рішення: Заміна на дві формули дає наступні результати:
| значення даних | 20, 60 | 35,45 |
| зразок середнє | 40 | 40 |
| дисперсія S 2 | ||
| стандартне відхилення | 28 | 7.1 |
Коментар: Зверніть увагу, як контрастні значення S відображають різницю в точності двох даних sets— те, що повністю втрачено, якщо тільки два засоби розглядаються.
Тепер, коли ми розробили дуже важливу концепцію стандартного відхилення, ми можемо використовувати її в наступному розділі, щоб відповісти на практичні запитання про те, як інтерпретувати результати вимірювання.
Повернутися до основних фонів для загальної хімії
Повернутися до chem1 (Університет Стівена Лоуер/Саймона Фрейзера)