3.2: Значення міри
- Page ID
- 19328
Переконайтеся, що ви добре розумієте наступні основні ідеї, які були представлені вище. Особливо важливо, щоб ви знали точні значення всіх виділених термінів в контексті даної теми.
- Наведіть приклад вимірюваного числового значення, і поясніть, чим його відрізняє від «чистого» числа.
- Наведіть приклади випадкових і систематичних помилок в вимірах.
- Знайдіть середнє значення ряду аналогічних вимірювань.
- Вкажіть основні фактори, які впливають на різницю між середнім значенням серії вимірювань та «справжнім значенням» вимірюваної величини.
- Обчисліть абсолютну та відносну точність заданого вимірювання та поясніть, чому останнє, як правило, корисніше.
- Розрізняють точність і точність вимірюваного значення, а також за ролями випадкової і систематичної похибки.
Точна відстань між верхньою губою і кінчиком спинного плавника назавжди буде приховано в тумані невизначеності. Кут, під яким ми тримаємо штангенциркуль, і сила, з якою ми їх закриваємо на об'єкті, ніколи не будуть точно відтворюватися. Більш фундаментальне обмеження відбувається кожного разу, коли ми намагаємося порівняти безперервно змінюється величину, таку як відстань з фіксованими інтервалами на вимірювальній шкалі; між 59 і 60 милями існує така ж нескінченність відстаней, яка існує між 59 і 60 милями!
Зображення Стівена Вінсора; використовується з дозволу художника.
«Справжнє значення» виміряної кількості, якщо воно взагалі існує, завжди вислизне від нас; найкраще, що ми можемо зробити, це навчитися змістовно використовувати (і уникати неправильного використання!) чисел, які ми зчитуємо з наших вимірювальних приладів.
Невизначеність певна!
У науці є цифри і є «цифри». Те, що ми зазвичай вважаємо «числом» і будемо називати тут чистим числом саме це: вираз точного значення. Першим з них ви коли-небудь дізналися були підрахунку чисел, або цілих чисел; пізніше, ви були введені в десяткові числа, і раціональні числа, які включають в себе числа, такі як 1/3 і π (pi), які не можуть бути виражені як точні десяткові значення.
Інший вид числової величини, що ми стикаємося в природничих науках є виміряне значення something— довжина або вага об'єкта, обсяг рідини, або, можливо, читання на приладі. Хоча ми виражаємо ці значення чисельно, було б помилкою вважати їх різновидом чистих чисел, описаних вище.
Заплутаний? Припустимо, наш прилад має такий індикатор, який ви бачите тут. Покажчик рухається вгору і вниз таким чином, щоб відобразити виміряне значення на цій шкалі. Яке число ви б написали у своєму блокноті під час запису цього вимірювання? Зрозуміло, що значення десь між 130 і 140 на шкалі, але градуювання дозволяють нам бути більш точними і розмістити значення між 134 і 135. Індикатор більше вказує на останнє значення, і ми можемо піти ще один крок, оцінивши значення, можливо, як 134,8, так що це значення ви б повідомити для цього вимірювання.
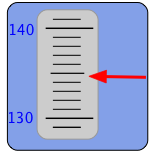
Тепер ось важливо зрозуміти: хоча «134.8» сам по собі є числом, кількість, яку ми вимірюємо, майже напевно не 134.8— принаймні, не точно. Причина очевидна, якщо відзначити, що шкала приладу така, що ми ледве можемо розрізнити між 134,7, 134,8 і 134,9. Повідомляючи значення 134.8, ми фактично говоримо, що значення, ймовірно, десь з діапазоном 134,75 до 134,85. Іншими словами, в нашому вимірі існує невизначеність ± 0,05 одиниці.
Всі вимірювання величин, які можуть припускати безперервний діапазон значень (довжини, маси, обсяги і т.д.) складаються з двох частин: самого звітованого значення (ніколи точно відомого числа), і невизначеності, пов'язаної з вимірюванням. Під «помилкою» ми маємо на увазі не просто відверті помилки, такі як неправильне використання приладу або нездатність правильно прочитати шкалу; хоча такі грубі помилки іноді трапляються, вони зазвичай дають результати, які є досить несподіваними, щоб привернути увагу до себе.
Всі вимірювання схильні до похибки, що сприяє невизначеності результату. Під «помилкою» ми маємо на увазі не просто відверті помилки, такі як неправильне використання приладу або нездатність правильно прочитати шкалу; хоча такі грубі помилки іноді трапляються, вони зазвичай дають результати, які є досить несподіваними, щоб привернути увагу до себе.
Коли ви вимірюєте обсяг або вагу, ви спостерігаєте читання за шкалою якогось виду. Ваги, за своєю природою, обмежуються фіксованими збільшеннями величини, позначеними знаками поділу. Фактичні величини, які ми вимірюємо, навпаки, можуть постійно змінюватися, тому існує властиве обмеження в тому, наскільки тонко ми можемо розрізняти два значення, які потрапляють між позначеними поділами вимірювальної шкали. Та ж проблема залишається, якщо ми підставимо прилад цифровим дисплеєм; завжди буде якась точка, в якій деяке значення, яке лежить між двома найменшими поділами, повинно довільно перемикатися між двома числами на дисплеї зчитування. Це вводить елемент випадковості у значення, яке ми спостерігаємо, навіть якщо значення «true» залишається незмінним.
Чим чутливіший вимірювальний прилад, тим менше ймовірність того, що два послідовних вимірювання одного і того ж зразка дадуть ідентичні результати. У прикладі, про який ми говорили вище, розрізнити значення 134,8 і 134,9 може бути занадто важко зробити послідовно, тому два незалежних спостерігача можуть записувати різні значення навіть при перегляді одного і того ж показання. На кожне вимірювання також впливає безліч незначних подій, таких як коливання будівлі, електричні коливання, рухи повітря та тертя в будь-яких рухомих частинях приладу. Ці крихітні впливи складають своєрідний «шум», який також має випадковий характер. Незалежно від того, усвідомлюємо ми це чи ні, всі виміряні значення містять елемент випадкової помилки.
На кожне вимірювання також впливає безліч незначних подій, таких як коливання будівлі, електричні коливання, рухи повітря та тертя в будь-яких рухомих частинях приладу. Ці крихітні впливи складають своєрідний «шум», який також має випадковий характер. Незалежно від того, усвідомлюємо ми це чи ні, всі виміряні значення містять елемент випадкової помилки.
Припустимо, що ви зважуєтеся на вагах для ванної, не помічаючи, що циферблат читає «1,5 кг» ще до того, як ви поставили на нього свою вагу. Аналогічно, ви можете використовувати стару лінійку зі зношеним кінцем, щоб виміряти довжину шматка дерева. В обох цих прикладах всі наступні вимірювання, або одного об'єкта, або різних, будуть відключені на постійну величину. На відміну від випадкової помилки, яку неможливо усунути, ці систематичні помилки зазвичай досить легко уникнути або компенсувати, але тільки свідомим зусиллям при проведенні спостереження, як правило, шляхом правильного обнулення і калібрування вимірювального приладу. Однак, як тільки систематична помилка знайшла свій шлях до даних, це може бути дуже важко виявити.
Різниця між точністю та точністю
Ми схильні використовувати ці два терміни взаємозамінно в нашій звичайній розмові, але в контексті наукового вимірювання вони мають дуже різні значення:
- Точність відноситься до того, наскільки точно виміряне значення кількості відповідає його «істинному» значенню.
- Точність виражає ступінь відтворюваності, або узгодження між повторними вимірами.
Точність, звичайно, є метою, до якої ми прагнемо в наукових вимірах. На жаль, однак, немає очевидного способу дізнатися, наскільки тісно ми цього досягли; «справжнє» значення, будь то чітко визначена величина, така як маса конкретного об'єкта, або середнє значення, яке стосується колекції предметів, ніколи не може бути відомо - і тому ми ніколи не можемо його розпізнати, якщо ми є пощастило знайти його.
Уважно зауважте, що коли ми робимо реальні вимірювання, немає дошки для дартсу або мішені, яка дозволяє негайно судити про якість результату. Якщо ми зробимо лише кілька спостережень, ми можемо не розрізнити жоден із цих сценаріїв. Таким чином, ми не можемо розрізнити чотири сценарії, проілюстровані вище, просто вивчивши результати двох вимірювань. Однак ми можемо судити про точність результатів, а потім застосувати просту статистику, щоб оцінити, наскільки близько середнє значення, ймовірно, відобразить справжнє значення за відсутності систематичної помилки.
Більше однієї відповіді в Replicate вимірювань
Якщо ви хочете виміряти свій зріст до найближчого сантиметра або дюйма, або обсяг рідкого інгредієнта для приготування їжі до найближчої «чашки», ви, ймовірно, можете зробити це, не турбуючись про випадкову помилку. Помилка все одно буде присутній, але її величина складе таку малу частку від величини, що вона не буде виявлена. Таким чином, випадкова помилка - це не те, про що ми переживаємо занадто багато в нашому повсякденному житті.
Однак якщо ми робимо наукові спостереження, нам потрібно бути обережнішими, особливо якщо ми намагаємося використовувати повну чутливість наших вимірювальних приладів, щоб досягти максимально надійного результату. Якщо ми вимірюємо безпосередньо спостережувану величину, таку як вага або об'єм об'єкта, то одного вимірювання, ретельно зробленого та повідомленого з точністю, яка відповідає точності вимірювального приладу, зазвичай буде достатньо.
Однак частіше нас закликають знайти значення якоїсь величини, визначення якої залежить від кількох інших виміряних значень, кожне з яких піддається власним джерелам похибки. Розглянемо поширений лабораторний експеримент, в якому необхідно визначити відсоток кислоти в пробі оцту, дотримуючись обсяг розчину гідроксиду натрію, необхідний для нейтралізації заданого обсягу оцту. Ви проводите експеримент і отримуєте значення. Тільки щоб бути в безпеці, повторюєте процедуру на іншому ідентичному зразку з тієї ж пляшки оцту. Якщо ви насправді зробили це в лабораторії, ви будете знати, що дуже малоймовірно, що друге випробування дасть той же результат, що і перше. Насправді, якщо ви запустите ряд реплікації (тобто однакових у всіх відношеннях) визначень, ви, ймовірно, отримаєте розкид результатів.
Щоб зрозуміти чому, розглянемо всі індивідуальні вимірювання, які йдуть у кожне визначення; обсяг зразка оцту, ваше судження про точку, в якій оцет нейтралізується, і обсяг розчину, який використовується для досягнення цієї точки. І наскільки точно ви знаєте концентрацію розчину гідроксиду натрію, який був складений шляхом розчинення вимірюваної ваги твердої речовини у воді, а потім додавання більше води, поки розчин не досягне деякого виміряного обсягу. Кожен з цих багатьох спостережень піддається випадковій помилці; оскільки такі помилки є випадковими, вони можуть час від часу скасувати, але для більшості випробувань ми не будемо так lucky— отже, розкид у результатах.
Подібна складність виникає, коли нам потрібно визначити якусь величину, яка описує сукупність предметів. Наприклад, фармацевтичному досліднику потрібно буде визначити час, необхідний для половини стандартної дози певного препарату, який повинен бути виведений організмом, або виробник лампочок може захотіти знати, скільки годин буде працювати певний тип лампочки, перш ніж він згорить. У цих випадках значення для будь-якого окремого зразка можна визначити досить легко, але оскільки немає двох зразків (пацієнтів або лампочок) однакових, ми змушені повторювати одне і те ж вимірювання на декількох зразках, і ще раз стикаємося з розсіюванням результатів.
В якості заключного прикладу припустимо, що ви хочете визначити діаметр певного типу монети. Ви робите одне вимірювання і записуєте результати. Якщо потім зробити подібний вимір уздовж різного перерізу монети, ви, швидше за все, отримаєте інший результат. Те ж саме станеться, якщо провести послідовні виміри на інших монетах такого ж виду.
Тут ми стикаємося з двома видами проблем. По-перше, є властива обмеженість вимірювального приладу: ми ніколи не зможемо достовірно виміряти більш тонко, ніж зазначені поділи на лінійці. По-друге, ми не можемо припустити, що монета ідеально кругова; ретельний огляд, швидше за все, виявить деякі спотворення, спричинені невеликим недосконалістю у процесі виробництва. У цих випадках виходить, що єдиного, істинного значення жодної кількості, яку ми намагаємося виміряти, не існує.
Середнє, медіане та діапазон серії спостережень
Існують різні способи вираження середньої або центральної тенденції ряду вимірювань, причому найчастіше використовується середнє (точніше, середнє арифметичне). Наше звичайне вживання терміна «середній» також відноситься до середнього. Коли ми отримуємо більше одного результату для даного вимірювання (або зроблено повторно на одному зразку, або частіше на різних зразках), найпростішою процедурою є повідомлення про середнє, або середнє значення. Середнє визначається математично як сума значень, розділена на кількість вимірювань:
\[x_m = \dfrac{\displaystyle \sum_i x_i}{n} \label{mean}\]
Якщо ви не знайомі з цим позначенням, не дозволяйте йому лякати вас! Знайдіть хвилинку, щоб побачити, як воно виражає попереднє речення; якщо є\(n\) вимірювання, кожне з яких дає значення xI, то ми підсумовуємо по всьому\(i\) і ділимо на,\(n\) щоб отримати середнє значення\(x_m\). Наприклад, якщо вимірювань всього два,\(x_1\) і\(x_1\), то середнє значення є\((x_1 + x_2)/2\).
Обчисліть середнє значення набору восьми вимірів, проілюстрованих тут.
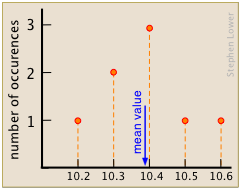
Рішення
Є вісім точок даних (10,4 було знайдено в трьох випробуваннях, 10,5 в двох), так\(n=8\). Середнє значення є (через рівняння\ ref {середнє}):
\[ \dfrac{10.2+10.3+(3 x 10.4) + 10.5+10.5+10.8}{8} = 10.4. \nonumber\]
Діапазон
Діапазон набору даних - це різниця між його найменшими та найбільшими значеннями. Як така його величина відображає точність результату. Наприклад, наступні набори даних мають однакове середнє значення, але той, що має менший діапазон, явно точніше.
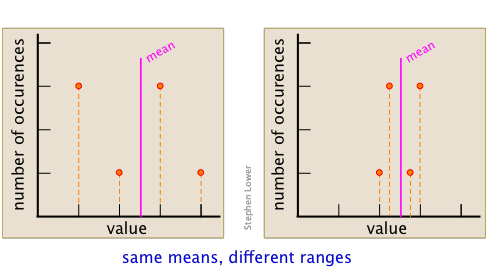
Якщо розташувати список вимірюваних значень в порядку їх величини, медіана - це та, яка має стільки значень над нею, скільки нижче неї.
Приклади: для набору даних [22 23 23 24 26 28] режим буде 23.
Для непарної кількості значень n медіаною є [(n +1) /2] -й член множини. Таким чином, для [22 23 23 24 24 27], (n +1) /2 =3, так 23 - це медіана.
Режим
Мається на увазі значення, яке спостерігається найчастіше в серії вимірювань. Якщо два і більше значення прив'язують для найвищої частоти, то режимів може бути кілька. Режим найбільш корисний при описі великих наборів даних.
Приклад: для набору даних [22 23 23 24 26 26] режими 23 і 24.
Чим більше спостережень, тим достовірніше середнє значення. Якщо це не відразу очевидно, подумайте про це так. Ви б не хотіли прогнозувати результат наступних виборів на основі інтерв'ю лише з двома-трьома виборцями; ви хотіли б вибірку від десяти до двадцяти як мінімум, і якщо вибори є важливими національними, справедлива вибірка вимагатиме від сотень до тисяч людей, розподілених по всьому географічним районом і представляють собою різноманітні соціально-економічні групи. Аналогічно, ви хотіли б перевірити велику кількість лампочок, щоб оцінити середній термін служби лампочок цього типу.
Статистична теорія говорить нам, що чим більше зразків у нас буде, тим більшим буде шанс, що середнє значення результатів буде відповідати «справжньому» значенню, яке в цьому випадку було б середнім, отриманим, якби зразки можна було взяти з усієї популяції (людей або лампочок).
Цей момент можна краще оцінити, вивчивши два набори даних, показані тут. Набір зліва складається всього з трьох точок (показаний помаранчевим кольором), і дає середнє значення, досить далеке від «істинного» значення, яке довільно вибирається для цього прикладу.
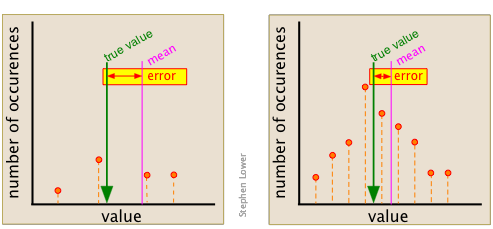
У даних, розташованих праворуч, складеному з дев'яти вимірювань, відхилення середнього від істинного значення значно менше.
Відхилення середнього від «істинного значення» стає менше, коли проводиться більше вимірювань.
Сюжети і точки
Подібна проблема виникає при спробі підігнати криву до ряду нанесених точок. Припустимо, наприклад, що крива 1 (червона) являє собою істинне співвідношення між величинами, зазначеними на осі y (залежна змінна), і величинами на осі x (незалежна змінна). Ця крива виводиться з семи точок, зазначених на ділянці.
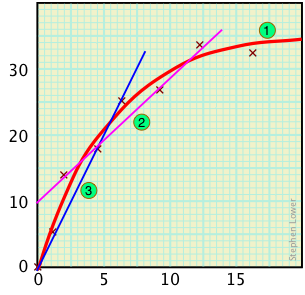
Контраст цієї кривої з помилковими прямими відносинами, які можуть бути отримані, якщо було записано лише чотири або три точки.
Абсолютна і відносна невизначеність
Якщо ви зважуєте 74,1 мг твердого зразка на лабораторних вагах, які з точністю до 0,1 міліграма, то фактична вага зразка, ймовірно, впаде десь в діапазоні від 74,0 до 74,2 мг; абсолютна невизначеність у вазі, яку ви спостерігаєте, становить 0,2 мг, або ± 0,1 мг. Якщо ви використовуєте той самий баланс для зважування 3,2914 г іншого зразка, фактична вага становить від 3,2913 г до 3,2915 г, а абсолютна невизначеність все ще становить ± 0,1 мг. Таким чином, абсолютна невизначеність не пов'язана з величиною спостережуваного значення.
При вираженні невизначеності величини, наведеної в науковому позначенні, експоненціальна частина повинна включати як саму величину, так і невизначеність. Прикладом правильної форми буде (3,19 ± 0,02) × 10 4 м.
Хоча абсолютні невизначеності в цих двох прикладах ідентичні, ми, ймовірно, вважаємо друге вимірювання більш точним, оскільки невизначеність є меншою часткою вимірюваного значення. Кількість, розрахована таким чином, відома як відносна невизначеність.
Обчисліть відносні невизначеності наступних абсолютних невизначеностей:
- 74,1 ± 0,1 мг,
- 3,2914 ± 0,1 мг.
Рішення
- \[\dfrac{0.2\, mg}{74.1\, mg} = 0.0027\, \text{or} \, 0.003 \nonumber\](Зверніть увагу, що частка безрозмірна) це може виражатися як 0,3% (3 частини на сотню) або 3 частини на тисячу.
- \[\dfrac{0.0002 \,g}{3.2913\, g} = 8.4 \times 10^{-5} \, \text{or roughly} \,8 \times 10^{-5} \nonumber\], які ми можемо висловити як\(8 \times 10^{-3}\%\) (0,008 частин на сотню), або (8Е-5/ 10) = 8Е-6 = 8 проміле.
Відносні невизначеності широко використовуються для вираження надійності вимірювань, навіть тих, що для одного спостереження, і в цьому випадку невизначеність є невизначеністю вимірювального приладу. Відносні невизначеності можуть виражатися у вигляді частин на сто (відсотків), на тисячу (PPT), на мільйон, (PPM) і так далі.
Поширення помилки
Нас часто закликають знайти значення якоїсь величини, визначення якої залежить від кількох інших виміряних значень, кожне з яких піддається власним джерелам помилки.
Розглянемо поширений лабораторний експеримент, в якому необхідно визначити відсоток кислоти в пробі оцту, дотримуючись обсяг розчину гідроксиду натрію, необхідний для нейтралізації заданого обсягу оцту. Ви проводите експеримент і отримуєте значення. Тільки щоб бути в безпеці, повторюєте процедуру на іншому ідентичному зразку з тієї ж пляшки оцту. Якщо ви насправді зробили це в лабораторії, ви будете знати, що дуже малоймовірно, що друге випробування дасть той же результат, що і перше. Насправді, якщо ви запустите ряд реплікації (тобто однакових у всіх відношеннях) визначень, ви, ймовірно, отримаєте розкид результатів.
Щоб зрозуміти чому, розглянемо всі індивідуальні вимірювання, які йдуть в кожне визначення; обсяг зразка оцту, ваше судження про точку, в якій оцет нейтралізується, і обсяг розчину, який використовується для досягнення цієї точки. І наскільки точно ви знаєте концентрацію розчину гідроксиду натрію, який був складений шляхом розчинення вимірюваної ваги твердої речовини у воді, а потім додавання більше води, поки розчин не досягне деякого виміряного обсягу. Кожне з цих численних спостережень піддається випадковій помилці; оскільки такі помилки є випадковими, вони іноді можуть скасовуватися, але для більшості випробувань нам не пощастить - звідси і розкид результатів.
Правила оцінки похибок в розрахункових результатах
Припустимо, ви вимірюєте масу і обсяг зразка, і зобов'язані обчислити його щільність, розділивши одну величину на іншу: d = m/V. Обидві складові цього частки мають невизначеності, пов'язані з ними, і ви хочете додати невизначеність до розрахункової щільності. Загальна проблема визначення невизначеності розрахункового результату виявляється досить складною, ніж ви могли б подумати, і тут розглядатися не буде. Є, однак, деякі дуже прості правила, яких достатньо для більшості практичних цілей.
- Додавання та віднімання, обидва числа мають невизначеність: Найпростіший метод - просто додати абсолютну невизначеність.
- Множення або ділення, обидва числа мають невизначеності: Перетворіть абсолютні невизначеності у відносні невизначеності та додайте їх. Або краще, складіть їх квадрати і візьміть квадратний корінь від суми.
- Множення або ділення на чисте число: Тривіальний випадок; помножити або розділити невизначеність на чисте число.
\[(6.3 ± 0.05 cm) – (2.1 ± 0.05 cm) = 4.2 ± 0.10 cm\]
Однак це, як правило, переоцінює невизначеність, припускаючи найгірший можливий випадок, коли помилка в одній із величин знаходиться на максимальному позитивному значенні, тоді як помилка іншої кількості - на максимальному мінімальному значенні.
Статистична теорія повідомляє нам, що більш реалістичне значення невизначеності суми або різниці полягає в тому, щоб скласти квадрати кожної абсолютної невизначеності, а потім взяти квадратний корінь цієї суми. Застосовуючи це до вищевказаних значень, ми маємо
\[\sqrt{(0.05)^2 + (0.05)^2} = 0.07\]
так результат становить 4,2 ± 0,07 см.
Оцініть абсолютну похибку щільності, розраховану діленням (12,7 ± 0,05 г) на (10,0 ± 0,02 мл).
Рішення
Відносна невизначеність маси:
\[\dfrac{0.05}{12.7} = 0.0039 = 0.39\% \nonumber\]
Відносна невизначеність обсягу:
\[\dfrac{0.02}{10.0} = 0.002 = 0.2\% \nonumber\]
Відносна невизначеність щільності:
\[ \sqrt{ (0.39)^2 + (0.2)^2} = 0.44 \% \nonumber\]
Маса ÷ об'єм:
\[(12.7\, g) ÷ (10.0 \,mL) = 1.27 \,g \,mL^{–1} \nonumber \]
Абсолютна невизначеність щільності:
\[(± 0.044) \times (1.27 \,g \,mL^{–1}) = ±0.06\, g\, mL^{–1} \nonumber \]
