2.4: Значення міри

Цілі навчання

• Наведіть приклад вимірюваного числового значення, і поясніть, чим його відрізняє від «чистого» числа.
• Наведіть приклади випадкових і систематичних помилок в вимірах.
• Знайдіть середнє значення ряду аналогічних вимірювань.
• Вкажіть основні фактори, які впливають на різницю між середнім значенням серії вимірювань та «справжнім значенням» вимірюваної величини.
• Обчисліть абсолютну та відносну точність заданого вимірювання та поясніть, чому останнє, як правило, корисніше.
• Розрізняють точність і точність вимірюваного значення, а також за ролями випадкової і систематичної похибки.

У науці є цифри і є «цифри». Те, що ми зазвичай вважаємо «числом» і будемо називати тут чистим числом саме це: вираз точного значення. Першим з них ви коли-небудь дізналися були підрахунку чисел, або цілих чисел; пізніше, ви були введені в десяткові числа, і раціональні числа, які включають в себе числа, такі як 1/3 і π (pi), які не можуть бути виражені як точні десяткові значення. Інший вид числової величини, що ми стикаємося в природничих науках є виміряне значення something— довжина або вага об'єкта, обсяг рідини, або, можливо, читання на приладі. Хоча ми виражаємо ці значення чисельно, було б помилкою вважати їх різновидом чистих чисел, описаних вище.

Заплутаний? Припустимо, наш прилад має такий індикатор, який ви бачите тут. Покажчик рухається вгору і вниз таким чином, щоб відобразити виміряне значення на цій шкалі. Яке число ви б написали у своєму блокноті під час запису цього вимірювання? Зрозуміло, що значення десь між 130 і 140 на шкалі, але градуювання дозволяють нам бути більш точними і розмістити значення між 134 і 135. Індикатор більше вказує на останнє значення, і ми можемо піти ще один крок, оцінивши значення, можливо, як 134,8, так що це значення ви б повідомити для цього вимірювання.

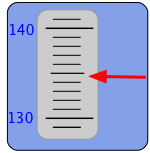
Тепер важливо зрозуміти: хоча «134.8» є числом, кількість, яку ми вимірюємо, майже напевно не 134,8 - принаймні, не зовсім. Причина очевидна, якщо зауважити, що шкала приладу така, що ми ледве можемо розрізнити між 134,7, 134,8 і 134,9. Повідомляючи значення 134.8, ми фактично говоримо, що значення, ймовірно, десь з діапазоном 134,75 до 134,85. Іншими словами, в нашому вимірі існує невизначеність ± 0,05 одиниці.

Всі вимірювання величин, які можуть припускати безперервний діапазон значень (довжини, маси, обсяги і т.д.) складаються з двох частин: самого звітованого значення (ніколи точно відомого числа), і невизначеності, пов'язаної з вимірюванням. Під «помилкою» ми маємо на увазі не просто відверті помилки, такі як неправильне використання приладу або нездатність правильно прочитати шкалу; хоча такі грубі помилки іноді трапляються, вони зазвичай дають результати, які є досить несподіваними, щоб привернути увагу до себе.

Помилка зчитування масштабу

Коли ви вимірюєте об'єм або вагу, ви спостерігаєте читання за певною шкалою, наприклад, проілюстрованою вище. Ваги, за своєю природою, обмежуються фіксованими збільшеннями величини, позначеними знаками поділу. Фактичні величини, які ми вимірюємо, навпаки, можуть постійно змінюватися, тому існує властиве обмеження в тому, наскільки тонко ми можемо розрізняти два значення, які потрапляють між позначеними поділами вимірювальної шкали. Помилка масштабування читання часто класифікується як випадкова помилка (див. Нижче), але вона зустрічається настільки часто, що ми розглядаємо її окремо тут.

Та ж проблема залишається, якщо ми підставимо прилад цифровим дисплеєм; завжди буде точка, в якій деяке значення, яке лежить між двома найменшими поділами, повинно довільно перемикатися між двома числами на дисплеї зчитування. Це вводить елемент випадковості у значення, яке ми спостерігаємо, навіть якщо значення «true» залишається незмінним. Чим чутливіший вимірювальний прилад, тим менше ймовірність того, що два послідовних вимірювання одного і того ж зразка дадуть ідентичні результати. У прикладі, про який ми говорили вище, розрізнити значення 134,8 і 134,9 може бути занадто важко зробити послідовно, тому два незалежних спостерігача можуть записувати різні значення навіть при перегляді одного і того ж показання.

Помилка паралакса

Однією з форм помилки читання масштабу, яка часто страждає початківців у науковій лабораторії, є нездатність належним чином вирівняти око з частиною шкали, яку ви читаєте. Це призводить до помилки паралакса. Паралакс відноситься до зміни видимого положення об'єкта при погляді з різних точок.

Найбільш горезвісний приклад, який зустрічається у вступній хімічній лабораторії, - це нездатність правильно прочитати обсяг рідини в градуйованому циліндрі або бюретці. Навчання всіх своїх студентів, щоб переконатися, що їхнє око знаходиться на рівні з дном меніска - це надія та відчай інструкторів лабораторії.

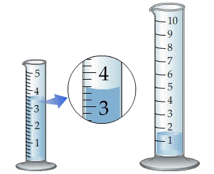
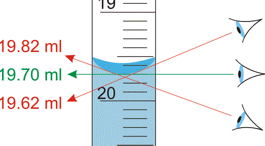
Правильне використання вимірювального приладу може допомогти зменшити ймовірність помилки паралакса. Наприклад, шкала довжини повинна знаходитися в безпосередньому контакті з об'єктом (зліва), а не над ним, як праворуч.

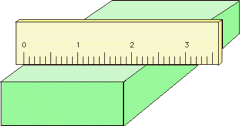
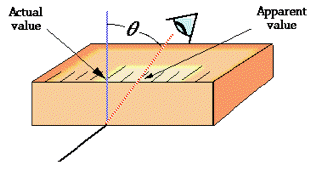
Аналогові лічильники (ті, що мають стрілкові голки) є найбільш точними при зчитуванні приблизно на 2/3 довжини шкали. Вимірювачі аналогового типу, на відміну від тих, що мають цифрові зчитування, також схильні до помилки паралакса. Ті, що призначені для високоточних застосувань, часто мають дзеркальну дугу вздовж шкали, в якій можна побачити відображення стрілки вказівника, якщо глядач неправильно вирівняний з інструментом.

• Випадкова (невизначена) похибка: На кожне вимірювання також впливає безліч незначних подій, таких як коливання будівлі, електричні коливання, рухи повітря та тертя в будь-яких рухомих частинях приладу. Ці крихітні впливи складають своєрідний «шум», який також має випадковий характер. Незалежно від того, усвідомлюємо ми це чи ні, всі виміряні значення містять елемент випадкової помилки.
• Систематична помилка: Припустимо, що ви зважуєтеся на вагах для ванної, не помічаючи, що циферблат читає «1,5 кг» ще до того, як ви поставили на нього свою вагу. Аналогічно, ви можете використовувати стару лінійку зі зношеним кінцем, щоб виміряти довжину шматка дерева. В обох цих прикладах всі наступні вимірювання, або одного і того ж об'єкта, або різних, будуть відключені на постійну величину. На відміну від випадкової помилки, яку неможливо усунути, ці систематичні помилки (також відомі як визначальна помилка), як правило, досить легко уникнути або компенсувати, але лише свідомими зусиллями при проведенні спостереження, як правило, шляхом належного обнулення та калібрування вимірювання інструмент. Однак, як тільки систематична помилка знайшла свій шлях до даних, це може бути дуже важко виявити.

Точність і точність

Ми схильні використовувати ці два терміни взаємозамінно в нашій звичайній розмові, але в контексті наукового вимірювання вони мають дуже різні значення:

• Точність відноситься до того, наскільки точно виміряне значення кількості відповідає його «істинному» значенню.
• Точність виражає ступінь відтворюваності, або узгодження між повторними вимірами.

Точність, звичайно, є метою, до якої ми прагнемо в наукових вимірах. На жаль, однак, немає очевидного способу дізнатися, наскільки тісно ми цього досягли; «справжнє» значення, будь то чітко визначена величина, така як маса конкретного об'єкта, або середнє значення, яке стосується колекції предметів, ніколи не може бути відоме - і тому ми ніколи не можемо його розпізнати, якщо ми пощастило знайти його.

Чотири сценарії

Мішень на дротиках служить зручною аналогією. Результати чотирьох наборів вимірювань (або чотирьох ігор в дартс) проілюстровані нижче. Кожен набір складається з десяти спостережень (або кидків дротиків). Кожна червона точка відповідає точці, в якій дротик потрапив у ціль, або, альтернативно, значенню окремого спостереження. Для вимірювань припустимо, що справжнє значення вимірюваної величини лежить в центрі кожної мети. Тепер розглянемо наступні чотири набори результатів:

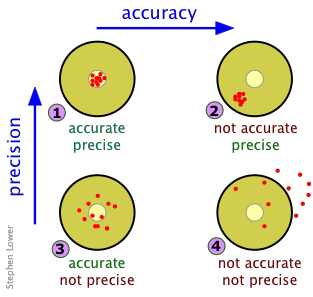
Прямо на! Ви виграєте гру в дартс і отримуєте оцінку А за результатами вимірювань.

Ваші результати чудово відтворюються, але ваш вимірювальний прилад, можливо, не був відкалібрований належним чином або ваші спостереження страждають від систематичної помилки якогось роду. Точність: F, Precision, A; загальний клас C.

Надзвичайно малоймовірно, і, ймовірно, через чисту удачу; єдина причина точного означає, що ваші промахи в основному скасовані. Сорт D.

Досить сумно; подумайте про перехід на музику чи політику - або огляньте ваші очі.

Примітка

Коли ми робимо реальні вимірювання, немає дошки для дартсу або мішені, яка дозволяє негайно судити про якість результату. Якщо ми зробимо лише кілька спостережень, ми можемо не розрізнити жоден із цих сценаріїв.

«Справжнє значення» бажаного вимірювання може бути досить невловимим і навіть не може бути визначено взагалі. Це дуже поширена складність як в соціальних науках (як в соціологічних опитуваннях), в медицині (оцінка ефективності препарату або іншого лікування), так і у всіх інших природничих науках. Правильне лікування таких проблем полягає в тому, щоб зробити кілька спостережень окремих випадків того, що вимірюється, а потім використовувати статистичні методи для оцінки результатів. У цій вступній одиниці вимірювання ми відкладемо обговорення таких понять, як стандартне відхилення та довірчі інтервали, які стають важливими на курсах на рівні другого року та за його межами. Ми обмежимо наше лікування тут елементарними міркуваннями, які, ймовірно, знадобляться в типовому курсі першого року.

Скільки вимірювань мені потрібно?

Одного вимірювання може бути достатньо. Якщо ви хочете виміряти свій зріст до найближчого сантиметра або дюйма, або обсяг рідкого інгредієнта для приготування їжі до найближчої 1/8 «чашки», ви зазвичай не турбуєтеся про випадкову помилку. Похибка все одно буде присутній, але її величина складе таку малу частку від величини, що вона істотно не вплине на те, чого ми намагаємося досягти. Таким чином, випадкова помилка - це не те, про що ми стурбовані в нашому повсякденному житті. У науковій лабораторії існує багато контекстів, в яких єдине спостереження за обсягом, масою або читанням приладу має сенс; частина «мистецтва» науки полягає у прийнятті усвідомленого судження про те, наскільки точним має бути дане вимірювання. Якщо ми вимірюємо безпосередньо спостережувану величину, таку як вага твердої речовини або об'єм рідини, то одноразового вимірювання, ретельно зробленого та повідомленого з точністю, яка відповідає точності вимірювального приладу, зазвичай буде достатньо.

Однак потрібні додаткові вимірювання, коли немає чітко визначеного «істинного» значення. Колекція предметів (або людей) відома в статистиці як населення. Часто виникає необхідність визначити якусь величину, яка описує колекцію об'єктів. Наприклад, фармацевтичному досліднику потрібно буде визначити час, необхідний для половини стандартної дози певного препарату, який повинен бути виведений організмом, або виробник лампочок може захотіти знати, скільки годин буде працювати певний тип лампочки, перш ніж він згорить. У цих випадках значення для будь-якого окремого зразка можна визначити досить легко, але оскільки немає двох зразків (пацієнтів або лампочок) однакових, ми змушені повторювати одне і те ж вимірювання на декількох об'єктах. І природно, ми отримуємо різноманітні результати, зазвичай іменовані розкидом. Навіть для окремого об'єкта може не бути чітко визначеного «істинного» значення.

Припустимо, що ви бажаєте визначити діаметр певного виду монети. Ви робите одне вимірювання і записуєте результати. Якщо потім зробити подібний вимір уздовж різного перерізу монети, ви, швидше за все, отримаєте інший результат. Те ж саме станеться, якщо провести послідовні виміри на інших монетах такого ж виду.

Тут ми стикаємося з двома видами проблем. По-перше, є властива обмеженість вимірювального приладу: ми ніколи не зможемо достовірно виміряти більш тонко, ніж зазначені поділи на лінійці. По-друге, ми не можемо припустити, що монета ідеально кругова; ретельний огляд, швидше за все, виявить деякі спотворення, спричинені невеликим недосконалістю у процесі виробництва. У цих випадках виходить, що єдиного, істинного значення кількості, яку ми намагаємося виміряти, не існує.

Середнє, медіана та діапазон ряду спостережень

Існує безліч способів виразити середню, або центральну тенденцію ряду вимірювань, причому найчастіше використовується середнє (точніше, середнє арифметичне). Наше звичайне вживання терміна «середній» також відноситься до середнього. Ці поняття, як правило, все, що вам потрібно в якості першого кроку в аналізі даних, які ви, ймовірно, збираєте на першому курсі хімії лабораторії.

Середнє значення і його значення

У нашій звичайній мові термін «середній» є синонімом «середнє». У статистиці, однак, «середній» - це більш загальний термін, який може стосуватися медіани, режиму та діапазону, а також означати. Коли ми отримуємо більше одного результату для даного вимірювання (або зробленого повторно на одному зразку, або частіше, на різних зразках одного і того ж матеріалу), найпростішою процедурою є повідомлення про середнє, або середнє значення. Середнє визначається математично як сума значень, розділена на кількість вимірювань:

\[ x_m = \dfrac{\sum_{i=1}^n x_i}{n}\]

Якщо ви не знайомі з цим позначенням, не дозволяйте йому лякати вас! Це нічим не відрізняється від середнього, з яким ви, швидше за все, вже знайомі. Знайдіть хвилинку, щоб побачити, як воно виражає попереднє речення; якщо є\(n\) вимірювання, кожне з яких дає значення xi, то ми підсумовуємо по всьому\(i\) і ділимо на,\(n\) щоб отримати середнє значення\(x_m\). Наприклад, якщо вимірювань всього два, х ₁ і х ₁, то середнє значення

\[ x_m = \dfrac{x_1 + x_2}{2}\]

Загальна проблема визначення невизначеності розрахункового результату виявляється досить складною, ніж ви могли б подумати, і тут розглядатися не буде. Є, однак, деякі дуже прості правила, яких достатньо для більшості практичних цілей.

Абсолютна і відносна невизначеність

Якщо ви зважуєте 74,1 мг твердого зразка на лабораторних вагах, які з точністю до 0,1 міліграма, то фактична вага зразка, ймовірно, впаде десь в діапазоні від 74,0 до 74,2 мг; абсолютна невизначеність у вазі, яку ви спостерігаєте, становить 0,2 мг, або ± 0,1 мг. Якщо ви використовуєте той самий баланс для зважування 3,2914 г іншого зразка, фактична вага становить від 3,2913 г до 3,2915 г, а абсолютна невизначеність все ще становить ± 0,1 мг.

Хоча абсолютні невизначеності в цих двох прикладах ідентичні, ми, ймовірно, вважаємо друге вимірювання більш точним, оскільки невизначеність є меншою часткою вимірюваного значення. Відносна невизначеність двох результатів була б

0,2 ÷ 74,1 = 0,0027 (приблизно 3 частини в 1000 (РРТ), або 0,3%)

0,0002 ÷ 3,2913 = 0,000084 (близько 0,8 РРТ, або 0,008%)

Відносні невизначеності широко використовуються для вираження надійності вимірювань, навіть тих, що для одного спостереження, і в цьому випадку невизначеність є невизначеністю вимірювального приладу. Відносні невизначеності можуть виражатися у вигляді частин на сто (відсотків), на тисячу (PPT), на мільйон, (PPM) і так далі.

Питання

1. Додавання та віднімання, обидва числа мають невизначеності

Найпростіший метод - просто додати абсолютну невизначеність.

Приклад: (6,3 ± 0,05 см) - (2,1 ± 0,05 см) = 4,2 ± 0,10 см
Однак це має тенденцію до завищення невизначеності, припускаючи найгірший можливий випадок, коли похибка в одній із величин знаходиться на максимальному позитивному значенні, тоді як інша величина - на максимумі мінімальне значення.

Статистична теорія повідомляє нам, що більш реалістичне значення невизначеності суми або різниці полягає в тому, щоб скласти квадрати кожної абсолютної невизначеності, а потім взяти квадратний корінь цієї суми. Застосовуючи це до вищевказаних значень, ми маємо

[(.05) ² + (.05) ²] ^½ = 0,07, тому результат становить 4,2 ± 0,07 см.

2. Множення або ділення, обидва числа мають невизначеності.

Перетворіть абсолютні невизначеності у відносні невизначеності та додайте їх. Або краще, складіть їх квадрати і візьміть квадратний корінь суми.

Приклад проблеми 3

Оцініть абсолютну похибку щільності, розраховану діленням (12,7 ± 0,05 г) на (10,0 ± 0,02 мл).

Рішення: Відносна невизначеність маси: 0,05/12,7 = 0,0039 = 0,39%
Відносна невизначеність об'єму: 0,02/10,0 = 0,002 = 0,2%
Відносна невизначеність щільності: [(.39) ² + (0,2) ²] ^½ = 0,44%
Маса ÷ об'єм: (12,7 г) ÷ (10,0 мл) = 1,27 г мл ^—1
Абсолютна невизначеність щільності: (± 0,044) х (1,27 г мл ^—1) = ± 0,06 г мл ^—1

3. Множення або ділення на чисте число

Тривіальний випадок; помножте або розділіть невизначеність на чисте число.