Skip to main content
LibreTexts - Ukrayinska

2.4: Значні цифри

  1. Last updated
  2. Save as PDF
  • Page ID
    22620

    • Anonymous
    • LibreTexts
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Мета навчання
    • Застосовуйте поняття значущих цифр, щоб обмежити вимірювання належною кількістю цифр.
    • Визнати кількість значущих цифр в заданій кількості.
    • Обмежте математичні результати належною кількістю значущих цифр.

    Якщо скористатися калькулятором для оцінки виразу 337/217, то вийде наступне:

    \[337\div 217=1.5529953917 \nonumber \nonumber \]

    і так далі для багатьох інших цифр. Хоча ця відповідь правильна, вона дещо самовпевнена. Ви починаєте з двох значень, кожен з яких має три цифри, а відповідь має дванадцять цифр? Це не має особливого сенсу з суворої числової точки зору.

    Розглянемо можливість використання лінійки для вимірювання ширини об'єкта, як показано на малюнку\(\PageIndex{1}\). Об'єкт, безумовно, більше 1 см завдовжки, тому ми знаємо, що перша цифра в нашому вимірі - 1. Ми бачимо, підраховуючи галочки на лінійці, що об'єкт стоїть як мінімум три галочки після 1. Якщо кожен кліщ становить 0,1 см, то ми знаємо, що предмет шириною не менше 1,3 см. Але наша лінійка не має більше галочок між 0.3 і 0.4 знаками, тому ми не можемо точно знати, скільки наступного знака після коми. Але практикуваним оком ми можемо це оцінити. Оцінимо його як приблизно шість десятих шляху між третьою і четвертою галочками, що оцінює наше соте місце як 6, тому ми виділимо вимір 1,36 см для ширини об'єкта.

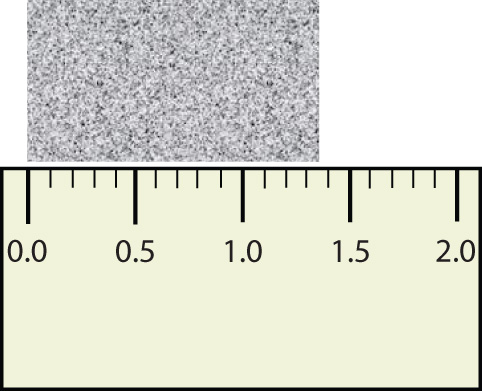
    Над безрозмірною лінійкою зображений сірий прямокутний об'єкт.
    Малюнок\(\PageIndex{1}\): Вираження ширини. Яким є правильний спосіб висловити ширину цього предмета?

    Чи є сенс намагатися повідомити тисячне місце для вимірювання? Ні, це не так; ми точно не впевнені в сотих місцях (зрештою, це була лише оцінка), тому оцінювати тисячне місце було б безрезультатно. Тоді наше найкраще вимірювання зупиняється на сотих місцях, і ми повідомляємо про 1,36 см як належне вимірювання.

    Це поняття звітності належної кількості цифр у вимірюванні або розрахунку називається значущими цифрами. Значні цифри (іноді їх називають значущими цифрами) представляють межі того, в яких значеннях вимірювання або розрахунку ми впевнені. Угода для вимірювання полягає в тому, що кількість, про яку повідомляється, повинна бути всіма відомими значеннями та першою оціночною величиною. Умовності для розрахунків обговорюються наступним чином.

    Приклад\(\PageIndex{1}\)

    Використовуйте кожну діаграму, щоб повідомити про вимірювання до належної кількості значущих цифр.

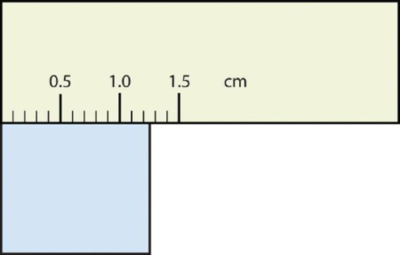
    Манометр в одиницях фунтів на квадратний дюйм.Вимірювальна лінійка з порожнім світло-блакитним блоком під ним.

    Рішення
    1. Стрілка знаходиться в межах від 4,0 до 5,0, тому вимірювання становить не менше 4,0. Стрілка знаходиться між третьою і четвертою невеликими галочками, так що це не менше 0,3. Доведеться оцінити останнє місце. Це виглядає приблизно на третину шляху через простір, тому оцінимо соті місця як 3. Поєднуючи цифри, ми маємо вимір 4,33 psi (psi означає «фунти на квадратний дюйм» і є одиницею тиску, як повітря в шині). Ми говоримо, що про вимірювання повідомляється три значущі цифри.
    2. Прямокутник шириною не менше 1,0 см, але, звичайно, не шириною 2,0 см, тому перша значна цифра - 1. Ширина прямокутника перевищує другу галочку, але не третю; якщо кожна галочка дорівнює 0,1, то прямокутник буде принаймні 0,2 в наступній значній цифрі. Ми повинні оцінити наступне місце, тому що немає маркувань, які б нас орієнтували. Здається, це приблизно на півдорозі між 0,2 і 0,3, тому ми оцінимо наступне місце, щоб бути 5. Таким чином, виміряна ширина прямокутника дорівнює 1,25 см. Знову ж таки, про вимірювання повідомляється три значущі цифри.
    Вправа\(\PageIndex{1}\)

    Якою буде ширина цього прямокутника?

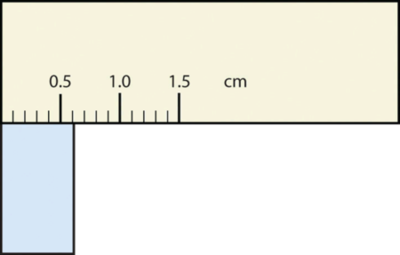
    Вимірювальна лінійка з порожнім світло-блакитним блоком під ним.

    Відповідь

    0,63 см

    У багатьох випадках вам дадуть вимір. Як ви можете зрозуміти, дивлячись які цифри є значущими? Наприклад, зареєстроване населення Сполучених Штатів становить 306 000 000. Чи означає це, що це рівно триста шість мільйонів, або відбувається якась оцінка?

    Наступні конвенції диктують, які числа в повідомленій вимірюванні є значними, а які не є значними:

    1. Будь-яка ненульова цифра є значущою.
    2. Будь-які нулі між ненульовими цифрами (тобто вбудованими нулями) є значними.
    3. Нулі в кінці числа без десяткової крапки (тобто кінцеві нулі) не є значними; вони служать лише для того, щоб поставити значущі цифри в правильні позиції. Однак нулі в кінці будь-якого числа з десятковою крапкою є значущими.
    4. Нулі на початку десяткового числа (тобто провідні нулі) не є значними; знову ж таки, вони служать лише для того, щоб поставити значущі цифри в правильні позиції.

    Так, за цими правилами чисельність населення США має лише три значущі цифри: 3, 6 і нуль між ними. Решта шість нулів просто ставлять 306 в мільйонну позицію. (Див. Малюнок\(\PageIndex{2}\) для іншого прикладу.)

    Початкові цифри pi показані: 3,14159.
    Малюнок\(\PageIndex{2}\): Значні цифри. Скільки цифр на цьому дисплеї насправді значні? (Громадське надбання.)
    Приклад\(\PageIndex{2}\)

    Дайте кількість значущих цифр в кожному вимірі.

    1. 36.7 м
    2. 0.006606 с
    3. 2,002 кг
    4. 306 490 000 осіб
    Рішення
    1. За правилом 1 всі ненульові цифри значущі, тому дане вимірювання має три значущі цифри.
    2. За правилом 4 перші три нулі не є значними, але за правилом 2 нуль між шістками дорівнює; отже, це число має чотири значущі цифри.
    3. За правилом 2 два нулі між двійками є значними, тому це вимірювання має чотири значущі цифри.
    4. Чотири кінцеві нулі в числі не є значними, але інші п'ять чисел є, тому це число має п'ять значущих цифр.
    Вправа\(\PageIndex{2}\)

    Дайте кількість значущих цифр в кожному вимірі.

    1. 0.000601 м
    2. 65.080 кг
    Відповідь на

    три значущі цифри

    Відповідь б

    п'ять значущих цифр

    Як обробляються значні цифри при розрахунках? Це залежить від того, який тип розрахунку виконується. Якщо обчислення є додаванням або відніманням, правило таке: обмежте повідомлену відповідь крайнім правим стовпцем, щоб всі числа мали спільні значні цифри. Наприклад, якщо ви повинні були додати 1,2 і 4,21, відзначимо, що перше число зупиняє свої значні цифри в десятому стовпці, тоді як друге число зупиняє свої значні цифри в стовпі сотих. Тому ми обмежуємо нашу відповідь десятим стовпцем.

    1.2 і 4.41 додаються, щоб отримати 5.61. Остаточна відповідь обмежується 5,6.

    Ми скидаємо останню цифру - 1 - тому що вона не є важливою для остаточної відповіді.

    Скидання позицій в сумах і різницях піднімає тему округлення. Хоча існує кілька умовностей, в цьому тексті ми візьмемо наступне правило: остаточну відповідь слід округлити в більшу сторону, якщо перша скинута цифра дорівнює 5 або більше, і округлити вниз, якщо перша скинута цифра менше 5.

    77.2 і 10.46 додаються, щоб отримати 87.66. Остаточний відповідь обмежений і округлений до 87,7.

    Приклад\(\PageIndex{3}\)

    Висловіть остаточну відповідь на належну кількість значущих цифр.

    1. 101.2 + 18,702 =?
    2. 202.88 − 1.013 =?
    Рішення
    1. Якщо ми скористаємося калькулятором для додавання цих двох чисел, ми отримаємо 119.902. Однак більшість калькуляторів не розуміють значущих цифр, і нам потрібно обмежитися остаточною відповіддю десятим місцем. Таким чином, скидаємо 02 і повідомляємо остаточну відповідь 119,9 (округлення вниз).
    2. Калькулятор відповість на 201.867. Однак ми повинні обмежити нашу остаточну відповідь сотими місцями. Оскільки перше число скидається - 7, що більше 5, ми округляємо і повідомляємо остаточну відповідь 201.87.
    Вправа\(\PageIndex{3}\)

    Висловіть відповідь за

    \[3.445 + 90.83 − 72.4 \nonumber \nonumber \]

    до належної кількості значущих цифр.

    Відповідь

    21.9

    Якщо виконувані операції - множення або ділення, правило таке: обмежте відповідь кількістю значущих цифр, які має значення даних з найменшою кількістю значущих цифр. Отже, якщо ми ділимо 23 на 448, які мають дві та три значущі цифри відповідно, ми повинні обмежитися остаточною повідомленою відповіддю двома значущими цифрами (меншою з двох і трьох значущих цифр):

    \[23\div 448= 0.051339286 \approx 0.051 \nonumber \nonumber \]

    Ті самі правила округлення застосовуються при множенні та діленні, як і при додаванні та відніманні.

    Приклад\(\PageIndex{4}\): Significant Figures

    Висловіть остаточну відповідь на належну кількість значущих цифр.

    1. 76,4 × 180,4 =?
    2. 934,9 ÷ 0,00455 =?
    Рішення
    1. Перше число має три значущі цифри, тоді як друге число має чотири значущі цифри. Тому нашу остаточну відповідь обмежуємо трьома значущими цифрами: 76,4 × 180,4 = 13 782,56 = 13 800.
    2. Перше число має чотири значущі цифри, тоді як друге число має три значущі цифри. Тому нашу остаточну відповідь обмежуємо трьома значущими цифрами: 934,9 ÷ 0,00455 = 205 472,5275... = 205 000.
    Вправа\(\PageIndex{4}\)

    Висловіть остаточну відповідь на належну кількість значущих цифр.

    1. 22,4 × 8,314 =?
    2. 1,381 ÷ 6,02 =?
    Відповідь на

    186

    Відповідь б

    0,229

    Як ви, напевно, вже зрозуміли, найбільшою проблемою у визначенні кількості значущих цифр у значенні є нуль. Нуль значний чи ні? Один із способів однозначно визначити, чи є нуль значущим чи ні - записати число в науковому позначенні. Наукові позначення будуть включати нулі в коефіцієнт числа тільки в тому випадку, якщо вони значні. Таким чином, число 8,666 × 10 6 має чотири значущі цифри. Однак число 8,6660 × 10 6 має п'ять значущих цифр. Цей останній нуль є значним; якби його не було, це не було б записано в коефіцієнті. Отже, коли сумніваєтеся в вираженні кількості значущих цифр в кількості, використовуйте наукові позначення і включайте кількість нулів, які дійсно значущі.

    Резюме

    • Значні цифри в кількості вказують на кількість відомих значень плюс одне місце, яке оцінюється.
    • Існують правила, для яких цифри в кількості є значними, а які не є значними.
    • У розрахунках, що передбачають додавання і віднімання, обмежте значні цифри, виходячи з самого правого місця, яке мають спільні всі значення.
    • При розрахунках, що передбачають множення і ділення, обмежуйте значні цифри найменшою кількістю значущих цифр у всіх значеннях даних.