1.10: Вирішення проблем - перетворення одиниць та оцінка відповідей
- Page ID
- 21739
- Перетворіть значення, повідомлене в одній одиниці, до відповідного значення в іншій одиниці.
Уміння конвертувати з однієї одиниці в іншу - важливий навик. Наприклад, медсестра з таблетками аспірину 50 мг, яка повинна вводити пацієнту 0,2 г аспірину, повинна знати, що 0,2 г дорівнює 200 мг, тому необхідні 4 таблетки. На щастя, існує простий спосіб перетворення з однієї одиниці в іншу.
Коефіцієнти перетворення
Якщо ви дізналися описані раніше одиниці СІ і приставки, то знаєте, що 1 см - це 1/100 метра.
\[ 1\; \rm{cm} = \dfrac{1}{100} \; \rm{m} \nonumber \]
або
\[100\; \rm{cm} = 1\; \rm{m} \nonumber \]
Припустимо, розділимо обидві сторони рівняння на 1 м (і на число, і одиницю):
\[\mathrm{\dfrac{100\:cm}{1\:m}=\dfrac{1\:m}{1\:m}} \nonumber \]
Поки ми виконуємо одну і ту ж операцію з обох сторін знака рівності, вираз залишається рівністю. Подивіться на праву частину рівняння; тепер воно має таку ж величину в чисельнику (верхній), як у знаменнику (внизу). Будь-який дріб, який має однакову величину в чисельнику і знаменнику, має значення 1:
Ми знаємо, що 100 см - це 1 м, тому у нас однакова кількість на верхній і нижній частині нашої фракції, хоча вона виражена в різних одиницях. Дріб, який має еквівалентні величини в чисельнику і знаменнику, але виражений в різних одиницях, називається коефіцієнтом перетворення.
Ось простий приклад. Скільки сантиметрів в 3,55 м? Можливо, ви зможете визначити відповідь у себе в голові. Якщо в кожному метрі 100 см, то 3,55 м дорівнює 355 см. Щоб вирішити задачу більш формально з коефіцієнтом перетворення, спочатку запишемо задану нам величину, 3,55 м Потім множимо цю величину на коефіцієнт перетворення, який такий же, як і множення її на 1. Ми можемо записати 1 як\(\mathrm{\frac{100\:cm}{1\:m}}\) і помножити:
\[ 3.55 \; \rm{m} \times \dfrac{100 \; \rm{cm}}{1\; \rm{m}} \nonumber \]
3.55 м можна розглядати як дріб з 1 в знаменнику. Оскільки m, абревіатура для метрів, зустрічається і в чисельнику, і в знаменнику нашого виразу, вони скасовують:
\[\dfrac{3.55 \; \cancel{\rm{m}}}{ 1} \times \dfrac{100 \; \rm{cm}}{1 \; \cancel{\rm{m}}} \nonumber \]
Останнім кроком є виконання розрахунку, який залишається після скасування одиниць:
\[ \dfrac{3.55}{1} \times \dfrac{100 \; \rm{cm}}{1} = 355 \; \rm{cm} \label{Ex1} \]
У остаточній відповіді опускаємо 1 в знаменнику. Таким чином, за більш формальною процедурою ми знаходимо, що 3,55 м дорівнює 355 см. Узагальнене опис цього процесу виглядає наступним чином:
\[\text{quantity (in old units)} \times \text{conversion factor} = \text{quantity (in new units)} \nonumber \]
Можливо, вам буде цікаво, чому ми використовуємо, здавалося б, складну процедуру для простого перетворення. У більш пізніх дослідженнях проблеми з перетворенням, з якими ви зіткнетеся, не завжди будуть такими простими. Якщо ви зможете освоїти техніку застосування коефіцієнтів перерахунку, вам вдасться вирішити велику кількість різноманітних завдань.
У попередньому прикладі (Equation\ ref {Ex1}) ми використовували дріб\(\frac{100 \; \rm{cm}}{1 \; \rm{m}}\) як коефіцієнт перетворення. Чи коефіцієнт перетворення\(\frac{1 \; \rm m}{100 \; \rm{cm}}\) також дорівнює 1? Так, він має таку ж величину в чисельнику, як і в знаменнику (за винятком того, що вони виражені в різних одиницях). Чому ми не використали цей коефіцієнт перетворення? Якби ми використовували другий коефіцієнт перетворення, вихідну одиницю не скасували б, а результат був би безглуздим. Ось що ми б отримали:
\[ 3.55 \; \rm{m} \times \dfrac{1\; \rm{m}}{100 \; \rm{cm}} = 0.0355 \dfrac{\rm{m}^2}{\rm{cm}} \nonumber \]
Щоб відповідь була значущою, ми повинні побудувати коефіцієнт перетворення у формі, яка змушує вихідну одиницю скасувати. \(\PageIndex{1}\)На малюнку показана концептуальна карта для побудови належного перетворення.
Значні цифри в конверсіях
Як коефіцієнти перерахунку впливають на визначення значущих цифр? Числа в коефіцієнтах перетворення на основі змін префіксів, таких як кілограми в грами, не враховуються при визначенні значущих цифр при розрахунку, оскільки числа в таких коефіцієнтах перетворення є точними. Точні числа - це визначені або підраховані числа, а не вимірювані числа, і можуть розглядатися як мають нескінченну кількість значущих цифр. (Іншими словами, 1 кг дорівнює рівно 1000 г, за визначенням кіло-.) Підраховані числа також точні. Якщо в класі 16 учнів, число 16 є точним. На відміну від цього, коефіцієнти перетворення, які походять від вимірювань (наприклад, щільність, як ми побачимо незабаром) або є наближеннями, мають обмежену кількість значущих цифр і повинні враховуватися при визначенні значущих цифр остаточної відповіді.
- Середній обсяг крові у дорослого чоловіка становить 4,7 л. Що це за обсяг в мілілітрах?
- Колібрі може махати крилами один раз в 18 мс. Скільки секунд в 18 мс?
Рішення
- Почнемо з того, що нам дають, 4,7 л. Хочемо поміняти агрегат з літрів на мілілітри. Є 1000 мл в 1 л. З цієї залежності можна побудувати два коефіцієнти перетворення:
\[ \dfrac{1\; \rm{L}}{1,000\; \rm{mL}} \; \text{ or } \; \dfrac{1,000 \; \rm{mL}}{1\; \rm{L}} \nonumber \]
Ми використовуємо коефіцієнт перетворення, який скасує вихідну одиницю, літри, і введемо одиницю, в яку ми конвертуємо, яка є мілілітрами. Коефіцієнт перетворення, який робить це, той, що знаходиться праворуч.
\[ 4.7 \cancel{\rm{L}} \times \dfrac{1,000 \; \rm{mL}}{1\; \cancel{\rm{L}}} = 4,700\; \rm{mL} \nonumber \]
Оскільки числа в коефіцієнті перетворення точні, ми не враховуємо їх при визначенні кількості значущих цифр у підсумковій відповіді. Таким чином, ми повідомляємо дві значущі цифри в остаточній відповіді.
- Ми можемо побудувати два коефіцієнти перетворення з взаємозв'язків між мілісекундами та секундами:
\[ \dfrac{1,000 \; \rm{ms}}{1\; \rm{s}} \; \text{ or } \; \dfrac{1\; \rm{s}}{1,000 \; \rm{ms}} \nonumber \]
Щоб перетворити 18 мс в секунди, ми вибираємо коефіцієнт перетворення, який скасує мілісекунди і введе секунди. Коефіцієнт перерахунку праворуч є відповідним. Налаштовуємо конверсію наступним чином:
\[ 18 \; \cancel{\rm{ms}} \times \dfrac{1\; \rm{s}}{1,000 \; \cancel{\rm{ms}}} = 0.018\; \rm{s} \nonumber \]
Числові значення коефіцієнта перетворення не впливають на наше визначення кількості значущих цифр у підсумковій відповіді.
Виконайте кожне перетворення.
- 101,000 нс в секунди
- 32.08 кг в грами
- Відповідь
-
\[ 101,000 \cancel{\rm{ns}} \times \dfrac{1\; \rm{s}}{1,000,000,000\; \cancel{\rm{ns}}} = 0.000101\; \rm{s} \nonumber \]
- Відповідь б
-
\[ 32.08 \cancel{\rm{kg}} \times \dfrac{1,000 \; \rm{g}}{1\; \cancel{\rm{kg}}} = 32,080\; \rm{g} \nonumber \]
Коефіцієнти перерахунку з різних одиниць
Коефіцієнти перетворення також можуть бути побудовані для перетворення між різними видами одиниць. Наприклад, щільність може використовуватися для перетворення між масою і об'ємом речовини. Розглянемо ртуть, яка є рідиною кімнатної температури і має щільність 13,6 г/мл. Щільність говорить нам, що 13,6 г ртуті мають обсяг 1 мл. Ми можемо написати ці відносини наступним чином:
13,6 г ртуті = 1 мл ртуті
Цей зв'язок може бути використаний для побудови двох коефіцієнтів перетворення:
\[\mathrm{\dfrac{13.6\:g}{1\:mL}\:and\:\dfrac{1\:mL}{13.6\:g}} \nonumber \]
Який з них ми використовуємо? Це залежить, як завжди, від одиниць, які нам потрібно скасувати і ввести. Наприклад, припустимо, ми хочемо дізнатися масу 16 мл ртуті. Ми б використовували коефіцієнт перетворення, який має мілілітри внизу (так що мілілітровий блок скасовується) та грами зверху, щоб наша остаточна відповідь мала одиницю маси:
\[ \begin{align*} \mathrm{16\:\cancel{mL}\times\dfrac{13.6\:g}{1\:\cancel{mL}}} &= \mathrm{217.6\:g} \\[4pt] &\approx \mathrm{220\:g} \end{align*} \nonumber \]
На останньому кроці ми обмежуємо нашу остаточну відповідь двома значущими цифрами, оскільки об'ємна кількість має лише дві значущі цифри; 1 в одиниці об'єму вважається точним числом, тому воно не впливає на кількість значущих цифр. Інший коефіцієнт перетворення був би корисним, якби нам дали масу і попросили знайти обсяг, як ілюструє наступний приклад.
Щільність може використовуватися як коефіцієнт перетворення між масою і об'ємом.
Ртутний термометр для вимірювання температури пацієнта містить 0,750 г ртуті. Який обсяг цієї маси ртуті?
Рішення
Оскільки ми починаємо з грам, ми хочемо використовувати коефіцієнт перетворення, який має грами в знаменнику. Грамова одиниця скасує алгебраїчно, а мілілітри будуть введені в чисельник.
\[ \begin{align*} 0.750 \; \cancel{\rm{g}} \times \dfrac{1\; \rm{mL}}{13.6 \; \cancel{\rm{g}}} &= 0.055147 \ldots \; \rm{mL} \\[4pt] &\approx 0.0551\; \rm{mL} \end{align*} \nonumber \]
Остаточну відповідь ми обмежили трьома значущими цифрами.
Який обсяг 100,0 г повітря, якщо його щільність становить 1,3 г/л?
- Відповідь
-
\[100.0 \cancel{\rm{g}} \times \dfrac{1\; \rm{L}}{1.3\; \cancel{\rm{g}}} = 76.92307692\; \rm{L} ≈ 77 L \nonumber \]
Оскільки щільність (1,3 г/л) має всього 2 значущих цифри, ми округляємо остаточну відповідь до 2 значущих цифр.
Вирішення проблем з декількома конверсіями
Іноді вам доведеться виконати більше одного перетворення, щоб отримати потрібну одиницю. Наприклад, припустимо, ви хочете перетворити 54,7 км в міліметри. Ви можете або запам'ятати співвідношення між кілометрами і міліметрами, або зробити перетворення в два кроки. Більшість людей вважають за краще конвертувати по кроках.
Щоб зробити поетапне перетворення, ми спочатку конвертуємо задану суму в базову одиницю. В даному прикладі базовою одиницею є метри. Ми знаємо, що в 1 км знаходиться 1000 м:
\[ 54.7\; \cancel{\rm{km}} \times \dfrac{1,000 \; \rm{m}}{1\; \cancel{\rm{km}}} = 54,700\; \rm{m} \nonumber \]
Потім беремо результат (54 700 м) і перетворюємо його в міліметри, пам'ятаючи, що є\(1,000\; \rm{mm}\) на кожен\(1\; \rm{m}\):
\[ \begin{align*} 54,700 \; \cancel{\rm{m}} \times \dfrac{1,000 \; \rm{mm}}{1\; \cancel{\rm{m}}} &= 54,700,000 \; \rm{mm} \\[4pt] &= 5.47 \times 10^7\; \rm{mm} \end{align*} \nonumber \]
Остаточну відповідь ми висловили в науковому позначенні.
Як ярлик, обидва етапи перетворення можуть бути об'єднані в єдиний багатоступінчастий вираз:
Концепція Карта
Розрахунок
\[ \begin{align*} 54.7\; \cancel{\rm{km}} \times \dfrac{1,000 \; \cancel{\rm{m}}}{1\; \cancel{\rm{km}}} \times \dfrac{1,000 \; \rm{mm}}{1\; \cancel{\rm{m}}} &= 54,700,000 \; \rm{mm} \\[4pt] &= 5.47 \times 10^7\; \rm{mm} \end{align*} \nonumber \]
На кожному кроці попередній блок скасовується і проводиться наступний блок у послідовності, кожен наступний блок скасовується, поки не залишиться лише одиниця, необхідна у відповіді.
Будь-який метод - один крок за раз, або всі кроки разом - прийнятний. Якщо виконати всі кроки разом, обмеження на належну кількість значущих цифр слід робити після останнього кроку. Поки математика виконується правильно, ви повинні отримати ту ж відповідь незалежно від того, який метод ви використовуєте.
Перетворіть 58.2 мс в мегасекунди за один багатоступінчастий розрахунок.
Рішення
Спочатку перетворіть задану одиницю (мс) на базову одиницю - у цьому випадку секунди, а потім перетворіть секунди в кінцеву одиницю, мегасекунди:
Концепція Карта
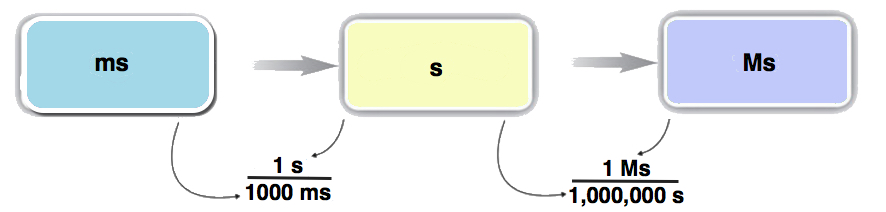
Розрахунок
\[ \begin{align*} 58.2 \; \cancel{\rm{ms}} \times \dfrac{\cancel{1 \rm{s}}}{1,000\; \cancel{\rm{ms}}} \times \dfrac{1\; \rm{Ms}}{1,000,000\; \cancel{ \rm{s}}} &=0.0000000582\; \rm{Ms} \\[4pt] &= 5.82 \times 10^{-8}\; \rm{Ms} \end{align*} \nonumber \]
Жоден коефіцієнт перерахунку не впливає на кількість значущих цифр у підсумковій відповіді.
Перетворіть 43.007 мг на кілограми за один багатоступінчастий розрахунок.
- Відповідь
-
\[ \begin{align*} 43.007 \; \cancel{\rm{mg}} \times \dfrac{\cancel{1 \rm{g}}}{1,000\; \cancel{\rm{mg}}} \times \dfrac{1\; \rm{kg}}{1,000\; \cancel{ \rm{g}}} &=0.000043007\; \rm{kg} \\[4pt] &= 4.3007 \times 10^{-5}\; \rm{kg} \end{align*} \nonumber \].
Жоден коефіцієнт перерахунку не впливає на кількість значущих цифр у підсумковій відповіді.
Фармацевт відпускає препарати, які були призначені лікарем. Хоча це може здатися простим, фармацевти в Сполучених Штатах повинні мати докторську ступінь у фармації та мати ліцензію держави, в якій вони працюють. Більшість аптечних програм вимагають чотирирічного навчання в спеціальності аптечної школи.
Фармацевти повинні знати багато хімії та біології, щоб вони могли зрозуміти вплив ліків (які є хімічними речовинами, врешті-решт) на організм. Фармацевти можуть консультувати лікарів щодо вибору, дозування, взаємодії та побічних ефектів ліків. Вони також можуть консультувати пацієнтів щодо правильного використання своїх ліків, включаючи те, коли і як правильно приймати конкретні препарати. Фармацевтів можна знайти в аптеках, лікарнях та інших медичних установах.
Цікаво, що застаріла назва фармацевта - хімік, який використовувався, коли фармацевти раніше робили багато препаратів або компаундирования. В сучасний час фармацевти рідко з'єднують власні препарати, але знання наук, в тому числі і хімії, допомагають їм надавати цінні послуги в підтримці здоров'я кожного.
Ключ на винос
- Одиниця може бути перетворена в іншу одиницю того ж типу з коефіцієнтом перетворення.
Концепція Огляд Вправи
- Як визначити, яка величина в коефіцієнті перерахунку йде в знаменник дробу?
- Викладіть рекомендації щодо визначення значущих цифр при використанні коефіцієнта переведення.
- Напишіть концептуальну карту (план) того, як ви конвертуєте\(1.0 \times 10^{12}\) нано літри (nL) в кілолітри (kL).
Відповіді
- Одиниця, яку ви хочете скасувати з чисельника, йде в знаменник коефіцієнта перерахунку.
- Точні числа, що з'являються в багатьох коефіцієнтах перетворення, не впливають на кількість значущих цифр, інакше застосовуються звичайні правила множення і ділення для значущих цифр.
- Концептуальна карта: Перетворіть дані (нанолітри, nL) в літри; потім перетворіть літри в кілолітри.
