Skip to main content
LibreTexts - Ukrayinska

3.16: Значні цифри

  1. Last updated
  2. Save as PDF
  • Page ID
    19577

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Обмеження швидкості мають вбудовану невизначеність
    Малюнок\(\PageIndex{1}\) (Кредит: Користувач: Whispertome/Wikimedia Commons; Джерело: http://commons.wikimedia.org/wiki/File:JacintoCitySignJacintoCityTexas.JPG(opens у новому вікні); Ліцензія: Громадське надбання)

    Як швидко ви їдете?

    Коли ви входите в місто Хасінто Сіті, штат Техас, знак говорить вам, що обмеження швидкості становить 30 миль на годину. Але що робити, якщо вам трапиться їхати 31 милю на годину? У вас біда? Ймовірно, ні, тому що існує певна кількість вільного шляху, вбудованого в забезпечення виконання регулювання. Більшість спідометрів не дуже точно вимірюють швидкість транспортного засобу і можуть бути легко вимкнені на милю або близько того (з іншого боку, радіолокаційні вимірювання набагато точніші). Отже, пара миль на годину різниця не матиме такого значення. Однак, якщо ви розтягнете ліміти далі, ви можете в кінцевому підсумку отримати квиток на дорожній рух.

    Значні цифри

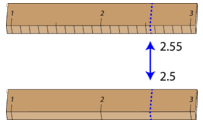
    Значні цифри у вимірюванні складаються з усіх певних цифр у цьому вимірі, плюс одна невизначена або передбачувана цифра. На ілюстрації лінійки нижче нижня лінійка дала довжину з 2 значущими фігурами, тоді як верхня лінійка давала довжину з 3 значущими фігурами. У правильно повідомленому вимірюванні кінцева цифра є значною, але не певною. Незначні цифри не повідомляються. З будь-якою лінійкою неможливо було б повідомити довжину\(2.553 \: \text{cm}\), оскільки немає можливості оцінити тисячну цифру. 3 не є значним і не буде повідомлено.

    Малюнок\(\PageIndex{2}\): Вимірювання двома різними лінійками. (Кредит: Крістофер Auyeung; Джерело: CK-12 Foundation; Ліцензія: CC BY-NC-SA 3.0 (відкривається в новому вікні))

    Коли ви дивитеся на повідомлене вимірювання, необхідно вміти підраховувати кількість значущих цифр. У таблиці нижче детально описані правила визначення кількості значущих цифр в повідомленому вимірі. Для прикладів в таблиці припустимо, що величини - це правильно повідомлені значення вимірюваної величини.

    Правило Приклади
    Малюнок\(\PageIndex{1}\): Правила значущих фігур
    1. Усі ненульові цифри у вимірюванні є значними.
    • 237 має три значущі цифри.
    • 1.897 має чотири значущі цифри.
    2. Нулі, що з'являються між іншими ненульовими цифрами, завжди значні.
    • 39 004 має п'ять значущих цифр.
    • 5.02 має три значущі цифри.
    3. Нулі, які з'являються перед усіма ненульовими цифрами, називаються лівими нулями. Нулі лівого кінця ніколи не є значними.
    • 0,008 має одну істотну цифру.
    • 0.000416 має три значущі цифри.
    4. Нулі, які з'являються після всіх ненульових цифр, називаються нулями правого кінця. Нулі правого краю в числі, якому не вистачає десяткової крапки, не є значними.
    • 140 має дві значущі цифри.
    • 75,210 має чотири значущі цифри.
    5. Нулі правого краю в числі з десятковою крапкою є значущими. Це вірно, чи виникають нулі до або після коми.
    • 620.0 має чотири значущі цифри.
    • 19.000 має п'ять значущих цифр.

    Потрібно підкреслити, що говорити певну цифру не є значною, не означає, що вона не важлива або може бути залишена осторонь. Хоча нуль при вимірюванні 140 може не бути значним, значення не може бути просто повідомлено як 14. Незначний нуль функціонує як заповнювач для десяткової крапки. Коли числа записуються в науковому позначенні, це стає більш очевидним. Вимірювання 140 можна записати як\(1.4 \times 10^2\) з двома значними цифрами в коефіцієнті. Для числа з лівими нулями, наприклад 0.000416, його можна записати як\(4.16 \times 10^{-4}\) з 3 значущими цифрами. У деяких випадках наукові позначення є єдиним способом правильно вказати правильну кількість значущих цифр. Для того, щоб повідомити про значення 15,000,000 з чотирма значними цифрами, його потрібно було б написати як\(1.500 \times 10^7\). Праві нулі після 5 є значними. Початкове число 15 000 000 має лише дві значні цифри.

    Інтерактивний елемент

    Потренуйтеся використовувати значні цифри в цьому моделюванні.

    Резюме

    • Значні цифри дають вказівку на достовірність вимірювання.
    • Правила дозволяють приймати рішення про те, скільки цифр використовувати в будь-якій ситуації.

    Рецензія

    1. Про що нам говорить значна цифра?
    2. Що таке лівий нуль?
    3. Що таке правий нуль?
    4. Що робить незначний нуль?