Skip to main content
LibreTexts - Ukrayinska

3.14: Вимірювання невизначеності

  1. Last updated
  2. Save as PDF
  • Page ID
    19569

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Поліцейська лінія Не перетинає стрічку на розмитому тлі.
    Малюнок\(\PageIndex{1}\) (Кредит: Тоні Вебстер; Джерело: Вікісховище Вікімедіа, Поліцейська лінія злочину (відкривається у новому вікні) [commons.wikimedia.org]; Ліцензія: CC BY-SA 4.0 (відкривається у новому вікні))

    Як співробітники міліції ідентифікують злочинців?

    Після того, як було здійснено пограбування банку, поліція попросить свідків описати злодіїв. Зазвичай вони отримають таку відповідь, як «середня висота». Інші можуть сказати щось уздовж лінії «між 5 футів 8 дюймів і 5 футів 10 дюймів». В обох випадках існує значна кількість невизначеності щодо зростання злочинців.

    Невизначеність вимірювання

    Якась похибка або невизначеність завжди існує в будь-якому вимірі. Величина невизначеності залежить як від майстерності вимірювача, так і від якості вимірювального інструменту. У той час як деякі баланси здатні вимірювати маси тільки до найближчого\(0.1 \: \text{g}\), інші високочутливі баланси здатні вимірювати до найближчого\(0.001 \: \text{g}\) або навіть краще. Багато вимірювальні інструменти, такі як лінійки та градуйовані циліндри, мають невеликі лінії, які потрібно уважно прочитати, щоб зробити вимірювання. На малюнку нижче показані дві лінійки, які роблять однаковий вимір об'єкта (позначені синьою стрілкою).

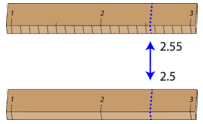
    Малюнок\(\PageIndex{2}\): Невизначеність у вимірюванні. (Кредит: Крістофер Auyeung; Джерело: CK-12 Foundation; Ліцензія: CC BY-NC-SA 3.0 (відкривається в новому вікні))

    За допомогою будь-якої лінійки зрозуміло, що довжина предмета знаходиться між\(2\) і\(3 \: \text{cm}\). Нижня лінійка не містить міліметрових розміток. За допомогою цієї лінійки можна оцінити десяту цифру, а довжину можна повідомити як\(2.5 \: \text{cm}\). Однак інша людина може судити про те, що вимірювання є\(2.4 \: \text{cm}\) чи можливо\(2.6 \: \text{cm}\). У той час як 2 відомо напевно, значення десятих цифр є невизначеним.

    Верхня лінійка містить позначки на десяті частки сантиметра (міліметри). За допомогою цієї лінійки можна виміряти той же об'єкт, що і\(2.55 \: \text{cm}\). Вимірювач здатний оцінити цифру сотих, оскільки він може бути впевнений, що цифра десятих - це 5. Знову ж таки, інший вимірювач може повідомити довжину бути\(2.54 \: \text{cm}\) або\(2.56 \: \text{cm}\). У цьому випадку є дві певні цифри (2 і 5), причому цифра сотих є невизначеною. Зрозуміло, що верхня лінійка - це чудова лінійка для вимірювання довжини якомога точніше.

    Резюме

    • Невизначеність існує у всіх вимірах.
    • На ступінь невизначеності частково впливає якість вимірювального інструменту.

    Рецензія

    1. Що таке невизначеність у вимірах?
    2. Чому верхня лінійка більш надійна в вимірюванні довжини, ніж нижня лінійка?
    3. Як можна зробити точнішою верхню лінійку?