11.2: Кластерний аналіз

Last updated

Oct 25, 2022
Save as PDF
- 11.1: Що ми маємо на увазі під структурою?
- 11.3: Аналіз основних компонентів

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

У попередньому розділі ми розглянули спектри 24 зразків на 635 довжині хвиль, відображаючи дані шляхом побудови поглинання як функції довжини хвилі. Інший спосіб вивчити дані полягає в тому, щоб побудувати поглинання кожного зразка на одній довжині хвилі проти поглинання того ж зразка на другій довжині хвилі, як ми бачимо на наступному малюнку з використанням довжин хвиль 403,3 нм і 508,7 нм. Зверніть увагу, що ця ділянка передбачає базову структуру для наших даних, оскільки точки 24 займають простір трикутної форми. визначається зразками, ідентифікованими як 1, 2 та 3.

Малюнок $\PageIndex{1}$ : Графік, що показує значення поглинання для зразків 24 з малюнка 11.1.1 на довжині хвиль 400.3 нм і 508,7 нм. Цифри поруч з точками є значеннями індексу для зразків.

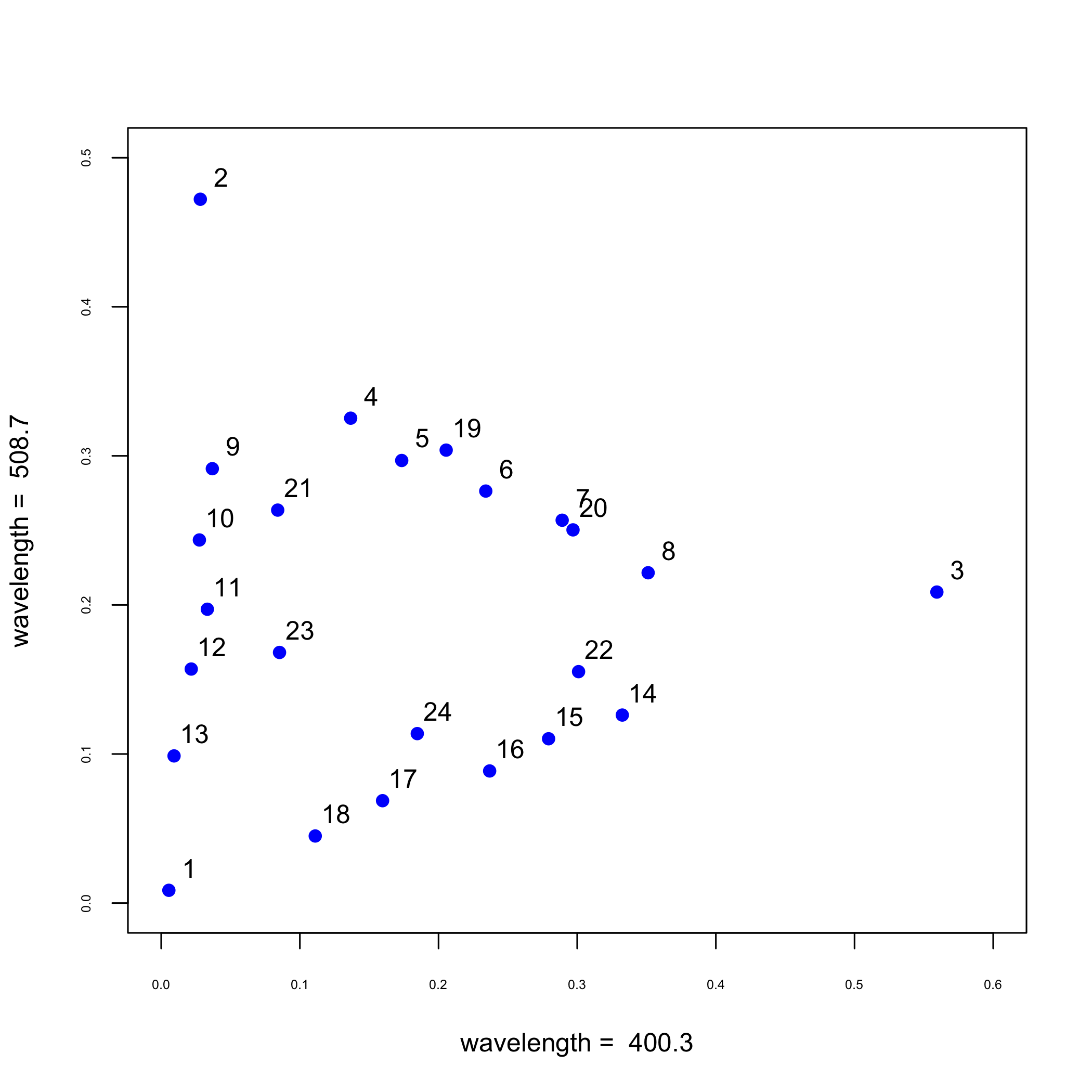
Ми можемо розширити цей аналіз на три довжини хвиль, як ми бачимо на наступному малюнку, і до цілих 635 довжин хвиль (Звичайно, ми не можемо вивчити сюжет цього, як він існує в 635 вимірному просторі!).

Рисунок $\PageIndex{2}$ : Графік, що показує значення поглинання для зразків 24 з малюнка 11.1.1 на довжині хвиль 400.3 нм, 508,7 нм та 801,8 нм. Колір точок показує поглинання на 801,8 нм, що є віссю z. Цифри поруч з точками є значеннями індексу для зразків. Зверніть увагу, що 24 точки тут також проживають у просторі трикутної форми.

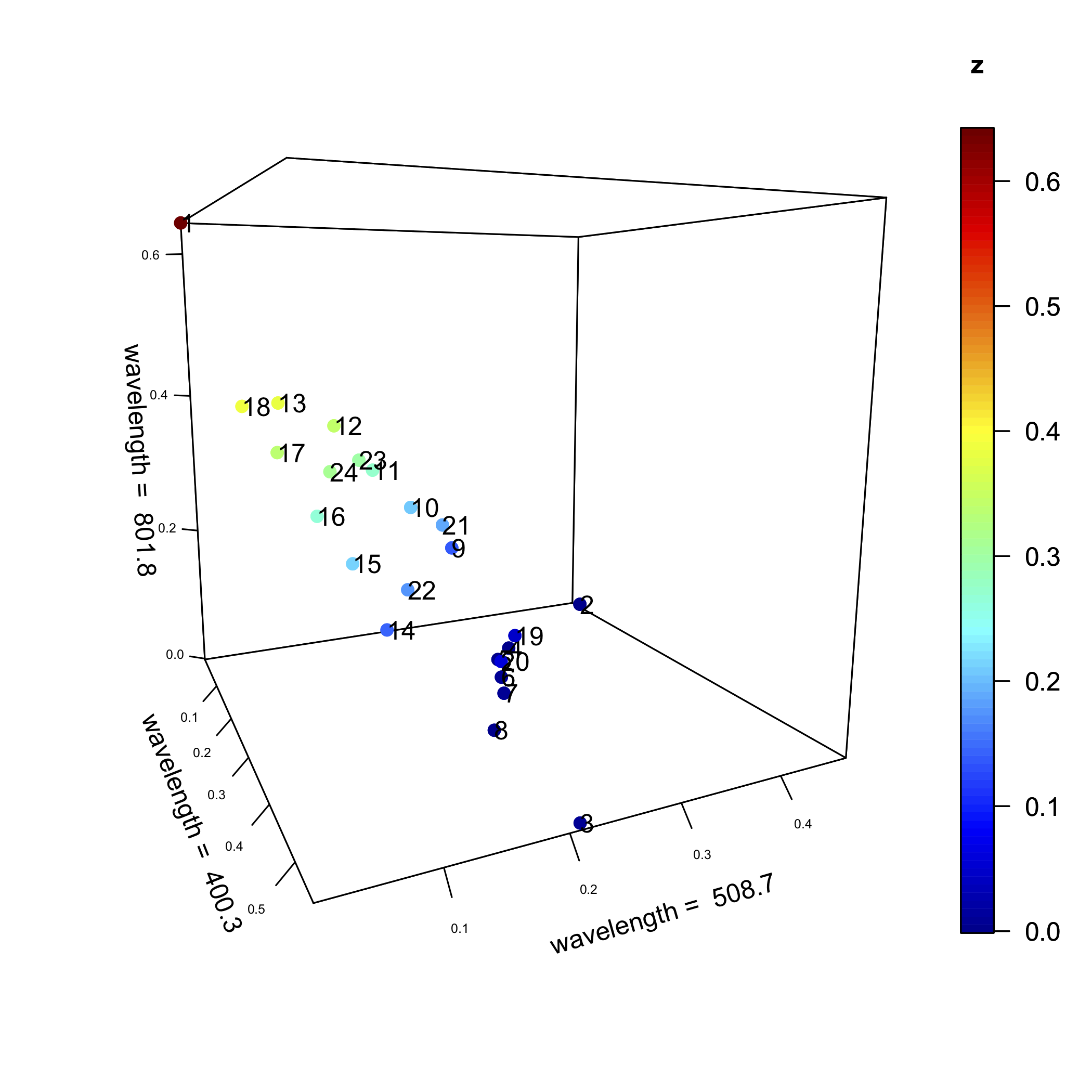
Як на малюнку, так $\PageIndex{1}$ і на малюнку $\PageIndex{2}$ (і на графіках вищих розмірів, які ми не можемо відобразити) деякі зразки ближче один до одного в просторі, ніж інші точки. Наприклад, на малюнку зразки 7 і 20 розташовані ближче один до одного $\PageIndex{1}$ , ніж будь-яка інша пара зразків; зразки 2 і 3, однак, знаходяться далі один від одного, ніж будь-яка інша пара зразків.

Як працює кластерний аналіз?

Кластерний аналіз - це спосіб вивчити наші дані з точки зору схожості зразків один з одним. Малюнок $\PageIndex{3}$ окреслює кроки, використовуючи невеликий набір з шести точок, визначених двома змінними, a та b. Панель (а) показує шість точок даних. Дві точки, найближчі за відстанню, - це 3 та 4, які складають перше скупчення і які ми замінюємо червоною точкою посередині між ними, як показано на панелі (b). Наступні дві точки, найближчі за відстанню, - це 2 та 6, які складають друге скупчення і які ми замінюємо червоною точкою між ними, як показано на панелі (c). Продовжуючи таким чином, дає результати в панелі (d), де третій кластер об'єднує точки 2, 3, 4 та 6, четвертий кластер об'єднує точки 1, 2, 3, 4 та 6, а остаточний кластер об'єднує всі шість пунктів.

Малюнок $\PageIndex{3}$ : Приклад роботи кластерного аналізу. Докладніше про це дивіться в тексті.

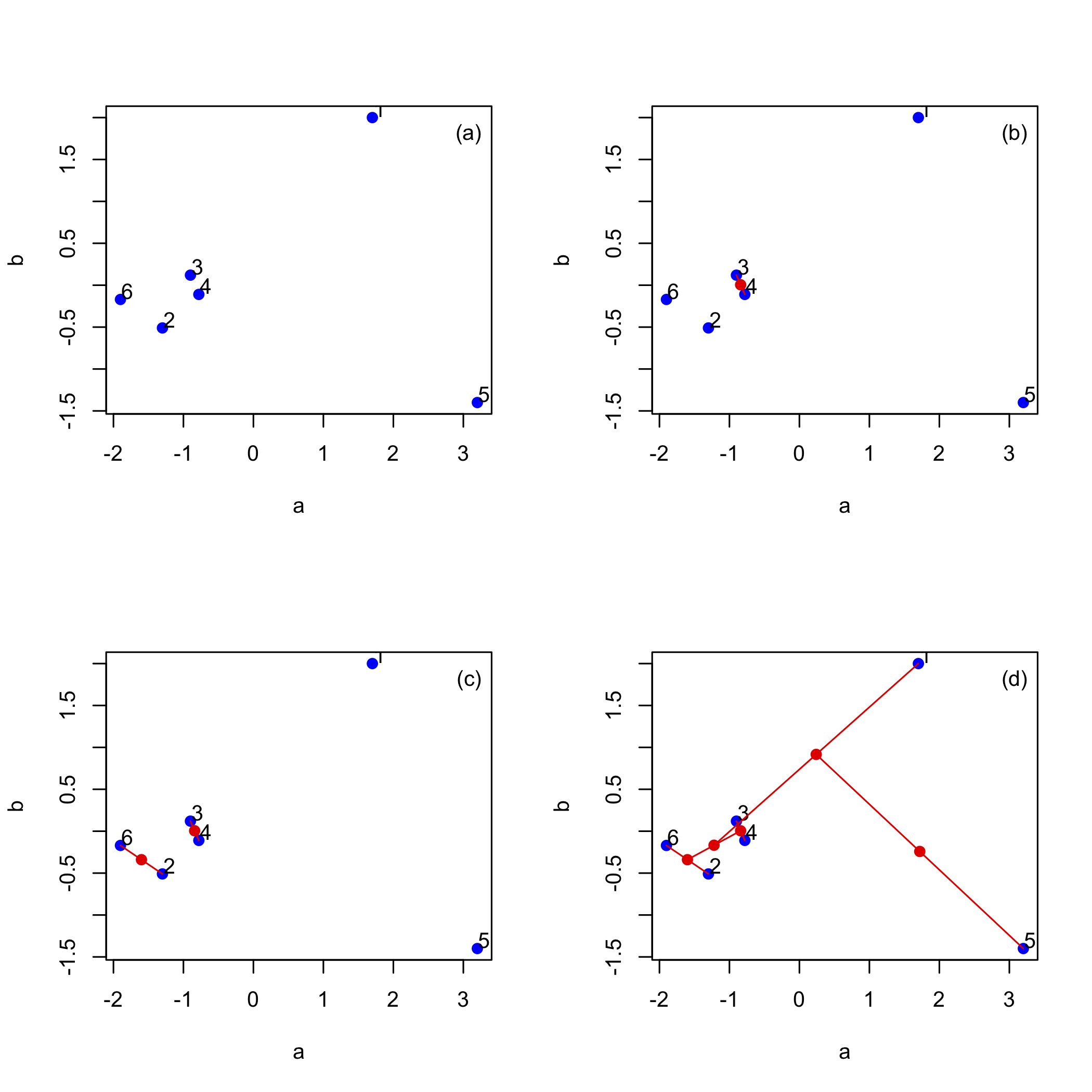
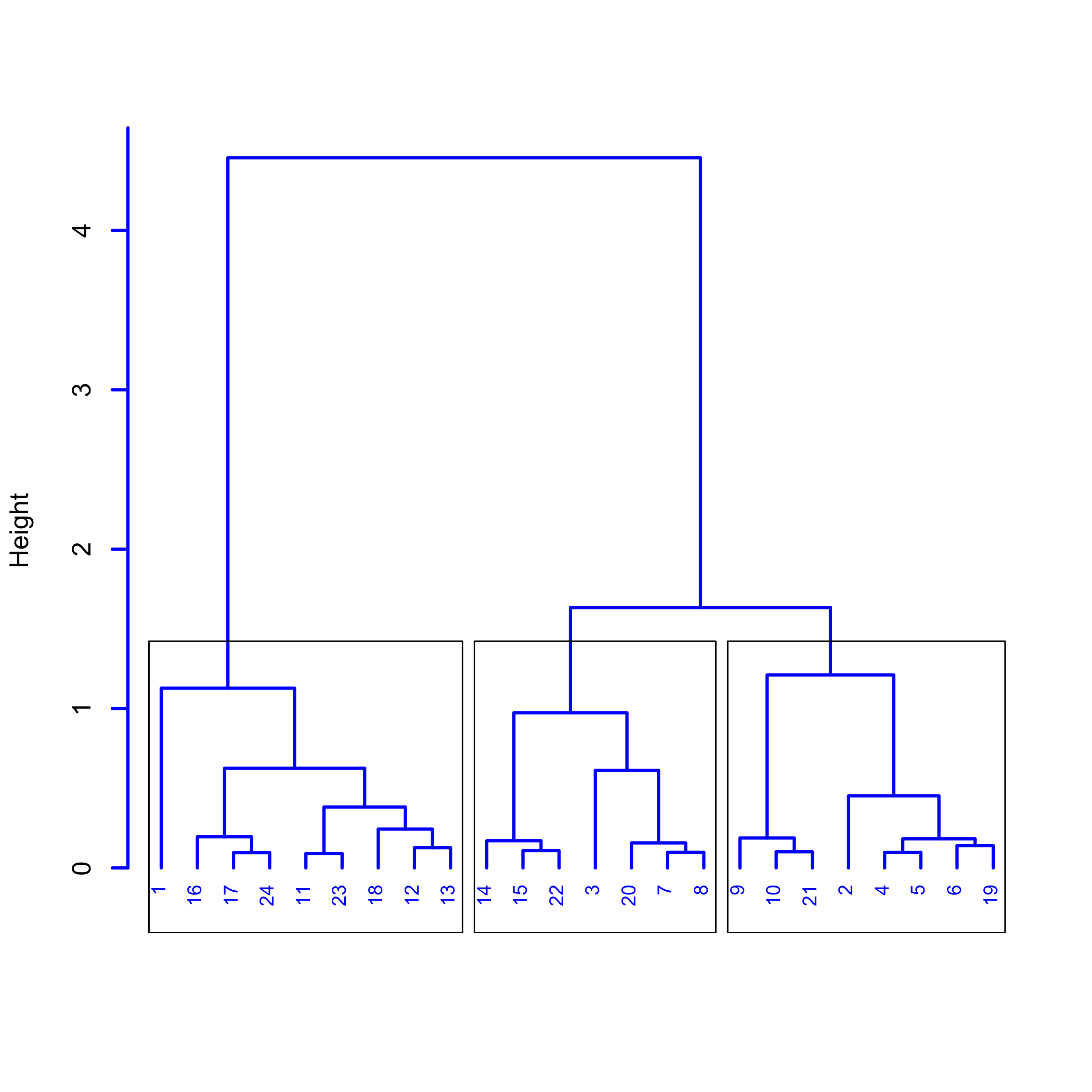
Для візуалізації кластерів, з точки зору ідентифікації точок в кластерах, порядку, в якому утворюються кластери, і відносної подібності різниці між точками і кластерами виводимо інформацію на малюнку у $\PageIndex{3d}$ вигляді дендрограми, показаної на малюнку $\PageIndex{4}$ , яка показує, наприклад, що скупчення точок 3 і 4, а з 2 і 6 більше схожі один на одного, ніж вони є точкою 1 і точкою 6. Вертикальна шкала, яка ідентифікується як Висота, забезпечує міру відстані окремих точок або скупчень точок один від одного.

Малюнок $\PageIndex{4}$ : Результати кластерного аналізу на малюнку $\PageIndex{3d}$ відображаються у вигляді дендрограми.

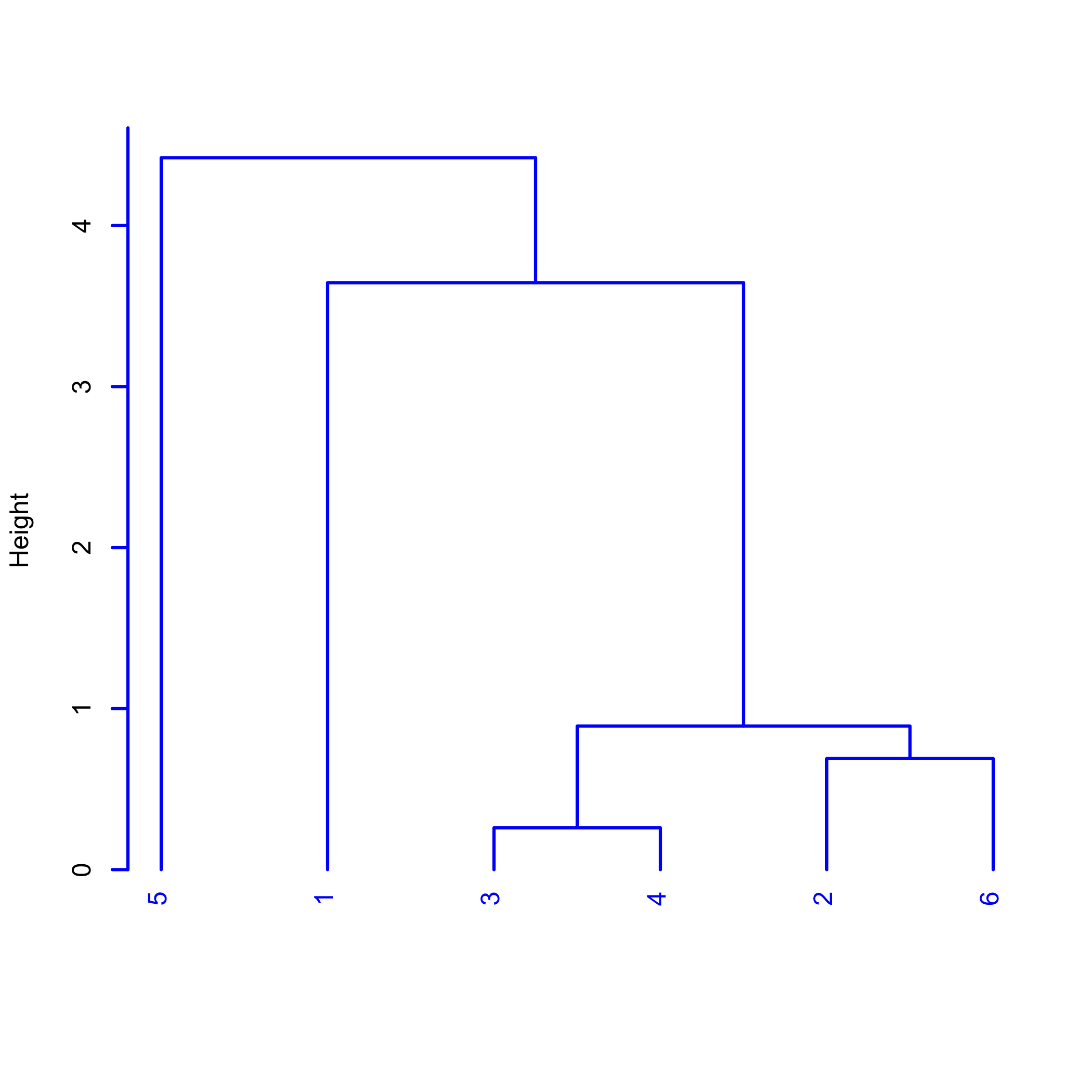
Як ми інтерпретуємо результати кластерного аналізу?

Кластерний аналіз зразків 24 з малюнка 11.1.1 показаний на малюнку з $\PageIndex{5}$ використанням 40 однаково розташованих довжин хвиль. На цій діаграмі ми можемо багато чого дізнатися про структуру цих зразків, яку ми можемо розділити на три окремі кластери зразків, як показано у коробках. Зразки в кожному кластері більше схожі один на одного, ніж зразки в інших кластерах. Одне з можливих пояснень цієї структури полягає в тому, що зразки 24 складаються з трьох аналітів, де для кожного кластера один з аналітів присутній у більшій концентрації, ніж два інших аналіти.

Малюнок $\PageIndex{5}$ : Кластерний аналіз 24 зразків з малюнка 11.1.1. Коробки поділяють 24 зразки на три різні кластери.