11.3: Аналіз основних компонентів

На малюнку нижче, який за структурою схожий на рисунок 11.2.2, але з більшою кількістю зразків - показує значення поглинання для зразків 80 на довжині хвиль 400.3 нм, 508,7 нм та 801,8 нм. Хоча осі визначають простір, в якому з'являються точки, самі окремі точки, за деякими винятками, не вирівняні з осями. Хмара 80 точок має глобальне середнє положення в цьому просторі і глобальну дисперсію навколо середнього глобального (див. Розділ 7.3, де ми використовували ці терміни в контексті аналізу дисперсії).

Малюнок\(\PageIndex{1}\): Графік розсіювання, що показує значення поглинання для 80 зразків на трьох довжині хвиль: 400.3 нм, 508,7 нм та 801,8 нм. На малюнку 11.2.2 показана підмножина цих даних за допомогою 24 зразків із 80 зразків.

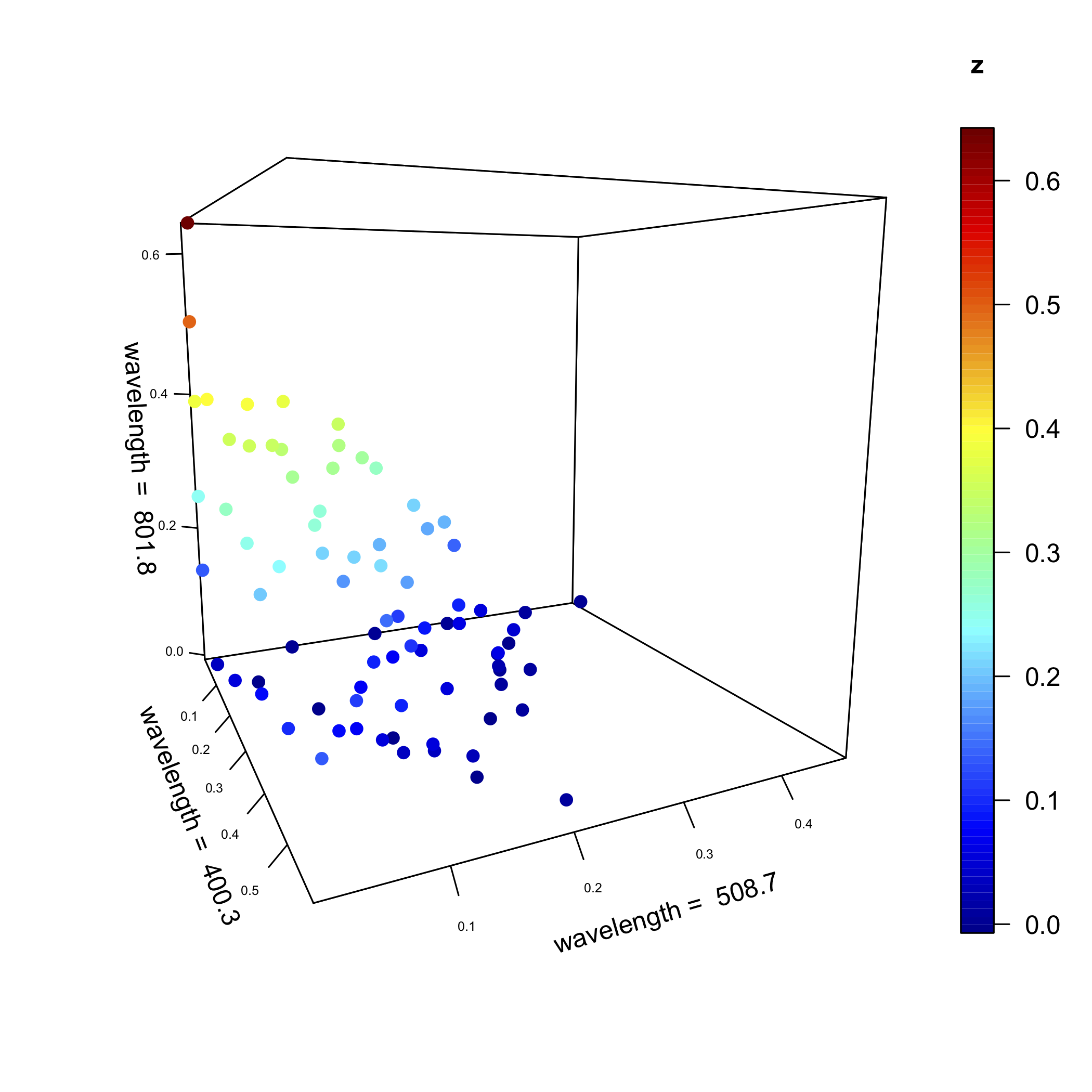
Припустимо, ми залишаємо точки в просторі такими, якими вони є, і обертаємо три осі. Ми можемо обертати три осі, поки одна не пройде крізь хмару таким чином, що максимізує зміну даних уздовж цієї осі, що означає, що ця нова вісь приносить найбільший внесок у глобальну дисперсію. Вирівнявши цю первинну вісь з даними, ми утримуємо її на місці і обертаємо інші дві осі навколо первинної осі, поки одна з них не пройде крізь хмару таким чином, щоб максимізувати залишкову дисперсію даних вздовж цієї осі; це стає вторинною віссю. Нарешті, третинна вісь залишилася третинна, що пояснює будь-яку дисперсію. По суті, це те, що включає в себе аналіз основних компонентів (PCA).

Як працює аналіз основних компонентів?

Однією з проблем розуміння того, як працює PCA, є те, що ми не можемо візуалізувати наші дані в більш ніж трьох вимірах. Дані на малюнку\(\PageIndex{1}\), наприклад, складаються з спектрів для 24 зразків, записаних на 635 довжині хвиль. Для візуалізації всіх цих даних потрібно побудувати їх уздовж 635 осей у 635 вимірному просторі! Розглянемо набагато простішу систему, яка складається з 21 вибірки, для кожного з яких ми вимірюємо відразу два властивості, які ми будемо називати першою змінною і другою змінною. \(\PageIndex{2}\)На малюнку показані наші дані, які ми можемо висловити як матрицю з 21 рядками, по одному для кожного з 21 зразків, і 2 стовпці, по одному для кожної з двох змінних.

\[ [D]_{21 \times 2} \nonumber \]

Малюнок\(\PageIndex{2}\): Графік розсіювання наших 21 зразків як функція їх значень для першої змінної та другої змінної.

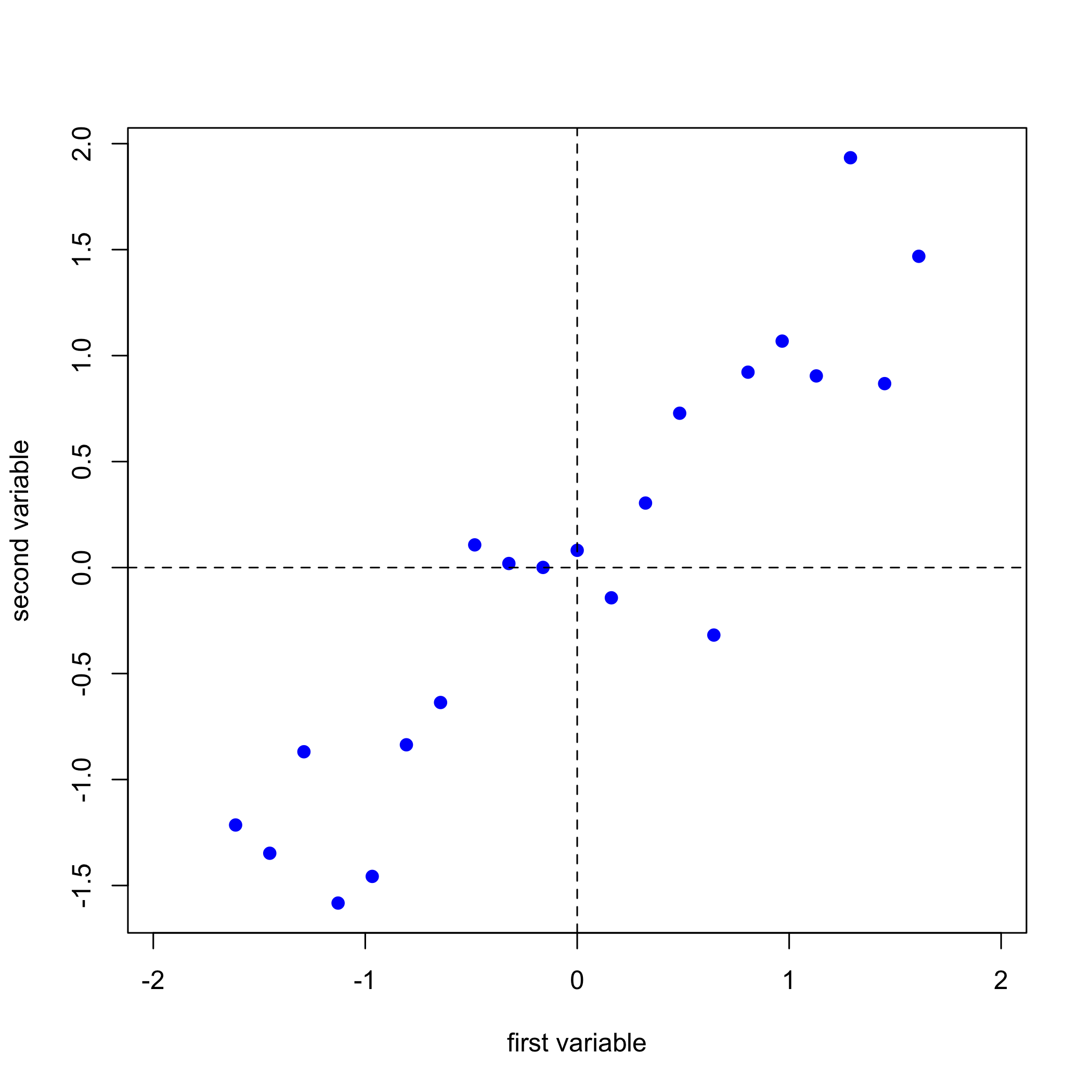
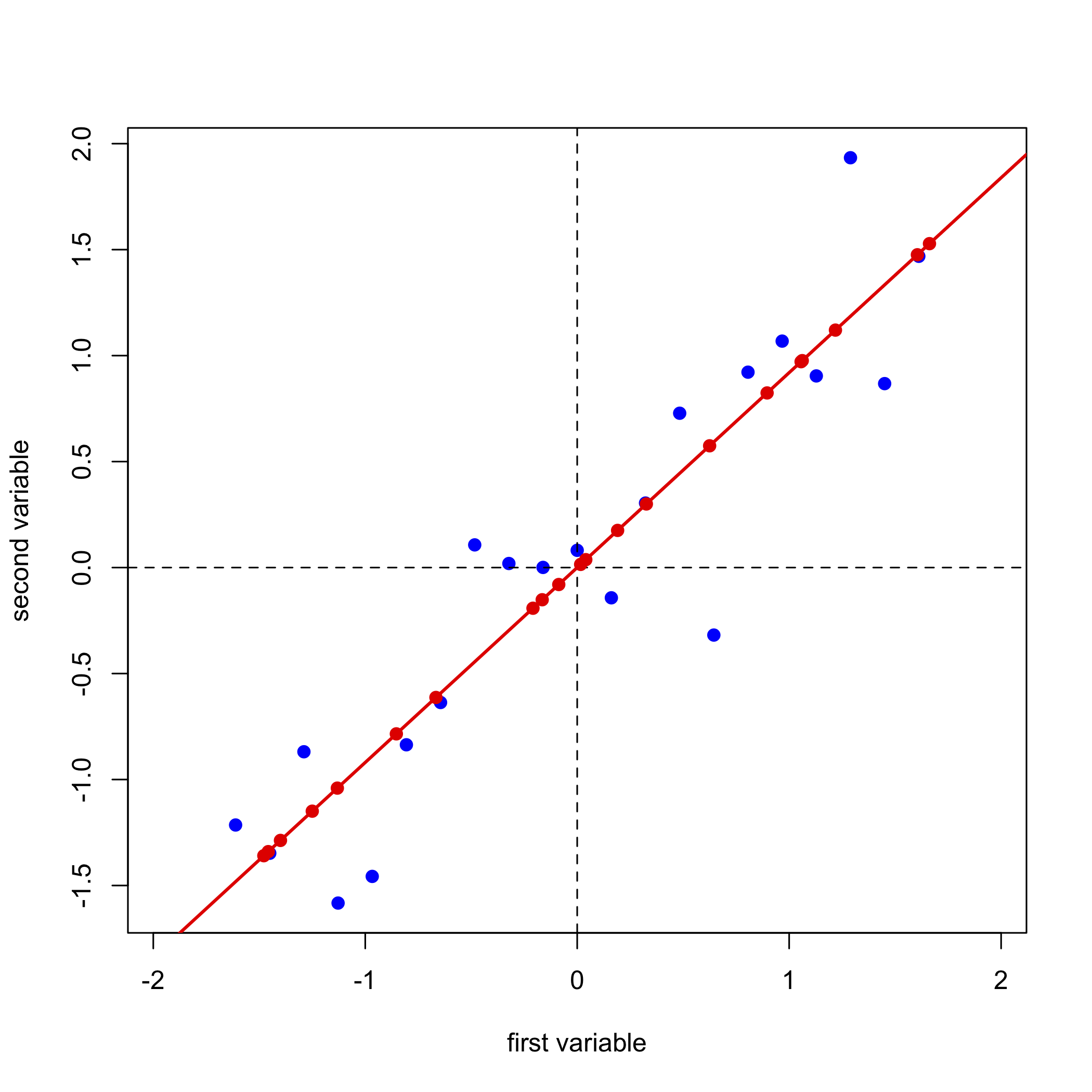
Далі ми завершуємо лінійний регресійний аналіз даних і додаємо лінію регресії до графіка; ми називаємо це першим основним компонентом.

Рисунок\(\PageIndex{3}\): Дані з малюнка, що\(\PageIndex{2}\) показують лінію регресії, яка є першою віссю головного компонента.

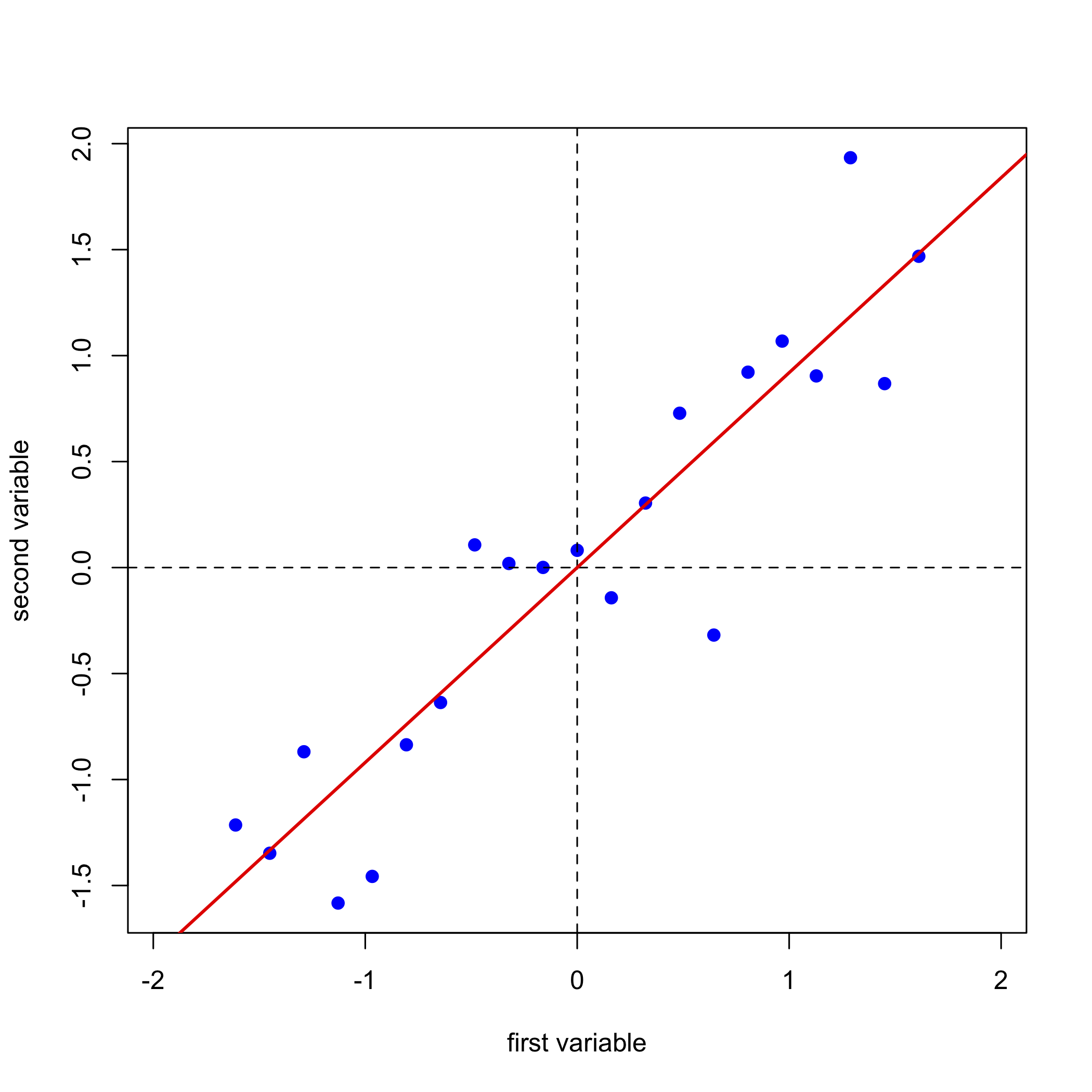
Проектування наших даних (синіх точок) на лінію регресії (червоні точки) дає розташування кожної точки на осі першого основного компонента; ці значення називаються балами,\(S\). Косинуси кутів між віссю першої головної складової та початковими осями називаються навантаженнями,\(L\). Ми можемо виразити зв'язок між даними, балами та навантаженнями за допомогою матричних позначень. Зверніть увагу, що з розмірів матриць для\(D\)\(S\), і\(L\), кожен з 21 зразків має оцінку і кожна з двох змінних має навантаження.

\[ [D]_{21 \times 2} = [S]_{21 \times 1} \times [L]_{1 \times 2} \nonumber\]

Малюнок\(\PageIndex{4}\): Проекції (червоні точки) на першу головну складову осі вихідних даних (сині точки) забезпечують оцінки, які є мірою відстані проекцій від початку.

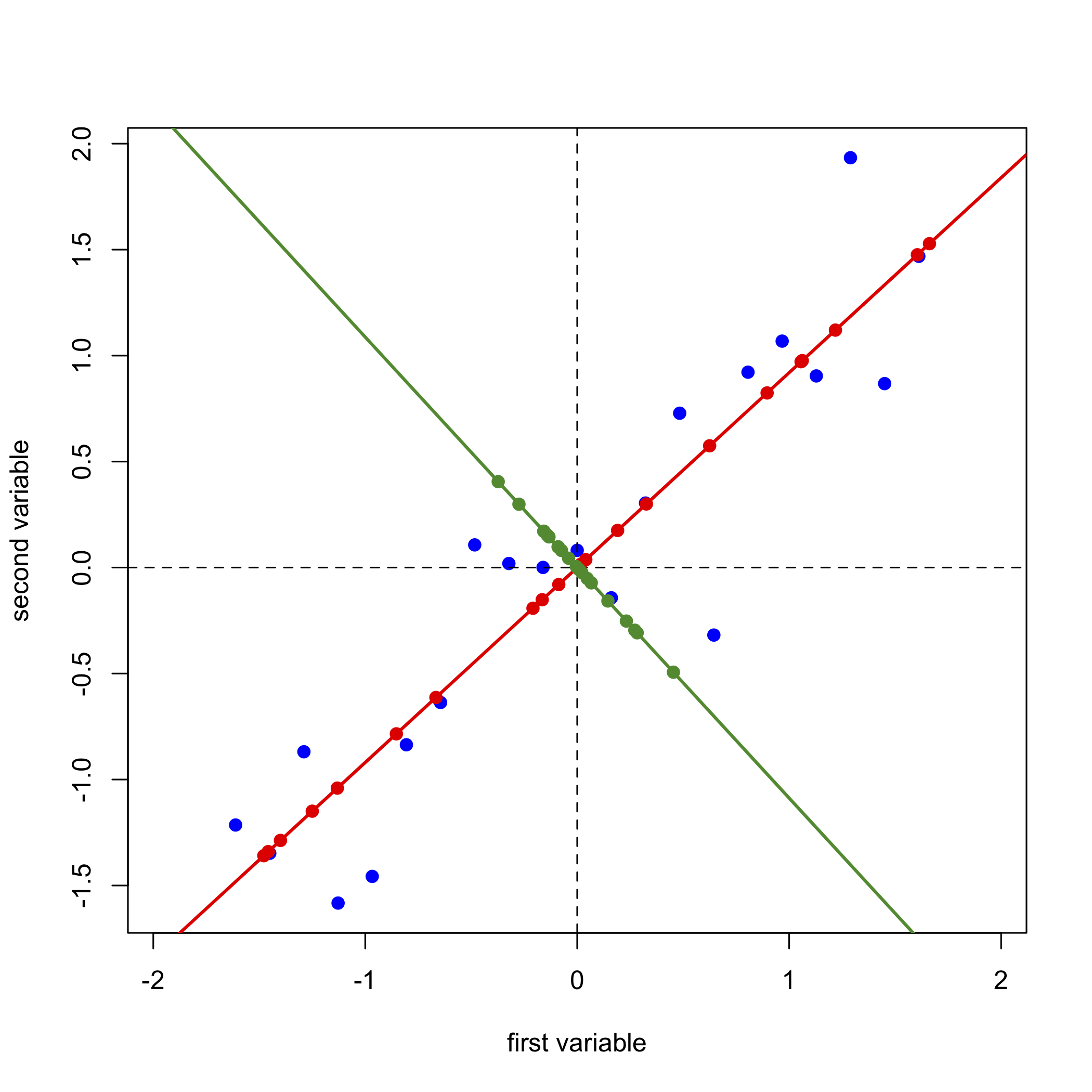
Далі ми проводимо лінію, перпендикулярну перпендикулярній осі першої головної складової, яка стає другою (і останньою) віссю головного компонента, проектуємо вихідні дані на цю вісь (точки зеленим кольором) і записуємо оцінки та навантаження для другого основного компонента.

\[ [D]_{21 \times 2} = [S]_{21 \times 2} \times [L]_{2 \times 2} \nonumber\]

Примітка

При множенні матриці кількість стовпців у першій матриці має дорівнювати числу рядків у другій матриці. Результатом множення матриці є нова матриця, яка має кількість рядків, рівних рядків першої матриці, і яка має кількість стовпців, рівну значенню другої матриці; таким чином множимо разом матрицю, яка є\(5 \times 4\) з одним, що\(4 \times 8\) дає матрицю, яка є\(5 \times 8\).

Рисунок\(\PageIndex{5}\): Проекції (зелені крапки) вихідних даних (сині крапки) на другу і кінцеву осі головного компонента.

Якби ми працювали з 21 зразками і 10 змінними, то ми б зробили так:

1. побудова даних для 21 вибірки в 10-вимірному просторі, де кожна змінна є віссю
2. знайти вісь першого основного компонента та записати оцінки та навантаження
3. проектувати точки даних для 21 зразків на 9-мірну поверхню, перпендикулярну осі першого основного компонента
4. знайти вісь другого основного компонента та записати оцінки та завантаження
5. проектувати точки даних для 21 зразків на 8-мірну поверхню, перпендикулярну осі другого (і першого) головного компонента
6. повторювати до тих пір, поки всі 10 основних компонентів не будуть ідентифіковані і всі оцінки та навантаження не повідомлені

Як ми інтерпретуємо результати аналізу основних компонентів?

Результати аналізу головної складової наведено балами та навантаженнями. Повернемося до даних з малюнка\(\PageIndex{1}\), але щоб зробити речі більш керованими, ми будемо працювати лише з 24 з 80 зразків і розширити кількість довжин хвиль від трьох до 16 (число, яке все ще є невеликою підмножиною 635 довжин хвиль, доступних нам). На малюнку нижче показані повні спектри для цих 24 зразків та конкретні довжини хвиль, які ми будемо використовувати як пунктирні лінії; Таким чином, наші дані - це матриця з 24 рядками та 16 стовпцями\([D]_{24 \times 16}\). Аналіз основних компонентів цих даних дасть 16 основних осей компонентів.

Малюнок\(\PageIndex{6}\): Спектри для 24 зразків. Пунктирні лінії показали 16 окремих довжин хвиль, які становлять 380,5 нм, 414,9 нм, 449,3 нм, 483,7 нм, 517,9 нм, 5506 нм, 538,2 нм, 613,3 нм, 642,9 нм, 672,7 нм, 703,3 нм, 735,5 нм, 767,8 нм, 800,2 нм, 832,6 нм та 868,6 нм. Це ті самі дані, які використовуються для ілюстрації кластерного аналізу.

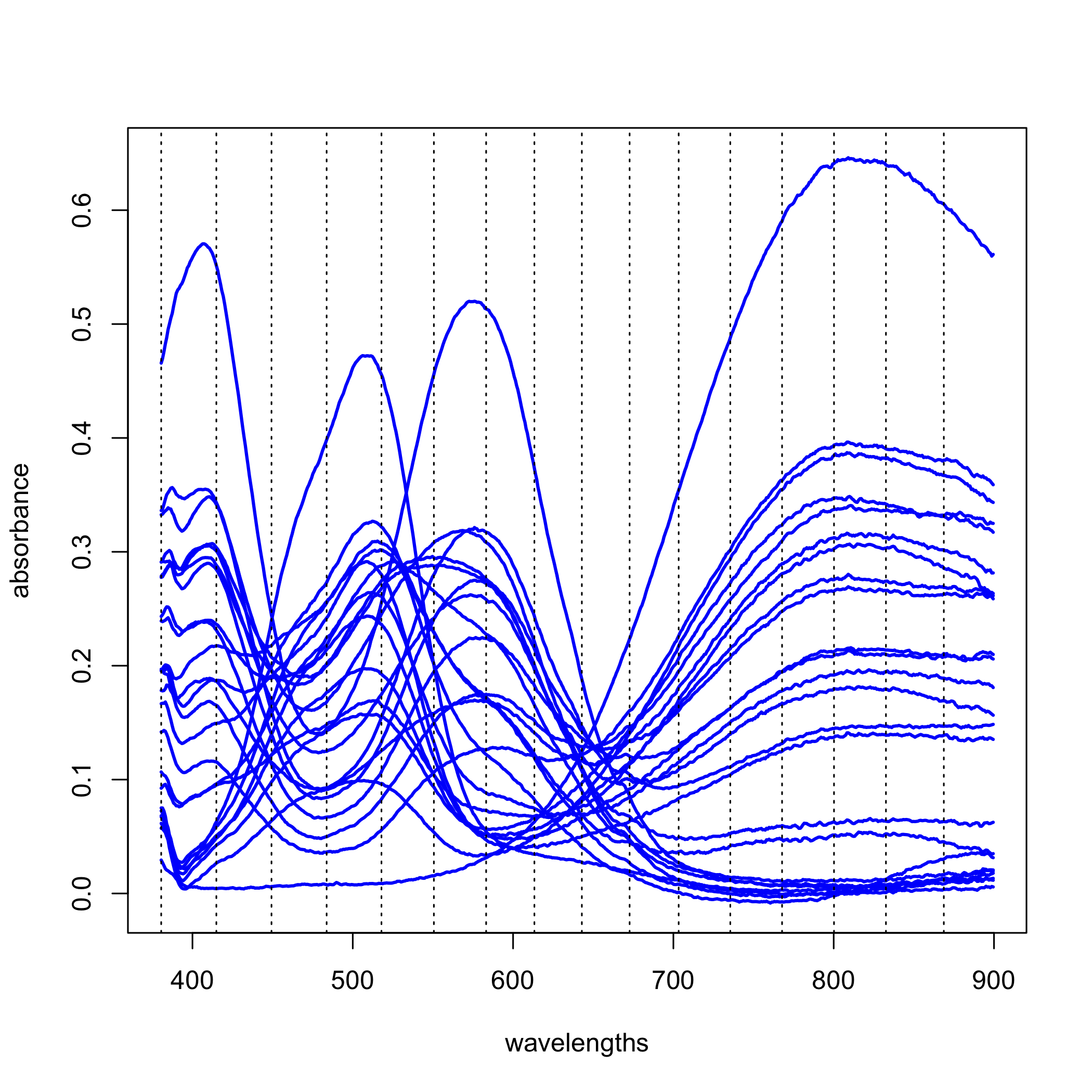
Кожен основний компонент припадає на частину загальних відхилень даних, і кожен наступний основний компонент становить меншу частку загальної дисперсії, ніж попередній основний компонент. Ті основні компоненти, які враховують незначні пропорції загальної дисперсії, імовірно, представляють шум у даних; решта основних компонентів імовірно є визначальними та достатніми для пояснення даних. Наступна таблиця містить резюме частки загальної дисперсії, поясненої кожним з 16 основних компонентів.

Таблиця\(\PageIndex{1}\): Частка загальної дисперсії, пояснена основними компонентами для даних на малюнку\(\PageIndex{6}\).

	ШТ. 1	ШТ/2	ШТ/3	ШТ. 4	ШТ/5	ШТ/6	ШТ/7	ШТ. 8
стандартне відхилення	3.3134	2.1901	0,42561	0,17585	0.09384	0.04607	0.04026	0.01253
частка дисперсії	0.6862	0,2998	0.01132	0,00193	0.00055	0.00013	0.00010	0,00001
сукупна пропорція	0.6862	0,9859	0,99725	0.99919	0,99974	0,99987	0,9997	0.9998
	ШТ/9	ШТ/10	ШТ 11	ШТ/12	ШТ/13	ШТ/14	ШТ/15	ШТ/16
стандартне відхилення	0,01049	0,009211	0.007084	0,004478	0,00416	0,003039	0,002377	0,001504
частка дисперсії	0,00001	0,000010	0,000000	0,000000	0,000000	0,000000	0,000000	0,000000
сукупна пропорція	0,9999	0,99990	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000

На перший основний компонент припадає 68,62% загальної дисперсії, а на другий основний компонент припадає 29,98% загальної дисперсії. У сукупності ці два основні компоненти складають 98,59% загальної дисперсії; додавання третього компонента становить понад 99% загальної дисперсії. Зрозуміло, що нам потрібно розглянути принаймні дві складові (можливо, три), щоб пояснити дані на малюнку\(\PageIndex{1}\). Решта 14 (або 13) основних компонентів просто враховують шум у вихідних даних. Це залишає нам наступне рівняння, що стосується вихідних даних з оцінками та навантаженнями:

\[ [D]_{24 \times 16} = [S]_{24 \times n} \times [L]_{n \times 16} \nonumber \]

де\(n\) - кількість компонентів, необхідних для пояснення даних, в даному випадку два-три.

Щоб більш уважно вивчити основні компоненти, ми будуємо бали для PC1 проти балів для PC2, щоб дати графік балів, показаний нижче, який показує оцінки, що займають простір трикутної форми.

Рисунок\(\PageIndex{7}\): Графік балів для 24 зразків, що показують їх оцінки вздовж осі першого основного компонента та осі другого основного компонента.

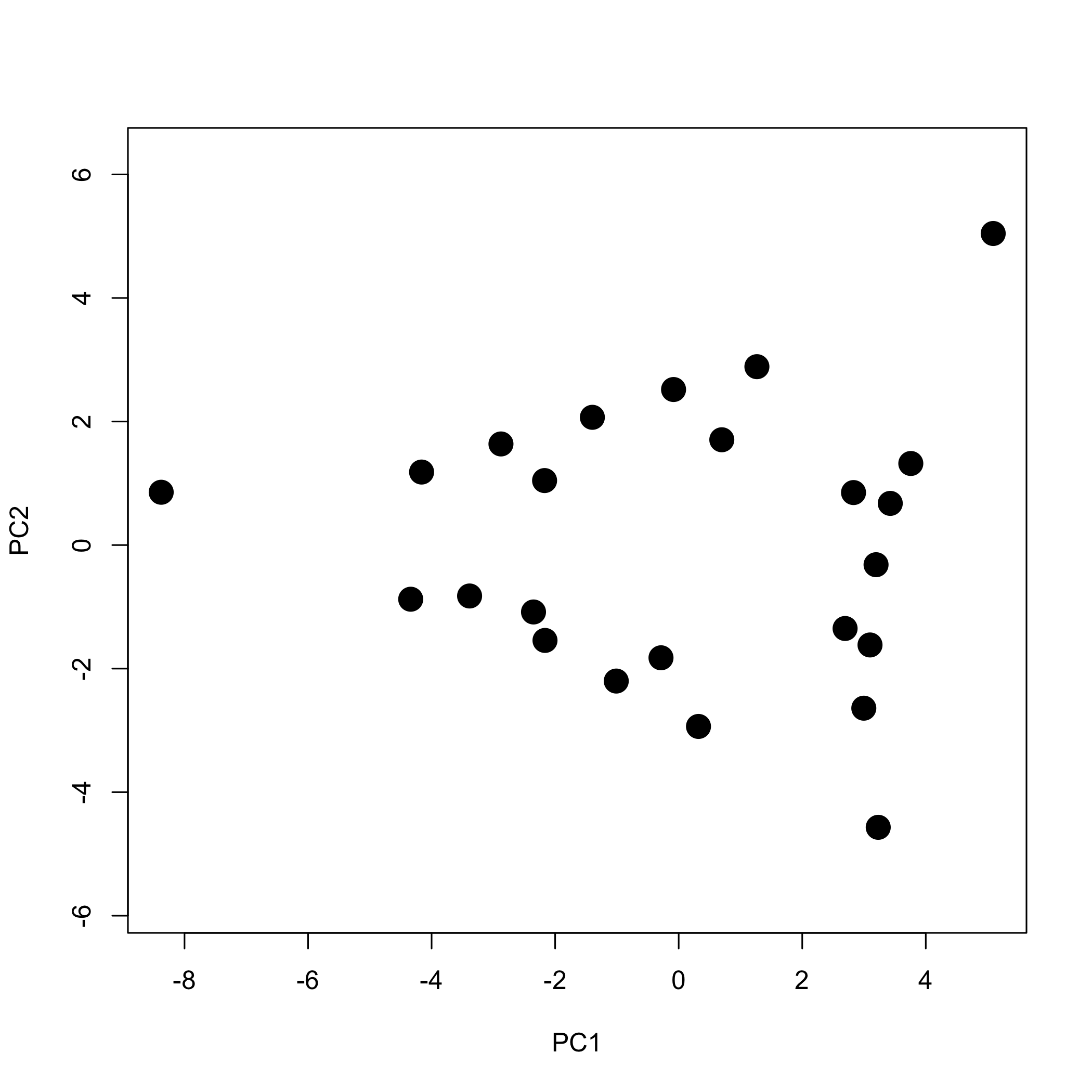
Оскільки наші дані є видимими спектрами, корисно порівняти рівняння

\[ [D]_{24 \times 16} = [S]_{24 \times n} \times [L]_{n \times 16} \nonumber \]

до закону Пива, який у матричній формі

\[ [A]_{24 \times 16} = [C]_{24 \times n} \times [\epsilon b]_{n \times 16} \nonumber \]

де\([A]\) дає значення поглинання для зразків 24 на довжині хвиль 16,\([C]\) дає концентрації двох або трьох компонентів, що складають зразки, і\([\epsilon b]\) дає продукти молярної поглинання та довжини шляху для кожного з двох або трьох компонентів на кожному з 16 довжин хвиль. Порівняння цих двох рівнянь свідчить про те, що оцінки пов'язані з концентраціями\(n\) компонентів і що навантаження пов'язані з молярною поглинанням\(n\) компонентів. Крім того, ми можемо пояснити закономірність балів на малюнку,\(\PageIndex{7}\) якщо кожен із 24 зразків складається з аналітів 1—3, причому три вершини є зразками, які містять один компонент кожна, зразки, що падають більш-менш на лінію між двома вершинами, є бінарними сумішами трьох аналітів, а решта точок є потрійними сумішами трьох аналітів.

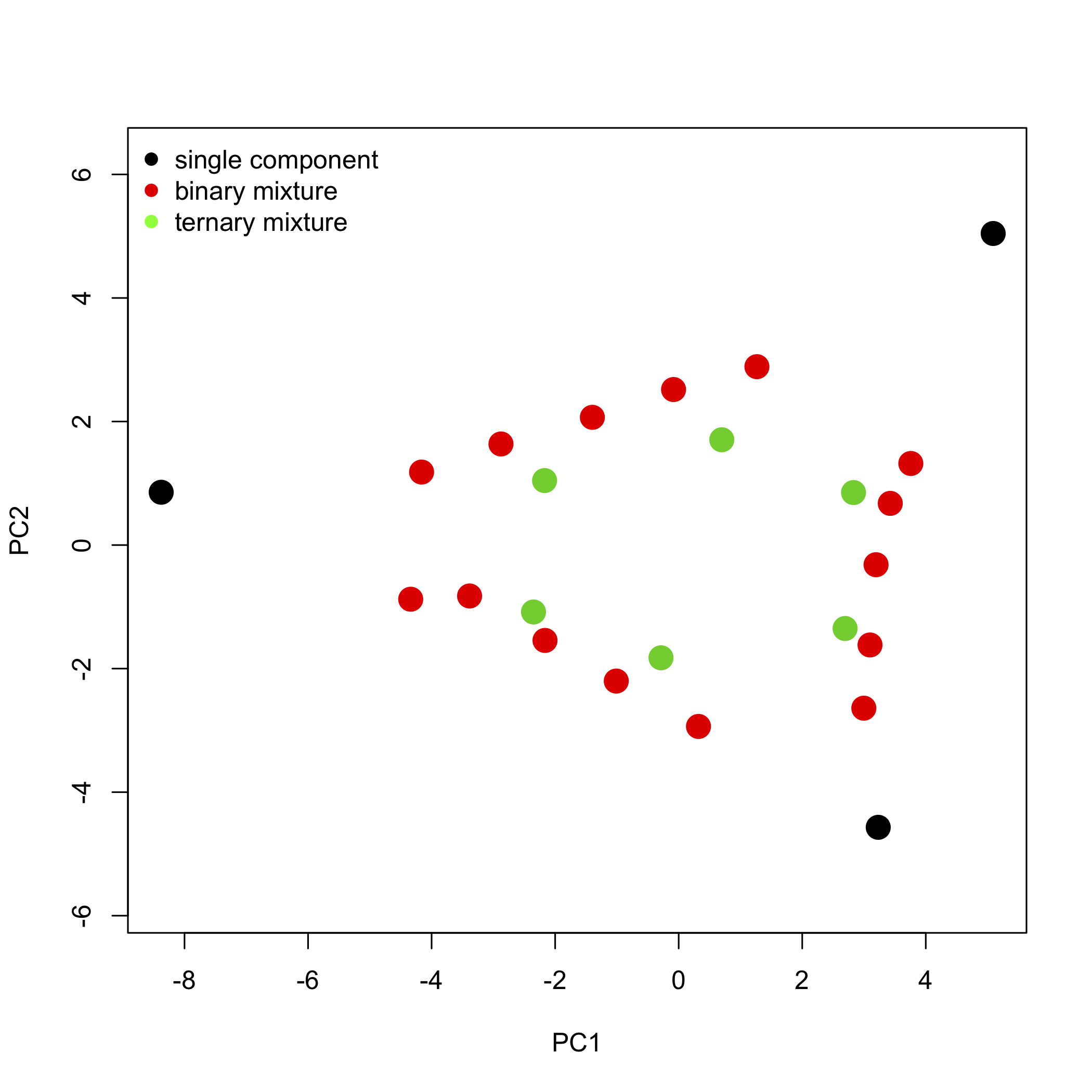
Рисунок\(\PageIndex{8}\): Графік балів з малюнка, кодований\(\PageIndex{7}\) кольором, щоб показати зразки, що містять один компонент, зразки, що містять два компоненти, та зразки, що містять три компоненти. Зверніть увагу, що бінарні суміші падають уздовж лінії (або плавно згинається дуги), яка з'єднує два однокомпонентні зразки, і що потрійні суміші займають внутрішній внутрішній простір, який визначається однокомпонентними зразками та бінарними сумішами.

Примітка

Якщо в наших 24 зразках є три компоненти, чому двох компонентів достатньо, щоб скласти майже 99% надмірної дисперсії? Припустимо, ми підготували кожен зразок, використовуючи об'ємну цифрову піпетку, щоб об'єднати разом аліквоти, витягнуті з розчинів чистих компонентів, розбавляючи кожен до фіксованого об'єму в об'ємній колбі об'ємом 10,00 мл. Наприклад, щоб зробити потрійну суміш, ми могли б піпет в 5,00 мл першого компонента і 4,00 мл компонента два. Якщо ми розводимо до кінцевого обсягу 10 мл, то обсяг третього компонента повинен бути менше 1,00 мл, щоб дати можливість розведення до позначки. Оскільки обсяг третього компонента обмежений обсягами перших двох компонентів, для пояснення більшості даних достатньо двох компонентів.

Навантаження, як зазначалося вище, пов'язані з молярною поглинанням компонентів нашого зразка, надаючи інформацію про довжині хвиль видимого світла, які найбільш сильно поглинаються кожним зразком. Ми можемо накладати графік навантажень на наш графік балів (це називається біплотом), як показано тут.

Малюнок\(\PageIndex{9}\): Біплот показує оцінки (точки) та навантаження (стрілки) для наших 24 зразків та 16 довжин хвиль. Положення навантажень щодо балів дає інформацію про взаємозв'язок між ними. Наприклад, навантаження для довжини хвилі 703,3 нм майже ідеально вирівнюється з оцінками для зразка 1, припускаючи, що ця довжина хвилі поглинається по суті лише єдиним компонентом, що становить цей зразок. Світло з довжиною хвилі 642.9 нм, однак, має навантаження, яке потрапляє між балами для зразків 1 і 2, припускаючи, що він поглинається єдиним компонентом, що становить зразок 1, і єдиним компонентом, що становить зразок 2.

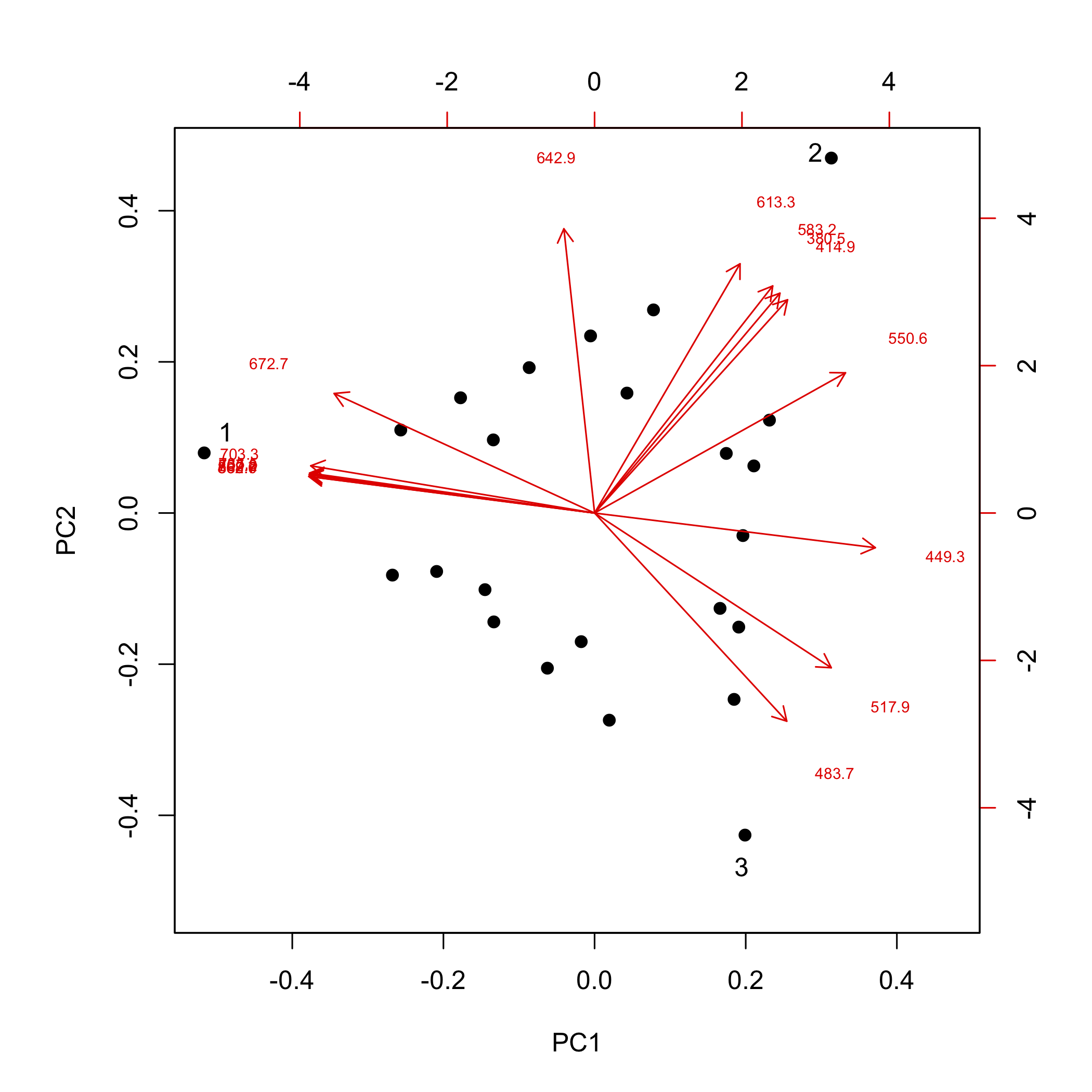
Кожна стрілка ототожнюється з однією з наших 16 довжин хвиль і вказує на комбінацію PC1 і PC2, з якою вона найбільш сильно пов'язана. Наприклад, хоча тут важко читати, всі довжини хвиль від 672,7 нм до 868,7 нм (повний перелік довжин хвиль див. підпис до малюнка\(\PageIndex{6}\)) міцно пов'язані з аналітом, який становить однокомпонентний зразок, ідентифікований номером один, і довжинами хвиль 380,5 нм, 414. 9 нм, 583,2 нм та 613,3 нм міцно пов'язані з аналітом, який становить однокомпонентний зразок, ідентифікований номером два.

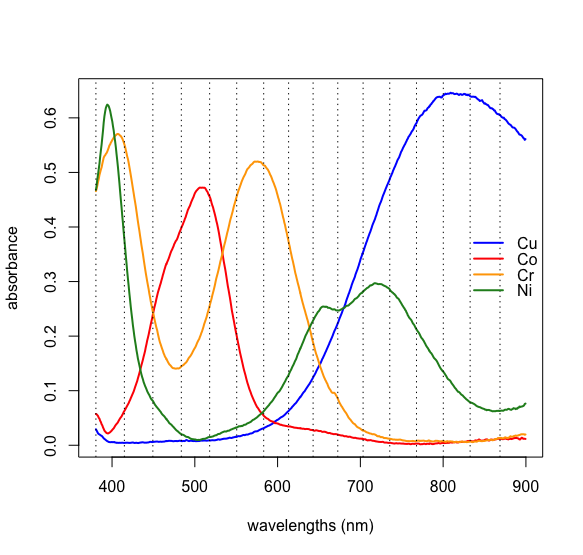
Якщо ми маємо певні знання про можливе джерело аналітів, то ми можемо зіставити експериментальні навантаження з аналітами. Зразки на малюнку\(\PageIndex{1}\) виготовлені з використанням розчинів декількох іонів перехідних металів першого ряду. \(\PageIndex{10}\)На малюнку показані видимі спектри для чотирьох таких іонів металів. Порівняння цих спектрів із навантаженнями на малюнку\(\PageIndex{9}\) показує, що Cu ²⁺ поглинає на тих довжині хвиль, найбільш пов'язаних із зразком 1, що Cr ^{3 +} поглинає на тих довжині хвиль, найбільш пов'язаних із зразком 2, і що Co ^{2 +} поглинає на довжині хвиль, найбільш пов'язаних із зразком 3; останній з іонів металу, Ni ^{2 +}, відсутній у зразках

Рисунок\(\PageIndex{10}\): Видимі спектри для чотирьох іонів металів, які можуть бути в 24 зразках. З цих іонів металів Ni ^{2 +} (aq) в зразках немає.