16.17: Огляд хімічної кінетики
- Page ID
- 24868
Положення рівноваги реакції визначає ступінь, в якій може відбутися реакція. Наприклад, ми очікуємо реакції з великою постійною рівноваги, наприклад, дисоціація HCl у воді
\[\ce{HCl}(aq) + \ce{H2O}(l) \ce{->} \ce{H3O+}(aq) + \ce{Cl-}(aq) \nonumber\]
приступити майже до завершення. Велика константа рівноваги, однак, не гарантує, що реакція досягне свого рівноважного положення. Багато реакцій з великими константами рівноваги, такі як зменшення\(\ce{MnO4-}\) на\(\ce{H2O}\)
\[\ce{4 MnO4-}(aq) + \ce{2 H2O}(l) \ce{->} \ce{4 MnO2}(s) + \ce{3 O2}(g) + \ce{4 OH-}(aq) \nonumber\]
не зустрічаються в помітному ступені. Вивчення швидкості, з якою хімічна реакція наближається до свого положення рівноваги, називається кінетикою.
Швидкість хімічних реакцій
Дослідження кінетики реакції починається з вимірювання швидкості її реакції. Розглянемо, наприклад, загальну реакцію, наведену нижче, із залученням водних розчинів A, B, C та D зі стехіометріями a, b, c та d.
\[a \ce{A} + b \ce{B} \ce{<=>} c \ce{C} + d \ce{D} \label{16.1}\]
Швидкість, або швидкість, з якою ця реакція наближається до свого рівноважного положення, визначається наступним зміною концентрації одного реагенту або одного продукту в залежності від часу. Наприклад, якщо ми контролюємо концентрацію реагенту А, ми виражаємо швидкість як
\[R = - \frac {d[\ce{A}]} {dt} \label{16.2}\]
де R - виміряна швидкість, виражена у вигляді зміни концентрації А в залежності від часу. Оскільки концентрація реагенту зменшується з часом, ми включаємо негативний знак, щоб швидкість мала позитивне значення.
Ми також можемо визначити швидкість, слідуючи за зміною концентрації продукту в залежності від часу, який ми виражаємо як
\[R^{\prime} = + \frac {d[\ce{C}]} {dt} \label{16.3}\]
Норми, що визначаються шляхом моніторингу різних видів, не обов'язково мають однакове значення. Швидкість R в рівнянні\ ref {16.2} і швидкість\(R^{\prime}\) в Рівнянні\ ref {16.3} мають однакове значення, тільки якщо стехіометричні коефіцієнти A і C в реакції\ ref {16.1} ідентичні. Загалом, взаємозв'язок між ставками R і\(R^{\prime}\) є
\[R = \frac {a} {c} \times R^{\prime} \nonumber\]
Закон про ставку
Закон швидкості описує, як на швидкість реакції впливає концентрація кожного виду в реакційній суміші. Закон швидкості для Реакція\ ref {16.1} приймає загальну форму
де k - константа швидкості\(\alpha\), і\(\beta\),\(\gamma\),\(\delta\), і\(\epsilon\) є порядками реакції реакції для кожного виду, присутнього в реакції.
Є кілька важливих моментів щодо закону швидкості в Equation\ ref {16.4}. По-перше, швидкість реакції може залежати від концентрації як реагентів, так і продуктів, а також концентрації виду, який не з'являється в загальній стехіометрії реакції. Наприклад, види E в Equation\ ref {16.4} можуть бути каталізатором, який не відображається в загальній стехіометрії реакції, але який збільшує швидкість реакції. По-друге, порядок реакції для даного виду не обов'язково такий же, як його стехіометрія в хімічній реакції. Порядок реакції може бути додатним, від'ємним або нульовим, і може приймати ціле або неціле значення. Нарешті, загальний порядок реакції реакції - це сума індивідуальних порядків реакції для кожного виду. Таким чином, загальний порядок реакції для Equation\ ref {16.4} дорівнює\(\alpha + \beta +\gamma + \delta + \epsilon\).
Кінетичний аналіз обраних реакцій
У цьому розділі ми розглядаємо застосування кінетики до декількох простих хімічних реакцій, зосереджуючись на тому, як ми можемо використовувати інтегровану форму закону швидкості для визначення порядків реакцій. Крім того, розглянемо, як можна визначити нормований закон для більш складної системи.
Реакції першого порядку
Найпростіший випадок, який ми можемо лікувати, - це реакція першого порядку, при якій швидкість реакції залежить від концентрації лише одного виду. Найпростішим прикладом реакції першого порядку є необоротне термічне розкладання одного реагенту, який ми представляємо як
\[\ce{A} \ce{->} \text{products} \label{16.5}\]
з нормовим законом
\[R = - \frac {d[\ce{A}]} {dt} = k[\ce{A}] \label{16.6}\]
Найпростіший спосіб продемонструвати, що реакція першого порядку в А - подвоїти концентрацію А і відзначити вплив на швидкість реакції. Якщо спостережувана швидкість подвоюється, то реакція є першим порядком в А. Крім того, ми можемо вивести зв'язок між концентрацією A та часом шляхом перестановки рівняння\ ref {16.6} та інтеграції.
\[\frac {d[\ce{A}]} {[\ce{A}]} = -kdt \nonumber\]
\[\int_{[{A}]_0}^{[{A}]_t}\frac{1}{[A]}d[A] = - k \int_{o}^{t}dt \label{16.7}\]
Оцінка інтегралів у рівнянні\ ref {16.7} та перестановка
\[\ln \frac {[\ce{A}]_t} {[\ce{A}]_0} = -kt \label{16.8}\]
\[\ln [\ce{A}]_t = \ln [\ce{A}]_0 - kt \label{16.9}\]
показує, що для реакції першого порядку графік\(\ln[\ce{A}]_t\) проти часу є лінійним з нахилом - k і y -перехоплення\(\ln[\ce{A}]_0\). Рівняння\ ref {16.8} і рівняння\ ref {16.9} відомі як інтегровані форми закону швидкості. Реакція\ ref {16.5} не єдина можлива форма реакції першого порядку. Наприклад, реакція
\[\ce{A} + \ce{B} \ce{->} \text{products} \label{16.10}\]
буде слідувати кінетиці першого порядку, якщо реакція першого порядку в А і якщо концентрація В не впливає на швидкість реакції, що може статися, якщо механізм реакції включає принаймні два етапи. Уявіть, що на першому кроці A повільно перетворюється на проміжний вид С, який швидко реагує з рештою реагентом, B, в один або кілька кроків, утворюючи продукти.
\[\ce{A} \ce{->} \ce{B} (\text{slow}) \nonumber\]
\[\ce{B} + \ce{C} \ce{->} \text{products} \nonumber\]
Оскільки швидкість реакції залежить лише від цих видів на найповільнішому етапі - зазвичай називається кроком визначення швидкості - і будь-які попередні кроки, види B не з'являться в законі про швидкість.
Реакції другого порядку
Найпростіша реакція, що демонструє поведінку другого порядку, це
\[\ce{2 A} \ce{->} \text{products} \nonumber\]
для яких діє закон про ставки
\[R = - \frac {d[\ce{A}]} {dt} = k[\ce{A}]^2 \nonumber\]
Продовжуючи, як ми робили раніше для реакції першого порядку, ми можемо легко вивести інтегровану форму закону про ставки.
\[\frac {d[\ce{A}]} {[\ce{A}]^2} = -kdt \nonumber\]
\[\int_{[\ce{A}]_0}^{[\ce{A}]_t} = -k \int_0^t dt \nonumber\]
\[\frac {1} {[\ce{A}]_t} = kt + \frac {1} {[\ce{A}]_0} \nonumber\]
Отже, для реакції другого порядку ділянка ([A] t) —1 проти t є лінійним з нахилом k і a y -перехопленням ([A] 0) —1. Крім того, ми можемо показати, що реакція другого порядку в А, спостерігаючи вплив на швидкість при зміні концентрації А. У цьому випадку подвоєння концентрації А призводить до чотириразового збільшення швидкості реакції.
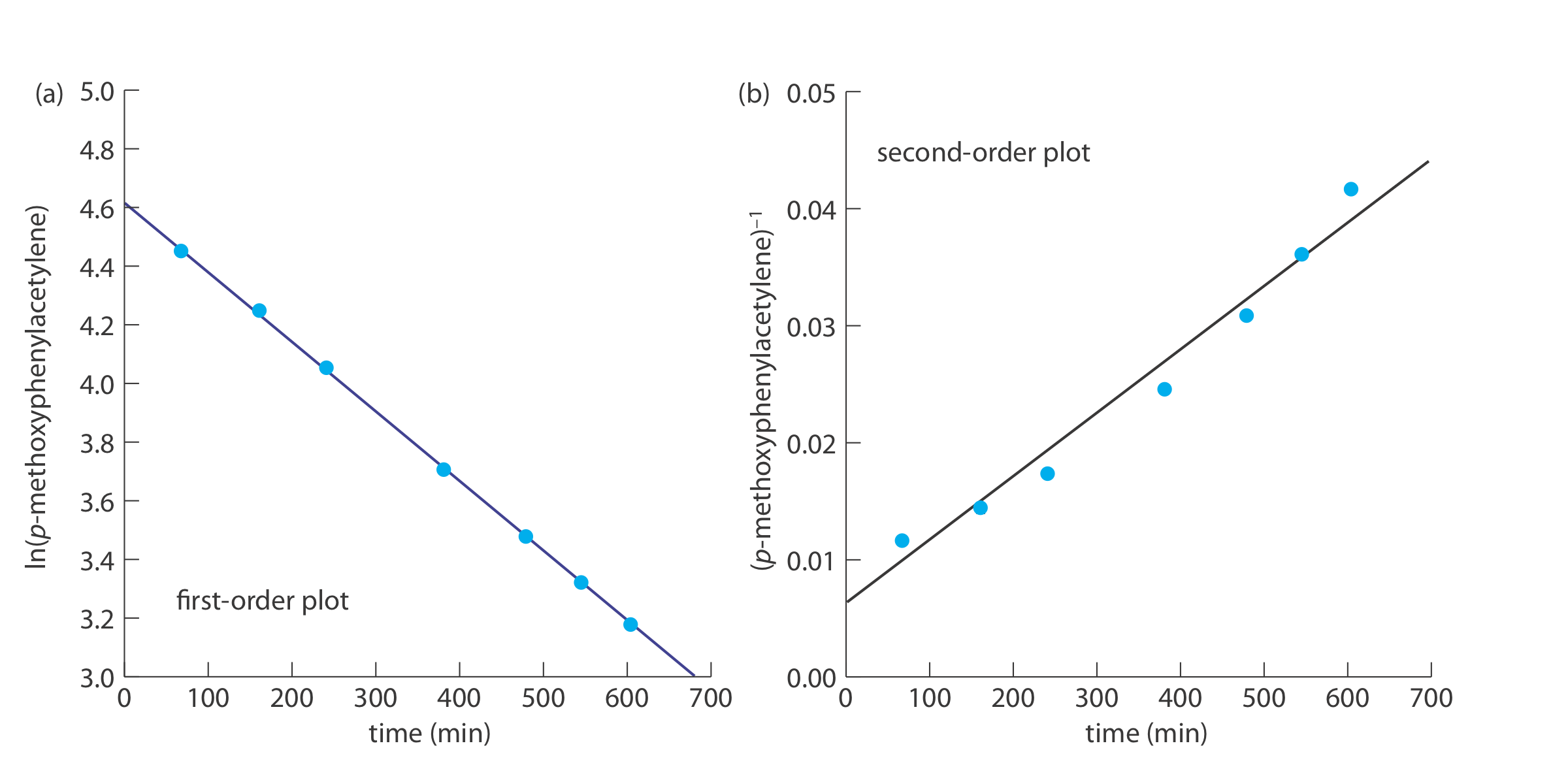
Наступні дані були отримані в ході кінетичного дослідження гідратації р -метоксифенілацетилену шляхом вимірювання відносних кількостей реагентів і продуктів за ЯМР [дані Кауфмана, D,; Sterner, C; Masek, B; Svenningsen, R.; Samuelson, GJ Chem. Едук. 1982, 59, 885—886].
| час (хв) | % п-метоксифенілацетилен |
|---|---|
| 67 | 85.9 |
| 161 | 70.0 |
| 241 | 57.6 |
| 381 | 40.7 |
| 479 | 32.4 |
| 545 | 27.7 |
| 604 | 24 |
Рішення
Для визначення порядку реакції ми плануємо ln (%p-метоксифенілацетилен) проти часу для реакції першого порядку, і (%p-метоксифенілацетилен) —1 проти часу реакції другого порядку (див. Нижче). Оскільки пряма лінія для графіка першого порядку добре відповідає даним, ми робимо висновок, що реакція першого порядку в р -мет- оксифенілацетилен. Зауважте, що коли ми будуємо дані за допомогою рівняння для реакції другого порядку, дані показують кривизну, яка не відповідає прямолінійній моделі.
Реакції псевдопорядку та метод початкових швидкостей
На жаль, більшість реакцій, що мають важливе значення в аналітичній хімії, не відповідають простим законам першого порядку або другого порядку, розглянутим вище. Ми частіше зустрічаємо закон швидкості другого порядку, заданий у Equation\ ref {16.11}, ніж у Equation\ ref {16.10}.
\[R = k [\ce{A}] [\ce{B}] \label{16.11}\]
Демонстрація того, що реакція підпорядковується закону швидкості в Equation\ ref {16.11} ускладнюється відсутністю простої інтегрованої форми закону ставок. Часто ми можемо спростити кінетику шляхом проведення аналізу в умовах, коли концентрації всіх видів, крім одного, настільки великі, що їх концентрації ефективно залишаються постійними під час реакції. Наприклад, якщо концентрація B вибрана така\([\ce{B}] >> [\ce{A}]\), то Equation\ ref {16.11} спрощує
\[R = k^{\prime} [\ce{A}] \nonumber\]
де константа швидкості k ⸺_ дорівнює k [B]. У цих умовах реакція, здається, слідує кінетиці першого порядку в А; з цієї причини ми ідентифікуємо реакцію як псевдо-першого порядку в А. Ми можемо перевірити порядок реакції для А, використовуючи або інтегрований закон швидкості, або спостерігаючи вплив на швидкість реакції зміни концентрації А. Щоб знайти порядок реакції для B, повторюємо процес в умовах, де\([\ce{A}] >> [\ce{B}]\).
Варіацією використання псевдовпорядкованих реакцій є метод початкової швидкості. У цьому підході ми проводимо серію експериментів, в яких ми змінюємо один за раз концентрацію кожного виду, що може вплинути на швидкість реакції і вимірювати отриману початкову швидкість. Порівняння початкової швидкості реакції для двох експериментів, в яких різна лише концентрація одного виду, дозволяє визначити порядок реакції для цього виду. Застосування цього методу викладено в наступному прикладі.
Наступні дані були зібрані в ході кінетичного дослідження йодації ацетону шляхом вимірювання концентрації не прореагував I 2 в розчині [дані Birk, J.P.; Walters, D.L. J. Chem. Едук. 1992, 69, 585—587].
| експеримент номер | \([\ce{C3H6O}]\)(М) | \([\ce{H3O+}]\)(М) | \([\ce{I2}]\)(М) | Швидкість (М с —1) |
|---|---|---|---|---|
| 1 | \ ([\ ce {C3H6O}]\) (М) ">1.33 | \ ([\ ce {H3O+}]\) (М) ">0.0404 | \ ([\ ce {I2}]\) (М) ">\(6.65 \times 10^{-3}\) | \(1.78 \times 10^{-6}\) |
| 2 | \ ([\ ce {C3H6O}]\) (М) ">1.33 | \ ([\ ce {H3O+}]\) (М) ">0.0809 | \ ([\ ce {I2}]\) (M)» клас = "лт-хім-135884">
\(6.65 \times 10^{-3}\) |
\(3.89 \times 10^{-6}\) |
| 3 | \ ([\ ce {C3H6O}]\) (М) ">1.33 | \ ([\ ce {H3O+}]\) (М) ">0.162 | \ ([\ ce {I2}]\) (М) ">\(6.65 \times 10^{-3}\) | \(8.11 \times 10^{-6}\) |
| 4 | \ ([\ ce {C3H6O}]\) (М) ">1.33 | \ ([\ ce {H3O+}]\) (М) ">0.323 | \ ([\ ce {I2}]\) (М) ">\(6.65 \times 10^{-3}\) | \(1.66 \times 10^{-5}\) |
| 5 | \ ([\ ce {C3H6O}]\) (М) ">0.167 | \ ([\ ce {H3O+}]\) (М) ">0.323 | \ ([\ ce {I2}]\) (М) ">\(6.65 \times 10^{-3}\) | \(1.64 \times 10^{-6}\) |
| 6 | \ ([\ ce {C3H6O}]\) (М) ">0.333 | \ ([\ ce {H3O+}]\) (М) ">0.323 | \ ([\ ce {I2}]\) (М) ">\(6.65 \times 10^{-3}\) | \(3.76 \times 10^{-6}\) |
| 7 | \ ([\ ce {C3H6O}]\) (М) ">0.667 | \ ([\ ce {H3O+}]\) (М) ">0.323 | \ ([\ ce {I2}]\) (М) ">\(6.65 \times 10^{-3}\) | \(7.55 \times 10^{-6}\) |
| 8 | \ ([\ ce {C3H6O}]\) (М) ">0.333 | \ ([\ ce {H3O+}]\) (М) ">0.323 | \ ([\ ce {I2}]\) (М) ">\(3.32 \times 10^{-3}\) | \(3.57 \times 10^{-6}\) |
Рішення
Порядок закону швидкості щодо трьох реагентів визначається шляхом порівняння швидкостей двох експериментів, в яких відбувається зміна концентрації тільки для одного з реагентів. Наприклад, в експериментах 1 і 2 тільки\([\ce{H3O+}]\) зміни; як подвоєння ставки\([\ce{H3O+}]\) подвоює, ми знаємо, що реакція першого порядку в\(\ce{H3O+}\). Працюючи таким же чином, експерименти 6 і 7 показують, що реакція також першого порядку по відношенню до\([\ce{C3H6O}]\), а Експерименти 6 і 8 показують, що швидкість реакції незалежнавід\([\ce{I2}]\). Таким чином, нормовим законом є
\[R = k [\ce{C3H6O}] [\ce{H3O+}] \nonumber\]
Для визначення значення константи швидкості підставляємо норму, та\([\ce{H3O+}]\), і\([\ce{H3O+}]\) для кожного експерименту в закон швидкості і вирішуємо для k. Використання даних з експерименту 1, наприклад, дає константу швидкості\(3.31 \times 10^{-5} \text{ M}^{-1} \text{ s}^{-1}\). Середня константа швидкості для восьми експериментів становить\(3.49 \times 10^{-5} \text{ M}^{-1} \text{ s}^{-1}\).
