16.16: Протиточні поділи
- Page ID
- 24869
У 1949 році Лайман Крейг запровадив вдосконалений метод поділу аналітів з аналогічними співвідношеннями розподілу [Craig, L.C. J. Biol. Хім. 1944, 155, 519—534]. Методика, яка відома як протитечічна рідина-рідка екстракція, викладена на малюнку Template:index і детально розглядається нижче. На відміну від послідовного екстракції рідини - рідини, в якій ми неодноразово витягуємо зразок, що містить аналіт, протипоточна екстракція використовує серійне вилучення як зразка, так і фаз екстракції. Хоча протиточні поділи більше не поширені - хроматографічні поділи набагато ефективніші з точки зору роздільної здатності, часу та простоти використання - теорія, що стоїть за вилученням протиструму, залишається корисною як введення в теорію хроматографічних поділів.
Для відстеження прогресу протиточного видобутку рідина-рідина нам потрібно прийняти конвенцію про маркування. Як показано на малюнку Template:index, на кожному етапі вилучення протиструму ми спочатку завершуємо вилучення, а потім передаємо верхню фазу на нову трубку, яка містить частину свіжої нижньої фази. Етапи маркуються послідовно, починаючи з нуля. Вилучення відбуваються в серії трубок, які також маркуються послідовно, починаючи з нуля. Верхня і нижня фази в кожній трубці ідентифікуються буквою і цифрою, при цьому букви U і L представляють відповідно верхню фазу і нижню фазу, і числом, що вказує на крок вилучення протитечії, в який вперше була введена фаза. Наприклад, U 0 - це верхня фаза, введена на етапі 0 (під час першої екстракції), а L 2 - нижня фаза, введена на етапі 2 (під час третьої екстракції). Нарешті, поділ аналіту в будь-якій екстракційній трубці призводить до того, що фракція р залишається у верхній фазі, а фракція q залишається в нижній фазі. Значення q обчислюються за допомогою рівняння\ ref {16.1}, яке ідентично рівнянню 7.7.6 у главі 7.
Дріб p, звичайно, дорівнює 1 — q. Зазвичай V aq і V org рівні в протитечії, хоча це не є вимогою.
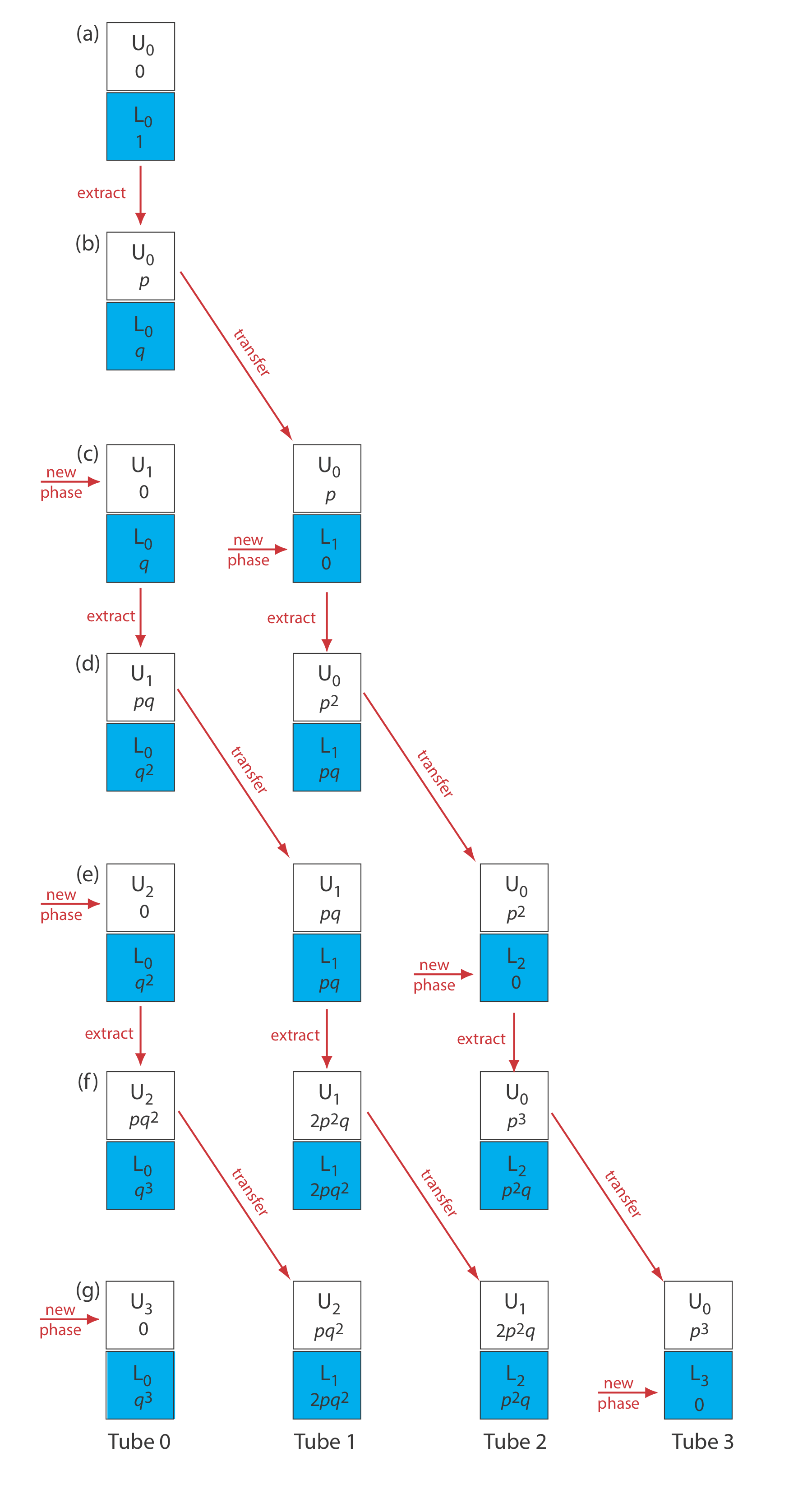
Припустимо, що аналіт, який ми хочемо виділити, присутній у водній фазі 1 М HCl, і що органічною фазою є бензол. Оскільки бензол має меншу щільність, він є верхньою фазою, а 1 М HCl - нижньою. Для початку вилучення протитечії поміщаємо водний зразок, який містить аналіт, в трубці 0 разом з рівним об'ємом бензолу. Як показано на малюнку\(\PageIndex{1}\text{a}\), перед вилученням весь аналіт присутній у фазі L 0. Коли екстракція завершена, як показано на малюнку\(\PageIndex{1}\text{b}\), частка р аналіту присутній у фазі U 0, а дріб q - у фазі L 0. На цьому крок 0 вилучення протитечії завершено. Якщо ми зупинимося на цьому, немає різниці між простою рідиною - видобутком рідини та вилученням протиструму.
Виконавши крок 0, знімаємо фазу U 0 і додаємо свіжу порцію бензолу, U 1, в трубку 0 (див. Рис.\(\PageIndex{1}\text{c}\)). Це теж ідентично простому видобутку рідина-рідина. Тут починається потужність вилучення протиструму - замість того, щоб відкладати фазу U 0, ми поміщаємо її в трубку 1 разом з порцією безаналітичного водного 1 M HCl як фази L 1 (див. Рис.\(\PageIndex{1}\text{c}\)). Пробка 0 тепер містить дріб q аналіту, а трубка 1 містить частку р аналіту. Завершення екстракції в пробірці 0 призводить до того, що частка р її вмісту залишається у верхній фазі, а частка q залишається в нижній фазі. Таким чином, фази U 1 і L 0 тепер містять відповідно дроби pq і q 2 від вихідної кількості аналіту. Слідуючи тій же логіці, легко показати, що фази U 0 і L 1 в трубці 1 містять відповідно фракції p 2 і pq аналіту. На цьому крок 1 видобутку завершено (див. Рис.\(\PageIndex{1}\text{d}\)). Як показано на залишку Figure Template:index, вилучення протиструму триває з цим циклом фазових переносів та вилучень.
У протиточному вилученні рідина-рідина нижня фаза в кожній трубці залишається на місці, а верхня фаза рухається від трубки 0 до послідовно вищих пронумерованих трубок. Ми визнаємо цю різницю в русі двох фаз, посилаючись на нижню фазу як стаціонарну фазу, а верхню - як рухому. З кожним перенесенням частина аналіту в трубці r переміщається в трубку\(r + 1\), в той час як частина аналіту в трубці\(r - 1\) переміщається в трубку r. Аналіт, введений в трубці 0, рухається з рухомою фазою, але зі швидкістю, яка повільніше рухомої фази, оскільки на кожному кроці частина аналіту переходить у стаціонарну фазу. Аналіт, який переважно витягується в стаціонарну фазу, витрачає пропорційно менше часу в рухомій фазі і рухається з повільнішою швидкістю. Зі збільшенням кількості кроків аналіти з різними значеннями q в кінцевому підсумку розділяються на абсолютно різні набори екстракційних трубок.
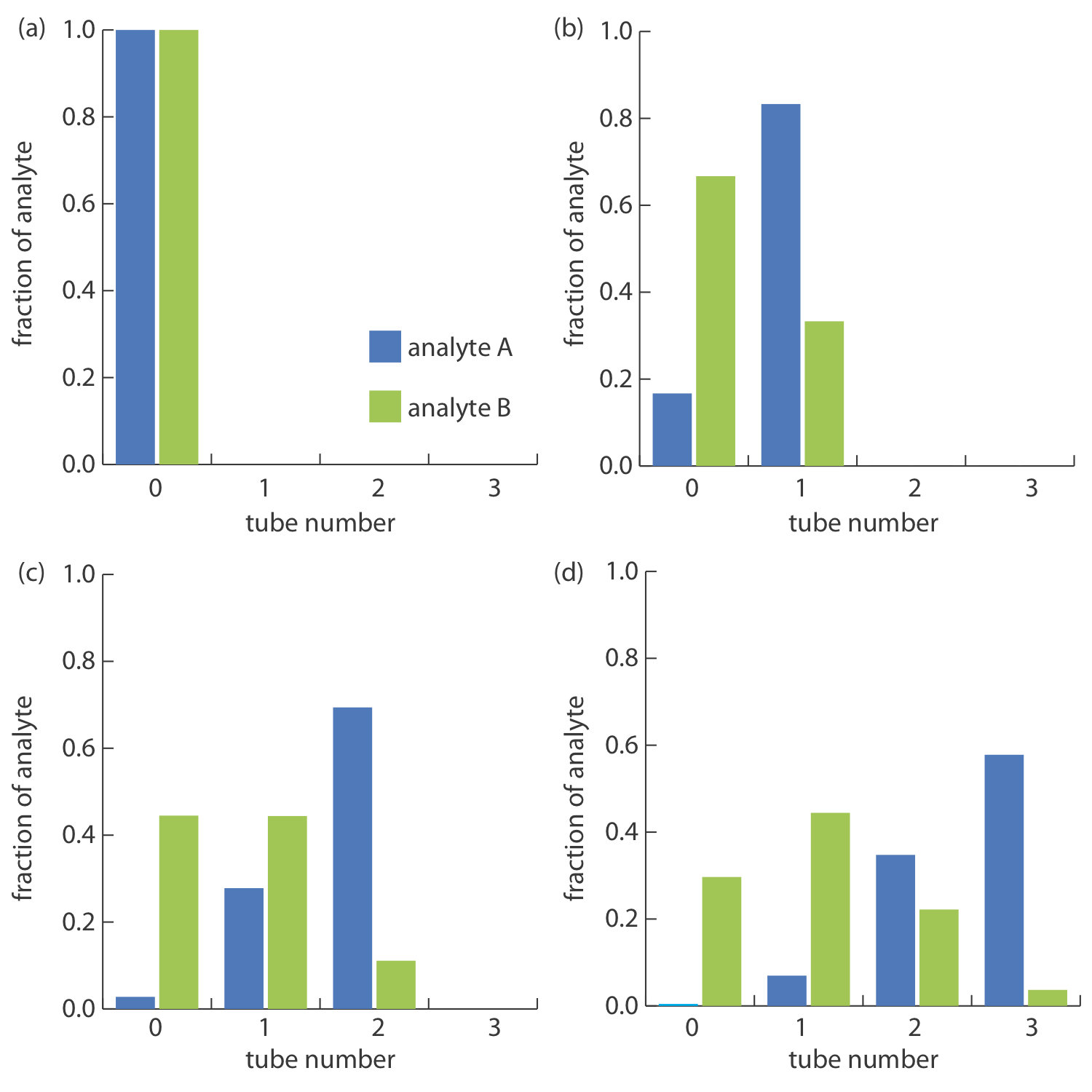
Про ефективність вилучення протиточного можна судити за допомогою гістограми, яка показує частку аналіту, присутнього в кожній трубці. Щоб визначити загальну кількість аналіту в екстракційній трубці, ми додаємо разом частку аналіту, присутній у верхній і нижній фазах трубки після кожного перенесення. Наприклад, на початку кроку 3 (див. Рис.\(\PageIndex{1}\text{g}\)) верхня і нижня фази трубки 1 містять фракції pq 2 і 2 pq 2 аналіта відповідно; таким чином, загальна частка аналіту в трубці дорівнює 3 pq 2. Таблиця Template:index підсумовує це для кроків, описаних на малюнку Template:index. Типова гістограма, розрахована за умови співвідношення розподілу 5,0 для аналіту А і 0,5 для аналіту B, показана на малюнку Template:index. Хоча чотирьох кроків недостатньо для розділення аналітів у цьому випадку, зрозуміло, що якщо ми продовжимо вилучення протиструму на додаткові трубки, ми врешті-решт відокремлюємо аналіти.
| \(\ce{n} \ce{v} \ce{r} \ce{->} \) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \ (\ ce {n}\ ce {v}\ ce {r}\ ce {-">}\) ">0 | 1 | — | — | — |
| \ (\ ce {n}\ ce {v}\ ce {r}\ ce {-">}\) ">1 | q | р | — | — |
| \ (\ ce {n}\ ce {v}\ ce {r}\ ce {-">}\) ">2 | q 2 | 2 шт. | р 2 | — |
| \ (\ ce {n}\ ce {v}\ ce {r}\ ce {-">}\) ">3 | q 3 | 3 шт | 3 п 2 кв | п 3 |
Рисунок Template:index та Таблиця Template:index показують, як змінюється розподіл аналіта під час перших чотирьох кроків вилучення протиструму. Тепер розглянемо, як ми можемо узагальнити ці результати для обчислення кількості аналіту в будь-якій трубці, на будь-якому етапі під час видобутку. Ви можете розпізнати закономірність записів у таблиці Template:index як наступний біноміальний розподіл
\[f(r, n) = \frac {n!} {(n - r)! r!} p^{r} q^{n - r} \label{16.2}\]
де f (r, n) - частка аналіту, присутня в трубці r на етапі n протиточного вилучення, причому верхня фаза містить частку\(p \times f(r, n)\) аналіту, а нижня фаза містить\(q \times f(r, n)\) частку аналіту.
Вилучення протиструму, показане на малюнку Template:index, здійснюється через крок 30. Обчисліть частку аналітів А і В в пробірках 5, 10, 15, 20, 25 і 30.
Рішення
Для обчислення дробу q для кожного аналіту нижньої фази ми використовуємо Equation\ ref {16.1}. Оскільки обсяги нижньої і верхньої фаз рівні, отримуємо
\[q_\text{A} = \frac {1} {D_\text{A} + 1} = \frac {1} {5 + 1} = 0.167 \quad \quad q_\text{B} = \frac {1} {D_\text{B} + 1} = \frac {1} {0.5 + 1} = 0.667 \nonumber\]
Тому що ми це знаємо\(p + q = 1 \), ми також знаємо, що p A дорівнює 0.833 і що p B дорівнює 0.333. Для аналіту А фракції в пробірках 5, 10, 15, 20, 25 і 30 після 30-ї ступені складають
\[f(5,30) = \frac {30!} {(30 - 5)! 5!} (0.833)^{5} (0.167)^{30 - 5} = 2.1 \times 10^{-15} \approx 0 \nonumber\]
\[f(10,30) = \frac {30!} {(30 - 10)! 10!} (0.833)^{10} (0.167)^{30 - 10} = 1.4 \times 10^{-9} \approx 0 \nonumber\]
\[f(15,30) = \frac {30!} {(30 - 15)! 5!} (0.833)^{15} (0.167)^{30 - 15} = 2.2 \times 10^{-5} \approx 0 \nonumber\]
\[f(20,30) = \frac {30!} {(30 - 20)! 20!} (0.833)^{20} (0.167)^{30 - 20} = 0.013 \nonumber\]
\[f(25,30) = \frac {30!} {(30 - 25)! 25!} (0.833)^{25} (0.167)^{30 - 25} = 0.192 \nonumber\]
\[f(30,30) = \frac {30!} {(30 - 30)! 30!} (0.833)^{30} (0.167)^{30 - 30} = 0.004 \nonumber\]
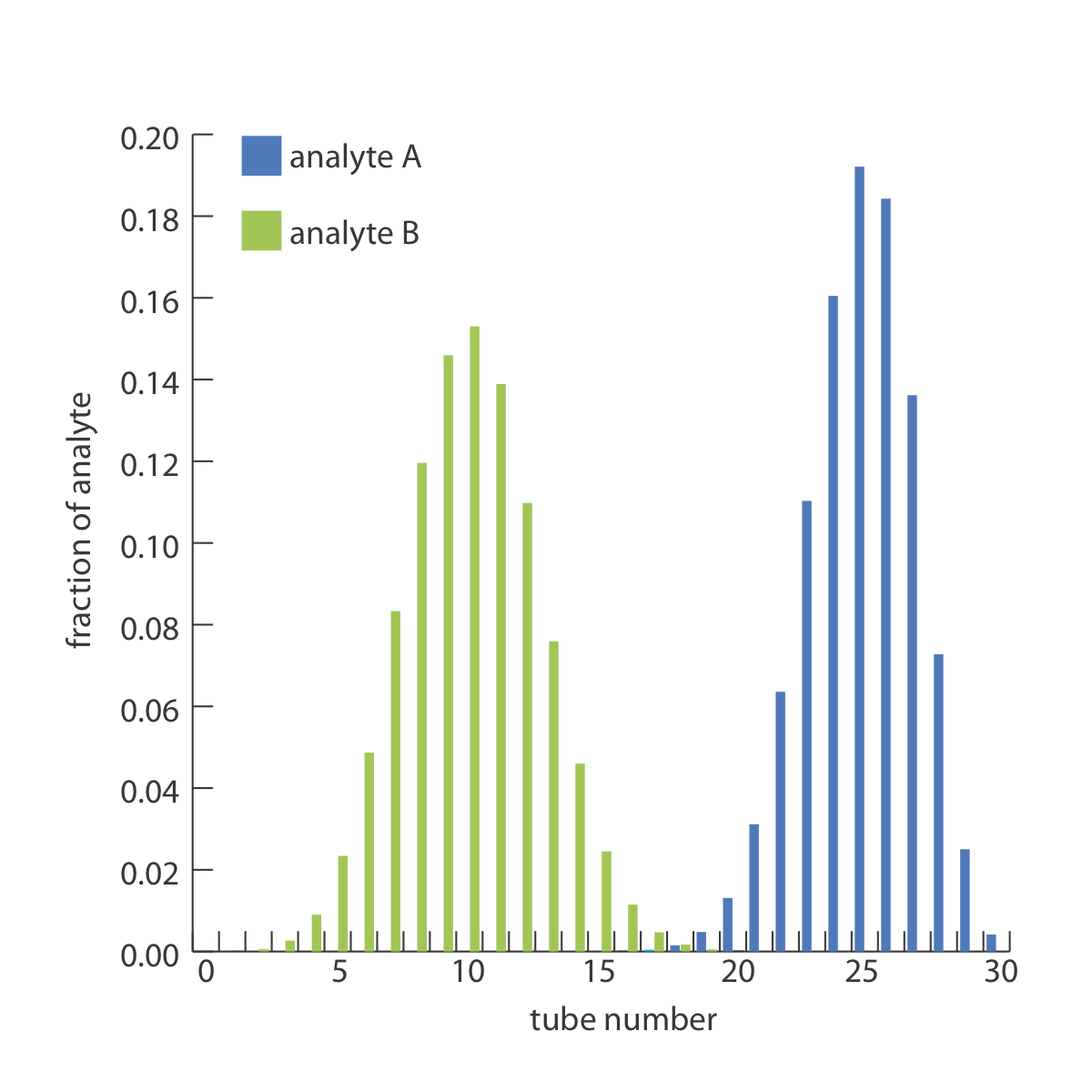
Частка аналіту В в пробірках 5, 10, 15, 20, 25 і 30 розраховується таким же чином, отримуючи відповідні значення 0,023, 0,153, 0,025, 0, 0 і 0. Рисунок Template:index, який надає повну гістограму для розподілу аналітів A і B, показує, що 30 кроків достатньо для розділення двох аналітів.
Побудова гістограми за допомогою Equation\ ref {16.2} є утомливою, особливо коли кількість кроків велика. Оскільки частка аналіту в більшості трубок дорівнює приблизно нулю, ми можемо спростити побудову гістограми, розв'язавши Equation\ ref {16.2} тільки для тих трубок, що містять кількість аналіту, що перевищує порогове значення. Для біноміального розподілу ми можемо використовувати середнє і стандартне відхилення, щоб визначити, які трубки містять значну частку аналіту. Властивості біноміального розподілу були висвітлені в главі 4 із середнім значенням\(\mu\) та стандартним відхиленням\(\sigma\), наведеним як
\[\mu = np \nonumber\]
\[\sigma = \sqrt{np(1 - p)} = \sqrt{npq} \nonumber\]
Крім того, якщо і np, і nq більше 5, то біноміальний розподіл тісно наближає нормальний розподіл, і ми можемо використовувати властивості нормального розподілу для визначення місця розташування аналіта та його відновлення [див. Mark, H.; Workman, J Spectroscopy 1990, 5 (3), 55—56].
Два аналіти, А і В, з співвідношеннями розподілу 9 і 4 відповідно, поділяються за допомогою протиточного вилучення, в якому обсяги верхньої і нижньої фаз рівні. Після 100 кроків визначають 99% довірчий інтервал для розташування кожного аналіта.
Рішення
Дріб q кожного аналіту, що залишився в нижній фазі, обчислюється за допомогою Equation\ ref {16.1}. Оскільки обсяги нижньої та верхньої фаз рівні, ми знаходимо, що
\[q_\text{A} = \frac {1} {D_\text{A} + 1} = \frac {1} {9 + 1} = 0.10 \quad \quad q_\text{B} = \frac {1} {D_\text{B} + 1} = \frac {1} {4 + 1} = 0.20 \nonumber\]
Тому що ми знаємо\(p + q = 1 \), що, ми також знаємо, що р А дорівнює 0.90 і p B 0.80. Після 100 кроків середнє і стандартне відхилення для розподілу аналітів А і В становлять
\[\mu_\text{A} = np_\text{A} = (100)(0.90) = 90 \text{ and } \sigma_\text{A} = \sqrt{np_\text{A}q_\text{A}} = \sqrt{(100)(0.90)(0.10)} = 3 \nonumber\]
\[\mu_\text{B} = np_\text{B} = (100)(0.80) = 80 \text{ and } \sigma_\text{A} = \sqrt{np_\text{A}q_\text{A}} = \sqrt{(100)(0.80)(0.20)} = 4 \nonumber\]
Враховуючи, що np A, np B, nq A і nq B все більше 5, можна припустити, що розподіл аналітів слід за нормальним розподілом і що довірчий інтервал для трубок, що містять кожну аналіт є
\[r = \mu \pm z \sigma \nonumber\]
де r - число трубки, а значення z визначається бажаним рівнем значущості. Для довірчого інтервалу 99% значення z дорівнює 2,58 (див. Додаток 4); таким чином,
\[r_\text{A} = 90 \pm (2.58)(3) = 90 \pm 8 \nonumber\]
\[r_\text{B} = 80 \pm (2.58)(4) = 80 \pm 10 \nonumber\]
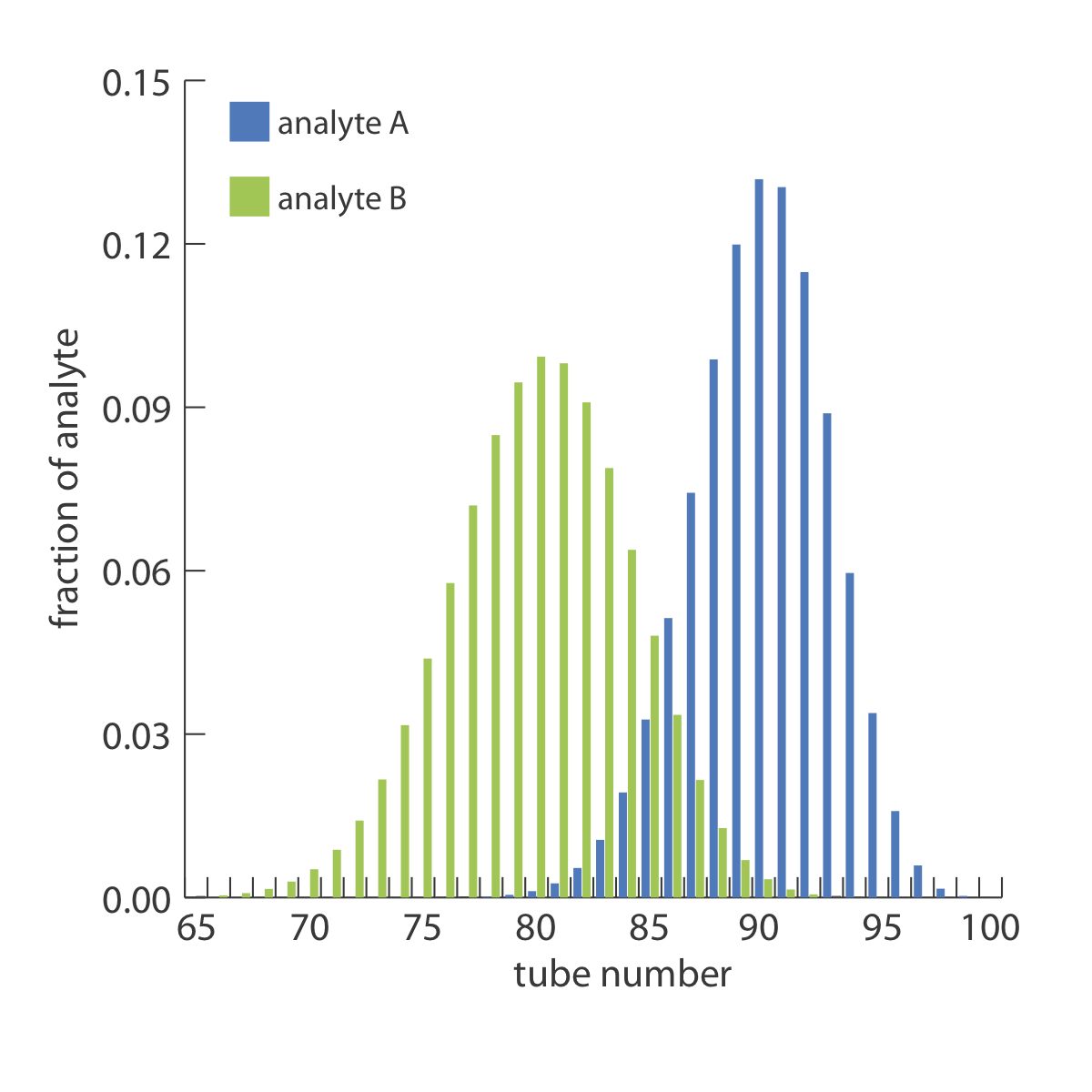
Оскільки два довірчі інтервали перекриваються, повне розділення двох аналітів неможливо за допомогою 100-ступінчастого вилучення протиструму. Повний розподіл аналітів показано на малюнку Template:index.
Для вилучення протитечії в прикладі Template:index, обчисліть відновлення та коефіцієнт поділу для аналіту А, якщо вміст трубок 85—99 об'єднано разом.
Рішення
З Прикладу Template:index ми знаємо, що після 100 кроків вилучення протиструму аналіт А зазвичай розподіляється близько трубки 90 зі стандартним відхиленням 3. Для визначення фракції аналіту А в пробірках 85—99 ми використовуємо односторонній нормальний розподіл в додатку 3 для визначення фракції аналіту в пробірках 0-84, а в трубці 100. Фракцію аналіту А в трубці 100 визначають шляхом розрахунку відхилення z
\[z = \frac {r - \mu} {\sigma} = \frac {99 - 90} {3} = 3 \nonumber\]
і використовуючи таблицю в додатку 3 для визначення відповідного дробу. Для z = 3 це відповідає 0,135% аналіту А. для визначення фракції аналіту А в трубках 0-84 знову обчислюємо відхилення.
\[z = \frac {r - \mu} {\sigma} = \frac {84 - 90} {3} = -1.67 \nonumber\]
З Додатка 3 ми знаходимо, що 4,75% аналіту А присутній в пробірках 0—84. Відновлення аналіту А, отже, є
\[100\% - 4.75\% - 0.135\% \approx 95\% \nonumber\]
Для розрахунку коефіцієнта поділу ми визначаємо відновлення аналіту В в трубках 85—99 за таким же загальним підходом, що і для аналіту А, виявивши, що приблизно 89,4% аналіту В залишається в трубках 0—84 і що по суті жоден аналіт В не знаходиться в трубці 100. Відновлення для B, отже, є
\[100\% - 89.4\% - 0\% \approx 10.6\% \nonumber\]
і коефіцієнт поділу
\[S_\text{B/A} = \frac {R_\text{A}} {R_\text{B}} = \frac {10.6} {95} = 0.112 \nonumber\]
