23.6: Кількісна потенціометрія
- Page ID
- 27189
Найважливішим застосуванням потенціометрії є визначення концентрації аналіту в розчині. Більшість потенціометричних електродів є селективними до вільної, некомплексної форми аналіту і не реагують ні на одну з складних форм аналіту. Така селективність забезпечує потенціометричним електродам значну перевагу перед іншими кількісними методами аналізу, якщо нам потрібно визначити концентрацію вільних іонів. Наприклад, кальцій присутній в сечі як у вигляді вільних іонів Ca 2+, так і у вигляді зв'язаних з білками іонів Ca 2+. Якщо ми аналізуємо зразок сечі за допомогою атомно-абсорбційної спектроскопії, сигнал є пропорційним загальній концентрації Са 2+, оскільки розпилюються як вільний, так і зв'язаний кальцій. Аналіз сечі за допомогою Ca 2+ ISE, однак, дає сигнал, який є функцією тільки вільних іонів Ca 2+, оскільки зв'язаний білком Ca 2+ не може взаємодіяти з мембраною електрода. У цьому розділі ми розглянемо кілька важливих аспектів кількісної потенціометрії.
Взаємозв'язок між концентрацією та потенціалом
У главі 23.3 ми показали, що потенціал іоноселективного електрода для іона із зарядом z дорівнює
\[E_{\mathrm{cell}}=K+\frac{0.05916}{z} \log \left(a_{A}\right)_{\mathrm{samp}} \label{quant1} \]
де K - константа, яка включає потенціали внутрішнього та зовнішнього опорних електродів іоноселективного електрода, будь-який потенціал асиметрії, пов'язаний з мембраною іоноселективного електрода, та активність аналіта у внутрішньому розчині іонселективного електрода. Рівняння\ ref {quant1} є загальним рівнянням і застосовується до всіх типів іоноселективних електродів. Зверніть увагу, що коли аналіт є катіоном, збільшення активності аналіта призводить до збільшення потенціалу; коли аналіт є аніоном, який робить z негативним числом, збільшення активності аналіта призводить до зменшення потенціалу.
Як концентрації іонів в розчині часто повідомляються у вигляді значень pX, де
\[\text{pX} = - \log a_\text{X} \label{quant2} \]
зручно підставити рівняння\ ref {quant2} в Рівняння\ ref {quant1}
\[E_{\mathrm{cell}}=K - \frac{0.05916}{z} \text{ pA} \label{quant3} \]
Зверніть увагу, що для катіону збільшення pA призводить до зменшення потенціалу; коли аналіт є аніоном, збільшення pA призводить до збільшення потенціалу.
Калібрування потенціометричних електродів
Для використання Equation\ ref {quant3} нам потрібно визначити значення K, яке ми можемо зробити за допомогою одного або декількох зовнішніх стандартів або методом стандартного додавання, обидва з яких були розглянуті в розділі 1.5. Одне ускладнення, звичайно, полягає в тому, що потенціал - це функція активності аналіта замість його концентрації.
Активність і концентрація
Рівняння\ ref {quant1} записується через активність аналіта. Однак, коли ми використовуємо потенціометричний електрод, нашою метою є визначення концентрації аналіта. Як ми дізналися в главі 22, активність іона є добутком його концентрації, [M n +] та коефіцієнта активності, залежного від матриці,\(\gamma_{Mn^{n+}}\).
\[a_{M^{n+}}=\left[M^{n+}\right] \gamma_{M^{n+}} \label{quant4} \]
Підставляючи рівняння\ ref {quant4} в рівняння\ ref {quant1} і переставляючи, дає
\[E_{\mathrm{cell}}=K+\frac{0.05916}{n} \log \gamma_{M^{n+}}+\frac{0.05916}{n} \log \left[M^{n+}\right] \label{quant5} \]
Ми можемо розв'язати Equation\ ref {quant5} для концентрації іонів металу, якщо ми знаємо значення його коефіцієнта активності. На жаль, якщо ми не знаємо точного іонного складу матриці зразка - що є звичайною ситуацією, то ми не можемо обчислити значення\(\gamma_{Mn^{n+}}\). Вирішення цієї дилеми є. Якщо ми спроектуємо нашу систему так, щоб стандарти і зразки мали однакову матрицю, то значення\(\gamma_{Mn^{n+}}\) залишається постійним і Equation\ ref {quant5} спрощує
\[E_{\mathrm{cell}}=K^{\prime}+\frac{0.05916}{n} \log \left[M^{n+}\right] \label{quanat6} \]
де\(K^{\prime}\) включає коефіцієнт активності.
Калібрування за допомогою зовнішніх стандартів
За відсутності перешкод калібрувальна крива комірки E проти журналу A, де A - аналіт, є прямою лінією. Однак графік E клітини проти журналу [A] може показувати кривизну при більш високих концентраціях аналіту в результаті матрично-залежної зміни коефіцієнта активності аналіта. Для підтримки узгодженої матриці ми додаємо високу концентрацію інертного електроліту до всіх зразків і стандартів. Якщо концентрація доданого електроліту достатня, то різниця між матрицею зразка і матрицею стандартів не вплине на іонну міцність і коефіцієнт активності по суті залишається постійним. Інертний електроліт, доданий до зразка і стандартів, називається загальним буфером регулювання іонної сили (TISAB).
Концентрацію Са 2+ в пробі води визначають за допомогою методу зовнішніх стандартів. Іонна міцність зразків і стандартів підтримується на майже постійному рівні шляхом внесення кожного розчину 0,5 М в КНО 3. Виміряні потенціали клітин для зовнішніх стандартів наведені в наступній таблиці.
| [Са 2+] (М) | E клітина (V) |
|---|---|
| \(1.00 \times 10^{-5}\) | —0,125 |
| \(5.00 \times 10^{-5}\) | —0.103 |
| \(1.00 \times 10^{-4}\) | —0,093 |
| \(5.00 \times 10^{-4}\) | —0,072 |
| \(1.00 \times 10^{-3}\) | —0,063 |
| \(5.00 \times 10^{-3}\) | —0.043 |
| \(1.00 \times 10^{-2}\) | -0.033 |
Яка концентрація Са 2+ у зразку води, якщо виявлено, що його клітинний потенціал становить —0,084 В?
Рішення
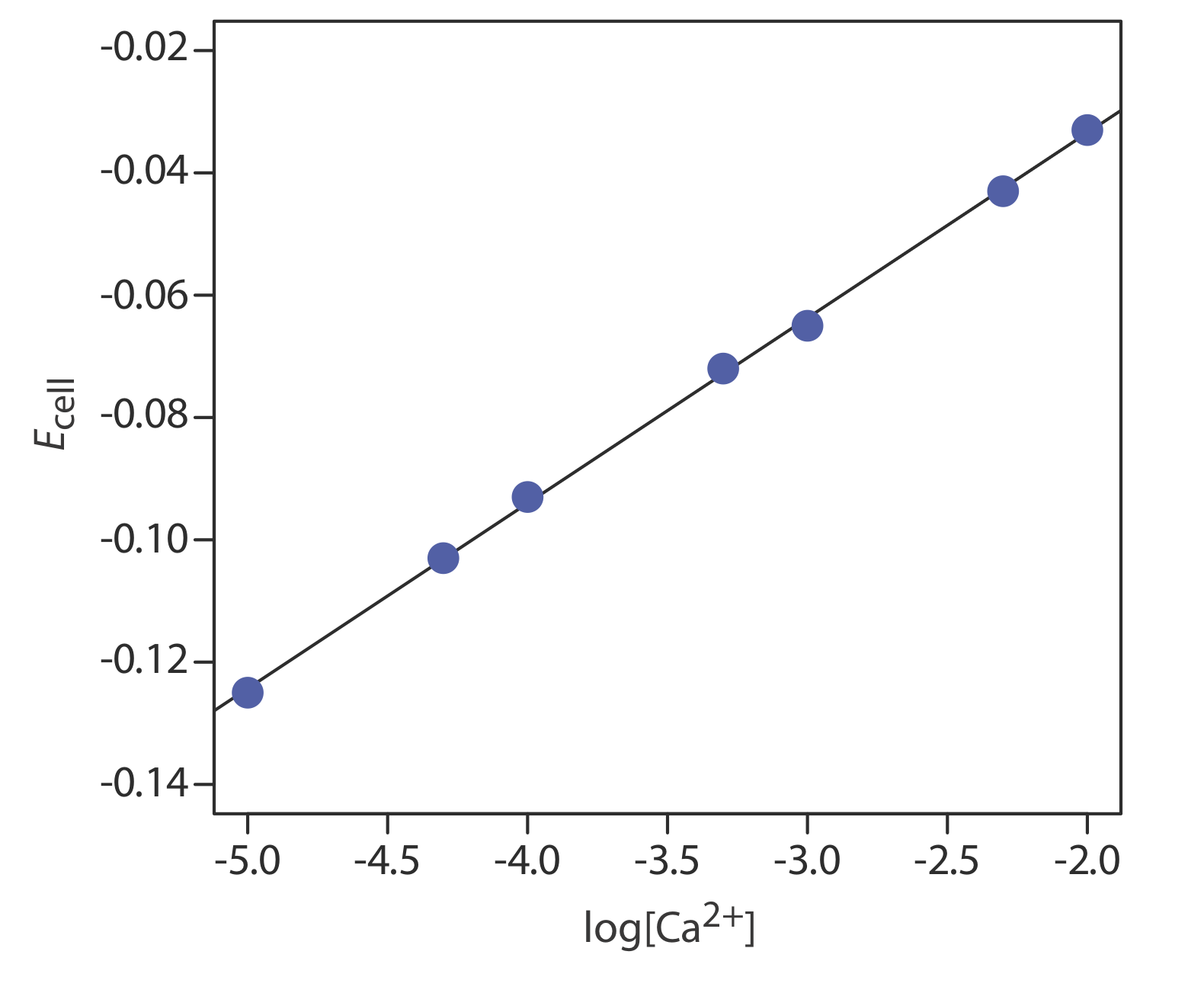
Лінійна регресія дає калібрувальну криву на малюнку\(\PageIndex{1}\), з рівнянням
\[E_{\mathrm{cell}}=0.027+0.0303 \log \left[\mathrm{Ca}^{2+}\right] \nonumber \]
Підстановка потенціалу клітини зразка дає концентрацію Са 2 + як\(2.17 \times 10^{-4}\) М. Зверніть увагу, що нахил калібрувальної кривої, який становить 0,0303, трохи більше його ідеального значення 0,05916/2 = 0,02958; це не є незвичайним і є однією з причин використання декількох стандартів. Однією з причин того, що незвично виявити, що експериментальний схил відхиляється від ідеального значення 0,05916/ п, полягає в тому, що це ідеальне значення передбачає, що температура становить 25° C.
Калібрування за допомогою стандартних доповнень
Ще одним підходом до калібрування потенціометричного електрода є метод стандартних доповнень, який був введений в главі 5.1. Спочатку переносимо пробу з об'ємом V samp і аналітичної концентрацією С samp в склянку і вимірюємо потенціал, (Е осередок) samp. Далі ми робимо стандартне додавання, додавши до зразка невеликий об'єм, V std, стандарту, який містить відому концентрацію аналіту, C std, і вимірюємо потенціал, (E клітина) std. Якщо V std значно менше V samp, то можна сміливо ігнорувати зміну матриці зразка і припустити, що коефіцієнт активності аналіта постійний. Приклад\(\PageIndex{9}\) демонструє, як ми можемо використовувати одноточкове стандартне додавання для визначення концентрації аналіту в зразку.
Концентрацію Са 2+ в пробі морської води визначають за допомогою іоноселективного електрода Са і одноточкового стандартного додавання. Пробу об'ємом 10,00 мл переносять в об'ємну колбу об'ємом 100 мл і розводять до об'єму. Аліквоту зразка об'ємом 50,00 мл поміщають у склянку з Ca ISE і опорним електродом, а потенціал вимірюють як -0,05290 В. Після додавання 1,00-мл аліквота\(5.00 \times 10^{-2}\) M стандартного розчину Ca 2 + потенціал становить —0,04417 В. Яка концентрація Са 2 + в пробі морської води?
Рішення
Для початку запишемо рівняння Нернста до і після додавання стандартного додавання. Потенціал клітини для зразка
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{samp}}=K+\frac{0.05916}{2} \log C_{\mathrm{samp}} \nonumber \]
і що після стандартного доповнення
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{std}}=K+\frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} \nonumber \]
де V tot - загальний обсяг (V samp + V std) після стандартного додавання. Віднімання першого рівняння з другого рівняння дає
\[\Delta E = \left(E_{\mathrm{cell}}\right)_{\mathrm{std}} - \left(E_{\mathrm{cell}}\right)_{\mathrm{samp}} = \frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} - \frac{0.05916}{2}\log C_\text{samp} \nonumber \]
Перестановка цього рівняння залишає нас
\[\frac{2 \Delta E_{cell}}{0.05916} = \log \left\{ \frac {V_\text{samp}} {V_\text{tot}} + \frac {V_\text{std}C_\text{std}} {V_\text{tot}C_\text{samp}} \right\} \nonumber \]
Підставляючи відомі значення для\(\Delta E\), V samp, V std, V tot і C std,
\[\begin{array}{l}{\frac{2 \times\{-0.04417-(-0.05290)\}}{0.05916}=} \\ {\log \left\{\frac{50.00 \text{ mL}}{51.00 \text{ mL}}+\frac{(1.00 \text{ mL})\left(5.00 \times 10^{-2} \mathrm{M}\right)}{(51.00 \text{ mL}) C_{\mathrm{samp}}}\right\}} \\ {0.2951=\log \left\{0.9804+\frac{9.804 \times 10^{-4}}{C_{\mathrm{samp}}}\right\}}\end{array} \nonumber \]
і взяття зворотного журналу обох сторін дає
\[1.973=0.9804+\frac{9.804 \times 10^{-4}}{C_{\text {samp }}} \nonumber \]
Нарешті, рішення для C samp дає концентрацію Са 2 + як\(9.88 \times 10^{-4}\) М. Оскільки ми розбавили вихідну пробу морської води в 10 разів, концентрація Са 2 + в зразку морської води становить\(9.88 \times 10^{-3}\) M.
Оперативне визначення рН
При наявності недорогих скляних рН-електродів і рН-метрів визначення рН є одним з найбільш поширених кількісних аналітичних вимірювань. Потенціометричне визначення рН, однак, не позбавлене ускладнень, деякі з яких ми обговоримо в цьому розділі.
Одним з ускладнень є плутанина щодо значення рН [Крістенсен, Х.Б.; Саломан, А.; Kokholm, G Anal. Хім. 1991, 63, 885—891А]. Умовне визначення рН в більшості загальних підручників з хімії дано з точки зору концентрації Н +
\[\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right] \label{quant7} \]
Як ми тепер знаємо, коли ми вимірюємо рН, це насправді є мірою активності Н +.
\[\mathrm{pH}=-\log a_{\mathrm{H}^{+}} \label{quant8} \]
Спробуйте цей експеримент - знайдіть кілька загальних підручників з хімії та знайдіть рН в індексі кожного підручника. Зверніться до відповідних сторінок і подивіться, як це визначено. Далі перегляньте коефіцієнт активності або активності в індексі кожного підручника та перевірте, чи індексуються ці терміни.
Рівняння\ ref {quant7} лише наближає істинний рН. Якщо обчислити рН 0,1 М HCl за допомогою рівняння\ ref {quant7}, то отримаємо значення 1,00; фактичний рН розчину, як визначено Equation\ ref {quant8}, становить 1,1 [Hawkes, SJ J. Chem. Едук. 1994, 71, 747—749]. Активність і концентрація Н + не однакові в 0,1 М HCl, оскільки коефіцієнт активності для Н + не дорівнює 1,00 в цій матриці. \(\PageIndex{2}\)На малюнку показана більш барвиста демонстрація різниці між активністю і концентрацією.

Другим ускладненням при вимірюванні рН є невизначеність у взаємозв'язку між потенціалом і активністю. Для електрода скляної мембрани потенціал клітини, (E клітина) samp, для зразка з невідомим рН становить
\[(E_{\text{cell}})_\text {samp} = K-\frac{R T}{F} \ln \frac{1}{a_{\mathrm{H}^{+}}}=K-\frac{2.303 R T}{F} \mathrm{pH}_{\mathrm{samp}} \label{quant9} \]
де К включає потенціал опорного електрода, потенціал асиметрії скляної мембрани і будь-які потенціали переходу в електрохімічній комірці. Всі внески до К схильні до невизначеності, і можуть змінюватися з кожним днем, а також від електрода до електрода. З цієї причини перед використанням pH-електрода ми калібруємо його за допомогою стандартного буфера відомого рН. Потенціал клітини для стандартної, (E клітини) std, є
\[\left(E_{\text {ccll}}\right)_{\text {std}}=K-\frac{2.303 R T}{F} \mathrm{p} \mathrm{H}_{\mathrm{std}} \label{quant10} \]
де pH std є стандартним рН. Віднімання рівняння\ ref {quan10} з рівняння\ ref {quant9} і розв'язування для pH samp дає
\[\text{pH}_\text{samp} = \text{pH}_\text{std} - \frac{\left\{\left(E_{\text {cell}}\right)_{\text {samp}}-\left(E_{\text {cell}}\right)_{\text {std}}\right\} F}{2.303 R T} \label{quant11} \]
яке є оперативним визначенням рН, прийнятим Міжнародним союзом чистої та прикладної хімії [Ковінгтон, А.К.; Бейтс, Р.Б.; Durst, R.A. Pure & Appl. Хім. 1985, 57, 531—542].
Калібрування електрода pH представляє третє ускладнення, оскільки нам потрібен стандарт з точно відомою активністю для H +. Таблиця\(\PageIndex{1}\) містить значення рН для декількох первинних стандартних буферних розчинів, прийнятих Національним інститутом стандартів і технологій.
Щоб стандартизувати електрод pH за допомогою двох буферів, виберіть один поблизу рН 7 і один, який є більш кислим або основним, залежно від очікуваного рН вашого зразка. Промийте електрод pH в деіонізованій воді, промокніть його насухо лабораторною серветкою і помістіть його в буфер з рН, найближчим до 7. Закрутіть pH-електрод і дайте йому врівноважитися, поки не отримаєте стабільне показання. Відрегулюйте ручку «Стандартизувати» або «Калібрувати», поки лічильник не відобразить правильний рН. Промийте і висушіть електрод, а також помістіть його в другий буфер. Після того, як електрод вирівняється, відрегулюйте регулятор «Нахил» або «Температура», поки лічильник не покаже правильний рН.
Деякі рН-метри можуть компенсувати зміну температури. Щоб скористатися цією функцією, помістіть в зразок температурний зонд і підключіть його до рН-метра. Налаштуйте регулятор «Температура» відповідно до температури розчину та відкалібруйте рН-метр за допомогою елементів керування «Калібрувати» та «Нахил». Коли ви використовуєте електрод рН, рН-метр компенсує будь-яку зміну температури зразка, регулюючи нахил калібрувальної кривої за допомогою реакції Нернстіана 2,303 RT/F.
