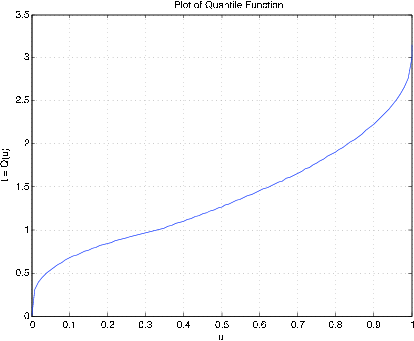
10.3: Функція квантиля
- Page ID
- 98491
Функція квантилі
Квантильна функція для розподілу ймовірностей має багато застосувань як у теорії, так і в застосуванні ймовірності. Якщо\(F\) є функцією розподілу ймовірностей, квантильна функція може бути\(F\) використана для «побудови» випадкової величини, яка має функцію розподілу. Цей факт служить основою методу моделювання «вибірки» з довільного розподілу за допомогою генератора випадкових чисел. Крім того, враховуючи будь-який кінцевий клас
\(\{X_i: 1 \le i \le n\}\)випадкових величин\(\{Y_i: 1 \le i \le n\}\) може бути побудовано незалежний клас,\(X_i\) причому кожен з них\(Y_i\) має однаковий (граничний) розподіл. Квантильні функції для простих випадкових величин можуть бути використані для отримання важливої теореми про наближення Пуассона (яку ми не розробляємо в цій роботі). Квантильна функція використовується для отримання ряду корисних спеціальних форм для математичного очікування.
Загальне поняття — властивості та приклади
Якщо\(F\) є функцією розподілу ймовірностей, то асоційована\(Q\) квантильна функція по суті є оберненою\(F\). Квантильна функція визначається на одиничному інтервалі (0, 1). Для\(F\) безперервного і строго збільшення в\(t\), потім\(Q(u) = t\) iff\(F(t) = u\). Таким чином, якщо\(u\) є значенням ймовірності,\(t = Q(u)\) це значення\(t\) для якого\(P(X \le t) = u\).
Приклад 10.3.28: Розподіл Вейбулла (3, 2, 0)
\(u = F(t) = 1 - e^{-3t^2}\)\(t \ge 0\)\(\Rightarrow\)\(t = Q(u) = \sqrt{-\text{ln } (1 - u)/3}\)
Приклад 10.3.29: Нормальний розподіл
M-функція norminv, заснована на MATLAB функції erfinv (обернена функція похибки), обчислює значення\(Q\) нормального розподілу.
Обмеження безперервного випадку не є суттєвим. Розглянуто загальне визначення, яке застосовується до будь-якої функції розподілу ймовірностей.
Означення: Якщо\(F\) функція має властивості функції розподілу ймовірностей, то квантильна функція для\(F\) задається
\(Q(u) = \text{inf } \{t: F(t) \ge u\}\)\(\forall u \in (0, 1)\)
Відзначимо
- Якщо\(F(t^{*}) \ge u^{*}\), то\(t^{*} \ge \text{inf } \{t: F(t) \ge u^{*}\} = Q(u^{*})\)
- Якщо\(F(t^{*}) < u^{*}\), то\(t^{*} < \text{inf } \{t: F(t) \ge u^{*}\} = Q(u^{*})\)
Значить, у нас є важлива властивість:
(Q1)\(Q(u) \le t\) вимкнено\(u \le F(t)\)\(\forall u \in (0, 1)\)
Майно (Q1) має на увазі наступне важливе властивість:
(Q2) Якщо\(U\) ~ рівномірний (0, 1), то\(X = Q(U)\) має функцію розподілу\(F_X = F\). Щоб переконатися в цьому, зверніть увагу, що\(F_X(t) = P(Q(U) \le t] = P[U \le F(t)] = F(t)\).
Властивість (Q2) має на увазі,\(F\) що якщо будь-яка функція розподілу, з квантильної функцією\(Q\), то випадкова величина\(X = Q(U)\), з\(U\) рівномірно розподіленим по (0, 1), має функцію розподілу\(F\).
Приклад 10.3.30: Незалежні класи з прописаними розподілами
Припустимо,\(\{X_i: 1 \le i \le n\}\) це довільний клас випадкових величин з відповідними функціями розподілу\(\{F_i : 1 \le i \le n\}\). \(\{Q_i: 1 \le i \le n\}\)Дозволяти відповідні квантильні функції. Завжди існує незалежний клас\(\{U_i: 1 \le i \le n\}\) iid uniform (0, 1) (маргінали для спільного рівномірного розподілу на одиничному гіперкубі зі сторонами (0, 1)). Потім випадкові величини\(Y_i = Q_i (U_i)\)\(1 \le i \le n\) утворюють незалежний клас з тими ж маргіналами, що і\(X_i\).
Може бути встановлено кілька інших важливих властивостей квантильної функції.
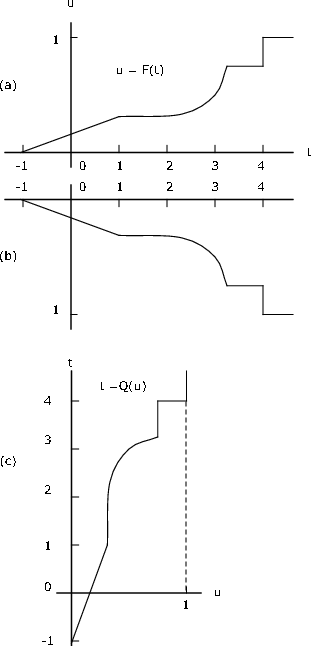
\(Q\)ліворуч безперервний, тоді як\(F\) право-безперервний.
Якщо стрибки представлені вертикальними відрізками лінії, побудова графіка\(u = Q(t)\) може бути отримана наступною двоетапною процедурою:
- Інвертувати всю фігуру (включаючи осі), потім
- Поверніть отриману цифру на 90 градусів проти годинникової стрілки
Це проілюстровано на малюнку 10.3.9. Якщо стрибки представлені вертикальними відрізками лінії, то стрибки йдуть в плоскі відрізки, а плоскі відрізки переходять у вертикальні відрізки.
Якщо\(X\) дискретний з ймовірністю\(p_i\) при\(t_i\)\(1 \le i \le n\), то\(F\) має скачки суми\(p_i\) на кожному\(t_i\) і постійний між ними. Квантильна функція - це ліво-безперервна крокова функція, що має значення\(t_i\) на інтервалі\((b_{i - 1}, b_i]\), де\(b_0 = 0\) і\(b_i = \sum_{j = 1}^{i} p_j\). Про це можна констатувати
Якщо\(F(t_i) = b_i\), то\(Q(u) = t_i\) для\(F(t_{i - 1}) < u \le F(t_i)\)
Приклад 10.2.31: Квантильна функція для простої випадкової величини
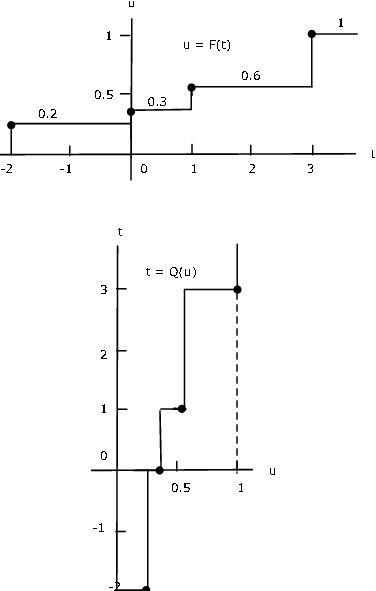
Припустимо, проста випадкова величина\(X\) має розподіл
\(X =\)[-2 0 1 3]\ (ПІКС = 0.2 0.1 0,3 0,4]
На малюнку 1 показаний графік функції розподілу\(F_X\). Він відбивається на горизонтальній осі, потім обертається проти годинникової стрілки, щоб дати графік\(Q(u\) проти\(u\).
Використано наведену вище аналітичну характеристику при розробці ряду m-функцій та m-процедур.
m-процедури для простої випадкової величини
Основою розрахунків квантильної функції для простої випадкової величини є формула вище. Це реалізовано в m-функції dquant, яка використовується як елемент декількох процедур моделювання. Для побудови квантильної функції ми використовуємо dquanplot, який використовує функцію сходів та графіки\(X\) проти функції розподілу\(FX\). Процедура вибірки використовує квант для отримання «вибірки» з сукупності з простим розподілом і для обчислення відносних частот різних значень.
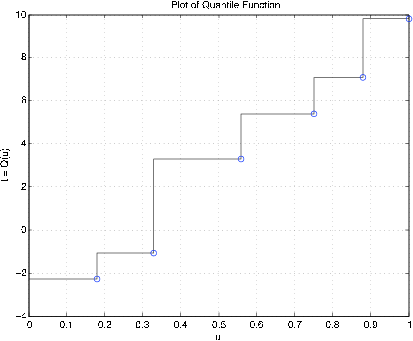
Приклад 10.3.32: Проста випадкова величина
X = [-2.3 -1.1 3.3 5.4 7.1 9.8];
PX = 0.01*[18 15 23 19 13 12];
dquanplot
Enter VALUES for X X
Enter PROBABILITIES for X PX % See Figure 10.3.11 for plot of results
rand('seed',0) % Reset random number generator for reference
dsample
Enter row matrix of values X
Enter row matrix of probabilities PX
Sample size n 10000
Value Prob Rel freq
-2.3000 0.1800 0.1805
-1.1000 0.1500 0.1466
3.3000 0.2300 0.2320
5.4000 0.1900 0.1875
7.1000 0.1300 0.1333
9.8000 0.1200 0.1201
Sample average ex = 3.325
Population mean E[X] = 3.305
Sample variance = 16.32
Population variance Var[X] = 16.33
Іноді бажано знати, скільки випробувань потрібно для досягнення певної величини, або одного з набору значень. Пара m-процедур доступні для моделювання цієї проблеми. Перший називається targetset. Він вимагає розподілу населення, а потім позначення «цільового набору» можливих значень. Друга процедура, targetrun, вимагає кількість повторень експерименту і запитує кількість членів цільового набору, яке потрібно досягти. Після того, як прогони зроблені, розраховується і виводиться різна статистика по трасах.
X = [-1.3 0.2 3.7 5.5 7.3]; % Population values PX = [0.2 0.1 0.3 0.3 0.1]; % Population probabilities E = [-1.3 3.7]; % Set of target states targetset Enter population VALUES X Enter population PROBABILITIES PX The set of population values is -1.3000 0.2000 3.7000 5.5000 7.3000 Enter the set of target values E Call for targetrun
rand('seed',0) % Seed set for possible comparison
targetrun
Enter the number of repetitions 1000
The target set is
-1.3000 3.7000
Enter the number of target values to visit 2
The average completion time is 6.32
The standard deviation is 4.089
The minimum completion time is 2
The maximum completion time is 30
To view a detailed count, call for D.
The first column shows the various completion times;
the second column shows the numbers of trials yielding those times
% Figure 10.6.4 shows the fraction of runs requiring t steps or less
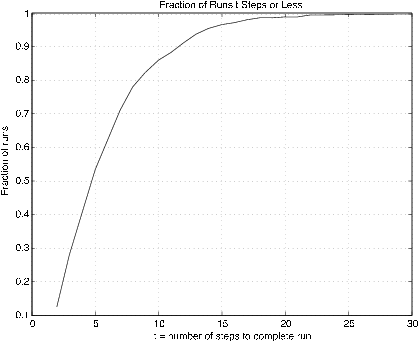
m-процедури для функцій розподілу
Процедура dfsetup використовує функцію розподілу, щоб налаштувати приблизний простий розподіл. Кванплот m-процедури використовується для побудови квантильної функції. Ця процедура, по суті, така ж, як dquanplot, за винятком звичайної функції графіка використовується в неперервному випадку, тоді як функція побудови сходів використовується в дискретному випадку. Для отримання вибірки з популяції використовується m-процедурна вибірка. Оскільки існує так багато можливих значень, вони не відображаються, як у дискретному випадку.
Приклад 10.3.34: Квантильна функція, пов'язана з функцією розподілу
F = '0.4*(t + 1).*(t < 0) + (0.6 + 0.4*t).*(t >= 0)'; % String dfsetup Distribution function F is entered as a string variable, either defined previously or upon call Enter matrix [a b] of X-range endpoints [-1 1] Enter number of X approximation points 1000 Enter distribution function F as function of t F Distribution is in row matrices X and PX quanplot Enter row matrix of values X Enter row matrix of probabilities PX Probability increment h 0.01 % See Figure 10.3.13 for plot qsample Enter row matrix of X values X Enter row matrix of X probabilities PX Sample size n 1000 Sample average ex = -0.004146 Approximate population mean E(X) = -0.0004002 % Theoretical = 0 Sample variance vx = 0.25 Approximate population variance V(X) = 0.2664
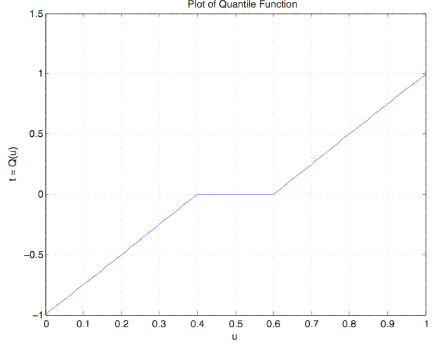
m-процедури для функцій щільності
Для отримання простого приблизного розподілу використовується m- процедура acsetup. Це по суті те ж саме, що і процедура tuappr, за винятком того, що функція щільності вводиться як строкова змінна. Потім використовуються процедури quanplot і qsample, як у випадку функцій розподілу.
Приклад 10.3.35: Квантильна функція, пов'язана з функцією щільності
acsetup
Density f is entered as a string variable.
either defined previously or upon call.
Enter matrix [a b] of x-range endpoints [0 3]
Enter number of x approximation points 1000
Enter density as a function of t '(t.^2).*(t<1) + (1- t/3).*(1<=t)'
Distribution is in row matrices X and PX
quanplot
Enter row matrix of values X
Enter row matrix of probabilities PX
Probability increment h 0.01 % See Figure 10.3.14 for plot
rand('seed',0)
qsample
Enter row matrix of values X
Enter row matrix of probabilities PX
Sample size n 1000
Sample average ex = 1.352
Approximate population mean E(X) = 1.361 % Theoretical = 49/36 = 1.3622
Sample variance vx = 0.3242
Approximate population variance V(X) = 0.3474 % Theoretical = 0.3474