6.3: Статистика перелому
- Page ID
- 30672
Вступ
Одним з особливо клопітких аспектів руйнування, особливо в високоміцних і крихких матеріалах, є його мінливість. Проектувальник повинен вміти справлятися з цим, і обмежувати навантаження тими, які знижують ймовірність відмови до прийнятно низького рівня. Вибір прийнятного рівня ризику - це складне дизайнерське рішення, очевидно, максимально наближене до нуля у випадках, коли безпека людини задіяна, але вище в дверних ручках та інших недорогих предметах, де відмова не надто більше, ніж неприємність. Наступні розділи не замінять ретельного вивчення статистики, але введуть принаймні деякі основні аспекти статистичної теорії, необхідні при проектуванні проти руйнування. Текст Коллінза (Collins, JA, Failure of Materials in Mechanical Design, Wiley, 1993.) включає розширену обробку статистичного аналізу даних про руйнування та втоми, і рекомендується для подальшого читання.
Основні статистичні заходи
Значення міцності на розрив,\(\sigma_f\) наведене в довідниках з властивостей матеріалів, зазвичай є середнім арифметичним, просто сумою ряду індивідуальних вимірювань міцності, поділеної на кількість випробуваних зразків:
\[\overline{\sigma_f} = \dfrac{1}{N} \sum_{i = 1}^{N} \sigma_{f,i}\]
де оверлайн позначає середнє значення і\(\sigma_f, i\) є виміряною силою\(i^{th}\) (поза\(N\)) окремого зразка. Звичайно, не всі екземпляри мають сильні сторони точно рівні середньому; деякі слабкіші, деякі сильніші. Існує кілька заходів того, наскільки широко розсіяним є розподіл сильних сторін, одним з важливих є вибірка стандартного відхилення, свого роду середньоквадратичне середнє значення окремих відхилень від середнього:
\[s = \sqrt{\dfrac{1}{N-1} \sum_{i = 1}^{N} (\overline{\sigma_f} - \sigma_{x,i})^2}\]
Значення\(s\) для дизайнера, як правило, щодо того, наскільки великий він порівнюється із середнім, тому зазвичай використовується коефіцієнт варіації, або CV:
\(\text{C.V.} = \dfrac{s}{\overline{\sigma_f}}\)
Це часто виражається у відсотках. Коефіцієнти варіації міцності на розрив зазвичай знаходяться в діапазоні 1— 10%, причому значення набагато більше, що вказують на істотну невідповідність при підготовці зразка або експериментальну помилку.
Приклад\(\PageIndex{1}\)
Для ілюстрації статистичних методів, які будуть викладені в цьому Модулі, ми використаємо послідовність із тридцяти вимірювань міцності на розрив при кімнатній температурі графітово-епоксидного композиту (П.Шиприкевич, ASTM STP 1003, pp. 111—135, 1989.). Цими даними (у кпсі) є: 72,5, 73.8, 68.1, 77.9, 65.5, 73.23, 71.17, 79.92, 65.67, 74.28, 67.95, 82.84, 79.83, 80.52, 70.65, 72.85, 77.81, 72.29, 75.78, 67.03, 72.85, 77.81, 75.81 33, 71.75, 72.28, 79.08, 71.04, 67.84, 69.2, 71.53. Ще тридцять вимірювань з того ж джерела, але знятих при 93\(^{\circ} C\) і -59\(^{\circ} C\), наведені в проб. 2 і 3, і можуть бути піддані тим же обробкам, що і домашнє завдання.
Існує кілька комп'ютерних пакетів, доступних для проведення статистичних розрахунків, і більшість процедур, які будуть викладені тут, можуть бути виконані за допомогою електронних таблиць. Функціями Microsoft Excel для середнього та стандартного відхилення є середнє () та stdev (), де аргументами є діапазон комірок, що містять дані. Вони дають для вищевказаних даних
\(\overline{\sigma_f} = 73.28, \ \ \ s = 4.63 \text{ (kpsi)}\)
Коефіцієнт варіації дорівнює\(\text{C.V.} = (4.63/73.28) \times 100% = 6.32%\).
Нормальний розподіл
Більш повна картина мінливості сили виходить, якщо на гістограмі побудовано число окремих сильних сторін зразка,\(\Delta \sigma_f\) що падають в дискретному інтервалі міцності, проти σ f на гістограмі, як показано на малюнку 1; максимум в гістограмі буде близько середньої сили, а його ширина буде пов'язана з стандартне відхилення.
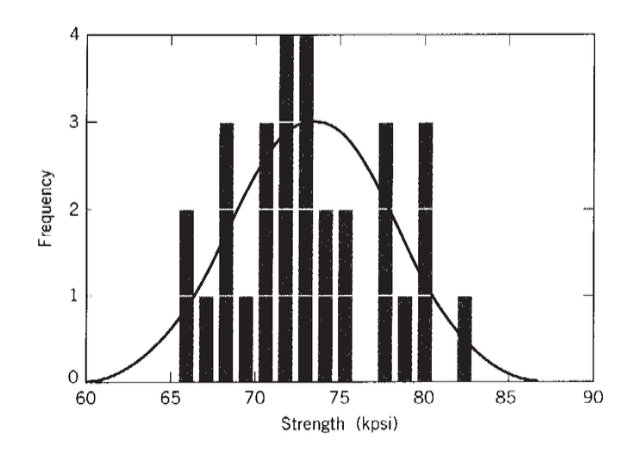
Зі збільшенням кількості зразків гістограму можна малювати з більш тонкими\(\Delta \sigma_f\) кроками, в кінцевому підсумку утворюючи плавну функцію розподілу ймовірностей або «pdf». Математична форма цієї функції залежить від матеріалу (а також методу випробувань в деяких випадках), щоб вирішити, але багато явищ в природі можуть бути описані задовільно нормальною, або Гауссовой, функцією:
\[f(X) = \dfrac{1}{\sqrt{2\pi}} \exp \dfrac{-X^2}{2}, \ \ \ X = \dfrac{\sigma_f - \overline{\sigma_f}}{s}\]
Ось\(X\) стандартна нормальна змінна, і просто скільки стандартних відхилень окремого зразка міцності знаходиться далеко від середнього. Фактор\(1/\sqrt{2 \pi}\) нормалізує функцію так, що її інтегралом є єдність, яка необхідна, якщо зразок повинен мати 100% ймовірність невдачі при певному стресі. У цьому виразі ми припустили, що міра стандартного відхилення, визначеного з Рівняння 6.3.2 на основі дискретної кількості зразків, прийнятно близька до «істинного» значення, яке було б отримано, якби кожен шматок матеріалу у Всесвіті міг би якось бути випробуваний.
Функція нормального розподілу\(f(X)\) виглядає як «крива дзвінка», знайома всім учням, що свідомі класу. Його інтеграл, відомий як функція кумулятивного розподілу або\(P_f(X)\), також використовується зазвичай; його ордината - це ймовірність руйнування, а також фракція зразків, що мають міцність нижче, ніж пов'язане з цим абссісальне значення. Оскільки нормальний pdf був нормалізований, кумулятивна функція піднімається з S-подібною або сигмоїдальною формою, щоб наблизитися до єдності при великих значеннях\(X\). Дві функції\(f(X)\) і\(F(X)\) побудовані на малюнку 2, і наведені в таблицях 1 і 2 Додатка, що додаються до цього модуля. (Часто також\(P_s = 1−P_f\) використовується ймовірність виживання; ця крива починається майже з одиниці і падає в сигмоїдальній формі до нуля зі збільшенням прикладеного напруження.)
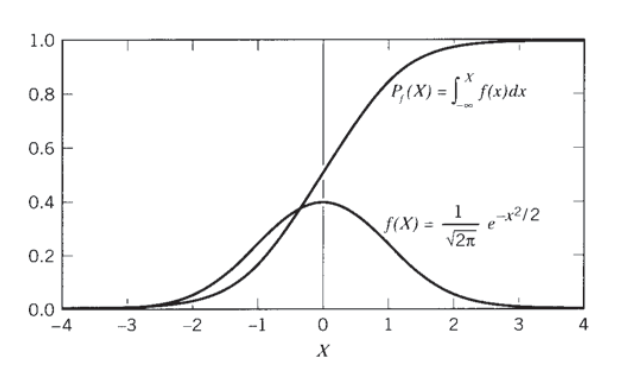
Малюнок 2: Диференціальні\(f(X)\) та кумулятивні\(P_f(X)\) нормальні ймовірнісні функції.
Одним із зручних засобів визначення того, чи нормально розподіляється конкретний набір вимірювань, є використання спеціального графічного паперу (копія включена в Додаток), ордината якого була спотворена, щоб зробити сигмоїдальний графік кумулятивного розподілу Pf як пряму лінію. (Іноді легше працювати з прямими лініями на пишному папері, ніж пишними лініями на прямому папері.) Експериментальні дані ранжуються від найнижчого до найвищого, і кожному присвоюється ранг на основі частки сильних сторін, що мають більш високі значення. Якщо ранги присвоюються як i/ (N + 1), де i - позиція бази в упорядкованому списку, а N - кількість зразків, ряди завжди більші за нуль і менше одиниці; це полегшує складання графіків.
Ступінь, до якої ці дані про силу рангу відображаються як прямі лінії на папері нормальної ймовірності, є візуальною мірою того, наскільки добре дані описуються нормальним розподілом. Найкраща пряма лінія через точки проходить 50% кумулятивну лінію фракції на середньому вибірці, а її нахил дає стандартний розподіл. Побудова декількох з цих ліній, наприклад, для різних умов обробки даного матеріалу, є зручним способом охарактеризувати різниці міцності, що виникають з двох умов (див. Приб. 2).
Приклад\(\PageIndex{2}\)
Для нашої тестової популяції тридцяти зразків упорядковані та ранжовані дані:
| \(i\) | \(\sigma_{f,i}\) | \(P_f = \dfrac{i}{N+1}\) |
|---|---|---|
| \ (i\) ">1 | \ (\ сигма_ {f, i}\) ">65.50 | \ (p_f =\ dfrac {i} {N+1}\) ">0.0323 |
| \ (i\) ">2 | \ (\ сигма_ {f, i}\) ">65.67 | \ (p_f =\ dfrac {i} {N+1}\) ">0.0645 |
| \ (i\) ">3 | \ (\ сигма_ {f, i}\) ">67.03 | \ (p_f =\ dfrac {i} {N+1}\) ">0.0968 |
| \ (i\) ">4 | \ (\ сигма_ {f, i}\) ">67.84 | \ (p_f =\ dfrac {i} {N+1}\) ">0.1290 |
| \ (i\) ">5 | \ (\ сигма_ {f, i}\) ">67,95 | \ (p_f =\ dfrac {i} {N+1}\) ">0.1613 |
| \ (i\) ">6 | \ (\ сигма_ {f, i}\) ">68.10 | \ (p_f =\ dfrac {i} {N+1}\) ">0.1935 |
| \ (i\) ">7 | \ (\ сигма_ {f, i}\) ">69.20 | \ (p_f =\ dfrac {i} {N+1}\) ">0.2258 |
| \ (i\) ">8 | \ (\ сигма_ {f, i}\) ">70.65 | \ (p_f =\ dfrac {i} {N+1}\) ">0.2581 |
| \ (i\) ">9 | \ (\ сигма_ {f, i}\) ">71.04 | \ (p_f =\ dfrac {i} {N+1}\) ">0.2903 |
| \ (i\) ">10 | \ (\ сигма_ {f, i}\) ">71.17 | \ (p_f =\ dfrac {i} {N+1}\) ">0.3226 |
| \ (i\) ">11 | \ (\ сигма_ {f, i}\) ">71.53 | \ (p_f =\ dfrac {i} {N+1}\) ">0.3548 |
| \ (i\) ">12 | \ (\ сигма_ {f, i}\) ">71.75 | \ (p_f =\ dfrac {i} {N+1}\) ">0.3871 |
| \ (i\) ">13 | \ (\ сигма_ {f, i}\) ">72.28 | \ (p_f =\ dfrac {i} {N+1}\) ">0.4194 |
| \ (i\) ">14 | \ (\ сигма_ {f, i}\) ">72.29 | \ (p_f =\ dfrac {i} {N+1}\) ">0.4516 |
| \ (i\) ">15 | \ (\ сигма_ {f, i}\) ">72.5 | \ (p_f =\ dfrac {i} {N+1}\) ">0.4839 |
| \ (i\) ">16 | \ (\ сигма_ {f, i}\) ">72.85 | \ (p_f =\ dfrac {i} {N+1}\) ">0.5161 |
| \ (i\) ">17 | \ (\ сигма_ {f, i}\) ">72.85 | \ (p_f =\ dfrac {i} {N+1}\) ">0.5484 |
| \ (i\) ">18 | \ (\ сигма_ {f, i}\) ">72.23 | \ (p_f =\ dfrac {i} {N+1}\) ">0.5806 |
| \ (i\) ">19 | \ (\ сигма_ {f, i}\) ">73.80 | \ (p_f =\ dfrac {i} {N+1}\) ">0.6129 |
| \ (i\) ">20 | \ (\ сигма_ {f, i}\) ">74.28 | \ (p_f =\ dfrac {i} {N+1}\) ">0.6452 |
| \ (i\) ">21 | \ (\ сигма_ {f, i}\) ">75.33 | \ (p_f =\ dfrac {i} {N+1}\) ">0.6774 |
| \ (i\) ">22 | \ (\ сигма_ {f, i}\) ">75.78 | \ (p_f =\ dfrac {i} {N+1}\) ">0.7097 |
| \ (i\) ">23 | \ (\ сигма_ {f, i}\) ">77.81 | \ (p_f =\ dfrac {i} {N+1}\) ">0.7419 |
| \ (i\) ">24 | \ (\ сигма_ {f, i}\) ">77.81 | \ (p_f =\ dfrac {i} {N+1}\) ">0.7742 |
| \ (i\) ">25 | \ (\ сигма_ {f, i}\) ">77.90 | \ (p_f =\ dfrac {i} {N+1}\) ">0.8065 |
| \ (i\) ">26 | \ (\ сигма_ {f, i}\) ">79.08 | \ (p_f =\ dfrac {i} {N+1}\) ">0.8387 |
| \ (i\) ">27 | \ (\ сигма_ {f, i}\) ">79.83 | \ (p_f =\ dfrac {i} {N+1}\) ">0.8710 |
| \ (i\) ">28 | \ (\ сигма_ {f, i}\) ">79.92 | \ (p_f =\ dfrac {i} {N+1}\) ">0.9032 |
| \ (i\) ">29 | \ (\ сигма_ {f, i}\) ">80.52 | \ (p_f =\ dfrac {i} {N+1}\) ">0.9355 |
| \ (i\) ">30 | \ (\ сигма_ {f, i}\) ">82.84 | \ (p_f =\ dfrac {i} {N+1}\) ">0.9677 |
Коли вони побудовані за допомогою масштабування ймовірності на ординаті, виходить графік на малюнку 3.
Нормальна функція розподілу була охарактеризована ретельно, і з неї можна зробити висновок про розподіли сили, близькі до нормальних. Наприклад, сукупна функція нормального розподілу (cdf), таблична в таблиці 2 Додатка, показує, що 68,3% всіх членів нормального розподілу лежать в межах\(\pm 1s\) середнього, 95% лежать в межах\(\pm\) 1,96, а 99,865% лежать всередині\(\pm 3s\). Це звичайна практика в багатьох авіаційних конструкціях приймати\(\overline{\sigma_f} - 3s\) як безпечну міцність руйнування руйнування; тоді майже 99,9% всіх зразків матимуть міцність принаймні таку високу. Це насправді не означає, що одне з кожної тисячі крил літака небезпечно; в точності теорії 0,1% є незначним числом, і 3\(s\) толерантність включає по суті всю популяцію («Шість сигм» стала популярною метою у виробництві, що означає, що тільки одна частина з приблизно мільярд не буде відповідати специфікації.). Необхідність зменшення середньої міцності\(3s\) в дизайні може бути справжнім штрафом для передових матеріалів, таких як композити, які мають високу міцність, але також високу мінливість через те, що їх методи обробки є відносно нерозробленими. Це основний фактор, що обмежує частку ринку цих передових матеріалів.

Крім візуальної перевірки лінійності графіка ймовірності, кілька тестів «доброзичливості» доступні для оцінки ступеня, в якій популяція може бути обґрунтовано визначена нормальною (або якоюсь іншою) функцією розподілу. Для цієї мети часто використовують тест «Чі-квадрат». Тут тестова статистика, яка вимірює, наскільки спостережувані дані відхиляються від очікуваних від нормального розподілу або будь-якого іншого запропонованого розподілу, є
де\(n_i\) кількість зразків, які фактично не досягли приросту міцності,\(\Delta \sigma_{f,i}, N\) - це загальна кількість зразків, і\(p_i\) це ймовірність, що очікується від передбачуваного розподілу зразка, що має силу в цьому збільшенні.
Приклад\(\PageIndex{3}\)
Щоб застосувати тест Chi-квадрат до нашої 30-тестової популяції, ми починаємо з підрахунку кількості сильних сторін, що падають у вибраних приростах сили, так само, як якщо б ми будували гістограму. Ми вибираємо п'ять кроків, щоб отримати розумні підрахунки в кожному кроці. Число, яке очікується падіння в кожному збільшенні, визначається з звичайної таблиці pdf, а квадрат різниці обчислюється.
| Нижня межа | Верхня межа | Спостережувана частота | Очікувана частота | Чісквар |
|---|---|---|---|---|
| 0 | 69.33 | 7 | 5.9 | 0,198 |
| 69.33 | 72.00 | 5 | 5.8 | 0,116 |
| 72.00 | 74.67 | 8 | 6.8 | 0,214 |
| 74.67 | 77.33 | 2 | 5.7 | 2.441 |
| 77.33 | \(\infty\) | 8 | 5.7 | 0.909 |
| \(\chi^2 = 3.878\) |
Кількість ступенів свободи для цього тесту Chi-квадрат дорівнює 4; це кількість приростів менше одиниці, оскільки у нас є обмеження, що\(n_1 + n_2 + n_3 + n_5 = 30\).
Інтерполяючи в таблиці розподілу Chi-Square (таблиця 3 у Додатку), ми виявляємо, що частка 0,44 нормально розподілених популяцій може мати\(\chi^2\) статистику до 3,88. Отже, здається розумним, що наше населення можна розглядати як нормально розподілене.
Зазвичай ми задаємо питання навпаки: чи обчислюється\(\chi^2\) настільки велика, що лише мала частка - скажімо, 5% - нормально розподілених популяцій матиме\(\chi^2\) значення, такі високі чи більші? Якщо так, ми б відкинули гіпотезу про те, що наше населення нормально розподілене.
З\(\chi^2\) таблиці читаємо, що\(\alpha = 0.05\) за\(\chi^2 = 9.488\), де\(\alpha\) знаходиться частка\(\chi^2\) населення зі значеннями\(\chi^2\) більше 9,488. Аналогічно, значення\(\chi^2\) вище 9,488 означали б, що існує менше 5% шансів, що населення, описане нормальним розподілом, матиме обчислене\(\chi^2\) значення. Наше значення 3.878 значно менше, ніж це, і ми виправдані, стверджуючи, що наші дані будуть нормально розподілені.
Кілька урядових та добровільних організацій, що виробляють стандартизацію, працювали над розробкою стандартизованих процедур генерування статистично допустимих значень майна для проектування критичних конструкцій (Військовий довідник 17B, Лабораторія технологій армійських матеріалів, частина I, Том 1, 1987.). Одна з таких процедур визначає «B-допустиму» міцність як той рівень, для якого ми маємо 95% впевненості, що 90% всіх зразків матимуть принаймні таку міцність. (Використання двох відсотків тут може бути заплутаним. Ми маємо на увазі, що якби ми вимірювали сили 100 груп, кожна з яких містить 10 зразків, принаймні 95 з цих груп мали б принаймні 9 зразків, сили яких перевищують допустиму B.) Якщо виявлено, що нормальна функція розподілу забезпечує відповідний опис сукупності, значення В-базису можна обчислити з середнього та стандартного відхилення за формулою
де\(k_b\)\(n^{-1/2}\) разів 95-й квантиль «нецентрального t-розподілу»; цей коефіцієнт табульований, але може бути наближений за формулою
Приклад\(\PageIndex{4}\)
У випадку попереднього 30-тестового прикладу,\(k_B\) обчислюється як 1.78, тому це менш консервативно, ніж\(3s\) керівництво. Значення В-базису тоді
Наявність функції розподілу дозволяє нам сказати щось про впевненість, яку ми можемо мати в тому, наскільки надійно ми виміряли середню силу, на основі обов'язково обмеженої кількості індивідуальних випробувань на міцність. Відомий і надзвичайно корисний результат в математичній статистиці стверджує, що, якщо середнє значення розподілу вимірюється\(N\) раз, розподіл коштів матиме своє стандартне відхилення\(s_m\), яке пов'язане з середнім показником основного розподілу\(s\) і числом визначення,\(N\) як
\[s_m = \dfrac{s}{\sqrt{N}}\]
Цей результат може бути використаний для встановлення обмежень довіри. Оскільки 95% всіх вимірювань нормально розподіленої популяції лежать в межах 1,96 стандартних відхилень від середнього, співвідношення\(\pm 1.96s/\sqrt{N}\)
це діапазон, в якому ми можемо очікувати 95 з 100 вимірювань середнього
падіння. Таким чином, навіть за наявності суттєвої мінливості ми можемо отримати міри середньої сили до будь-якого бажаного рівня впевненості; ми просто робимо більше вимірювань, щоб збільшити значення\(N\) у вищезазначеному співвідношенні. Часто помічені на графіках експериментальних даних «смуги помилок» не завжди маркуються, і читач повинен бути дещо обережним: зазвичай це стандартні відхилення, але вони можуть вказувати на максимальні та мінімальні значення, а іноді вони становлять 95% довірчих меж. Значення цих трьох, очевидно, зовсім інше.
Приклад\(\PageIndex{5}\)
Рівняння 6.3.4 говорить нам, що якби ми повторювали 30-тестову послідовність попереднього прикладу знову і знову (очевидно, з новими зразками кожного разу), 95% вимірюваних зразків знаходилися б в межах інтервалу
\(73.278 - \dfrac{(1.96)(4.632)}{\sqrt{30}}, 73.278 + \dfrac{(1.96)(4.632)}{\sqrt{30}} = 71.62, 74.94\)
\(t\)Розподіл
Розподіл\(t\) "", табличний в таблиці 4 Додатка, подібний до нормального розподілу, побудованого у вигляді дзвіноподібної кривої, зосередженої на середньому. Він має кілька корисних додатків для міцності даних. Коли зразків у зразку мало, t-розподіл слід використовувати на користь нормального розподілу в обмеженнях довіри обчислень. Як видно з таблиці, t-значення для 95-го процентиля та 29 ступенів свободи нашого 30-тестового зразка в прикладі 6.3.3 становить 2.045. (Кількість ступенів свободи на одиницю менше загальної кількості зразків, оскільки сума кількості зразків, що мають кожну зареєстровану силу, обмежена загальною кількістю зразків.) Фактор 2.045 замінює 1,96 у цьому прикладі, без особливих змін обчислюваних обмежень довіри. Зі збільшенням кількості екземплярів t-значення наближається до 1,96. Для меншої кількості екземплярів коефіцієнт істотно відхиляється від 1,96; це 2.571 для\(n = 5\) і 3.182 для\(n = 3\).
\(t\)Розподіл також корисний для прийняття рішення про те, чи два тестові вибірки вказують на значні відмінності в популяціях, з яких вони взяті, або чи будь-яка різниця, скажімо, засобів двох вибірки може бути приписана очікуваним статистичним варіаціям у тому, що два по суті ідентичні. популяцій. Наприклад, на малюнку 3 показана сукупна ймовірність руйнування графіто-епоксидних зразків, випробуваних при трьох різних температурах, і виявляється, що середня міцність дещо знижується високими температурами і навіть більше низькими температурами. Але чи ці відмінності реальні, або просто статистичний розкид?
На це питання можна відповісти, обчисливши значення для\(t\) використання засобів і стандартних відхилень будь-яких двох зразків, за формулою
\[t = \dfrac{|\bar{\sigma} f_1 - \bar{\sigma} f_2|}{\sqrt{\dfrac{s_1^2}{n_1 - 1} + \dfrac{s_2^2}{n_2 - 1}}}\]
Ця статистика, як відомо, має\(t\) розподіл, якщо відхилення\(s_1\) і\(s_2\) не надто відрізняються. Середнє і стандартне відхилення\(-59^{\circ} C\) даних, показаних на малюнку 3, складають 65.03 і 5.24 відповідно. Використовуючи рівняння 5 для порівняння кімнатної температури (\(23^{\circ} C\)) та\(-59^{\circ} C\) даних,\(t\) -statistic дорівнює
\(t = \dfrac{(73.28 - 65.03)}{\sqrt{\dfrac{(4.63)^2}{29} + \dfrac{(5.24)^2}{29}}} = 6.354\)
З таблиці 4 в Додатку ми тепер шукаємо значення\(t\) для 29 ступенів свободи, що відповідає 95% (або якомусь іншому значенню, за бажанням) населення. Ми робимо це, скануючи стовпець\(F(t) = 0.975\) замість 0,95, оскільки\(t\) розподіл симетричний і ще 0,025 частка населення лежить за межами\(t = -0.975\). \(t\)Значення для 95%\((F(t) = 0.975)\) і 29 ступенів свободи дорівнює 2.045.
Цей результат означає, що якби ми неодноразово відбирали будь-які дві довільні зразки 30 зразків з однієї популяції, 95% цих виборів мали б t-статистику, обчислену рівнянням 6.3.5 менше 2.045; лише 5% давали б більші значення\(t\). Оскільки статистика 6.354 t-для\(-59^{\circ}C\) та 23\(^{\circ} C\) вибірки набагато перевищує 2.045, ми можемо зробити висновок, що дуже малоймовірно, що два набори даних належать до однієї популяції. І навпаки, ми робимо висновок, що два набори даних насправді є статистично незалежними, і що температура має статистично значущий вплив на силу.
Розподіл Вейбулла
Великі зразки, як правило, мають нижчу середню міцність, ніж малі, просто тому, що великі, швидше за все, містять недолік, досить великий, щоб викликати перелом при даному прикладному напрузі. Цей ефект можна виміряти безпосередньо, наприклад, шляхом побудови міцності волокон проти окружності волокна, як на малюнку 4. З аналогічних причин крихкі матеріали, як правило, мають більш високу міцність при випробуванні на вигин, ніж при розтягуванні, оскільки при вигині напруги зосереджені в меншій області біля зовнішніх поверхонь.

Гіпотеза ефекту розміру призвела до значних зусиль у розвитку спільноти статистичного аналізу 1930-х і 40-х років, причому, мабуть, найбільш помітним внеском є те, що W. Weibull (Див. B. Epstein, J. Appl. Phys., Vol. 19, p. 140, 1948 для корисного огляду статистичної обробки ефекту розміру при переломі та для резюме статистики екстремальних значень, застосованих до проблем перелому.) у 1939 році. Вейбулл постулював, що ймовірність виживання при стресі\(\sigma\), тобто ймовірність того, що обсяг зразка не містить недолік, досить великий, щоб вийти з ладу під напругою\(\sigma\), може бути записана у формі
\[P_s(\sigma) = \exp [-(\dfrac{\sigma}{\sigma_0})^m]\]
Вейбулл вибрав форму цього виразу для його математичної зручності, а не деякого фундаментального розуміння, але протягом багатьох випробувань було виявлено, щоб добре описати статистику перелому. Параметри\(\sigma_0\) і\(m\) є регульованими константами; на малюнку 5 показана форма функції Вейбулла для двох значень параметра\(m\). Матеріали з більшою мінливістю мають менші значення\(m\); стали мають\(m \approx 100\), в той час як кераміка мають\(m \approx 10\). Цей параметр може бути пов'язаний з коефіцієнтом варіації; до розумного наближення,\(m \approx 1.2/C.V.\)

Варіацію на нормальній ймовірності паперового графічного методу, викладеного раніше, можна розробити, взявши логарифми рівняння 6.3.6:
\(\begin{array} {rcl} {\ln P_s} & = & {-(\dfrac{\sigma}{\sigma_0})^m} \\ {\ln (\ln P_s)} & = & {-m \ln (\dfrac{\sigma}{\sigma_0})} \end{array}\)
Звідси подвійний логарифм ймовірності перевищення тієї чи іншої сили в\(\sigma\) порівнянні з логарифмом сили повинен будуватися як пряма лінія з нахилом\(m\).
Приклад\(\PageIndex{6}\)
Знову використовуючи 30-тестовий зразок попередніх прикладів, оцінку\(\sigma_0\) параметра можна отримати шляхом побудови ймовірності виживання (1 мінус ранг) і відзначивши значення σ f, при якому падає Ps\(1/e = 0.37\); це дає\(\sigma_0 \approx 74\). (Більш точний метод регресії дає 75.46.) Табуляція подвійного логарифма\(P_s\) проти логарифма з\(\sigma_f/\sigma_0\) то
| \(i\) | \(\sigma_{f,i}\) | \(\ln \ln (1/P_s)\) | \(\ln (\sigma_{f,i}/\sigma_0)\) |
|---|---|---|---|
| \ (i\) ">1 | \ (\ сигма_ {f, i}\) ">65.50 | \ (\ ln\ ln (1/p_s)\) ">-3.4176 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.1416 |
| \ (i\) ">2 | \ (\ сигма_ {f, i}\) ">65.67 | \ (\ ln\ ln (1/p_s)\) ">-2.7077 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.1390 |
| \ (i\) ">3 | \ (\ сигма_ {f, i}\) ">67.03 | \ (\ ln\ ln (1/p_s)\) ">-2.2849 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.1185 |
| \ (i\) ">4 | \ (\ сигма_ {f, i}\) ">67.84 | \ (\ ln\ ln (1/p_s)\) ">-1.9794 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.1065 |
| \ (i\) ">5 | \ (\ сигма_ {f, i}\) ">67,95 | \ (\ ln\ ln (1/p_s)\) ">-1.7379 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.1048 |
| \ (i\) ">6 | \ (\ сигма_ {f, i}\) ">68.10 | \ (\ ln\ ln (1/P_s)\) ">-1.5366 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.1026 |
| \ (i\) ">7 | \ (\ сигма_ {f, i}\) ">69.20 | \ (\ ln\ ln (1/p_s)\) ">-1,3628 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0866 |
| \ (i\) ">8 | \ (\ сигма_ {f, i}\) ">70.65 | \ (\ ln\ ln (1/p_s)\) ">-1.2090 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0659 |
| \ (i\) ">9 | \ (\ сигма_ {f, i}\) ">71.04 | \ (\ ln\ ln (1/p_s)\) ">-1.0702 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0604 |
| \ (i\) ">10 | \ (\ сигма_ {f, i}\) ">71.17 | \ (\ ln\ ln (1/p_s)\) ">-0,9430 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0585 |
| \ (i\) ">11 | \ (\ сигма_ {f, i}\) ">71.53 | \ (\ ln\ ln (1/p_s)\) ">-0,8250 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0535 |
| \ (i\) ">12 | \ (\ сигма_ {f, i}\) ">71.75 | \ (\ ln\ ln (1/p_s)\) ">-0.7143 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0504 |
| \ (i\) ">13 | \ (\ сигма_ {f, i}\) ">72.28 | \ (\ ln\ ln (1/p_s)\) ">-0,6095 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0431 |
| \ (i\) ">14 | \ (\ сигма_ {f, i}\) ">72.29 | \ (\ ln\ ln (1/p_s)\) ">-0.5095 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0429 |
| \ (i\) ">15 | \ (\ сигма_ {f, i}\) ">72.50 | \ (\ ln\ ln (1/p_s)\) ">-0.4134 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0400 |
| \ (i\) ">16 | \ (\ сигма_ {f, i}\) ">72.85 | \ (\ ln\ ln (1/p_s)\) ">-0.3203 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0352 |
| \ (i\) ">17 | \ (\ сигма_ {f, i}\) ">72.85 | \ (\ ln\ ln (1/p_s)\) ">-0,2295 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0352 |
| \ (i\) ">18 | \ (\ сигма_ {f, i}\) ">73.23 | \ (\ ln\ ln (1/p_s)\) ">-0.1404 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0300 |
| \ (i\) ">19 | \ (\ сигма_ {f, i}\) ">73.80 | \ (\ ln\ ln (1/p_s)\) ">-0.0523 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0222 |
| \ (i\) ">20 | \ (\ сигма_ {f, i}\) ">74.28 | \ (\ ln\ ln (1/p_s)\) ">0.0355 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0158 |
| \ (i\) ">21 | \ (\ сигма_ {f, i}\) ">75.33 | \ (\ ln\ ln (1/p_s)\) ">0.1235 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">-0.0017 |
| \ (i\) ">22 | \ (\ сигма_ {f, i}\) ">75.78 | \ (\ ln\ ln (1/p_s)\) ">0,2125 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0042 |
| \ (i\) ">23 | \ (\ сигма_ {f, i}\) ">77.81 | \ (\ ln\ ln (1/p_s)\) ">0.3035 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0307 |
| \ (i\) ">24 | \ (\ сигма_ {f, i}\) ">77.81 | \ (\ ln\ ln (1/p_s)\) ">0,3975 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0307 |
| \ (i\) ">25 | \ (\ сигма_ {f, i}\) ">77.90 | \ (\ ln\ ln (1/p_s)\) ">0.4961 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0318 |
| \ (i\) ">26 | \ (\ сигма_ {f, i}\) ">79.08 | \ (\ ln\ ln (1/p_s)\) ">0.6013 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0469 |
| \ (i\) ">27 | \ (\ сигма_ {f, i}\) ">79.83 | \ (\ ln\ ln (1/p_s)\) ">0.7167 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0563 |
| \ (i\) ">28 | \ (\ сигма_ {f, i}\) ">79.92 | \ (\ ln\ ln (1/P_s)\) ">0.8482 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0574 |
| \ (i\) ">29 | \ (\ сигма_ {f, i}\) ">80.52 | \ (\ ln\ ln (1/p_s)\) ">1.0083 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0649 |
| \ (i\) ">30 | \ (\ сигма_ {f, i}\) ">82.84 | \ (\ ln\ ln (1/p_s)\) ">1.2337 | \ (\ ln (\ сигма_ {f, i}/\ сигма_0)\) ">0.0933 |
Графік Вейбуля цих даних показаний на малюнку 6; нахил регресії - 17,4.

Аналогічно конструкції В-базису, допустимої для нормального розподілу, B-допустимий також може бути обчислений за параметрами Вейбулла\(m\) і\(\sigma_0\). Процедура є (S.W. іржа та ін., ASTM STP 1003, стор. 136, 1989. (Також військовий довідник 17.)
\(B = Q \exp [\dfrac{-V}{m\sqrt{N}}]\)
де\(Q\) і\(V\) знаходяться
\(Q = \sigma_0 (0.10536)^{1/m}\)
Приклад\(\PageIndex{7}\)
B-допустимий обчислюється для 30-тестової популяції як
\(Q = 75.46 (0.10536)^{1/17.4m} = 66.30\)
\(B = 66.30 \exp [\dfrac{-5.03}{17.4\sqrt{30}}] = 62.89\)
Це значення дещо нижче 65,05, отриманого як нормального розподілу B-допустимого, тому в цьому випадку метод Вейбулла трохи поблажливіший.
Рівняння Вейбуля може бути використано для прогнозування величини ефекту розміру. Якщо, наприклад, взяти еталонний том\(V_0\) і висловити обсяг довільного зразка як\(V = nV_0\), то ймовірність відмови при гучності\(V\) знаходить множенням на сам\(P_s(V)\) по собі\(n\) раз:
\(P_s (V) = [P_s(V_0)]^n = [P_s(V_0)]^{V/V_0}\)
\[P_s(V) = \exp -\dfrac{V}{V_0} (\dfrac{\sigma}{\sigma_0})^m\]
Звідси ймовірність відмови зростає експоненціально з об'ємом зразка. Це ще одна небезпека в простому масштабуванні, за межами аргументу площі проти обсягу, який ми окреслили в Модулі 1.
Приклад\(\PageIndex{8}\)
Розв'язуючи рівняння 6.3.7, напруга для заданої ймовірності виживання дорівнює
\(\sigma= [\dfrac{-\ln (P_s)}{(V/V_0)}]^{\tfrac{1}{n}} \sigma_0\)
Використовуючи\(\sigma_0 = 75.46\) і\(n = 17.4\) для 30-зразкової популяції, стрес для\(P_s = .5\) і\(V/V_0 = 1\) є\(\sigma = 73.9\text{kpsi}\). Якщо зараз розмір зразка подвоюється, так що ймовірність виживання при цьому напрузі\(V/V_0 = 2\), заданому рівнянням 6.3.7, падає до\(P_s = 0.25\). Якщо, з іншого боку, розмір зразка зменшується вдвічі\((V/V_0 = 0.5)\), ймовірність виживання зростає до\(P_s = 0.71\).
Заключна нота обережності, трохи уздовж знаменитого афоризму Марка Твена про те, що існує «брехня, проклята брехня та статистика»: часто вірно, що популяції простих розтягуючих або інших лабораторних зразків можуть бути добре описані класичними статистичними розподілами. Це не слід приймати, щоб мати на увазі, що більш складні конструкції, такі як мости та літаки, можуть бути настільки акуратно описані. Наприклад, одне дослідження літака, яке цитує Гордон (J.E. Gordon, Structures, Plenum Press, 1978.) виявило, що невдачі відбуваються випадковим чином і рівномірно в широкому діапазоні, що розширюється як вище, так і нижче статистично заснованої конструкції безпечного навантаження. Будь-яка реальна конструкція, особливо для конструкцій, які ставлять під загрозу життя людини, повинна бути перевірена всіма розумними способами, які інженер може собі уявити. Це буде включати перевірку доказів на відмову, врахування найгірших можливих факторів навколишнього середовища, врахування будівельних помилок, що виникають внаслідок складних у виготовленні конструкцій, і так далі майже без обмежень. Досвід, обережність і здоровий глузд зазвичай будуть не менш важливими, як складні числові розрахунки.
Вправа\(\PageIndex{1}\)
Десять вимірів міцності дали середню міцність на розрив\(\overline{\sigma_f} = 100\) МПа, з 95% довірчих меж\(\pm 8\) МПа. Скільки додаткових вимірювань буде потрібно для зменшення довірчих меж вдвічі, припускаючи, що середнє і стандартне відхилення вимірювань залишаються незмінними?
Вправа\(\PageIndex{2}\)
Тридцять вимірювань міцності на розрив графіту/епоксидного композиту, перерахованих у прикладі,\(\PageIndex{1}\) були зроблені при кімнатній температурі. Тридцять додаткових випробувань, проведених при 93,\(^{\circ} C\) дали значення (в кпсі): 63,40, 69,70, 72,80, 63,60, 71,20, 72,07, 76,97, 70,94, 76,22, 64,65, 61,08, 61,53, 72.88, 74.90, 78.61, 68.72, 72.87, 64.49, 75.12, 67.80, 72.68, 75.09, 67.23, 64.80, 75.84, 63.87, 72.46, 69.54, 76.97. Для цих даних:
- Визначте середнє арифметичне, стандартне відхилення та коефіцієнт варіації.
- Визначте 95% довірчі межі на середню міцність.
- Визначте, чи відрізняються середні сили в 23\(^{\circ} C\) і 93\(^{\circ} C\) статистично.
- Визначте нормальну і Вейбулла В-допустимі сили.
- Побудувати сукупну ймовірність відмови\(P_f\) проти напруги відмови на нормальній ймовірності паперу.
- Чи здається, що дані розподіляються нормально, на основі\(\chi^2\) тесту?
- Побудуйте кумулятивну ймовірність виживання\(P_s\) та напругу невдачі на папері ймовірності Вейбулла.
- Визначте параметри Вейбуля\(\sigma_0\) і\(m\).
- Оцініть, як змінилася б середня міцність, якби зразки були зроблені в десять разів менше, або в десять разів більше.
Вправа\(\PageIndex{3}\)
Повторіть попередню проблему, але використовуючи дані для -59◦ C: 55.62, 55.91, 56.73, 57.54, 58.28, 59.23, 60.39, 60.62, 61.1, 62.1, 63.69, 63.8, 64.7, 65.33, 66.39, 66.43, 66.72, 67.05, 67.76, 68.84, 68.84 9.15, 69.3, 69.37, 69.82, 70.94, 71.39, 71.74, 72.2, 73.46.
Додаток - Статистичні таблиці та папір
Нижче наведено кілька стандартних таблиць і графічних документів, які можуть бути використані при виконанні статистичних розрахунків, у випадку, якщо відповідне програмне забезпечення недоступне.
1. Звичайна таблиця розподілу
2. Сукупна таблиця нормального розподілу
3. Chi-Квадратний стіл
4. \(t\)-Розподіл
5. Нормальна ймовірність паперу
6. Вейбулл Папір
1. Нормальний розподіл

2. Сукупний нормальний розподіл


4. \(t\)-Розподіл

5. Нормальна ймовірність паперу

6. Вейбулл Папір

