10.2: Функція випадкових векторів
- Page ID
- 98489
Вступ
Загальний підхід відображення для однієї випадкової величини та дискретної альтернативи поширюється на функції більш ніж однієї змінної. Зручно розглядати випадок двох випадкових величин, розглянутих спільно. Розширення до більш ніж двох випадкових величин робляться аналогічно, хоча деталі більш складні.
Загальний підхід поширився на пару
Розглянемо пару,\(\{X, Y\}\) що має спільний розподіл на площині. Підхід аналогічний такому для однієї випадкової величини з розподілом по лінії.
Щоб знайти\(P((X, Y) \in Q)\).
- Картографічний підхід. Просто знайдіть величину маси ймовірності, відображеної в множині\(Q\) на площині випадковим вектором\(W = (X, Y)\).
- У абсолютно безперервному випадку розрахуйте\(\int \int_Q f_{XY}\).
- У дискретному випадку визначте ті векторні\((t_i, u_j)\) значення\((X, Y)\) яких є в множині\(Q\) і додайте пов'язані з ними ймовірності.
- Дискретна альтернатива. Розглянемо кожне\((t_i, u_j)\) векторне значення\((X, Y)\). Виберіть ті, які відповідають визначальним умовам,\(Q\) і додайте пов'язані з ними ймовірності. Саме такий підхід ми використовуємо в розрахунках MATLAB. При цьому не потрібно, щоб ми описували геометрично регіон\(Q\).
Щоб знайти\(P(g(X,Y) \in M)\). \(g\)є реальною цінністю і\(M\) є підмножиною реальної лінії.
- Картографічний підхід. Визначте\(Q\)\(M\) набір усіх тих,\((t, u)\) які відображені функцією\(g\). Зараз
\(W(\omega) = (X(\omega), Y(\omega)) \in Q\)IFF\(g((X(\omega), Y(\omega)) \in M\) Отже
\(\{\omega: g(X(\omega), Y(\omega)) \in M\} = \{\omega: (X(\omega), Y(\omega)) \in Q\}\)
Оскільки це одна і та ж подія, вони повинні мати однакову ймовірність. Як тільки\(Q\) ідентифікується на площині, визначте\(P((X, Y) \in Q)\) в звичайному порядку (див. Частина а, вище).
- Дискретна альтернатива. Для кожного можливого векторного\((t_i, u_j)\) значення\((X, Y)\), визначити, чи\(g(t_i, u_j)\) відповідає визначальна умова для\(M\). Виберіть ті\((t_i, u_j)\), які роблять, і додайте пов'язані ймовірності.
Ми ілюструємо картографічний підхід в абсолютно безперервному випадку. Ключовим елементом у підході є знаходження набору\(Q\) на площині таким чином, що\(g(X, Y) \in M\) iff\((X, Y) \in Q\). Бажана ймовірність виходить шляхом інтеграції\(f_{XY}\) над\(Q\).
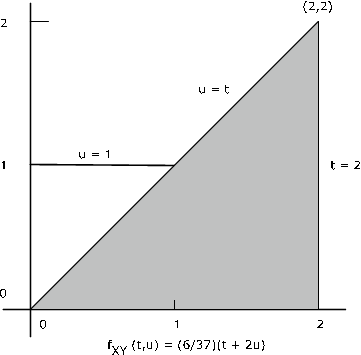
Приклад 10.2.15. Числовий приклад
Пара\(\{X, Y\}\) має щільність стику\(f_{XY} (t, u) = \dfrac{6}{37} (t + 2u)\) на області,\(t = 0\) обмеженій\(t = 2\),\(u = 0\),,\(u = \text{max} \{1, t\}\) (див. Рис. Визначте\(P(Y \le X) = P(X - Y \ge 0)\). Ось\(g(t, u) = t - u\) і\(M = [0, \infty)\). Тепер\(Q = \{(t, u) : t - u \ge 0\} = \{(t, u) : u \le t \}\) яка область на площині на або нижче лінії\(u = t\). Експертиза малюнка показує, що для цієї області,\(f_{XY}\) відрізняється від нуля на трикутник, обмежений\(t = 2\)\(u = 0\), і\(u = t\). Бажана ймовірність
\(P(Y \le X) = \int_{0}^{2} \int_{0}^{t} \dfrac{6}{37} (t + 2u) du\ dt = 32/37 \approx 0.8649\)
Приклад 10.2.16. Щільність для суми X + Y
Припустимо, пара\(\{X, Y\}\) має щільність стику\(f_{XY}\). Визначаємо щільність для
\(Z = X + Y\)
Рішення
\(F_Z (v) = P(X + Y \le v) = P((X, Y) \in Q_v)\)де\(Q_v = \{(t, u) : t + u \le v\} = \{(t, u): u \le v - t\}\)
Для будь-якого фіксованого\(v\) область\(Q_v\) - це ділянка площини на або нижче лінії\(u = v - t\) (див. Рис. Таким чином
\(F_Z (v) = \int \int_{Q} f_{XY} = \int_{-\infty}^{\infty} \int_{-\infty}^{v - t} f_{XY} (t, u) du\ dt\)
Диференціюючи за допомогою фундаментальної теореми числення, отримаємо
\(f_Z (v) = \int_{\infty}^{\infty} f_{XY} (t, v - t)\ dt\)
Це інтегральне вираження відоме як інтеграл згортки.
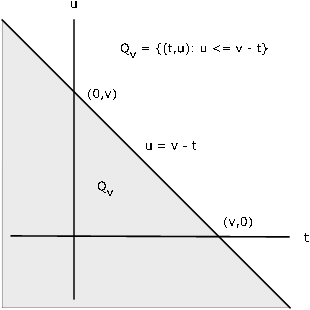
Малюнок 10.2.2. Регіон\(Q_v\) для\(X + Y \le v\).
Приклад 10.2.17. Сума спільних однорідних випадкових величин
Припустимо, пара\(\{X, Y\}\) має спільну рівномірну щільність на одиничному квадраті\(0 \le t \le 1, 0 \le u \le 1\).. Визначаємо щільність для\(Z = X + Y\).
Рішення
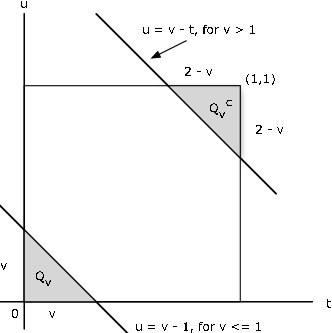
\(F_Z (v)\)це ймовірність в регіоні\(Q_v: u \le v - t\). Тепер\(P_{XY} (Q_v) = 1 - P_{XY} (Q_{v}^{c})\), де\(Q_{v}^{c}\) комплементарним набором є безліч точок над лінією. Як показано на малюнку 3, для\(v \le 1\), частина\(Q_v\) якої має імовірнісну масу, є нижня затінена трикутна область на малюнку, яка має площу (а значить і ймовірність)\(v^2\) /2. Для\(v\) > 1 додатковою областю\(Q_{v}^{c}\) є верхня затінена область. Він має площу\((2 - v)^2/2\). так що в даному випадку\(P_{XY} (Q_v) = 1 - (2 - v)^2/2\). Таким чином,
\(F_Z (v) = \dfrac{v^2}{2}\)для\(0 \le v \le 1\) і\(F_Z (v) = 1 - \dfrac{(2 - v)^2}{2}\) для\(1 \le v \le 2\)
Диференціація показує, що\(Z\) має симетричний трикутний розподіл на [0, 2], оскільки
\(f_Z (v) = v\)для\(0 \le v \le 1\) і\(f_Z(v) = (2 - v)\) для\(1 \le v \le 2\)
За допомогою індикаторних функцій вони можуть бути об'єднані в єдиний вираз
\(f_Z (v) = I_{[0, 1]} (v) v + I_{(1, 2]} (2 - v)\)
АЛЬТЕРНАТИВНЕ рішення
З тих пір\(f_{XY} (t, u) = I_{[0, 1]} (t) I_{[0, 1]} (u)\), у нас є\(f_{XY} (t, v - t) = I_{[0, 1]} (t) I_{[0, 1]} (v - t)\). Тепер\(0 \le v - t \le 1\) іфф\(v - 1 \le t \le v\), так що
\(f_{XY} (t, v - t) = I_{[0, 1]} (v) I_{[0, v]} (t) + I_{(1, 2]} (v) I_{[v - 1, 1]} (t)\)
Інтеграція щодо\(t\) дає результат вище.
Незалежність функцій незалежних випадкових величин
Припустимо,\(\{X, Y\}\) це незалежна пара. Нехай\(Z = g(X), W = h(Y)\). Так як
\(Z^{-1} (M) = X^{-1} [g^{-1} (M)]\)і\(W^{-1} (N) = Y^{-1} [h^{-1} (N)]\)
пара\(\{Z^{-1} (M), W^{-1} (N)\}\) незалежна для кожної пари\(\{M, N\}\). Таким чином, пара\(\{Z, W\}\) незалежна.
Якщо\(\{X, Y\}\) незалежна пара і\(Z = g(X)\)\(W = g(X)\),\(\{Z, W\}\) то пара незалежна. Однак якщо\(Z = g(X, Y)\) і\(W = h(X, Y)\), то взагалі не\(\{Z, W\}\) є самостійним. Це проілюстровано для простих випадкових величин за допомогою m-процедури jointzw в кінці наступного розділу.
Приклад 10.2.18. Незалежність простих наближень до незалежної пари
Припустимо,\(\{X, Y\}\) це незалежна пара з простими наближеннями\(X_s\) і\(Y_s\) як описано в розділі Наближення розподілу.
\(X_s = \sum_{i = 1}^{n} t_i I_{E_i} = \sum_{i = 1}^{n} t_i I_{M_i} (X)\)і\(Y_s = \sum_{j = 1}^{m} u_j I_{F_j} = \sum_{j = 1}^{m} u_j I_{N_j} (Y)\)
Як функції\(X\) і\(Y\), відповідно, пара\(\{X_s, Y_s\}\) незалежна. Також кожна пара\(\{I_{M_i}(X), I_{N_j} (Y)\}\) незалежна.
Використання MATLAB на парах простих випадкових величин
В однозмінному випадку ми використовуємо операції масиву над значеннями,\(X\) щоб визначити матрицю значень\(g(X)\). У двозмінному випадку ми повинні використовувати операції масиву на обчислювальних матрицях\(t\) і\(u\) отримати матрицю, елементами\(G\) якої є\(g(t_i, u_j)\). Для отримання розподілу для\(Z = g(X, Y)\) ми можемо використовувати m-функцію csort on\(G\) та спільну матрицю ймовірностей\(P\). Потім першим кроком є використання jcalc або icalc для налаштування спільного розподілу та обчислювальних матриць. Це проілюстровано на наступному прикладі.
Приклад 10.2.19.
% file jdemo3.m
% data for joint simple distribution
X = [-4 -2 0 1 3];
Y = [0 1 2 4];
P = [0.0132 0.0198 0.0297 0.0209 0.0264;
0.0372 0.0558 0.0837 0.0589 0.0744;
0.0516 0.0774 0.1161 0.0817 0.1032;
0.0180 0.0270 0.0405 0.0285 0.0360];
jdemo3 % Call for data
jcalc % Set up of calculating matrices t, u.
Enter JOINT PROBABILITIES (as on the plane) P
Enter row matrix of VALUES of X X
Enter row matrix of VALUES of Y Y
Use array operations on matrices X, Y, PX, PY, t, u, and P
G = t.^2 -3*u; % Formation of G = [g(ti,uj)]
M = G >= 1; % Calculation using the XY distribution
PM = total(M.*P) % Alternately, use total((G>=1).*P)
PM = 0.4665
[Z,PZ] = csort(G,P);
PM = (Z>=1)*PZ' % Calculation using the Z distribution
PM = 0.4665
disp([Z;PZ]') % Display of the Z distribution
-12.0000 0.0297
-11.0000 0.0209
-8.0000 0.0198
-6.0000 0.0837
-5.0000 0.0589
-3.0000 0.1425
-2.0000 0.1375
0 0.0405
1.0000 0.1059
3.0000 0.0744
4.0000 0.0402
6.0000 0.1032
9.0000 0.0360
10.0000 0.0372
13.0000 0.0516
16.0000 0.0180
Ми розширюємо приклад вище, розглядаючи функцію\(W = h(X, Y)\), яка має складене визначення.
Приклад 10.2.20. Продовження прикладу 10.2.19
Нехай
\(W = \begin{cases} X & \text{ for } X + Y \ge 1 \\ X^2 + Y^2 & \text{ for } X + Y < 1 \end{cases}\)Визначаємо розподіл для\(W\)
H = t.*(t+u>=1) + (t.^2 + u.^2).*(t+u<1); % Specification of h(t,u)
[W,PW] = csort(H,P); % Distribution for W = h(X,Y)
disp([W;PW]')
-2.0000 0.0198
0 0.2700
1.0000 0.1900
3.0000 0.2400
4.0000 0.0270
5.0000 0.0774
8.0000 0.0558
16.0000 0.0180
17.0000 0.0516
20.0000 0.0372
32.0000 0.0132
ddbn % Plot of distribution function
Enter row matrix of values W
Enter row matrix of probabilities PW
print % See Figure 10.2.4
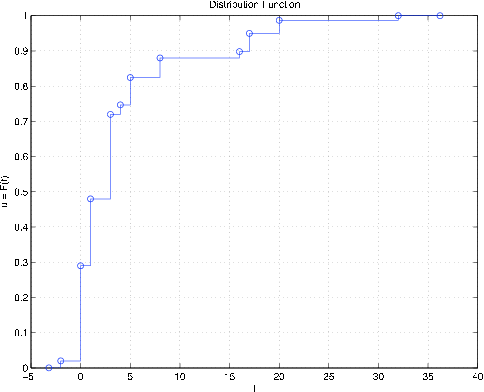
Малюнок 10.2.4. Розподіл випадкової\(W\) величини в прикладі 10.2.20.
Спільні розподіли для двох функцій\((X, Y)\)
У попередніх процедурах ми використовуємо csort для отримання граничного розподілу для однієї функції\(Z = g(X, Y)\). Часто бажано мати спільний розподіл на пару\(Z = g(X, Y)\) і\(W = h(X, Y)\). Як особливі випадки, ми можемо мати\(Z = X\) або\(W = Y\). Припустимо
\(Z\)має значення [\(z_1\)\(z_2\)\(\cdot\cdot\cdot\)\(z_c\)] і\(W\) має значення [\(w_1\)\(w_2\)\(\cdot\cdot\cdot\)\(w_c\)]
Спільний розподіл вимагає ймовірності кожної пари,\(P(W = w_i, Z = z_j)\). Кожній такій парі значень відповідає набір пар\(Y\) значень\(X\) і. Для визначення спільної матриці ймовірностей\(PZW\) для\((Z, W)\) розташованих як на площині, ми\((i, j)\) присвоюємо кожній позиції ймовірність\(P(W = w_i, Z=z_j)\), зі значеннями\(W\) збільшення вгору. Кожна пара значень (\(W, Z\)) відповідає одній або декільком парам значень (\(Y, X\)). Якщо ми виберемо і додамо ймовірності, відповідні останнім парам, ми маємо\(P(W = w_i, Z = z_j)\). Це може бути досягнуто наступним чином:
Налаштуйте обчислювальні матриці\(t\) і\(u\) як з jcalc.
Використовуйте арифметику масиву для визначення матриць значень\(G = [g(t, u)]\) і\(H = [h(t, u)]\).
Використовуйте csort для визначення матриць\(Z\) і\(W\) значень, а також матриць\(PZ\) і\(PW\) граничних ймовірностей.
Для кожної пари використовуйте функцію MATLAB find\((w_i, z_j)\), щоб визначити позиції a, для яких
Призначити позиції (\(i, j\)) у спільній матриці ймовірностей\(PZW\) для (\(Z, W\)) ймовірності
Спочатку розглянемо основні розрахунки, які потім реалізуються в m-процедурі jointsw.
Приклад 10.2.21. Ілюстрація основних спільних розрахунків
% file jdemo7.m
P = [0.061 0.030 0.060 0.027 0.009;
0.015 0.001 0.048 0.058 0.013;
0.040 0.054 0.012 0.004 0.013;
0.032 0.029 0.026 0.023 0.039;
0.058 0.040 0.061 0.053 0.018;
0.050 0.052 0.060 0.001 0.013];
X = -2:2;
Y = -2:3;
jdemo7 % Call for data in jdemo7.m
jcalc % Used to set up calculation matrices t, u
- - - - - - - - - -
H = u.^2 % Matrix of values for W = h(X,Y)
H =
9 9 9 9 9
4 4 4 4 4
1 1 1 1 1
0 0 0 0 0
1 1 1 1 1
4 4 4 4 4
G = abs(t) % Matrix of values for Z = g(X,Y)
G =
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
[W,PW] = csort(H,P) % Determination of marginal for W
W = 0 1 4 9
PW = 0.1490 0.3530 0.3110 0.1870
[Z,PZ] = csort(G,P) % Determination of marginal for Z
Z = 0 1 2
PZ = 0.2670 0.3720 0.3610
r = W(3) % Third value for W
r = 4
s = Z(2) % Second value for Z
s = 1
Щоб визначити\(P(W = 4, Z = 1)\), нам потрібно визначити (\(t, u\)) позиції, за які береться ця пара (\(W, Z\)) значень. За допомогою огляду ми знаходимо їх (2,2), (6,2), (2,4) та (6,4). Тоді\(P(W = 4, Z = 1)\) загальна ймовірність на цих позиціях. Це 0,001 + 0,052 + 0,058 + 0,001 = 0,112. Ми ставимо цю ймовірність в спільну матрицю ймовірностей\(PZW\) у\(W = 4, Z = 1\) позиції. Це може бути досягнуто за допомогою MATLAB за допомогою наступних операцій.
[i,j] = find((H==W(3))&(G==Z(2))); % Location of (t,u) positions
disp([i j]) % Optional display of positions
2 2
6 2
2 4
6 4
a = find((H==W(3))&(G==Z(2))); % Location in more convenient form
P0 = zeros(size(P)); % Setup of zero matrix
P0(a) = P(a) % Display of designated probabilities in P
P0 =
0 0 0 0 0
0 0.0010 0 0.0580 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0.0520 0 0.0010 0
PZW = zeros(length(W),length(Z)) % Initialization of PZW matrix
PZW(3,2) = total(P(a)) % Assignment to PZW matrix with
PZW = 0 0 0 % W increasing downward
0 0 0
0 0.1120 0
0 0 0
PZW = flipud(PZW) % Assignment with W increasing upward
PZW =
0 0 0
0 0.1120 0
0 0 0
0 0 0
Процедура jointzw здійснює цю операцію для кожної можливої пари\(W\) і\(Z\) значень (при цьому операція фліпа настає тільки після того, як всі індивідуальні завдання зроблені).
приклад 10.2.22. спільний розподіл для z = g (x, y) = ||x| - y| і w = h (x, y) = |xy|
% file jdemo3.m data for joint simple distribution
X = [-4 -2 0 1 3];
Y = [0 1 2 4];
P = [0.0132 0.0198 0.0297 0.0209 0.0264;
0.0372 0.0558 0.0837 0.0589 0.0744;
0.0516 0.0774 0.1161 0.0817 0.1032;
0.0180 0.0270 0.0405 0.0285 0.0360];
jdemo3 % Call for data
jointzw % Call for m-program
Enter joint prob for (X,Y): P
Enter values for X: X
Enter values for Y: Y
Enter expression for g(t,u): abs(abs(t)-u)
Enter expression for h(t,u): abs(t.*u)
Use array operations on Z, W, PZ, PW, v, w, PZW
disp(PZW)
0.0132 0 0 0 0
0 0.0264 0 0 0
0 0 0.0570 0 0
0 0.0744 0 0 0
0.0558 0 0 0.0725 0
0 0 0.1032 0 0
0 0.1363 0 0 0
0.0817 0 0 0 0
0.0405 0.1446 0.1107 0.0360 0.0477
EZ = total(v.*PZW)
EZ = 1.4398
ez = Z*PZ' % Alternate, using marginal dbn
ez = 1.4398
EW = total(w.*PZW)
EW = 2.6075
ew = W*PW' % Alternate, using marginal dbn
ew = 2.6075
M = v > w; % P(Z>W)
PM = total(M.*PZW)
PM = 0.3390
При зазначеному в попередньому розділі, якщо\(\{X, Y\}\) це незалежна пара і\(Z = g(X)\),
\(W = h(Y)\), то пара {\(Z, W\)} є незалежною. Однак якщо\(Z = g(X, Y)\) і
\(W = h(X, Y)\), то в цілому пара {\(Z, W\)} не є незалежною. Ми можемо проілюструвати це за допомогою m-процедури jointzw
Приклад 10.2.23. Функції незалежних випадкових величин
jdemo3
itest
Enter matrix of joint probabilities P
The pair {X,Y} is independent % The pair {X,Y} is independent
jointzw
Enter joint prob for (X,Y): P
Enter values for X: X
Enter values for Y: Y
Enter expression for g(t,u): t.^2 - 3*t % Z = g(X)
Enter expression for h(t,u): abs(u) + 3 % W = h(Y)
Use array operations on Z, W, PZ, PW, v, w, PZW
itest
Enter matrix of joint probabilities PZW
The pair {X,Y} is independent % The pair {g(X),h(Y)} is independent
jdemo3 % Refresh data
jointzw
Enter joint prob for (X,Y): P
Enter values for X: X
Enter values for Y: Y
Enter expression for g(t,u): t+u % Z = g(X,Y)
Enter expression for h(t,u): t.*u % W = h(X,Y)
Use array operations on Z, W, PZ, PW, v, w, PZW
itest
Enter matrix of joint probabilities PZW
The pair {X,Y} is NOT independent % The pair {g(X,Y),h(X,Y)} is not indep
To see where the product rule fails, call for D % Fails for all pairs
Абсолютно безперервний випадок: аналіз і наближення
Як і в аналізі Joint Distributions, ми можемо встановити просте наближення до спільного розподілу і діяти як для простих випадкових величин. У цьому розділі аналітично вирішимо кілька прикладів, потім отримуємо прості наближення.
Приклад 10.2.24. Розподіл для продукту
Припустимо, пара\(\{X, Y\}\) має щільність стику\(f_{XY}\). Нехай\(Z = XY\). Визначте\(Q_v\) таке, що\(P(Z \le v) = P((X, Y) \in Q_v)\).
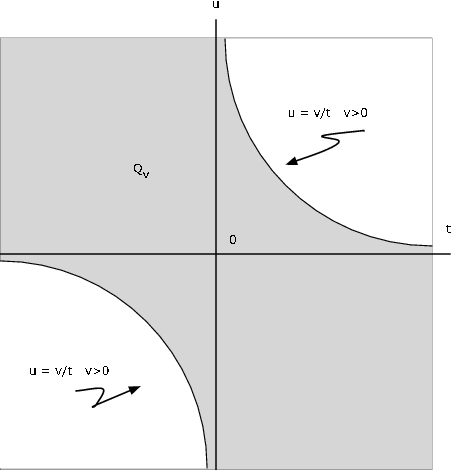
Рішення
\(Q_v = \{(t, u) : tu \le v\} = \{(t, u): t > 0, u \le v/t\} \bigvee \{(t, u) : t < 0, u \ge v/t\}\}\)
Приклад 10.2.25.
\(\{X, Y\}\)~ рівномірний на квадратній одиниці
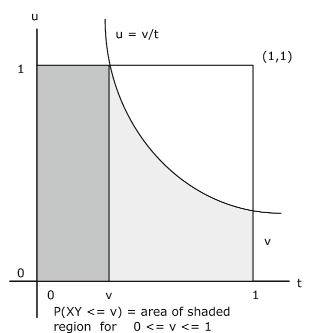
\(f_{XY} (t, u) = 1\). Потім (див. Рис. 10.2.6)
\(P(XY \le v) = \int \int_{Q_v} 1 du\ dt\)де\(Q_v = \{(t, u): 0 \le t \le 1, 0 \le u \le \text{min } \{1, v/t\}\}\)
Інтеграційні шоу
\(F_Z (v) = P(XY \le v) = v(1 - \text{ln } (v))\)щоб\(f_Z (v) = - \text{ln } (v) = \text{ln } (1/v)\),\(0 < v \le 1\)
Для\(v = 0.5\),\(F_Z (0.5) = 0.8466\).
% Note that although f = 1, it must be expressed in terms of t, u. tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (u>=0)&(t>=0) Use array operations on X, Y, PX, PY, t, u, and P G = t.*u;
[Z,PZ] = csort(G,P); p = (Z<=0.5)*PZ' p = 0.8465 % Theoretical value 0.8466, above
Приклад 10.2.26. Продовження прикладу 5 з «Випадкові вектори та спільні розподіли»
Пара\(\{X, Y\}\) має щільність стику\(f_{XY} (t, u) = \dfrac{6}{37} (t + 2u)\) на області, обмеженій\(t = 0\),\(t = 2\) і\(u = \text{max } \{1, t\}\) (див. Рис. Нехай\(Z = XY\). Визначте\(P(Z \le 1)\).
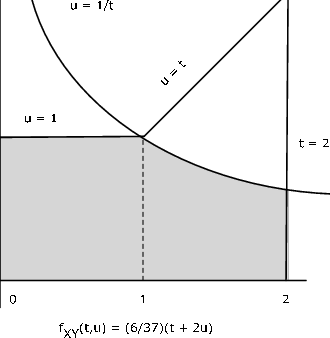
Аналітичне рішення
Посилання на малюнок 10.2.7 показує, що
\(P((X, Y) \in Q = \dfrac{6}{37} \int_{0}^{1} \int_{0}^{1} (t + 2u) du\ dt + \dfrac{6}{37} \int_{1}^{2} \int_{0}^{1/t} (t + 2u) du\ dt = 9/37 + 9/37 = 18/37 \approx 0.4865\)
ОРІЄНТОВНЕ рішення
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 300 Enter number of Y approximation points 300 Enter expression for joint density (6/37)*(t + 2*u).*(u<=max(t,1)) Use array operations on X, Y, PX, PY, t, u, and P Q = t.*u<=1; PQ = total(Q.*P) PQ = 0.4853 % Theoretical value 0.4865, above G = t.*u; % Alternate, using the distribution for Z [Z,PZ] = csort(G,P); PZ1 = (Z<=1)*PZ' PZ1 = 0.4853
У наступному прикладі функція\(g\) має складне визначення. Тобто він має різне правило для різних частин площини.
Приклад 10.2.27. З'єднана функція
Пара\(\{X, Y\}\) має щільність стику\(f_{XY} (t, u) = \dfrac{2}{3} (t + 2u)\) на одиничному\(0 \le t \le 1\) квадраті,\(0 \le u \le 1\).
\(Z = \begin{cases} X & \text{for } X^2 - Y \ge 0 \\ X + Y & \text{for } X^2 - Y < 0 \end{cases} = I_Q (X, Y) Y + I_{Q^c} (X, Y) (X + Y)\)
для\(Q = \{(t, u): u \le t^2\}\). Визначте\(P(Z <= 0.5)\).
Аналітичне рішення
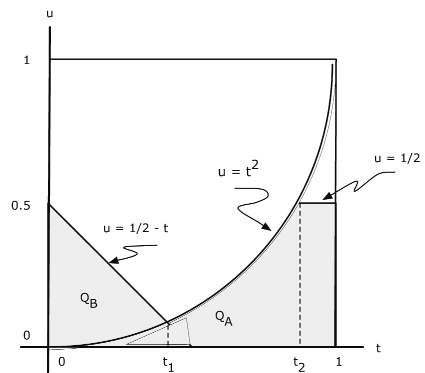
\(P(Z \le 1/2) = P(Y \le 1/2, Y \le X^2) + P(X + Y \le 1/2, Y > X^2) = P((X, Y) \in Q_A \bigvee Q_B)\)
де\(Q_A = \{(t, u) : u \le 1/2, u \le t^2\}\) і\(Q_B = \{(t, u): t + u \le 1/2, u > t^2\}\). Посилання на малюнок 10.2.8 показує, що це частина одиниці квадрата, для якої\(u \le \text{min } (\text{max } (1/2 - t, t^2), 1/2)\). Ми можемо розбити інтеграл на три частини. Нехай\(1/2 - t_1 = t_1^2\) і\(t_2^2 = 1/2\). Тоді
\(P(Z \le 1/2) = \dfrac{2}{3} \int_{0}^{t_1} \int_{0}^{1/2 - t} (t + 2u) du\ dt + \dfrac{2}{3} \int_{t_1}^{t_2} \int_{0}^{t^2} (t + 2u) du\ dt + \dfrac{2}{3} \int_{t_2}^{1} \int_{0}^{1/2} (t + 2u) du \ dt = 0.2322\)
ОРІЄНТОВНЕ рішення
tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (2/3)*(t + 2*u) Use array operations on X, Y, PX, PY, t, u, and P Q = u <= t.^2; G = u.*Q + (t + u).*(1-Q); prob = total((G<=1/2).*P) prob = 0.2328 % Theoretical is 0.2322, above
Налаштування інтегралів передбачає уважну увагу до геометрії системи. Після налаштування оцінка елементарна, але нудна. З іншого боку, наближення відбувається в прямому порядку з нормального опису проблеми. Чисельний результат досить тісно порівнюється з теоретичним значенням, а точність може бути покращена, взявши більше точок поділу.
