7.2: Наближення розподілу

Біноміальні, Пуассонові, гамма-та Гауссонові розподіли

Наближення Пуассона до біноміального розподілу

Наступне наближення є класичним. Бажаємо показати, що для маленьких$p$ і досить великих$n$

$$P(X = k) = C(n, k)p^k (1 - p)^{n - k} \approx e^{-np} \dfrac{np}{k!}$$

Припустимо,$p = \mu/n$ з$n$ великими і$\mu/n < 1$. Потім,

$$P(X = k) = C(n, k) (\mu/n)^k (1 - \mu/n)^{n-k} = \dfrac{n(n - 1) \cdot \cdot \cdot (n - k + 1)}{n^k} (1 - \dfrac{\mu}{n})^{-k} (1 - \dfrac{\mu}{n})^n \dfrac{\mu^k}{k!}$$

Перший фактор в останньому виразі - це відношення многочленів в$n$ однаковому ступені$k$, яке повинно наближатися до одиниці, оскільки$n$ стає великим. Другий фактор наближається до одного, оскільки$n$ стає великим. За добре відомою властивістю експоненціального

$$(1 - \dfrac{\mu}{n})^n \to e^{-\mu}$$

як$n \to \infty$.

В результаті виходить, що для великих$n$$P(X = k) \approx e^{-\mu} \dfrac{\mu^k}{k!}$, де$\mu = np$.

Розподіли Пуассона та Гамма

Припустимо,$Y~$ Пуассон ($\lambda t$). Тепер$X~$ гамма ($\alpha, \lambda$) iff

$$P(X \le t) = \dfrac{\lambda^{\alpha}}{\Gamma (\alpha)} \int_{0}^{1} x^{\alpha - 1} e^{-\lambda x}\ dx = \dfrac{1}{\Gamma (\alpha)} \int_{0}^{t} (\lambda x)^{\alpha - 1} e^{\lambda x} d(\lambda x) = \dfrac{1}{\Gamma (\alpha)} \int_{0}^{\lambda t} u^{\alpha - 1} e^{-\mu}\ du$$

Відомим певним інтегралом, отриманим шляхом інтеграції частинами, є

$$int_{\alpha}^{\infty} t^{n -1} e^{-t}dt = \Gamma (n) e^{-a} \sum_{k = 1}^{n - 1} \dfrac{a^k}{k!}$$

с$\Gamma (n) = (n - 1)!$.

Відзначивши, що$1 = e^{-a}e^{a} = e^{-a} \sum_{k = 0}^{\infty} \dfrac{a^k}{k!}$ ми знаходимо після деякої простої алгебри, що

$$\dfrac{1}{\Gamma(n)} \int_{0}^{a} t^{n -1} e^{-t}\ dt = e^{-a} \sum_{k = n}^{\infty} \dfrac{a^k}{k!}$$

Для$a = \lambda t$ і$\alpha = n$, ми маємо наступну рівність iff$X~$ gamma ($\alpha, \lambda$)

$$P(X \le t) = \dfrac{1}{\Gamma(n)} \int_{0}^{\lambda t} u^{n -1}d^{-u}\ du = e^{-\lambda t} \sum_{k = n}^{\infty} \dfrac{(\lambda t)^k}{k!}$$

Зараз

$$P(Y \ge n) = e^{-\lambda t} \sum_{k = n}^{\infty} \dfrac{(\lambda t)^k}{k!}$$

Ліфф$Y~$ Пуассон (м$\lambda t$.

Гаусове (нормальне) наближення

Центральна гранична теорема, про яку йдеться в обговоренні гауссового або нормального розподілу вище, говорить про те, що біноміальний і Пуассоновий розподіли повинні бути наближені гаусовим. Число успіхів у n випробуваннях має біноміальний (n, p) розподіл. Ця випадкова величина може бути виражена

$$X = \sum_{i = 1}^{n} I_{E_i}$$

Оскільки середнє значення$X$ is$np$ і дисперсія є$npq$, розподіл повинен бути приблизно$N(np, npq)$.

Малюнок 7.2.8. Гауссова апроксимація до біноміалу.

Використання генеруючої функції показує, що сума незалежних випадкових величин Пуассона дорівнює Пуассону. Тепер якщо$X~) Poisson (\(\mu$), то можна$X$ вважати суму$n$ незалежних випадкових величин, кожна Пуассона ($\mu/n$). Оскільки середнє значення і дисперсія обидва$\mu$, розумно припустити, що$X$ це приблизно$N(\mu, \mu)$.

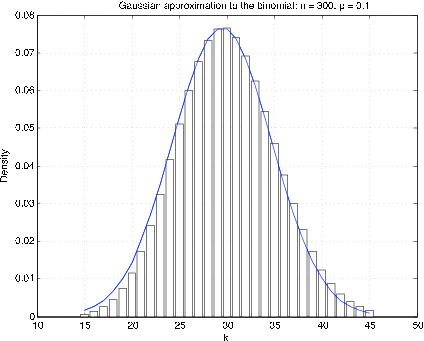
Як правило, найкраще порівнювати функції розподілу. Оскільки біноміальний і Пуассоновий розподіли є цілозначними, то виходить, що найкраще гаусове наближення виходить шляхом внесення «корекції неперервності». Щоб отримати наближення до щільності для цілозначної випадкової величини, ймовірність at$t = k$ представлена прямокутником висоти$p_k$ та одиничної ширини$k$, з середньою точкою. На малюнку 1 показаний графік «щільності» і відповідної густини Гаусса для$n = 300$,$p = 0.1$. Очевидно, що гаусова щільність компенсується приблизно на 1/2. Щоб наблизити ймовірність$X \le k$, візьміть площу під кривою від$k$ + 1/2; це називається корекцією неперервності.

Використання m-процедур для порівняння

У нас є дві m-процедури, щоб зробити порівняння. Спочатку розглянемо наближення

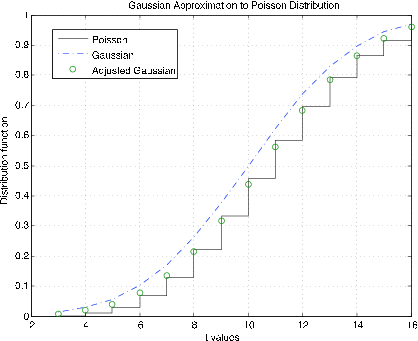
Малюнок 7.2.9. Гауссова апроксимація до функції розподілу Пуассона$\mu$ = 10.

Малюнок 7.2.10. Гауссова апроксимація до функції розподілу Пуассона$\mu$ = 100.

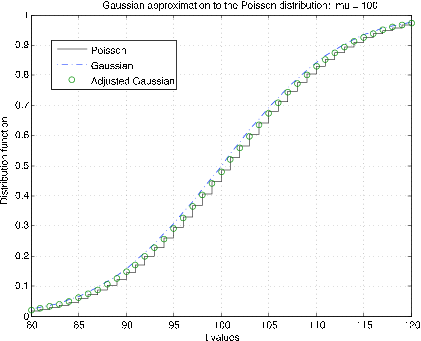
Розподіл Пуассона ($\mu$). m-процедура poissapp викликає значення$\mu$, вибирає відповідний діапазон про$k = \mu$ та відображає функцію розподілу для розподілу Пуассона (сходи) та нормального (Гаусового) розподілу (крапка тире) для$N(\mu, \mu)$. Крім того, корекція неперервності застосовується до гаусового розподілу при цілочисельних значеннях (колах). На малюнку 7.2.10 показані ділянки для$\mu$ = 10. Зрозуміло, що корекція безперервності забезпечує набагато краще наближення. Ділянки на малюнку 7.2.11 призначені для$\mu$ = 100. Тут корекція безперервності забезпечує краще наближення, але не стільки, скільки для меншого$\mu$.

Малюнок 7.2.11. Пуассона і Гаусса наближення до біноміалу:$n$ = 1000,$p$ = 0,03.

Малюнок 7.2.12. Пуассона і Гаусса наближення до біноміалу:$n$ = 50,$p$ = 0,6.

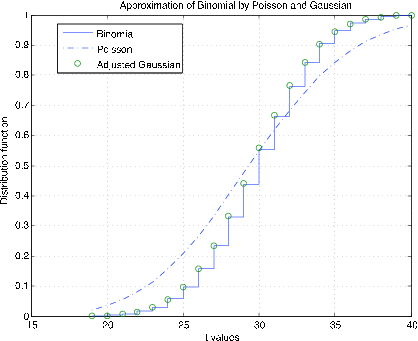
У m-процедурі bincomp порівнюються біноміальні, гаусові та Пуассонові розподіли. Викликає значення$n$ і$p$, вибирає відповідні$k$ значення та будує функцію розподілу для біноміала, безперервне наближення до функції розподілу для Пуассона, а також неперервність скоригованих значень функції розподілу за цілими значеннями. На малюнку 7.2.11 показані ділянки для$n = 1000$,$p = 0.03$. Хороша згода всіх трьох функцій розподілу очевидна. На малюнку 7.2.12 показані ділянки для$n = 50, p = 0.6$. Існує ще хороша узгодження біноміального та скоригованого гаусса. Однак розподіл Пуассона відстежує не дуже добре. Складність, як ми бачимо в одиниці дисперсії, полягає в різниці в deparances—$npq$ для біноміального порівняно з$np$ для Пуассона.

Наближення дійсної випадкової величини простими випадковими величинами

Прості випадкові величини відіграють значну роль, як в теорії, так і в додатках. В одиниці Випадкові величини ми покажемо, як визначається проста випадкова величина множиною точок на дійсній лінії, що представляють можливі значення і відповідний набір ймовірностей, за якими береться кожне з цих значень. Це описує розподіл випадкової величини і робить можливим обчислення ймовірностей подій і параметрів розподілу.

Безперервна випадкова величина характеризується сукупністю можливих значень, що поширюються безперервно по інтервалу або сукупності інтервалів. У цьому випадку ймовірність також поширюється плавно. Розподіл описується функцією щільності ймовірності, значення якої в будь-якій точці вказує «ймовірність на одиницю довжини» поблизу точки. Просте наближення отримують шляхом поділу інтервалу, який включає діапазон (набір можливих значень) на досить малі підінтервали, щоб щільність була приблизно постійною над кожним підінтервалом. Вибирається точка в кожному підінтервалі і присвоюється маса ймовірності в його підінтервалі. Поєднання обраних точок і відповідних ймовірностей описує розподіл апроксимуючої простої випадкової величини. Розрахунки, засновані на цьому розподілі, наближені відповідні розрахунки на безперервний розподіл.

Перш ніж розглядати загальну процедуру наближення, яка має значні наслідки для подальшого лікування, розглянемо кілька наочних прикладів.

Приклад$\PageIndex{10}$: Simple approximation to Poisson

Випадкова величина з розподілом Пуассона необмежена. Однак для даного значення параметра μ ймовірність для,$n$ досить велика$k \ge n$, мізерно мала. Експеримент вказує$n = \mu + 6\sqrt{\mu}$ (тобто шість стандартних відхилень понад середнє) є розумним значенням для$5 \le \mu \le 200$.

Рішення

>> mu = [5 10 20 30 40 50 70 100 150 200];
>> K = zeros(1,length(mu));
>> p = zeros(1,length(mu));
>> for i = 1:length(mu)
     K(i) = floor(mu(i)+ 6*sqrt(mu(i)));
     p(i) = cpoisson(mu(i),K(i));
end
>> disp([mu;K;p*1e6]')
    5.0000   18.0000    5.4163  % Residual probabilities are 0.000001
   10.0000   28.0000    2.2535  % times the numbers in the last column.
   20.0000   46.0000    0.4540  % K is the value of k needed to achieve
   30.0000   62.0000    0.2140  % the residual shown.
   40.0000   77.0000    0.1354  
   50.0000   92.0000    0.0668
   70.0000  120.0000    0.0359
  100.0000  160.0000    0.0205
  150.0000  223.0000    0.0159
  200.0000  284.0000    0.0133

M-процедура дискретного наближення

Якщо$X$ обмежена, абсолютно неперервна з функцією щільності$f_X$, m-процедура tappr встановлює розподіл для апроксимуючої простої випадкової величини. Інтервал, що містить діапазон$X$, ділиться на задану кількість рівних підрозділів. Маса ймовірності для кожного підінтервалу присвоюється середній точці. Якщо$dx$ довжина підінтервалів, то інтеграл функції щільності над підінтервалом наближається до$f_X(t_i) dx$. де$t_i$ - середина. По суті, графік щільності над підінтервалом наближається прямокутником довжини$dx$ і висоти$f_X(t_i)$. Після встановлення апроксимуючого простого розподілу проводяться обчислення, як для простих випадкових величин.

Приклад$\PageIndex{11}$: a numerical example

Припустимо$f_X(t) = 3t^2$,$0 \le t \le 1$. Визначте$P(0.2 \le X \le 0.9)$.

Рішення

В цьому випадку аналітичне рішення легко. $F_X(t) = t^3$на інтервалі [0, 1], так

$P = 0.9^3 - 0.2^3 = 0.7210$. Використовуємо таппр наступним чином.

>> tappr
Enter matrix [a b] of x-range endpoints  [0 1]
Enter number of x approximation points  200
Enter density as a function of t  3*t.^2
Use row matrices X and PX as in the simple case
>> M = (X >= 0.2)&(X <= 0.9);
>> p = M*PX'
p  =  0.7210

Через регулярності щільності і кількості точок наближення результат цілком добре узгоджується з теоретичним значенням.

Наступний приклад - більш складний. Зокрема, розподіл не обмежений. Однак легко визначити межу, за якою ймовірність мізерно мала.

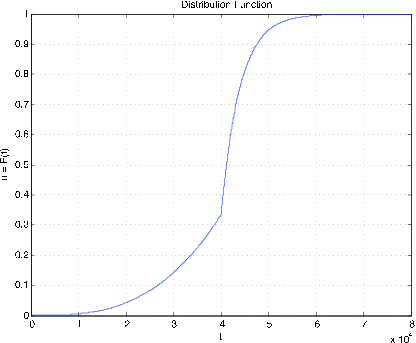
Малюнок 7.2.13. Функція розподілу для Приклад 7.2.12.

Приклад$\PageIndex{12}$: Radial tire mileage

Термін служби (в милі) певної марки радіальних шин може бути представлений випадковою величиною$X$ з щільністю

$f_X(t) = \begin{cases} t^2/a^3 & \text{for}\ \ 0 \le t < a \\ (b/a) e^{-k(t-a)} \text{for}\ \ a \le t \end{cases}$

де$a = 40,000$,$b = 20/3$, і$k = 1/4000$. Визначте$P(X \ge 45,000$.

>> a = 40000;
>> b = 20/3;
>> k = 1/4000;
>> % Test shows cutoff point of 80000 should be satisfactory
>> tappr
Enter matrix [a b] of x-range endpoints  [0 80000]
Enter number of x approximation points  80000/20
Enter density as a function of t  (t.^2/a^3).*(t < 40000) + ...
(b/a)*exp(k*(a-t)).*(t >= 40000)
Use row matrices X and PX as in the simple case
>> P = (X >= 45000)*PX'
P   =  0.1910             % Theoretical value = (2/3)exp(-5/4) = 0.191003
>> cdbn
Enter row matrix of VALUES  X
Enter row matrix of PROBABILITIES  PX  % See Figure 7.2.14 for plot

В даному випадку ми використовуємо досить велику кількість точок наближення. Як наслідок, результати виходять досить точними. У випадку з однією змінною позначення великої кількості апроксимуючих точок зазвичай не викликає проблем з пам'яттю комп'ютера.

Загальна процедура наближення

Тепер ми покажемо, що будь-яка обмежена дійсна випадкова величина може бути наближена так близько, як потрібно, простою випадковою величиною (тобто такою, що має скінченний набір можливих значень). Для необмеженого випадку наближення є близьким, за винятком частини діапазону, що має довільно малу загальну ймовірність.

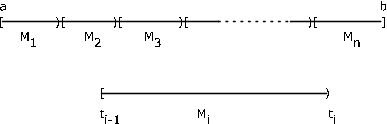
Обмежуємо наше обговорення обмеженим випадком, в якому діапазон$X$ обмежений інтервалом$I = [a, b]$. Припустимо,$I$ розділений на$n$ підінтервали точками$t_i$$1 \le i \le n - 1$, з$a = t_0$ і$b = t_n$. $M_i = [t_{i- 1}, t_i)$Дозволяти буде$i$ й підінтервал,$1 \le i \le n - 1$ і$M_n = [t_{n - 1}, t_n]$ (див. Рис. 7.14). Тепер випадкова величина$X$ може відображатися в будь-якій точці інтервалу, а отже, і в будь-яку точку в кожному підінтервалі$M_i$. $E_i X^{-1} (M_i)$Дозволяти бути безліч точок, відображених в$M_i$ по$X$. Потім$E_i$ формують перегородку з основного простору$\Omega$. Для даного підрозділу формуємо просту випадкову величину$X_s$ наступним чином. У кожному субінтервалі виберіть точку$s_i$,$t_{i - 1} \le s_i \le t_i$. Розглянемо просту випадкову величину$X_s = \sum_{i = 1}^{n} s_i I_{E_i}$.

Малюнок 7.2.14. Розділ інтервалу,$I$ включаючи діапазон$X$

Малюнок 7.2.15. Доопрацювання перегородки додатковими точками поділу.

Ця випадкова величина знаходиться в канонічній формі. Якщо$\omega \in E_i$, то$X(\omega) \in M_i$ і$X_s (\omega) = s_i$. Тепер абсолютне значення різниці задовольняє

$|X(\omega) - X_s (\omega)| < t_i - t_{i - 1}$довжина субінтервалу$M_i$

Оскільки це справедливо для кожного$\omega$ і відповідного субінтервалу, у нас є важливий факт

$|X(\omega) - X_s (\omega)|<$максимальна довжина$M_i$

Зробивши підінтервали досить малими, збільшивши кількість точок поділу, ми можемо зробити різницю настільки маленькою, наскільки нам заманеться.

У той час як вибір$s_i$ довільний у кожному$M_i$, вибір$s_i = t_{i - 1}$ (ліва кінцева точка) призводить до властивості$X_s(\omega) \le X(\omega) \forall \omega$. У цьому випадку, якщо ми додамо точки поділу, щоб зменшити розмір деяких або всіх$M_i$, нове просте наближення$Y_s$ задовольняє

$X_s(\omega) = Y_s(\omega) \le X(\omega)$$\forall \omega$

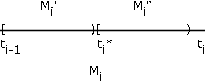
Щоб переконатися в цьому, розглянемо$t_i^{*} \in M_i$ (див. Рис. $M_i$розділений на розділи$M_i^{'} \bigcup M_i^{''}$ і$E_i$ розділяється на$E_i^{'} \bigcup E_i^{''}$. $X$карти$E_i^{'}$ в$M_i^{'}$ і$E_i^{''}$ в$M_i^{''}$. $Y_s$карти$E_i^{'}$ в$t_i$ і карти$E_i^{''}$$t_i^{''}$ в> t_i\). $X_s$карти як, так$E_i^{'}$ і$E_i^{''}$ в$t_i$. Таким чином, стверджувана нерівність повинна триматися для кожного$\omega$ Беручи послідовність розділів, в яких кожен наступний розділ уточнює попередній (тобто додає точки поділу) таким чином, що максимальна довжина підінтервалу йде до нуля, ми можемо сформувати незменшувану послідовність простих випадкових величин $X_n$які збільшуються$X$ для кожного$\omega$.

Останній результат може бути поширений на випадкові величини, необмежені вище. Просто дозвольте$N$ множині точок підрозділу поширюватися від$a$ до$N$, зробивши останній підінтервал$[N, \infty)$. Субінтервали від$a$ до$N$ робляться все коротше. Результатом є неспадна$\{X_N: 1 \le N\}$ послідовність простих випадкових величин, з$X_N(\omega) \to X(\omega)$ as$N \to \infty$, для кожної$\omega \in \Omega$.

Для обчислень ймовірності ми просто вибираємо інтервал, досить$I$ великий, щоб ймовірність зовні$I$ була незначною, і використовуємо просте наближення$I$.