1.2: Функції

\(\newcommand{\R}{\mathbb{R}}\)\(\newcommand{\N}{\mathbb{N}}\)\(\newcommand{\Z}{\mathbb{Z}}\)\(\newcommand{\Q}{\mathbb{Q}}\)\(\newcommand{\bs}{\boldsymbol}\)\(\newcommand{\range}{\text{range}}\)

Функції відіграють центральну роль у ймовірності та статистиці, як це роблять у кожній іншій галузі математики. Здебільшого докази в цьому розділі прості, тому обов'язково спробуйте їх самостійно, перш ніж читати ті, що знаходяться в тексті.

Визначення та властивості

Основні визначення

Почнемо з формального, технічного визначення функції. Це не дуже інтуїтивно, але має ту перевагу, що вимагає лише теорії множин.

Функція\(f\) з\(S\) множини в множину\(T\) є\(S \times T\) підмножиною набору продукту з властивістю\(x \in S\), що для кожного елемента існує унікальний елемент\(y \in T\) такий, що\((x, y) \in f\). Якщо\(f\) є функцією від\(S\) до\(T\) ми пишемо\(f: S \to T\). Якщо\((x, y) \in f\) ми пишемо\(y = f(x)\).

Менш формально функція\(f\) frm\(S\)\(T\) into - це правило (або процедура або алгоритм), яке присвоює кожному\(x \in S\) унікальний елемент\(f(x) \in T\). Визначення функції як множини впорядкованих пар, обумовлено Казимеж Куратовський. Термін карта або відображення також використовується замість функції, так що ми могли б сказати, що\(f\) карти\(S\) в\(T\).

Малюнок\(\PageIndex{1}\): Функція\( f\) з\( S \) в\( T \)

\(S\)Безліч і\(T\) у визначенні явно важливі.

Припустимо, що\(f: S \to T\).

1. Набір\(S\) є доменом\(f\).
2. Набір\(T\) є діапазоном або спільним доменом\(f\).
3. Діапазон of\(f\) - це набір значень функцій. Тобто,\(\range\left(f\right) = \left\{y \in T: y = f(x) \text{ for some } x \in S\right\}\).

Домен і діапазон повністю задаються функцією. Це не відповідає дійсності спільного домену: якщо\(f\) є функцією з\(S\) в\(T\), і\(U\) інший набір з\(T \subseteq U\), то ми також можемо думати про функції з\(S\) в\(U\).\(f\) Наступні визначення є природними і важливими.

Припустимо ще раз, що\(f: S \to T\).

1. \(f\)карти\(S\) на\(T\) якщо\(\range\left(f\right) = T\). Тобто для кожного\(y \in T\) існує\(x \in S\) таке, що\(f(x) = y\).
2. \(f\)один до одного, якщо окремі елементи в області зіставляються з різними елементами в діапазоні. Тобто, якщо\( u, \, v \in S \) і\( u \ne v \) тоді\( f(u) \ne f(v) \).

Зрозуміло, що функція завжди відображає свій домен на його діапазон. Зверніть увагу також, що\(f\) це один до одного, якщо\( f(u) = f(v) \) має\( u = v \) на увазі для\(u, \, v \in S\).

обернені функції

Функція, яка є один-на-один і на, може бути скасована в певному сенсі.

Якщо\(f\)\(S\) відображає один до одного на\(T\), обернене\(f\) є функцією\(f^{-1}\) з\(T\) на\(S\) задану\[ f^{-1}(y) = x \iff f(x) = y; \quad x \in S, \; y \in T \]

Якщо ви любите думати про функцію як набір впорядкованих пар, то\(f^{-1} = \{(y, x) \in T \times S: (x, y) \in f\}\). Той факт,\(f\) що один до одного і на гарантує, що\(f^{-1}\) це\(T\) дійсна функція від до\(S\). Встановлює\(S\) і\(T\) перебувають у відповідності один до одного, якщо існує функція один до одного з\(S\) onto\(T\). Один-на-один листування відіграє істотну роль у вивченні кардинальності.

Обмеження

Домен функції може бути обмежений для створення нової функції.

Припустимо, що\(f: S \to T\) і те\(A \subseteq S\). Функція,\(f_A: A \to T\)\( x \in A \) визначена\(f_A(x) = f(x)\) for, є обмеженням\(f\) to\(A\).

Як набір впорядкованих пар, зверніть увагу, що\(f_A = \{(x, y) \in f: x \in A\}\).

Склад

Композиція - це, мабуть, найважливіший спосіб об'єднання двох функцій для створення іншої функції.

Припустимо, що\(g: R \to S\) і\(f: S \to T\). Склад\(f\) з\(g\) - це функція,\(f \circ g: R \to T\) визначена\[ \left(f \circ g\right)(x) = f\left(g(x)\right), \quad x \in R \]

Склад асоціативний:

Припустимо\(h: R \to S\), що\(g: S \to T\), і\(f: T \to U\). Тоді\[ f \circ \left(g \circ h\right) = \left(f \circ g\right) \circ h \]

Доказ

Зверніть увагу, що обидві функції\( R \) відображаються в\( U \). Використовуючи визначення композиції, значення обох функцій при\( x \in R \) є\( f\left(g\left(h(x)\right)\right) \).

Таким чином ми можемо писати\(f \circ g \circ h\) без двозначності. З іншого боку, композиція не комутативна. Дійсно, залежно від доменів та спідоменів,\( f \circ g \) може бути визначено, коли\( g \circ f \) це не так. Навіть коли обидва визначені, вони можуть мати різні домени та спідомени, і тому, звичайно, не може бути однаковою функцією. Навіть коли обидва визначені і мають однакові домени та спідомени, ці дві композиції взагалі не будуть однаковими. Приклади всіх цих випадків наведені в обчислювальних вправах нижче.

Припустимо, що\(g: R \to S\) і\(f: S \to T\).

1. Якщо\(f\) і\(g\) є один до одного\(f \circ g\), то один до одного.
2. Якщо\(f\) і\(g\) знаходяться на то\(f \circ g\) знаходиться на.

Доказ

1. Припустимо, що\( u, \, v \in R \) і\( (f \circ g)(u) = (f \circ g)(v) \). Потім\( f\left(g(u)\right) = f\left(g(v)\right) \). Так як\( f \) один до одного,\( g(u) = g(v) \). Так як\( g \) один до одного,\( u = v \).
2. Припустимо, що\( z \in T \). Так як\( f \) є на, існують\( y \in S \) с\( f(y) = z \). Так як\( g \) є на, існує\( x \in R \) с\( g(x) = y \). Потім\( (f \circ g)(x) = f\left(g(x)\right) = f(y) = z \).

Функція ідентичності на множині\(S\) - це функція\(I_S\) від до\(S\),\(S\) визначена\(I_S(x) = x\) for\(x \in S\)

Функція ідентичності діє як ідентичність щодо дії композиції.

Якщо\(f: S \to T\) тоді

1. \(f \circ I_S = f\)
2. \(I_T \circ f = f\)

Доказ

1. Зауважте, що\( f \circ I_S: S \to T \). Для\( x \in S \),\( (f \circ I_S)(x) = f\left(I_S(x)\right) = f(x) \).
2. Зауважте, що\( I_T \circ f: S \to T \). Для\( x \in S \),\( (I_T \circ f)(x) = I_T\left(f(x)\right) = f(x) \).

Зворотна функція дійсно зворотна по відношенню до композиції.

Припустимо, що\(f\) це функція один до одного з\(S\) onto\(T\). Тоді

1. \(f^{-1} \circ f = I_S\)
2. \(f \circ f^{-1} = I_T\)

Доказ

1. Зауважте, що\( f^{-1} \circ f : S \to S \). Для\( x \in S \),\( \left(f^{-1} \circ f\right)(x) = f^{-1}\left(f(x)\right) = x \).
2. Зауважте, що\( f \circ f^{-1}: T \to T \). Для\( y \in T \),\(\left(f \circ f^{-1}\right)(y) = f\left(f^{-1}(y)\right) = y \)

Елемент\(x \in S^n\) можна розглядати як функцію з\(\{1, 2, \ldots, n\}\) в\(S\). Аналогічно, елемент\(x \in S^\infty\) може розглядатися як функція з\(\N_+\) в\(S\). Для такої послідовності\(x\), звичайно, ми зазвичай пишемо\(x_i\) замість\(x(i)\). Більш загально, якщо\(S\) і\(T\) є множинами, то множина всіх функцій from\(S\)\(T\) into позначається символом\(T^S\). Зокрема, як ми відзначали в останньому розділі,\( S^\infty \) також (і точніше) пишеться як\( S^{\N_+} \).

Припустимо, що\(g\) це функція один-на-один з\(R\) на,\(S\) і\(f\) це функція один до одного з\(S\) на\(T\). Потім\(\left(f \circ g\right)^{-1} = g^{-1} \circ f^{-1}\).

Доказ

Зверніть увагу, що\( (f \circ g)^{-1}: T \to R \) і\( g^{-1} \circ f^{-1}: T \to R \). Бо\( y \in T \), нехай\(x = \left(f \circ g\right)^{-1}(y) \). Потім\( \left(f \circ g\right)(x) = y \) так, що\( f\left(g(x)\right) = y \) і звідси\( g(x) = f^{-1}(y) \) і нарешті\( x = g^{-1}\left(f^{-1}(y)\right) \).

Зворотні зображення

Обернені зображення функції відіграють фундаментальну роль у ймовірності, особливо в контексті випадкових величин.

Припустимо, що\(f: S \to T\). Якщо\(A \subseteq T\), обернене зображення\(A\) under\(f\) є підмножиною\(S\) заданого\[f^{-1}(A) = \{x \in S: f(x) \in A\}\]

Так і\(f^{-1}(A)\) підмножина,\(S\) що складається з тих елементів, які відображаються в\(A\).

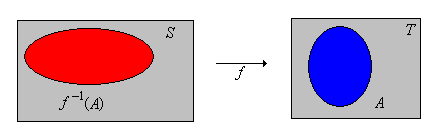
Малюнок\(\PageIndex{2}\): Обернене зображення\( A \) під\( f \)

Технічно, обернені зображення визначають нову функцію від\(\mathscr{P}(T)\) into\(\mathscr{P}(S)\). Ми використовуємо ті ж самі позначення, що і для зворотної функції, яка визначається, коли\(f\) один до одного і onto. Це дуже різні функції, але зазвичай не призводить до плутанини. Наступна важлива теорема показує, що обернені зображення зберігають усі операції множини.

Припустимо\(f: S \to T\), що, і що\(A, \, B \subseteq T\). Тоді

1. \(f^{-1}(A \cup B) = f^{-1}(A) \cup f^{-1}(B)\)
2. \(f^{-1}(A \cap B) = f^{-1}(A) \cap f^{-1}(B)\)
3. \(f^{-1}(A \setminus B) = f^{-1}(A) \setminus f^{-1}(B)\)
4. Якщо\(A \subseteq B\) тоді\(f^{-1}(A) \subseteq f^{-1}(B)\)
5. Якщо\(A\) і\(B\) розмежовуються, так\(f^{-1}(A)\) і є і\(f^{-1}(B)\)

Доказ

1. \( x \in f^{-1}(A \cup B) \)якщо і тільки тоді\( f(x) \in A \cup B \), коли і тільки якщо\( f(x) \in A \) або\( f(x) \in B \) якщо і тільки якщо\(x \in f^{-1}(A)\) або\( x \in f^{-1}(B) \) якщо і тільки якщо\( x \in f^{-1}(A) \cup f^{-1}(B) \)
2. Доказ такий же, як (а), з перетином, що замінює союз і з і заміною або по всьому.
3. Доказ такий же, як (а), з встановленою різницею, що замінює союз і з, а не замінює або по всьому.
4. Припустимо\( A \subseteq B \). Якщо\( x \in f^{-1}(A) \) то\( f(x) \in A \) і значить\( f(x) \in B \), так\( x \in f^{-1}(B) \).
5. Якщо\( A \) і\( B \) нероз'єднані, то з (б),\( f^{-1}(A) \cap f^{-1}(B) = f^{-1}(A \cap B) = f^{-1}(\emptyset) = \emptyset \).

Результат у частині (a) тримає для довільних об'єднань, а результат у частині (b) тримає для довільних перетинів. Ніяких нових ідей не задіяно, лише позначення складніше.

Припустимо, що\( \{A_i: i \in I\} \) це колекція підмножин\( T \), де\( I \) є непорожній набір індексів. Тоді

1. \( f^{-1}\left(\bigcup_{i \in I} A_i\right) = \bigcup_{i \in I} f^{-1}(A_i) \)
2. \( f^{-1}\left(\bigcap_{i \in I} A_i\right) = \bigcap_{i \in I} f^{-1}(A_i) \)

Доказ

1. \(x \in f^{-1}\left(\bigcup_{i \in I} A_i\right) \)якщо і тільки\( f(x) \in \bigcup_{i \in I} A_i \) якщо і тільки якщо\( f(x) \in A_i \) для деяких,\( i \in I \) якщо і тільки якщо\( x \in f^{-1}(A_i) \) для деяких,\( i \in I \) якщо і тільки якщо\(x \in \bigcup_{i \in I} f^{-1}(A_i) \)
2. Доказ такий же, як (а), з перетином, що замінює союз і з для кожної заміни для деяких.

Переслати зображення

Форвардні зображення функції є природним доповненням до зворотних зображень.

Припустимо ще раз, що\(f: S \to T\). Якщо\(A \subseteq S\), пряме зображення\(A\) under\(f\) є підмножиною\(T\) заданої\[ f(A) = \left\{f(x): x \in A\right\} \]

Так\(f(A)\) і діапазон\(f\) обмежений\(A\).

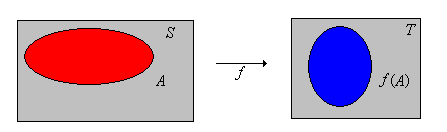
Малюнок\(\PageIndex{3}\): Форвардне зображення\( A \) під\( f \)

Технічно, форвардні зображення визначають нову функцію з\(\mathscr{P}(S)\) в\(\mathscr{P}(T)\), але ми використовуємо той самий символ\(f\) для цієї нової функції, що і для базової функції з\(S\) в\(T\) що ми почали з. Знову ж таки, дві функції дуже різні, але зазвичай не призводить до плутанини.

Може здатися, що форвардні зображення є більш природними, ніж зворотні зображення, але насправді зворотні зображення набагато важливіші, ніж форвардні (принаймні, в теорії ймовірності та вимірювання). На щастя, зворотні зображення також приємніші - на відміну від зворотних зображень, форвардні зображення не зберігають усіх встановлених операцій.

Припустимо\(f: S \to T\), що, і що\(A, \, B \subseteq S\). Тоді

1. \(f(A \cup B) = f(A) \cup f(B)\).
2. \(f(A \cap B) \subseteq f(A) \cap f(B)\). Рівність\( f \) тримається, якщо один до одного.
3. \(f(A) \setminus f(B) \subseteq f(A \setminus B)\). Рівність\( f \) тримається, якщо один до одного.
4. Якщо\(A \subseteq B\) тоді\(f(A) \subseteq f(B)\).

Доказ

1. Припустимо\( y \in f(A \cup B) \). Тоді\( y = f(x) \) для деяких\( x \in A \cup B \). Якщо\( x \in A \) то\( y \in f(A) \) і якщо\( x \in B \) тоді\( y \in f(B) \). В обох випадках\( y \in f(A) \cup f(B) \). І навпаки припустимо\( y \in f(A) \cup f(B) \). Якщо\( y \in f(A) \) то\( y = f(x) \) для деяких\( x \in A \). Але потім\( x \in A \cup B \) так\( y \in f(A \cup B) \). Аналогічно, якщо\( y \in f(B) \) то\( y = f(x) \) для деяких\( x \in B \). Але потім\( x \in A \cup B \) так\( y \in f(A \cup B) \).
2. Якщо\( y \in f(A \cap B) \) то\( y = f(x) \) для деяких\( x \in A \cap B \). Але потім\( x \in A \) так\( y \in f(A) \) і\( x \in B \) так\( y \in f(B) \) і звідси\( y \in f(A) \cap f(B) \). І навпаки, припустимо, що\( y \in f(A) \cap f(B) \). Тоді\( y \in f(A) \) і\( y \in f(B) \), так існує\( x \in A \) з\( f(x) = y \) і існує\( u \in B \) с\( f(u) = y\). На цьому етапі ми не можемо йти далі. Але якщо\( f \) один-на-один, то\( u = x \) і значить\( x \in A \) і\( x \in B \). Таким чином\( x \in A \cap B \) так\( y \in f(A \cap B) \).
3. Припустимо\( y \in f(A) \setminus f(B) \). Потім\( y \in f(A) \) і\( y \notin f(B) \). Отже\( y = f(x) \), для деяких\( x \in A \) і\( y \ne f(u) \) для кожного\( u \in B \). Таким чином,\( x \notin B \) так\( x \in A \setminus B \) і звідси\( y \in f(A \setminus B) \). І навпаки, припустимо\( y \in f(A \setminus B) \). Тоді\( y = f(x) \) для деяких\( x \in A \setminus B \). Звідси\( x \in A \) і так\( y \in f(A) \). Знову ж таки, доказ ламається на цьому етапі. Однак якщо\( f \) один-на-один і\( f(u) = y \) для деяких\( u \in B \), то\( u = x \) так\( x \in B \), протиріччя. Звідси\( f(u) \ne y \) для кожного\( u \in B \) так\( y \notin f(B) \). Таким чином\( y \in f(A \setminus B) \).
4. Припустимо\( A \subseteq B \). Якщо\( y \in f(A) \) то\( y = f(x) \) для деяких\( x \in A \). Але потім\( x \in B \) так\( y \in f(B) \).

Результат у частині (а) утримують для довільних об'єднань, а результати в частині (b) утримують для довільних перетинів. Ніяких нових ідей не задіяно, лише позначення складніше.

Припустимо, що\( \{A_i: i \in I\} \) це колекція підмножин\( S \), де\( I \) є непорожній набір індексів. Тоді

1. \( f\left(\bigcup_{i \in I} A_i\right) = \bigcup_{i \in I} f(A_i) \).
2. \( f\left(\bigcap_{i \in I} A_i\right) \subseteq \bigcap_{i \in I} f(A_i) \). Рівність\( f \) тримається, якщо один до одного.

Доказ

1. \( y \in f\left(\bigcup_{i \in I} A_i\right)\)якщо і тільки якщо\( y = f(x) \) для деяких,\( x \in \bigcup_{i \in I} A_i \) якщо і тільки якщо\( y = f(x) \) для деяких\( x \in A_i \) і деяких,\( i \in I \) якщо і тільки якщо\( y \in f(A_i) \) для деяких,\( i \in I \) якщо і тільки якщо\(y \in \bigcup_{i \in I} f(A_i)\).
2. Якщо\( y \in f\left(\bigcap_{i \in I} A_i\right) \) то\( y = f(x) \) для деяких\( x \in \bigcap_{i \in I} A_i \). Отже,\( x \in A_i \) для кожного\( i \in I \) так\( y \in f(A_i) \) для кожного\( i \in I \) і таким чином\( y \in \bigcap_{i \in I} f(A_i) \). І навпаки, припустимо, що\( y \in \bigcap_{i \in I} f(A_i) \). Тоді\( y \in f(A_i) \) для кожного\( i \in I \). Отже, для кожного\( i \in I \) існує\( x_i \in A_i \) с\( y = f(x_i) \). \( f \)Це один до одного,\( x_i = x_j \) для всіх\( i, \, j \in I \). Викликати загальне значення\( x \). Тоді\( x \in A_i \) для кожного\( i \in I \) так\( x \in \bigcap_{i \in I} A_i \) і тому\( y \in f\left(\bigcap_{i \in I} A_i\right) \).

Припустимо ще раз, що\(f: S \to T\). Як зазначалося раніше, форвардні зображення\(f\) визначають функцію від\(\mathscr{P}(S)\)\(\mathscr{P}(T)\) into, а зворотні зображення визначають функцію від\(\mathscr{P}(T)\) into\(\mathscr{P}(S)\). Можна сподіватися, що ці функції є зворотними один від одного, але на жаль немає.

Припустимо, що\(f: S \to T\).

1. \(A \subseteq f^{-1}\left[f(A)\right]\)для\(A \subseteq S\). Рівність\( f \) тримається, якщо один до одного.
2. \(f\left[f^{-1}(B)\right] \subseteq B\)для\(B \subseteq T\). Рівність\( f \) тримається, якщо на.

Доказ

1. Якщо\( x \in A \) то\( f(x) \in f(A) \) і звідси\( x \in f^{-1}\left[f(A)\right] \). І навпаки, припустимо, що\( x \in f^{-1}\left[f(A)\right] \). Тоді\( f(x) \in f(A) \) так\( f(x) = f(u) \) для деяких\( u \in A \). На цьому етапі ми не можемо йти далі. Але якщо\( f \) один до одного, то\( u = x \) і значить\( x \in A \).
2. Припустимо\( y \in f\left[f^{-1}(B)\right] \). Тоді\( y = f(x) \) для деяких\( x \in f^{-1}(B) \). Але потім\( y = f(x) \in B \). І навпаки, припустимо, що\( f \) знаходиться на і\( y \in B \). Існують\( x \in S \) с\( f(x) = y \). Звідси\( x \in f^{-1}(B) \) і так\( y \in f\left[f^{-1}(B)\right] \).

Простіри дійсних функцій

Особливе значення мають\(S\) дійсні функції на заданій множині. Звичайні арифметичні операції над такими функціями визначаються точково.

Припустимо\( c \in \R \), що\( f, \, g: S \to \R \) і, то\( f + g, \, f - g, \, f g, \, c f, \, f / g: S \to \R\) визначаються наступним чином для всіх\( x \in S \).

1. \( (f + g)(x) = f(x) + g(x) \)
2. \( (f - g)(x) = f(x) - g(x) \)
3. \( (f g)(x) = f(x) g(x) \)
4. \( (c f)(x) = c f(x) \)
5. \((f/g)(x) = f(x) / g(x)\)припускаючи, що\(g(x) \ne 0\) для\(x \in S\).

Тепер давайте\(\mathscr V\) позначимо колекцію всіх функцій з заданого множини\(S\) в\(\R\). Факт, який дуже важливий за ймовірністю, як і інші галузі аналізу, полягає в тому\( \mathscr V \), що при додаванні та скалярному множенні, як визначено вище, є векторним простором. Нульова функція\( \bs 0 \) визначається, звичайно ж,\( \bs{0}(x) = 0 \) для всіх\( x \in S \).

\( (\mathscr V, +, \cdot) \)це векторний простір над\( \R \). Тобто для всіх\( f, \, g, \, h \in \mathscr V \) і\( a, \, b \in \R \)

1. \( f + g = g + f \), Комутативна властивість векторного додавання.
2. \( f + (g + h) = (f + g) + h \), Асоціативна властивість векторного додавання.
3. \( a(f + g) = a f + a g \), скалярне множення розподіляється по векторному додаванню.
4. \( (a + b)f = a f + b f \), скалярне множення розподільне над скалярним додаванням.
5. \( f + \bs 0 = f\), Існування нульового вектора.
6. \( f + (-f) = \bs 0 \), Існування адитивних інверсів.
7. \( 1 \cdot f = f \), властивість єдності.

Доказ

Кожне з цих властивостей випливає з відповідної властивості в\( \R \).

Різні підпростори також\( \mathscr V \) важливі за ймовірністю. Ми повернемося до обговорення векторних просторів функцій в розділах про часткові порядки і в розширених розділах про метричні простори і теорії мір.

Функції індикатора

Для нашого наступного обговорення, припустимо, що\(S\) це універсальна множина, так що всі інші згадані множини є підмножинами\(S\).

Припустимо, що\(A \subseteq S\). Індикаторною функцією\(A\) є функція,\(\bs{1}_A: S \to \{0, 1\}\) визначена наступним чином:\[ \bs{1}_A(x) = \begin{cases} 1, & x \in A \\ 0, & x \notin A \end{cases} \]

Таким чином, індикаторна функція\( A \) просто вказує,\( x \in A \) для кожного чи ні\( x \in S \). І навпаки, будь-яка функція на\(S\) що просто приймає значення 0 і 1 є індикаторною функцією.

Якщо\(f: S \to \{0, 1\}\)\(f\) то індикаторна функція набору\(A = f^{-1}\{1\} = \{x \in S: f(x) = 1\}\).

Таким чином, існує відповідність один до одного між\(\mathscr{P}(S)\), набором потужності та\(S\) сукупністю індикаторних функцій\(\{0, 1\}^S\). Наступний результат показує, як алгебра множин відповідає арифметичній алгебрі індикаторних функцій.

Припустимо, що\(A, \, B \subseteq S\). Тоді

1. \(\bs{1}_{A \cap B} = \bs{1}_A \, \bs{1}_B = \min\left\{\bs{1}_A, \bs{1}_B\right\}\)
2. \(\bs{1}_{A \cup B} = 1 - \left(1 - \bs{1}_A\right)\left(1 - \bs{1}_B\right) = \max\left\{\bs{1}_A, \bs{1}_B\right\}\)
3. \(\bs{1}_{A^c} = 1 - \bs{1}_A\)
4. \(\bs{1}_{A \setminus B} = \bs{1}_A \left(1 - \bs{1}_B\right)\)
5. \(A \subseteq B\)якщо і тільки якщо\(\bs{1}_A \le \bs{1}_B\)

Доказ

1. Зверніть увагу, що обидві функції праворуч просто приймають значення 0 і 1. Причому,\( \bs{1}_A(x) \bs{1}_B(x) = \min\left\{\bs{1}_A(x), \bs{1}_B(x)\right\} = 1\) якщо і тільки якщо\( x \in A \) і\( x \in B \).
2. Зверніть увагу, що обидві функції праворуч просто приймають значення 0 і 1. Причому,\( 1 - \left(1 - \bs{1}_A(x)\right)\left(1 - \bs{1}_B(x)\right) = \max\left\{\bs{1}_A(x), \bs{1}_B(x)\right\} = 1 \) якщо і тільки якщо\( x \in A \) або\( x \in B \).
3. Зверніть увагу, що\( 1 - \bs{1}_A \) просто приймає значення 0 і 1. Причому,\( 1 - \bs{1}_A(x) = 1\) якщо і тільки якщо\( x \notin A \).
4. Зверніть увагу, що\( \bs{1}_{A \setminus B} = \bs{1}_{A \cap B^c} = \bs{1}_A \bs{1}_{B^c} = \bs{1}_A \left(1 - \bs{1}_B\right) \) по частинам (а) і (с).
5. Оскільки обидві функції просто приймають значення 0 і 1, зверніть увагу, що\( \bs{1}_A \le \bs{1}_B \) якщо і тільки якщо\( \bs{1}_A(x) = 1 \) має на увазі\( \bs{1}_B(x) = 1 \). Але в свою чергу, це рівнозначно\( A \subseteq B \).

Результати в частині (а) поширюються на довільні перетину, а результати в частині (b) поширюються на довільні союзи.

Припустимо, що\( \{A_i: i \in I\} \) це колекція підмножин\( S \), де\( I \) є непорожній набір індексів. Тоді

1. \( \bs{1}_{\bigcap_{i \in I} A_i} = \prod_{i \in I} \bs{1}_{A_i} = \min\left\{\bs{1}_{A_i}: i \in I\right\} \)
2. \( \bs{1}_{\bigcup_{i \in I} A_i} = 1 - \prod_{i \in I}\left(1 - \bs{1}_{A_i}\right) = \max\left\{\bs{1}_{A_i}: i \in I\right\} \)

Доказ

Загалом, продукт над нескінченним набором індексу може не мати сенсу. Але якщо всі фактори або 0 або 1, як вони тут, то ми можемо просто визначити продукт бути 1, якщо всі фактори 1, і 0 в іншому випадку.

1. Функції посередині і праворуч просто приймають значення 0 і 1. Більш того, обидва приймають значення 1 при\( x \in S \) if і тільки якщо\( x \in A_i \) для кожного\( i \in I \).
2. Функції посередині і праворуч просто приймають значення 0 і 1. Причому обидва приймають значення 1 при\( x \in S \) if і тільки якщо\( x \in A_i \) для деяких\( i \in I \).

Мультимножини

Мультимножина схожа на звичайний набір, за винятком того, що елементи можуть повторюватися. \( A \)Мультимножина (з елементами з універсальної множини\( S \)) може бути однозначно пов'язана з його функцією кратності\( m_A: S \to \N \), де\( m_A(x) \) кількість разів, що елемент\( x \) знаходиться в\( A \) для кожного\( x \in S \). Таким чином, множинність функція мультимножини відіграє ту ж роль, що функція індикатора робить для звичайної множини. Мультимножини виникають природно, коли об'єкти відбираються з заміною (але без урахування порядку) від сукупності. Різні моделі вибірки досліджуються в розділі про комбінаторні структури. Ми не будемо вдаватися в подробиці про операції над мультимножинами, але визначення - це прості узагальнення тих, що для звичайних множин.

Припустимо, що\( A \) і\( B \) є мультимножинами з елементами з універсального набору\( S \). Тоді

1. \( A \subseteq B \)якщо і тільки якщо\( m_A \le m_B \)
2. \(m_{A \cup B} = \max\{m_A, m_B\}\)
3. \( m_{A \cap B} = \min\{m_A, m_B\} \)
4. \( m_{A + B} = m_A + m_B \)

Простір продукту

Використовуючи функції, ми можемо узагальнити декартові добутки, вивчені раніше. У цьому обговоренні ми припускаємо, що\(S_i\) це набір для кожного\(i\) в непорожньому наборі індексів\(I\).

Визначте товарний набір\[ \prod_{i \in I} S_i = \left\{x: x \text{ is a function from } I \text{ into } \bigcup_{i \in I} S_i \text{ such that } x(i) \in S_i \text{ for each } i \in I\right\} \]

Зауважте, що крім непорожнього, немає припущень щодо кардинальності набору індексів\( I \). Звичайно, якщо\( I = \{1, 2 \ldots, n\} \) для деяких\( n \in \N_+ \), або якщо\( I = \N_+ \) то ця конструкція зводиться до\( S_1 \times S_2 \times \cdots \times S_n \) і до\( S_1 \times S_2 \times \cdots \), відповідно. Оскільки ми хочемо зробити позначення більш схожим на позначення простих декартових добутків, ми будемо писати\( x_i \) замість\( x(i) \) значення функції\( x \) at\( i \in I \), і ми іноді посилаємося на це значення як\( i \) го координати\( x \). Нарешті, зверніть увагу, що якщо\( S_i = S \) для кожного\( i \in I \),\( \prod_{i \in I} S_i \) то просто набір всіх функцій from\( I \) into\( S \), який ми позначили\( S^I \) вище.

Для\( j \in I \) визначення проекції\( p_j: \prod_{i \in I} S_i \to S_j \) за допомогою\( p_j(x) = x_j \) for\( x \in \prod_{i \in I} S_i \).

Так\( p_j(x) \) це тільки\( j \) координата го\( x \). Проекції мають основне значення для виробничих просторів. Зокрема, ми маємо кращий спосіб розглядати проекції підмножини набору продуктів.

Для\( A \subseteq \prod_{i \in I} S_i \) і\( j \in I \), вперед зображення\( p_j(A) \) є проекцією\( A \) на\( S_j \).

Доказ

Зверніть увагу на те\( p_j(A) = \{p_j(x): x \in A\} = \{x_j: x \in A\} \), що\( j \) множина всіх координат точок в\( A \).

Отже, властивості проекції, які ми вивчали в останньому розділі, є лише окремими випадками властивостей зображень вперед. Проекції також дозволяють нам отримати координатні функції простим способом.

Припустимо, що\( R \) це набір, і що\( f: R \to \prod_{i \in I} S_i \). Якщо\( j \in I \) тоді\( p_j \circ f : R \to S_j \) є\( j \) координатною функцією\( f \).

Доказ

Зверніть увагу\( x \in R \), що\( (p_j \circ f)(x) = p_j[f(x)] = f_j(x) \) for,\( j \) -й координата\( f(x) \in \prod_{i \in I} S_i \).

Це буде виглядати більш звично для простого декартового продукту. Якщо\( f: R \to S_1 \times S_2 \times \cdots \times S_n \), то\( f = (f_1, f_2, \ldots, f_n) \) де\( f_j: R \to S_i \) - координатна функція для\( j \in \{1, 2, \ldots, n\} \).\( j \)

Поперечні перерізи підмножини множини добутку можуть бути виражені через обернені зображення функції. Для початку нам знадобляться деякі додаткові позначення. Припустимо, що наш набір індексів\( I \) має як мінімум два елементи. Для\( j \in I \) і\( u \in S_j \), визначте\( j_u : \prod_{i \in I - \{j\}} S_i \to \prod_{i \in I} S_i \),\( j_u (x) = y \) де\( y_i = x_i \) для\( i \in I - \{j\} \) і\( y_j = u \). У словах,\( j_u \) приймає точку\( x \in \prod_{i \in I - \{j\}} S_i \) і\( u \) призначає координату\( j \), щоб створити точку\( y \in \prod_{i \in I} S_i \).

У наведеній вище настройці\( j \in I \)\( u \in S_j \) if, а\( A \subseteq \prod_{i \in I} S_i \) потім\(j_u^{-1}(A)\) - це перетин\( A \) в\( j \) й координаті at\( u \).

Доказ

Це випливає з визначення поперечного перерізу:\( j_u^{-1}(A) \) це сукупність всіх\(x \in \prod_{i \in I - \{j\}} S_i \) таких, що\( y \) визначено вище, знаходиться в\( A \) і має\( j \) th координату\( u \).

Давайте розглянемо це для вироби з двох наборів\( S \) і\( T \). Для\( x \in S \), функція\( 1_x: T \to S \times T \) задається за допомогою\( 1_x(y) = (x, y) \). Аналогічно\( y \in T \), for, функція\( 2_y: S \to S \times T \) задається\( 2_y(x) = (x, y) \). Припустимо, що тепер\( A \subseteq S \times T \). Якщо\( x \in S \), то\( 1_x^{-1}(A) = \{y \in T: (x, y) \in A\} \), саме визначення перетину\( A \) в першій координаті в\( x \). Аналогічно\( y \in T \), якщо\( 2_y^{-1}(A) = \{x \in S: (x, y) \in A\} \), то, саме визначення перетину\( A \) в другій координаті в\( y \). Ця конструкція не особливо важлива, крім того, щоб показати, що поперечні перерізи є зворотними зображеннями. Таким чином, той факт, що поперечні перерізи зберігають всі множинні операції, є простим наслідком того, що обернені зображення взагалі зберігають множинні операції.

Оператори

Іноді функції мають спеціальні інтерпретації в певних налаштуваннях.

Припустимо, що\(S\) це набір.

1. Функцію іноді\(f: S \to S\) називають унарним оператором on\(S\).
2. Функцію іноді\(g: S \times S \to S\) називають двійковим оператором on\(S\).

Як випливає з назв, унарний оператор\(f\) працює над елементом\(x \in S\) для отримання нового елемента\(f(x) \in S\). Аналогічно, двійковий оператор\(g\) працює на парі елементів\((x, y) \in S \times S\) для отримання нового елемента\(g(x, y) \in S\). Арифметичні оператори є квінтесенціальними прикладами:

Нижче наведено оператори на\(\R\):

1. \(\text{minus}(x) = -x\)є унарним оператором.
2. \(\text{sum}(x, y) = x + y\)є двійковим оператором.
3. \(\text{product}(x, y) = x\,y\)є двійковим оператором.
4. \(\text{difference}(x, y) = x - y\)є двійковим оператором.

Для фіксованого універсального множини оператори множини\(S\), вивчені в розділі «Множини», надають інші приклади.

Для заданого\(S\) множини наступні оператори на\(\mathscr P(S)\):

1. \(\text{complement}(A) = A^c\)є унарним оператором.
2. \(\text{union}(A, B) = A \cup B\)є двійковим оператором.
3. \(\text{intersect}(A, B) = A \cap B\)є двійковим оператором.
4. \(\text{difference}(A, B) = A \setminus B\)є двійковим оператором.

Як ілюструють ці приклади, двійковий оператор часто пишеться як,\( x \, f \, y \) а не\( f(x, y) \). Все-таки корисно знати, що оператори - це просто функції спеціального типу.

Припустимо, що\(f\) це унарний оператор на множині\(S\),\(g\) це двійковий оператор on\(S\), і що\(A \subseteq S\).

1. \(A\)закривається під\(f\) якщо\(x \in A\) мається на увазі\(f(x) \in A\).
2. \(A\)закривається під\(g\) якщо\((x, y) \in A \times A\) мається на увазі\(g(x, y) \in A\).

Таким чином\(A\), якщо закривається під унарним оператором\(f\), то\(f\)\(A\) обмежується унарним оператором на\(A\). Similary\(A\) if закритий під двійковим оператором\(g\), то\(g\) обмежений\(A \times A\) - це бінарний оператор on\(A\). Повернемося до нашого найпростішого прикладу.

Для арифметичних операторів на\(\R\),

1. \(\N\)закривається під плюс і раз, але не під мінусом і різницею.
2. \(\Z\)закривається під плюсом, раз, мінус і різниця.
3. \( \Q \)закривається під плюсом, раз, мінус і різниця.

Багато властивостей, з якими ви знайомі для спеціальних операторів (таких як арифметичні та множинні оператори), тепер можна сформулювати загалом.

Припустимо, що\(f\) і\(g\) є бінарними операторами на множині\(S\). У наступних визначеннях,\(x\),\(y\), і\(z\) є довільними елементами\(S\).

1. \(f\)є комутативним\(f(x, y) = f(y, x)\), якщо, тобто,\( x \, f \, y = y \, f \, x \)
2. \(f\)асоціативний якщо\(f(x, f(y, z)) = f(f(x, y), z)\), тобто\( x \, f \, (y \, f \, z) = (x \, f \, y) \, f \, z \).
3. \(g\)розподіляє над\(f\) (зліва) якщо\(g(x, f(y, z)) = f(g(x, y), g(x, z))\), тобто\( x \, g \, (y \, f \, z) = (x \, g \, y) \, f \, (x \, g \, z) \)

Аксіома вибору

Припустимо, що\(\mathscr{S}\) це збірка непорожніх підмножин множини\(S\). Аксіома вибору стверджує, що існує функція\(f: \mathscr{S} \to S\) з властивістю, що\(f(A) \in A\) для кожного\(A \in \mathscr{S}\). Функція\(f\) відома як функція вибору.

Віддячена більшої частини математичного жаргону, ідея дуже проста. Оскільки кожен набір\(A \in \mathscr{S}\) непорожній, ми можемо вибрати елемент\(A\); ми будемо називати елемент, який ми вибираємо,\(f(A)\) і таким чином наші виділення визначають функцію. Насправді, ви можете задатися питанням, навіщо нам взагалі потрібна аксіома. Проблема полягає в тому, що ми не дали правила (або процедури або алгоритму) вибору елементів множин у збірці. Дійсно, ми можемо недостатньо знати про множини в колекції, щоб визначити конкретне правило, тому в такому випадку аксіома вибору просто гарантує існування функції вибору. Деякі математики, відомі як конструкціоністи, не сприймають аксіому вибору, і наполягають на чітко визначених правилах побудови функцій.

Приємним наслідком аксіоми вибору є тип подвійності між функціями один до одного і on-functions.

Припустимо, що\(f\) це функція від множини\(S\) до множини\(T\). Існує функція один до одного\(g\) з\(T\) into\(S\).

Доказ.

Для кожного\(y \in T\) набір\(f^{-1}\{y\}\) не порожній, так як\(f\) знаходиться на. За аксіомою вибору ми можемо вибрати елемент\(g(y)\) з\(f^{-1}\{y\}\) для кожного\(y \in T\). Отримана функція\(g\) - один до одного.

Припустимо, що\(f\) це функція один-на-один з множини\(S\) в множину\(T\). Існує функція\(g\) від\(T\) onto\(S\).

Доказ.

Закріпіть спеціальним елементом\(x_0 \in S\). Якщо\(y \in \text{range}(f)\), існує унікальний\(x \in S\) с\(f(x) = y\). Визначте\(g(y) = x\). Якщо\(y \notin \text{range}(f)\), визначте\(g(y) = x_0\). Функція\(g\) включена.

Обчислювальні вправи

Деякі елементарні функції

Кожне з наведених нижче правил визначає функцію from\(\R\) into\(\R\).

• \(f(x) = x^2\)
• \(g(x) = \sin(x)\)
• \(h(x) = \lfloor x \rfloor\)
• \(u(x) = \frac{e^x}{1 + e^x}\)

Знайдіть діапазон функції та визначте, чи є функція один-на-один у кожному з наступних випадків:

1. \(f\)
2. \(g\)
3. \(h\)
4. \(u\)

Відповідь

1. Діапазон\([0, \infty)\). Не один на один.
2. Діапазон\([-1, 1]\). Не один на один.
3. Діапазон\(\Z\). Не один на один.
4. Діапазон\((0, 1)\). Один до одного.

Знайдіть такі зворотні зображення:

1. \(f^{-1}[4, 9]\)
2. \(g^{-1}\{0\}\)
3. \(h^{-1}\{2, 3, 4\}\)

Відповідь

1. \([-3, -2] \cup [2, 3]\)
2. \(\{n \, \pi: n \in \Z\}\)
3. \([2, 5)\)

\(u\)Функція один-на-один. Знайти (тобто дати домен і правило для) зворотну функцію\(u^{-1}\).

Відповідь

\(u^{-1}(p) = \ln\left(\frac{p}{1-p}\right)\)для\(p \in (0, 1)\)

Дайте правило і знайдіть діапазон для кожної з наступних функцій:

1. \(f \circ g\)
2. \(g \circ f\)
3. \(h \circ g \circ f\)

Відповідь

1. \((f \circ g)(x) = \sin^2(x)\). Діапазон\([0, 1]\)
2. \((g \circ f)(x) = \sin\left(x^2\right)\). Діапазон\([-1, 1]\)
3. \((h \circ g \circ f)(x) = \lfloor \sin(x^2) \rfloor\). Діапазон\(\{-1, 0, 1\}\)

Зверніть увагу, що\( f \circ g \) і\( g \circ f \) є чітко визначеними функціями з\( \R \) в\( \R \), але\( f \circ g \ne g \circ f \).

Кубики

Нехай\(S = \{1, 2, 3, 4, 5, 6\}^2\). Це набір можливих результатів, коли кидається пара стандартних кубиків. Дозволяти\(f\)\(g\)\( u \),,, і\( v \) бути функції від\(S\) в\(\Z\) визначені наступними правилами:

• \(f(x, y) = x + y\)
• \( g(x, y) = y - x \)
• \(u(x, y) = \min\{x, y\}\)
• \(v(x, y) = \max\{x, y\}\)

Крім того, нехай\( F \) і\( U \) бути функції,\( F = (f, g) \) визначені і\( U = (u, v) \).

Знайдіть діапазон кожної з наступних функцій:

1. \(f\)
2. \( g \)
3. \(u\)
4. \(v\)
5. \(U\)

Відповідь

1. \(\{2, 3, 4, \ldots, 12\}\)
2. \( \{-5, -4, \ldots, 4, 5\} \)
3. \(\{1, 2, 3, 4, 5, 6\}\)
4. \(\{1, 2, 3, 4, 5, 6\}\)
5. \(\left\{(i, j) \in \{1, 2, 3, 4, 5, 6\}^2: i \le j\right\}\)

Надайте кожне з наступних обернених зображень у вигляді списку:

1. \(f^{-1}\{6\}\)
2. \(u^{-1}\{3\}\)
3. \(v^{-1}\{4\}\)
4. \(U^{-1}\{(3, 4)\}\)

Відповідь

1. \(\{(1,5), (2,4), (3,3), (4,2), (5,1)\}\)
2. \(\{(3,3), (3,4), (4,3), (3,5), (5,3), (3,6), (6,3)\}\)
3. \(\{(1,4), (4,1), (2,4), (4,2), (3,4), (4,3), (4,4)\}\)
4. \(\{(3,4), (4,3)\}\)

Знайдіть кожен з наступних складів:

1. \( f \circ U \)
2. \( g \circ U \)
3. \( u \circ F \)
4. \( v \circ F \)
5. \( F \circ U \)
6. \( U \circ F \)

Відповідь

1. \( f \circ U = f \)
2. \( g \circ U = \left|g\right| \)
3. \( u \circ F = g \)
4. \( v \circ F = f \)
5. \( F \circ U = \left(f, \left|g\right|\right) \)
6. \( U \circ F = (g, f) \)

Зверніть увагу,\( f \circ U \) що поки чітко визначена, не\( U \circ f \) є. Зауважте також, що\( f \circ U = f \) хоча\( U \) це не функція ідентичності на\( S \).

Бітові рядки

Нехай\( n \in \N_+ \) і нехай\( S = \{0, 1\}^n \) і\( T = \{0, 1, \ldots, n\} \). Нагадаємо, що елементи\( S \) є\( n \) бітовими рядками довжини\( n \), і можуть представляти можливі результати кидання монети (де 1 означає голови, а 0 означає хвости). \( f: S \to T \)Дозволяти бути функція, визначена\( f(x_1, x_2, \ldots, x_n) = \sum_{i=1}^n x_i \). Зверніть увагу, що\( f(\bs{x}) \) це лише кількість 1s у рядку бітів\( \bs{x} \). \( g: T \to S \)Дозволяти функція, визначена\( g(k) = \bs{x}_k \) де\( \bs{x}_k \) позначає бітовий рядок з\( k \) 1s, а потім\( n - k \) 0.

Знайдіть кожне з наведених нижче

1. \( f \circ g \)
2. \( g \circ f \)

Відповідь

1. \( f \circ g: T \to T \)і\( \left(f \circ g\right)(k) = k \).
2. \( g \circ f: S \to S \)і\( \left(g \circ f\right)(\bs{x}) = \bs{x}_k \) де\( k = f(\bs{x}) = \sum_{i=1}^n x_i \). У словах,\( \left(g \circ f\right)(\bs{x}) \) це бітовий рядок з такою ж кількістю 1s, що і\( \bs{x} \), але переставлений так, щоб всі 1s були першими.

У попередній\( g \circ f \) вправі зверніть увагу, що\( f \circ g \) і обидва чітко визначені, але мають різні домени, і тому, звичайно, не однакові. Зауважте також,\( f \circ g \) що функція ідентичності\( T \) включена, але не\( f \) є оберненою\( g \). Дійсно,\( f \) це не один-на-один, і тому не має зворотного. Однак\( f \) обмежений\( \left\{\bs{x}_k: k \in T\right\} \) (діапазон\( g \)) є один до одного і є зворотним\( g \).

Нехай\( n = 4 \). Дайте\( f^{-1}(\{k\}) \) в формі списку для кожного\( k \in T \).

Відповідь

1. \( f^{-1}(\{0\}) = \{0000\} \)
2. \( f^{-1}(\{1\}) = \{1000, 0100, 0010, 0001\} \)
3. \( f^{-1}(\{2\}) = \{1100, 1010, 1001, 0110, 0101, 0011\} \)
4. \( f^{-1}(\{3\}) = \{1110, 1101, 1011, 0111\} \)
5. \( f^{-1}(\{4\}) = \{1111\}\)

Знову нехай\( n = 4 \). Нехай\( A = \{1000, 1010\} \) і\( B = \{1000, 1100\} \). Надайте кожному з наступних пунктів у вигляді списку:

1. \( f(A) \)
2. \( f(B) \)
3. \( f(A \cap B) \)
4. \( f(A) \cap f(B) \)
5. \( f^{-1}\left(f(A)\right) \)

Відповідь

1. \( \{1, 2\} \)
2. \( \{1, 2\} \)
3. \( \{1\} \)
4. \( \{1, 2\} \)
5. \( \{1000, 0100, 0010, 0001, 1100, 1010, 1001, 0110, 0101, 0011\} \)

У попередній вправі зверніть увагу, що\( f(A \cap B) \subset f(A) \cap f(B) \) і\(A \subset f^{-1}\left(f(A)\right) \).

Функції індикатора

Припустимо, що\(A\) і\(B\) є підмножинами універсальної множини\(S\). Експрес, з точки зору\(\bs{1}_A\) і\(\bs{1}_B\), індикаторну функцію кожного з 14 нетривіальних множин, які можуть бути побудовані з\(A\) і\(B\). Використовуйте програму діаграми Венна, щоб допомогти.

Відповідь

1. \(\bs{1}_A \)
2. \(\bs{1}_B \)
3. \( \bs{1}_{A^c} = 1 - \bs{1}_A \)
4. \( \bs{1}_{B^c} = 1 - \bs{1}_B \)
5. \( \bs{1}_{A \cap B} = \bs{1}_A \bs{1}_B \)
6. \( \bs{1}_{A \cup B} = \bs{1}_A + \bs{1}_B - \bs{1}_A \bs{1}_B \)
7. \( \bs{1}_{A \cap B^c} = \bs{1}_A - \bs{1}_A \bs{1}_B \)
8. \( \bs{1}_{B \cap A^c} = \bs{1}_B - \bs{1}_A \bs{1}_B \)
9. \( \bs{1}_{A \cup B^c} = 1 - \bs{1}_B + \bs{1}_A \bs{1}_B \)
10. \( \bs{1}_{B \cup A^c} = 1 - \bs{1}_A + \bs{1}_A \bs{1}_B \)
11. \( \bs{1}_{A^c \cap B^c} = 1 - \bs{1}_A - \bs{1}_B + \bs{1}_A \bs{1}_B \)
12. \( \bs{1}_{A^c \cup B^c} = 1 - \bs{1}_A \bs{1}_B \)
13. \( \bs{1}_{(A \cap B^c) \cup (B \cap A^c)} = \bs{1}_A + \bs{1}_B - 2 \bs{1}_A \bs{1}_B \)
14. \( \bs{1}_{(A \cap B) \cup (A^c \cap B^c)} = 1 - \bs{1}_A - \bs{1}_B + 2 \bs{1}_A \bs{1}_B \)

Припустимо\( A \), що\( B \), і\( C \) є підмножинами універсальної множини\( S \). Дайте індикаторну функцію кожного з наступних, як в терміні\( \bs{1}_A \)\(\bs{1}_B\), так і\( \bs{1}_C \) в сумо-добутовій формі:

1. \( D = \{ x \in S: x \text{ is an element of exactly one of the given sets}\} \)
2. \( E = \{ x \in S: x \text{ is an element of exactly two of the given sets}\} \)

Відповідь

1. \( \bs{1}_D = \bs{1}_A + \bs{1}_B + \bs{1}_C - 2 \left(\bs{1}_A \bs{1}_B + \bs{1}_A \bs{1}_C + \bs{1}_B \bs{1}_C\right) + 3 \bs{1}_A \bs{1}_B \bs{1}_C \)
2. \( \bs{1}_E = \bs{1}_A \bs{1}_B + \bs{1}_A \bs{1}_C + \bs{1}_B \bs{1}_C - 3 \bs{1}_A \bs{1}_B \bs{1}_C \)

Оператори

Нагадаємо стандартні арифметичні оператори на\( \R \) розглянутих вище.

Ми всі знаємо, що сума є комутативною та асоціативною, і цей продукт розподіляється над сумою.

1. Чи є різниця комутативна?
2. Різниця асоціативна?
3. Чи поширюється продукт на різницю?
4. Чи розподіляється сума по продукту?

Відповідь

1. Ні. \( x - y \ne y - x \)
2. Ні. \( x - (y - z) \ne (x - y) - z \)
3. Так. \( x (y - z) = (x y) - (x z) \)
4. Ні. \( x + (y z) \ne (x + y) (x + z) \)

Мультимножини

Висловіть мультимножину\( A \) у формі списку, яка має функцію кратності\( m(a) = 2 \),\( m: \{a, b, c, d, e\} \to \N \) задану\( m(b) = 3 \),\( m(c) = 1 \),\( m(d) = 0 \),\( m(e) = 4 \).

Відповідь

\( A = \{a, a, b, b, b, c, e, e, e, e\} \)

Висловіть прості множники 360 у вигляді множини у вигляді списку.

Відповідь

\(\{2, 2, 2, 3, 3, 5\}\)