1.1: Набори

Last updated
Save as PDF

Page ID: 99256

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

\(\newcommand{\R}{\mathbb{R}}\)\(\newcommand{\N}{\mathbb{N}}\)\(\newcommand{\Z}{\mathbb{Z}}\)\(\newcommand{\Q}{\mathbb{Q}}\)\(\newcommand{\C}{\mathbb{C}}\)\(\newcommand{\A}{\mathbb{A}}\)\(\newcommand{\D}{\mathbb{D}}\)

Теорія множин є основою ймовірності і статистики, як вона є практично для кожної галузі математики.

Множини та підмножини

У цьому тексті множини та їх елементи - примітивні, самоочевидні поняття, підхід, який іноді називають теорією наївних множин.

Набір - це просто сукупність об'єктів; об'єкти називаються елементами множини. Заява, що\(x\) є елементом\(S\) множини\(x \in S\), пишеться, а заперечення, яке не\( x \) є елементом\( S \), пишеться як\( x \notin S \). За визначенням множина повністю визначається її елементами; таким чином множини\(A\) і\(B\) рівні, якщо вони мають однакові елементи:\[ A = B \text{ if and only if } x \in A \iff x \in B \]

Наше наступне визначення - відношення підмножини, ще одне дуже основне поняття.

Якщо\(A\) і\(B\) є множиною, то\(A\) є підмножиною\(B\) якщо кожен елемент також\(A\) є елементом\(B\):\[ A \subseteq B \text{ if and only if } x \in A \implies x \in B \]

Поняття в теорії множин часто ілюструються невеликими схематичними ескізами, відомими як діаграми Венна, названі на честь Джона Венна. Діаграма Венна на малюнку нижче ілюструє відношення підмножини.

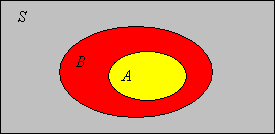
Як зазначалося раніше, членство - це примітивне, невизначене поняття в теорії наївних множин. Однак наступна конструкція, відома як парадокс Рассела, після математика та філософа Бертрана Рассела, показує, що ми не можемо бути занадто кавалером у побудові наборів.

\(R\)Дозволяти бути безліччю всіх наборів\( A \) таких, що\(A \notin A\). Тоді\(R \in R\) якщо і тільки якщо\(R \notin R\).

Доказ

Протиріччя випливає з визначення\( R \): Якщо\( R \in R \), то за визначенням,\( R \notin R \). Якщо\( R \notin R \), то за визначенням,\( R \in R \). Чистий результат, звичайно, полягає в тому, що не\( R \) є чітко визначеним набором.

Зазвичай обговорювані множини в певному контексті - це все підмножини чітко визначеної, заданої множини\(S\), часто званої універсальною множиною. Використання універсального набору запобігає типу проблеми, що виникає в парадоксі Рассела. Тобто, якщо\(S\) є заданою множиною і\(p(x)\) є предикатом на\(S\) (тобто дійсним математичним твердженням, який є істинним або хибним для кожного\(x \in S\)), то\(\{x \in S: p(x)\}\) є дійсним підмножиною\(S\). Визначення множини таким чином відоме як форма предиката. Іншим основним способом визначення набору є просто перерахування його елементів; цей метод відомий як форма списку.

На відміну від універсального набору, порожній набір, що позначається\(\emptyset\), - це набір без елементів.

\(\emptyset \subseteq A\)для кожного набору\(A\).

Доказ

\( \emptyset \subseteq A \)означає, що\( x \in \emptyset \implies x \in A \). Оскільки передумова є помилковою, підтекст істинний.

Один крок вгору від порожнього набору - це набір лише з одним елементом. Такий набір називається однотонним набором. Відношення підмножини є частковим порядком на колекцію підмножин\(S\).

Припустимо\(A\), що,\(B\) і\(C\) є підмножинами множини\(S\). Тоді

\(A \subseteq A\)(Рефлексивне властивість).
Якщо\(A \subseteq B\) і\(B \subseteq A\) тоді\(A = B \) (антисиметрична властивість).
Якщо\(A \subseteq B\) і\(B \subseteq C\) то\(A \subseteq C\) (перехідне властивість).

Ось кілька варіацій щодо відношення підмножини.

Припустимо, що\(A\) і\(B\) є множинами.

Якщо\( A \subseteq B \) і\( A \ne B \), то\( A \) є суворим підмножиною\( B \) і ми іноді пишемо\( A \subset B \).
Якщо\( \emptyset \subset A \subset B \), то\( A \) називається належним підмножиною\( B \).

Збір усіх підмножин заданої множини часто відіграє важливу роль, особливо коли даний множина є універсальною множиною.

Якщо\(S\) є множиною, то множина всіх підмножин\(S\) відома як набір потужності\(S\) і позначається\(\mathscr{P}(S)\).

Спеціальні набори

У цьому тексті використовуються наступні спеціальні набори. Визначення їх також дасть нам практику використання списку та предикатної форми.

Спеціальні набори

\( \R \)позначає множину дійсних чисел і є універсальним набором для інших підмножин в цьому списку.
\(\N = \{0, 1, 2, \ldots\}\)множина натуральних чисел
\(\N_+ = \{1, 2, 3, \ldots\}\)множина натуральних чисел
\(\Z = \{\ldots, -2, -1, 0, 1, 2, \ldots\}\)множина цілих чисел
\(\Q = \{m / n: m \in \Z \text{ and } n \in \N_+ \}\)множина раціональних чисел
\( \A = \{x \in \R: p(x) = 0 \text{ for some polynomial } p \text{ with integer coefficients}\} \)множина алгебраїчних чисел.

Зауважте, що\( \N_+ \subset \N \subset \Z \subset \Q \subset \A \subset \R \). Нам також іноді знадобиться набір комплексних чисел,\(\C = \{x + i y: x, \, y \in \R\}\) де\( i \) є уявна одиниця. Наступні спеціальні раціональні числа виявляються корисними для різних конструкцій.

Бо\( n \in \N \), раціональне число форми,\( j / 2^n \) де\( j \in \Z \) непарне, - це дідічний раціональний (або двійковий раціональний) рангу\( n \).

Бо\( n \in \N \), набір діадичних раціоналів рангу\( n \) або менше є\( \D_n = \{j / 2^n: j \in \Z\} \).
Сукупність всіх діадичних раціональних є\( \D = \{j / 2^n: j \in \Z \text{ and } n \in \N\} \).

Відзначимо, що\( \D_0 = \Z \) і\( \D_n \subset \D_{n+1} \) для\( n \in \N \), і звичайно,\( \D \subset \Q \). Ми використовуємо звичайні позначення для інтервалів дійсних чисел, але знову ж таки визначення надають практику з предикатним позначенням.

Припустимо, що\( a, \, b \in \R \) з\( a \lt b \).

\( [a, b] = \{x \in \R: a \le x \le b\} \). Цей інтервал закритий.
\( (a, b) = \{x \in \R: a \lt x \lt b\} \). Цей інтервал відкритий.
\( [a, b) = \{x \in \R: a \le x \lt b\} \). Цей інтервал закритий-відкритий.
\( (a, b] = \{x \in \R: a \lt x \le b\} \). Цей інтервал є відкрито-закритим.

Терміни відкритий і закритий насправді топологічні поняття.

Ви можете згадати,\( x \in \R \) що раціонально тоді і лише тоді, коли десяткове розширення\( x \) або закінчується, або утворює повторюваний блок. Двійкові раціональні мають прості двійкові розширення (тобто розширення в базовій системі числення 2).

Число\( x \in \R \) є двійковим раціональним рангу\( n \in \N_+ \) тоді і тільки тоді, коли двійкове розширення\( x \) є кінцевим, з\( 1 \) в позиції\( n \) (після роздільника).

Доказ

Досить врахувати\( x \in (0, 1) \). Результат дуже простий, тому ми просто наведемо перші кілька випадків.

Число з рангом 1 -\( 1/2 \) з двійковим розширенням 0,1
Числа з рангом 2 мають\( 1/4 \) розширення 0,01 і\( 3/4 \) з розширенням 0,11
Числа з рангом 3 мають\( 1/8 \) розширення 0.001,\( 3/8 \) з розширенням 0.011,\( 5/8 \) з розширенням 0.101 і\( 7/8 \) з розширенням 0.111.

Встановити операції

Тепер ми готові розглянути основні операції теорії множин. Для наступних визначень припустимо, що\(A\) і\(B\) є підмножинами універсального множини, яким ми будемо позначати\(S\).

Об'єднання\(A\) і\(B\) являє собою набір, отриманий при об'єднанні елементів\(A\) і\(B\). \[ A \cup B = \{x \in S: x \in A \text{ or } x \in B\} \]

Перетин\(A\) і\(B\) являє собою сукупність елементів, загальних для обох\(A\) і\(B\):\[ A \cap B = \{x \in S: x \in A \text{ and } x \in B\}\] Якщо\(A \cap B = \emptyset\) тоді\(A\) і\(B\) нез'єднані.

Так\(A\) і\(B\) є нероз'єднаними, якщо два набори не мають спільних елементів.

Встановлена різниця\(B\) і\(A\) - це набір елементів, які знаходяться в,\(B\) але не в\(A\):\[ B \setminus A = \{x \in S: x \in B \text{ and } x \notin A\} \]

Іноді (особливо в старих роботах і особливо коли\( A \subseteq B \)) замість них\( B - A \) використовується позначення\( B \setminus A \). Коли\( A \subseteq B \),\( B - A \) відомий як правильна встановлена різниця.

Доповненням\(A\) є набір елементів, яких немає в\(A\):\[ A^c = \{ x \in S: x \notin A\} \]

Зауважте, що об'єднання, перетин та різниця є операціями двійкової множини, тоді як доповнення є операцією унарного набору.

У програмі діаграми Венна виберіть кожне з наведених нижче пунктів і зверніть увагу на затінену область на діаграмі.

\(A\)
\(B\)
\(A^c\)
\(B^c\)
\(A \cup B\)
\(A \cap B\)

Основні правила

У наступних теоремах,,\(A\)\(B\), і\(C\) є підмножинами універсальної множини\(S\). Докази прості, і просто використовуйте визначення та основну логіку. Спробуйте самі докази, перш ніж читати ті, що знаходяться в тексті.

\(A \cap B \subseteq A \subseteq A \cup B\).

Закони ідентичності:

\(A \cup \emptyset = A\)
\(A \cap S = A\)

Таким чином, порожня множина діє як ідентичність щодо операції об'єднання, а універсальна множина діє як ідентичність щодо операції перетину.

Ідемпотентні закони:

\(A \cup A = A\)
\(A \cap A = A\)

Доповнюють закони:

\(A \cup A^c = S\)
\(A \cap A^c = \emptyset\)

Закон подвійного доповнення:\((A^c)^c = A\)

Комутативні закони:

\(A \cup B = B \cup A\)
\(A \cap B = B \cap A\)

Доказ

Ці результати випливають з комутативності логічних операторів or та.

Асоціативні закони:

\(A \cup (B \cup C) = (A \cup B) \cup C\)
\(A \cap (B \cap C) = (A \cap B) \cap C\)

Доказ

Ці результати випливають з асоціативності логічних операторів or та.

Таким чином, ми можемо писати\(A \cup B \cup C\) без двозначності. Зауважте, що\( x \) є елементом цієї множини тоді і тільки тоді, коли\( x \) є елементом принаймні одного з трьох заданих множин. Точно так само ми можемо писати\(A \cap B \cap C\) без двозначності. Зауважте, що\( x \) є елементом цієї множини тоді і тільки тоді, коли\( x \) є елементом усіх трьох заданих множин.

Розподільні закони:

\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)

Доказ

\( x \in A \cap (B \cup C) \)якщо і тільки тоді\( x \in A \) і\( x \in B \cup C \) якщо і тільки якщо\( x \in A \) і або\( x \in B \) або\( x \in C \) якщо і тільки тоді\( x \in A \) і\( x \in B\), або, або,\( x \in A \) і\( x \in C \) якщо\( x \in A \cap B \) і тільки\( x \in A \cap C \) якщо і тільки якщо\( x \in (A \cap B) \cup (A \cap C \).
Доказ точно такий же, як і (а), але з або і і поміняний.

Таким чином, перетин розподіляється по об'єднанню, а об'єднання розподіляється по перетину. Цікаво порівняти розподільні властивості теорії множин з властивостями дійсної системи числення. Якщо\(x, \, y, \, z \in \R\), то\(x (y + z) = (x y) + (x z)\), так множення розподіляється над додаванням, але це не так\(x + (y z) = (x + y)(x + z)\), тому додавання не розподіляється над множенням. Наступні результати особливо важливі в теорії ймовірностей.

Закони ДеМоргана (названі на честь Агустуса ДеМоргана):

\((A \cup B)^c = A^c \cap B^c\)
\((A \cap B)^c = A^c \cup B^c\).

Доказ

\( x \in (A \cup B)^c \)якщо і тільки тоді\( x \notin A \cup B \) і тільки якщо\(x \notin A \) і\( x \notin B \) якщо і тільки,\( x \in A^c \) і\( x \in B^c \) якщо і тільки якщо\( x \in A^c \cap B^c \)
\( x \in (A \cap B)^c \)якщо і тільки якщо і тільки\( x \notin A \cap B \) якщо\(x \notin A \) або якщо і тільки або\( x \notin B \) якщо і тільки\( x \in A^c \)\( x \in B^c \) якщо і тільки якщо\( x \in A^c \cup B^c \)

Наступний результат досліджує зв'язки між зв'язком підмножини та операціями набору.

Наступні твердження еквівалентні:

\(A \subseteq B\)
\(B^c \subseteq A^c\)
\(A \cup B = B\)
\(A \cap B = A\)
\(A \setminus B = \emptyset\)

Доказ

Нагадаємо, це\( A \subseteq B \) означає, що\( x \in A \implies x \in B\).
\( B^c \subseteq A^c \)означає, що\( x \notin B \implies x \notin A \). Це контрапозитив (а) і, отже, еквівалентний (а).
Якщо\( A \subseteq B \) то чітко\( A \cup B = B \). І навпаки припустимо\( A \cup B = B \). Якщо\( x \in A \) тоді\( x \in A \cup B \) так\( x \in B \). Звідси\( A \subseteq B \).
Якщо\( A \subseteq B \) то чітко\( A \cap B = A \). І навпаки припустимо\( A \cap B = A \). Якщо\( x \in A \) то\( x \in A \cap B \) і так\( x \in B \). Звідси\( A \subseteq B \).
Припустимо\( A \subseteq B \). Якщо\( x \in A \) тоді\( x \in B \) і так за визначенням,\( x \notin A \setminus B \). Якщо\( x \notin A \) потім знову за визначенням,\( x \notin A \setminus B \). Таким чином\( A \setminus B = \emptyset \). І навпаки, припустимо, що\( A \setminus B = \emptyset \). Якщо\( x \in A \) тоді\( x \notin A \setminus B \) так\( x \in B \). Таким чином\( A \subseteq B \).

На додаток до спеціальних наборів, визначених раніше, у нас також є такі:

Більш спеціальні набори

\( \R \setminus \Q \)це сукупність ірраціональних чисел
\( \R \setminus \A \)це сукупність трансцендентних чисел

З\( \Q \subset \A \subset \R\) цього випливає\( \R \setminus \A \subset \R \setminus \Q \), що кожне трансцендентне число також є ірраціональним.

Встановлена різниця може бути виражена в плані доповнення і перетину. Всі інші множинні операції (доповнення, об'єднання і перетин) можуть бути виражені в терміні різниці.

Результати для різниці набору:

\(B \setminus A = B \cap A^c\)
\(A^c = S \setminus A\)
\(A \cap B = A \setminus (A \setminus B)\)
\(A \cup B = S \setminus \left\{(S \setminus A) \setminus \left[(S \setminus A) \setminus (S \setminus B)\right]\right\}\)

Доказ

Це зрозуміло з визначення:\( B \setminus A = B \cap A^c = \{x \in S: x \in B \text{ and } x \notin A\} \).
Це випливає з (а) с\( B = S \).
Використовуючи (а), закон DeMorgan та розподільний закон, права сторона\[ A \cap (A \cap B^c)^c = A \cap (A^c \cup B) = (A \cap A^c) \cup (A \cap B) = \emptyset \cup (A \cap B) = A \cap B \]
Використовуючи (а), (b), закон DeMorgan та розподільний закон, права сторона\[ \left[A^c \cap (A^c \cap B)^c \right]^c = A \cup (A^c \cap B) = (A \cup A^c) \cap (A \cup B) = S \cap (A \cup B) = A \cup B \]

Таким чином, в принципі, ми могли б зробити все теорії множин, використовуючи одну операцію множини різниці. Але, як припускають (c) і (d), результати були б огидними.

\((A \cup B) \setminus (A \cap B) = (A \setminus B) \cup (B \setminus A)\).

Доказ

Прямий доказ простий, але для практики наведемо доказ, використовуючи множинну алгебру, зокрема закон ДеМоргана, і розподільний закон:\ begin {align} (A\ cup B)\ setminus (A\ cap B) & = (A\ cap B)\ cap (A\ cap B) ^c = (A\ cup B)\ cap (A^c\ b^c)\ & = (A\ cap A^c)\ чашка (B\ cap A^c)\ чашка (A\ cap B ^ c) \ чашка (B\ cap B ^ c)\\ & =\ порожній набір\ чашка (B\ setminus A)\ чашка (A\ setminus B)\ чашка\ порожній набір = (A\ setminus B)\ чашка (B\ setminus A)\ кінець {вирівняти}

Множина в попередньому результаті називається симетричною різницею\(A\) і\(B\), і іноді позначається\(A \bigtriangleup B\). Елементи цієї множини належать до однієї, але не обох заданих множин. Таким чином, симетрична різниця відповідає виключному або таким же чином, що союз відповідає інклюзивному або. Тобто,\( x \in A \cup B \) якщо і тільки якщо\( x \in A \) або\( x \in B \) (або обидва);\( x \in A \bigtriangleup B \) якщо і тільки якщо\( x \in A \) або\( x \in B \), але не обидва. З іншого боку, доповнення симетричної різниці складається з елементів, які належать обом або ні до одного з заданих множин:

\((A \bigtriangleup B)^c = (A \cap B) \cup (A^c \cap B^c) = (A^c \cup B) \cap (B^c \cup A) \)

Доказ

Знову ж таки, прямий доказ простий, але давайте наведемо алгебраїчний доказ для практики:\ begin {вирівнювання} (A\ bigtriangleup B) ^c & =\ left [(A\ cap B)\ cap (A\ cap B) ^c\ cap ^c)\ чашка (A\ cap B)\\ & = (A^c\ чашка A)\ кришка (A^c\ чашка B)\ кришка (B ^ c\ чашка A)\ cap (B ^ c \ чашка B)\\ & = S\ cap (A^c\ чашка B)\ кришка (B ^ c\ чашка A)\ cap S = (A^c\ чашка B)\ кришка (B ^ c\ чашка A)\ кінець {вирівнювання}

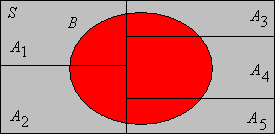
Існує 16 різних (загалом) наборів, які можуть бути побудовані з двох заданих подій\(A\) і\(B\).

Доказ

\( S \)є об'єднанням 4 попарно нероз'єднаних множин:\( A \cap B \)\( A \cap B^c \),,\( A^c \cap B \), і\( A^c \cap B^c \). Якщо\( A \) і\( B \) знаходяться в загальному положенні, ці 4 набори відрізняються. Кожен набір, який може бути побудований з\( A \) і\( B \) є об'єднанням деяких (можливо, жоден, можливо, всі) з цих 4 наборів. Є\( 2^4 = 16 \) підколекції з 4 наборів.

Відкрийте програму діаграми Венна. Ця програма перераховує 16 наборів, які можуть бути побудовані з заданих наборів\( A \) та\( B \) за допомогою встановлених операцій.

Виберіть кожну з чотирьох підмножин у доказі останньої вправи:\( A \cap B \),\( A \cap B^c \),\( A^c \cap B \), і\( A^c \cap B^c \). Зверніть увагу, що це неспільні і їх союз є\( S \).
Виберіть один з інших 12 наборів і покажіть, як кожен є об'єднанням деяких наборів у (a).

Загальні операції

Операції об'єднання та перетину можуть бути легко розширені до скінченної або навіть нескінченної колекції множин.

Визначення

Припустимо, що\(\mathscr{A}\) це непорожня колекція підмножин універсальної множини\(S\). У деяких випадках підмножини в\(\mathscr{A}\) можуть бути природно індексовані непорожнім набором індексів\(I\), так що\(\mathscr{A} = \{A_i: i \in I\}\). (У технічному сенсі будь-яка колекція підмножин може бути проіндексована.)

Об'єднання колекції наборів\(\mathscr{A}\) - це набір, отриманий шляхом об'єднання елементів наборів в\(\mathscr{A}\):\[ \bigcup \mathscr{A} = \{x \in S: x \in A \text{ for some } A \in \mathscr{A}\} \]

Якщо\(\mathscr{A} = \{A_i: i \in I\} \), щоб колекція множин індексувалася, то використовуємо більш природні позначення:\[ \bigcup_{i \in I} A_i =\{x \in S: x \in A_i \text{ for some } i \in I\} \]

Перетином колекції множин\(\mathscr{A}\) є сукупність елементів, загальних для всіх множин в\(\mathscr{A}\):\[ \bigcap \mathscr{A} = \{x \in S: x \in A \text{ for all } A \in \mathscr{A}\} \]

Якщо\(\mathscr{A} = \{A_i : i \in I\}\), щоб колекція множин індексувалася, то використовуємо більш натуральні позначення:\[ \bigcap_{i \in I} A_i = \{x \in S: x \in A_i \text{ for all } i \in I\} \] Часто набір індексів є цілим інтервалом\( \N \). У таких випадках ще більш природним позначенням є використання верхньої і нижньої меж набору індексів. Наприклад, якщо колекція,\( \{A_i: i \in \N_+\} \) то ми б писали\( \bigcup_{i=1}^\infty A_i \) для об'єднання і\( \bigcap_{i=1}^\infty A_i \) для перетину. Аналогічно, якщо колекція\( \{A_i: i \in \{1, 2, \ldots, n\}\} \) для деяких\( n \in \N_+ \), ми б писали\( \bigcup_{i=1}^n A_i \) для союзу і\( \bigcap_{i=1}^n A_i \) для перетину.

\(\mathscr{A}\)Колекція множин попарно нез'єднана, якщо перетин будь-яких двох множин у збірці є порожнім:\(A \cap B = \emptyset\) для кожного\(A, \; B \in \mathscr{A}\) з\(A \ne B\).

\(\mathscr{A}\)Колекція множин, як кажуть, розділяє набір,\(B\) якщо\(\mathscr{A}\) колекція попарно нез'єднана і\(\bigcup \mathscr{A} = B\).

Перегородки тісно пов'язані з відносинами еквівалентності. Як приклад, для\( n \in \N \), множина\[ \mathscr{D}_n = \left\{\left[\frac{j}{2^n}, \frac{j + 1}{2^n}\right): j \in \Z\right\} \] являє собою\( \R \) перегородку на інтервали однакової довжини\(1 / 2^n\). Зверніть увагу, що кінцеві точки є діадичними раціоналами рангу\( n \) або менше, і це\( \mathscr{D}_{n+1} \) можна отримати,\( \mathscr{D}_n \) розділивши кожен інтервал на дві рівні частини. Така послідовність перегородок є однією з причин того, що діадичні раціональні значення мають.

Основні правила

У наступних задачах\(\mathscr{A} = \{A_i : i \in I\}\) є сукупністю підмножин універсальної множини\(S\), індексується непорожньою множиною\(I\), і\(B\) є підмножиною\(S\).

Загальні розподільні закони:

\( \left(\bigcup_{i \in I} A_i \right) \cap B = \bigcup_{i \in I} (A_i \cap B) \)
\( \left(\bigcap_{i \in I} A_i \right) \cup B = \bigcap_{i \in I} (A_i \cup B) \)

Повторюйте закони в позначеннях, де\(\mathscr{A}\) колекція не індексується.

Доказ

\( x \)є елементом множини ліворуч або праворуч від рівняння тоді і тільки якщо\( x \in B \) і\( x \in A_i \) для деяких\( i \in I \).
\( x \)є елементом множини ліворуч або праворуч від рівняння тоді і тільки якщо\( x \in B \) або\( x \in A_i \) для кожного\( i \in I \).

\( \left( \bigcup \mathscr{A} \right) \cap B = \bigcup\{A \cap B: A \in \mathscr{A}\} \),\( \left( \bigcap \mathscr{A} \right) \cup B = \bigcap\{A \cup B: A \in \mathscr{A}\} \)

Загальні закони Де Моргана:

\( \left(\bigcup_{i \in I} A_i \right)^c = \bigcap_{i \in I} A_i^c \)
\( \left(\bigcap_{i \in I} A_i \right)^c = \bigcup_{i \in I} A_i^c \)

Повторюйте закони в позначеннях, де\(\mathscr{A}\) колекція не індексується.

Доказ

\( x \in \left(\bigcup_{i \in I} A_i \right)^c \)якщо і тільки\( x \notin \bigcup_{i \in I} A_i \) якщо і тільки якщо\( x \notin A_i \) для кожного,\( i \in I \) якщо і тільки якщо\( x \in A_i^c \) для кожного,\( i \in I \) якщо і тільки якщо\( x \in \bigcap_{i \in I} A_i^c \).
\( x \in \left(\bigcap_{i \in I} A_i \right)^c \)якщо і тільки\( x \notin \bigcap_{i \in I} A_i \) якщо і тільки якщо\( x \notin A_i \) для деяких,\( i \in I \) якщо і тільки якщо\( x \in A_i^c \) для деяких,\( i \in I \) якщо і тільки якщо\( x \in \bigcup_{i \in I} A_i^c \).

\( \left( \bigcup \mathscr{A} \right)^c = \bigcap\{A^c: A \in \mathscr{A}\}\),\( \left( \bigcap \mathscr{A} \right)^c = \bigcup\{A^c: A \in \mathscr{A}\}\)

Припустимо, що збірка\(\mathscr{A}\) розділів\(S\). Для будь-якої підмножини\(B\),\(\{A \cap B: A \in \mathscr{A}\}\) розділи збірки\(B\).

Доказ

Припустимо\( I \),\( \mathscr{A} = \{A_i: i \in I\} \) де знаходиться набір індексів. Якщо\( i, \, j \in I \) з\( i \ne j \) потім\( (A_i \cap B) \cap (A_j \cap B) = (A_i \cap A_j) \cap B = \emptyset \cap B = \emptyset \), значить, колекція\( \{A_i \cap B: i \in I\} \) розмежовується. Крім того, згідно із законом про розподіл,\[ \bigcup_{i \in I} (A_i \cap B) = \left(\bigcup_{i \in I} A_i\right) \cap B = S \cap B = B \]

Припустимо, що\( \{A_i: i \in \N_+\} \) це сукупність підмножин універсальної множини\( S \)

\( \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k = \left\{x \in S: x \in A_k \text{ for infinitely many } k \in \N_+\right\} \)
\( \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k = \left\{x \in S: x \in A_k \text{ for all but finitely many } k \in \N_+\right\} \)

Доказ

Зверніть увагу, що\( x \in \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k \) якщо і тільки якщо для кожного\( n \in \N_+ \) існує\( k \ge n \) таке, що\( x \in A_k \). У свою чергу, це відбувається якщо і тільки\( x \in A_k \) для нескінченно багатьох\( k \in \N_+ \).
Зверніть увагу, що\( x \in \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k \) якщо і тільки там існує\( n \in \N_+ \) таке, що\( x \in A_k \) для кожного\( k \ge n \). У свою чергу, це відбувається якщо і тільки якщо\( x \in A_k \) для всіх, крім скінченно багатьох\( k \in \N_+ \).

Набори в попередньому результаті виявляються важливими при вивченні ймовірності.

Набори продуктів

Визначення

Набори продуктів - це набори послідовностей. Визначальною властивістю послідовності, звичайно, є те, що порядок, а також членство є важливим.

Почнемо з упорядкованих пар. У цьому випадку визначальним властивістю є те, що\((a, b) = (c, d)\) якщо і тільки якщо\(a = c\) і\(b = d\). Цікаво, що структуру впорядкованої пари можна визначити лише за допомогою теорії множин. Конструкція в результаті нижче зобов'язана Казімєжу Куратовському

Визначте\((a, b) = \{\{a\}, \{a, b\}\}\). Це визначення фіксує визначальну властивість впорядкованої пари.

Доказ

Припустимо, що\( (a, b) = (c, d) \) так\( \{\{a\}, \{a, b\}\} = \{\{c\}, \{c, d\}\} \). У тому випадку, що\( a = b \) зверніть увагу, що\( (a, b) = \{\{a\}\} \). Таким чином ми повинні мати\( \{c\} = \{c, d\} = \{a\} \) і звідси\( c = d = a \), і зокрема,\( a = c \) і\( b = d \). У тому випадку\( a \ne b \), ми повинні мати\( \{c\} = \{a\} \) і, отже,\( c = a \). Але ми не можемо мати,\( \{c, d\} = \{a\} \) тому що тоді\( (c, d) = \{\{a\}\} \) і\( \{a, b\} = \{a\} \), отже, що змусило б\(a = b\), протиріччя. Таким чином, ми повинні мати\( \{c, d\} = \{a, b\} \). Так як\( c = a \) і\( a \ne b \) треба мати\( d = b \). Зворотне тривіальне: якщо\( a = c \) і\( b = d \) то\( \{a\} = \{c\} \) і\( \{a, b\} = \{c, d\} \) так\( (a, b) = (c, d) \).

Звичайно, важливо не переплутати впорядковану пару\( (a, b) \) з відкритим інтервалом\( (a, b) \), так як для обох використовуються однакові позначення. Зазвичай це зрозумілий контекст форми, на який тип об'єкта посилається. Для впорядкованих трійок визначальною властивістю є\( (a, b, c) = (d, e, f) \) якщо і тільки якщо\( a = d \)\( b = e \), і\( c = f \). Впорядковані трійки можуть бути визначені в терміні впорядкованих пар, які за останнім результатом використовують тільки теорію множин.

Визначте\( (a, b, c) = (a, (b, c)) \). Це визначення фіксує визначальну властивість впорядкованої трійки.

Доказ

Припустимо\( (a, b, c) = (d, e, f) \). Потім\( (a, (b, c)) = (d, (e, f)) \). Звідси за визначенням впорядкованої пари ми повинні мати\( a = d \) і\( (b, c) = (e, f) \). Використовуючи визначення знову ми маємо\( b = e \) і\( c = f \). І навпаки, якщо\( a = d \)\( b = e \), і\( c = f \), то\((b, c) = (e, f)\) і значить\( (a, (b, c)) = (d, (e, f)) \). Таким чином\( (a, b, c) = (d, e, f) \).

Все це лише для того, щоб показати, наскільки складні конструкції можуть бути побудовані з більш простих, і в кінцевому підсумку з теорії множин. Але вистачить цього! У загальному випадку дві впорядковані послідовності однакового розміру (скінченна або нескінченна) однакові тоді і лише тоді, коли їх відповідні координати узгоджуються. Таким чином\( n \in \N_+ \), визначення для\( n \) -кортежі є\( (x_1, x_2, \ldots, x_n) = (y_1, y_2, \ldots, y_n) \) якщо і тільки якщо\( x_i = y_i\) для всіх\( i \in \{1, 2, \ldots, n\} \). Для нескінченних послідовностей,\((x_1, x_2, \ldots) = (y_1, y_2, \ldots) \) якщо і тільки якщо\( x_i = y_i \) для всіх\( i \in \N_+ \).

Припустимо, що тепер у нас є послідовність\( n \) множин\((S_1, S_2, \ldots, S_n)\), де\( n \in \N_+ \). Декартове добуток множин визначається наступним чином:\[ S_1 \times S_2 \times \cdots \times S_n = \left\{\left(x_1, x_2, \ldots, x_n\right): x_i \in S_i \text{ for } i \in \{1, 2, \ldots, n\}\right\} \]

Декартові вироби названі на честь Рене Декарта. Якщо\(S_i = S\) для кожного\(i\), то декартові вироби набір можна записати компактно як\(S^n\), декартова сила. Зокрема, нагадаємо, що\(\R\) позначає безліч дійсних чисел так, що\(\R^n\) є\(n\) -мірним евклідовим простором, названим на честь Евкліда, зрозуміло. Елементи\(\{0, 1\}^n\) називаються бітовими рядками довжини\(n\). Як випливає з назви, ми іноді представляємо елементи цього набору продуктів у вигляді рядків, а не послідовностей (тобто опускаємо дужки та коми). Оскільки координати просто приймають два значення, немає ризику плутанини.

Припустимо, що у нас нескінченна послідовність множин\((S_1, S_2, \ldots)\). Декартове добуток множин визначається\[ S_1 \times S_2 \times \cdots = \left\{\left(x_1, x_2, \ldots\right): x_i \in S_i \text{ for each } i \in \{1, 2, \ldots\}\right\} \]

Коли\( S_i = S \) для\( i \in \N_+ \), декартова набір продуктів іноді пишеться як декартова сила як\( S^\infty \) або як\( S^{\N_+} \). Пояснення останнього позначення, а також набагато більш загальна конструкція для виробів множин наведено в наступному розділі, присвяченому функціям. Крім того, позначення, подібне до загального об'єднання та перетину, часто використовується для декартового добутку, з\( \prod \) як оператор. Так\[ \prod_{i=1}^n S_i = S_1 \times S_2 \times \cdots \times S_n, \quad \prod_{i=1}^\infty S_i = S_1 \times S_2 \times \cdots \]

Правила для наборів продуктів

Тепер ми побачимо, як встановлені операції пов'язані з операцією декартового продукту. Припустимо, що\(S\) і\(T\) є множинами і що\(A \subseteq S\),\(B \subseteq S\) і\(C \subseteq T\),\(D \subseteq T\). Множини в теоремах нижче є підмножинами\(S \times T\).

Найважливішими правилами, які пов'язують декартове добуток з об'єднанням, перетином та різницею, є правила розподілу:

Правила розповсюдження товарних наборів

\(A \times (C \cup D) = (A \times C) \cup (A \times D)\)
\((A \cup B) \times C = (A \times C) \cup (B \times C)\)
\(A \times (C \cap D) = (A \times C) \cap (A \times D)\)
\((A \cap B) \times C = (A \times C) \cap (B \times C)\)
\(A \times (C \setminus D) = (A \times C) \setminus (A \times D)\)
\((A \setminus B) \times C = (A \times C) \setminus (B \times C)\)

Доказ

\( (x, y) \in A \times (C \cup D) \)якщо і тільки тоді\( x \in A \) і\( y \in C \cup D \) якщо і тільки якщо\( x \in A \) і або\( y \in C \) або\( y \in D \) якщо і тільки тоді\( x \in A \) і\( y \in C \), або, або,\( x \in A \) і\( y \in D \) якщо\( (x, y) \in A \times C \) і тільки\( (x, y) \in A \times D \) якщо і тільки якщо\( (x, y) \in (A \times C) \cup (A \times D) \).
Подібно до (a), але з ролями координат зворотні.
\( (x, y) \in A \times (C \cap D) \)якщо і тільки тоді\( x \in A \) і\( y \in C \cap D \) якщо і тільки тоді\( x \in A \) і тоді\( y \in C \) і\( y \in D \) якщо і тільки тоді\( (x, y) \in A \times C \) і\( (x, y) \in A \times D \) якщо і тільки тоді\( (x, y) \in (A \times C) \cap (A \times D) \).
Подібно до (c), але з ролями координат зворотні.
\( (x, y) \in A \times (C \setminus D) \)якщо і тільки тоді\( x \in A \) і\( y \in C \setminus D \) якщо і тільки тоді\( x \in A \) і тоді\( y \in C \) і\( y \notin D \) якщо і тільки тоді\( (x, y) \in A \times C \) і\( (x, y) \notin A \times D \) якщо і тільки тоді\( (x, y) \in (A \times C) \setminus (A \times D) \).
Подібно до (e), але з ролями координат зворотні.

В цілому, твір спілок більше, ніж відповідне об'єднання виробів.

\((A \cup B) \times (C \cup D) = (A \times C) \cup (A \times D) \cup (B \times C) \cup (B \times D)\)

Доказ

\( (x, y) \in (A \cup B) \times (C \cup D) \)якщо і тільки тоді\( x \in A \cup B \) і\( y \in C \cup D \) якщо і тільки тоді, коли істинно хоча б одне з наступних:\( x \in A \) і\( y \in C \),\( x \in A \) і\( y \in D \),\( x \in B \) і\( y \in C \),\( x \in B \) і\( y \in D \) якщо і тільки якщо\( (x, y) \in (A \times C) \cup (A \times D) \cup (B \times C) \cup (B \times D) \)

Тому, зокрема, випливає, що\((A \times C) \cup (B \times D) \subseteq (A \cup B) \times (C \cup D)\). З іншого боку, твір перетинів таке ж, як і відповідне перетин виробів.

\((A \times C) \cap (B \times D) = (A \cap B) \times (C \cap D)\)

Доказ

\((x, y) \in (A \times C) \cap (B \times D)\)якщо і тільки тоді\( (x, y) \in A \times C \) і\( (x, y) \in B \times D \) якщо і тільки тоді\( x \in A \) і\( y \in C \) і\( x \in B \) і\( y \in D \) якщо і тільки тоді\( x \in A \cap B \) і\( y \in C \cap D \) якщо і тільки якщо\( (x, y) \in (A \cap B) \times (C \cap D) \).

Загалом, твір відмінностей менше, ніж відповідна різниця продуктів.

\((A \setminus B) \times (C \setminus D) = [(A \times C) \setminus (A \times D)] \setminus [(B \times C) \setminus (B \times D)]\)

Доказ

\( (x, y) \in (A \setminus B) \times (C \setminus D) \)якщо і тільки тоді\( x \in A \setminus B \) і\( y \in C \setminus D \) якщо і тільки якщо\( x \in A \) і\( x \notin B \) і\( y \in C \) і\( y \notin D \). З іншого боку,\( (x, y) \in [(A \times C) \setminus (A \times D)] \setminus [(B \times C) \setminus (B \times D)] \) якщо і тільки якщо\( (x, y) \in (A \times C) \setminus (A \times D) \) і\( (x, y) \notin (B \times C) \setminus (B \times D) \). Перше твердження означає, що\( x \in A \) і\( y \in C \) і\( y \notin D \). Друге твердження - заперечення\( x \in B \) і\( y \in C \) і\( y \notin D \). Обидва твердження тримають, якщо і тільки якщо\( x \in A \) і\( x \notin B \) і\( y \in C \) і\( y \notin D \).

Отже, зокрема випливає\((A \setminus B) \times (C \setminus D) \subseteq (A \times C) \setminus (B \times D)\), що,

Проекції і поперечні перерізи

У цьому обговоренні знову припустимо, що\( S \) і\( T \) є непорожніми множинами, і що\( C \subseteq S \times T \).

Поперечні перерізи

Перетин\( C \) в першій координаті при\( x \in S \) дорівнює\(C_x = \{y \in T: (x, y) \in C\}\)
Перетин\( C \) at у другій координаті при\( y \in T \) дорівнює\[ C^y = \{x \in S: (x, y) \in C\} \]

Зверніть увагу, що\( C_x \subseteq T \) для\( x \in S \) і\( C^y \subseteq S \) для\( y \in T \).

Проекції

Проекція\(C\) на\(T\) є\(C_T = \{y \in T: (x, y) \in C \text{ for some } x \in S\}\).
Проекція\(C\) на\(S\) є\(C^S = \{x \in S: (x, y) \in C \text{ for some } y \in T\}\).

Проекції - це союзи відповідних перетинів.

Профспілки

\( C_T = \bigcup_{x \in S} C_x \)
\( C^S = \bigcup_{y \in T} C^y \)

Поперечні перерізи зберігаються під встановленими операціями. Викладаємо результат для перетинів на\( x \in S \). За симетрії, звичайно, знеболюючі результати тримають за поперечними перерізами при\( y \in T \).

Припустимо, що\( C, \, D \subseteq S \times T \). Тоді для того\( x \in S \),

\( (C \cup D)_x = C_x \cup D_x \)
\( (C \cap D)_x = C_x \cap D_x \)
\( (C \setminus D)_x = C_x \setminus D_x \)

Доказ

\( y \in (C \cup D)_x \)якщо і тільки тоді\( (x, y) \in C \cup D \) і тільки якщо\( (x, y) \in C \) або\( (x, y) \in D \) якщо і тільки якщо\( y \in C_x \) або\( y \in D_x \).
Доказ такий же, як (а), з і заміною або.
Доказ такий же, як (а), з і не замінюючи або.

Для прогнозів результати трохи складніші. Наводимо результати для прогнозів на\( T \); природно, результати для проекцій на\( S \) аналогічні.

Припустимо ще раз, що\( C, \, D \subseteq S \times T \). Тоді

\( (C \cup D)_T = C_T \cup D_T \)
\( (C \cap D)_T \subseteq C_T \cap D_T \)
\( (C_T)^c \subseteq (C^c)_T \)

Доказ

Припустимо, що\( y \in (C \cup D)_T \). Тоді існує\( x \in S \) таке, що\( (x, y) \in C \cup D \). Звідси\( (x, y) \in C \) так\( y \in C_T \), або\( (x, y) \in D \) так\( y \in D_T \). У будь-якому випадку,\( y \in C_T \cup D_T \). І навпаки, припустимо, що\( y \in C_T \cup D_T \). Потім\( y \in C_T \) або\( y \in D_T \). Якщо\( y \in C_T \) тоді існує\( x \in S \) таке, що\( (x, y) \in C \). Але потім\( (x, y) \in C \cup D \) так\( y \in (C \cup D)_T \). Аналогічно, якщо\( y \in D_T \) тоді\( y \in (C \cup D)_T \).
Припустимо, що\( y \in (C \cap D)_T \). Тоді існує\( x \in S \) таке, що\( (x, y) \in C \cap D \). Звідси\( (x, y) \in C \) так\( y \in C_T \) і\( (x, y) \in D \) так\( y \in D_T \). Тому\( y \in C_T \cap D_T \).
Припустимо, що\( y \in (C_T)^c \). Тоді\( y \notin C_T \), так для кожного\( x \in S \),\( (x, y) \notin C \). Виправити\( x_0 \in S \). Тоді\( (x_0, y) \notin C \) так\( (x_0, y) \in C^c \) і тому\( y \in (C^c)_T \).

Легко помітити, що рівність взагалі не тримається частинами (b) і (c). Наприклад, у частині (b) припустимо, що\( A_1, \; A_2 \subseteq S \) вони є непорожніми та\( B \subseteq T \) непорожніми. Нехай\( C = A_1 \times B \) і\( D = A_2 \times B \). Тоді\( C \cap D = \emptyset \) так\( (C \cap D)_T = \emptyset \). Але\( C_T = D_T = B \). Наприклад, у частині (c) припустимо, що\( A \) це непорожня належна підмножина\( S \) і\( B \) є непорожньою власною підмножиною\( T \). Нехай\( C = A \times B \). Тоді\( C_T = B \) так\( (C_T)^c = B^c \). З іншого боку\( C^c = (A^c \times B) \cup (A \times B^c) \cup (A^c \times B^c) \), так\( (C^c)_T = T \).

Поперечні перерізи та проекції будуть розширені до дуже загальних наборів продуктів у наступному розділі, присвяченому Функції.

Обчислювальні вправи

Підмножини\( \R \)

Універсальний набір є\( [0, \infty) \). Нехай\( A = [0, 5] \) і\( B = (3, 7) \). Висловіть кожне з наведених нижче інтервалів:

\( A \cap B \)
\( A \cup B \)
\( A \setminus B \)
\( B \setminus A \)
\( A^c \)

Відповідь

\( (3, 5] \)
\( [0, 7) \)
\( [0, 3] \)
\( (5, 7) \)
\( (5, \infty) \)

Універсальний набір є\( \N \). Нехай\( A = \{n \in \N: n \text{ is even}\} \) і нехай\( B = \{n \in \N: n \le 9\} \). Дайте кожному з наступних дій:

\( A \cap B \)у формі списку
\( A \cup B \)у формі присудка
\( A \setminus B \)у формі списку
\( B \setminus A \)у формі списку
\( A^c \)у формі присудка
\( B^c \)у формі списку

Відповідь

\( \{0, 2, 4, 6, 8\} \)
\( \{n \in \N: n \text{ is even or } n \le 9\} \)
\( \{10, 12, 14, \ldots\} \)
\( \{1, 3, 5, 7, 9\} \)
\( \{n \in \N: n \text{ is odd}\} \)
\( \{10, 11, 12, \ldots\} \)

Монети та кубики

Нехай\(S = \{1, 2, 3, 4\} \times \{1, 2, 3, 4, 5, 6\}\). Це набір результатів, коли 4-стороння матриця та 6-стороння матриця кидаються. Далі нехай\(A = \{(x, y) \in S: x = 2\}\) і\(B = \{(x, y) \in S: x + y = 7\}\). Надайте кожному з наступних наборів у вигляді списку:

\(A\)
\(B\)
\(A \cap B\)
\(A \cup B\)
\(A \setminus B\)
\(B \setminus A\)

Відповідь

\(\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)\}\)
\(\{(1, 6), (2, 5), (3, 4), (4, 3)\}\)
\(\{(2, 5)\}\)
\(\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (1, 6), (3, 4), (4, 3)\}\)
\(\{(2, 1), (2, 2), (2, 3), (2, 4), (2, 6)\}\)
\(\{(1, 6), (3, 4), (4, 3)\}\)

Нехай\(S = \{0, 1\}^3\). Це набір результатів, коли монета кидається 3 рази (0 позначає хвости, а 1 позначає голови). Далі нехай\(A = \{(x_1, x_2, x_3) \in S: x_2 = 1\}\) і\(B = \{(x_1, x_2, x_3) \in S: x_1 + x_2 + x_3 = 2\}\). Дайте кожному з наступних наборів у вигляді списку, використовуючи позначення bit-string:

\(S\)
\(A\)
\(B\)
\(A^c\)
\(B^c\)
\(A \cap B\)
\(A \cup B\)
\(A \setminus B\)
\(B \setminus A\)

Відповідь

\(\{000, 100, 010, 001, 110, 101, 011, 111\}\)
\(\{010, 110, 011, 111\}\)
\(\{110, 011, 101\}\)
\(\{000, 100, 001, 101\}\)
\(\{000, 100, 010, 001, 111\}\)
\(\{110, 011\}\)
\(\{010, 110, 011, 111, 101\}\)
\(\{010, 111\}\)
\(\{101\}\)

Нехай\(S = \{0, 1\}^2\). Це набір результатів, коли монета кидається двічі (0 позначає хвости, а 1 позначає голови). Дайте\(\mathscr{P}(S)\) у вигляді списку.

Відповідь

\(\{\emptyset, \{00\}, \{01\}, \{10\}, \{11\}, \{00, 01\}, \{00, 10\}, \{00, 11\}, \{01, 10\}, \{01, 11\}, \{10, 11\}, \{00, 01, 10\}, \{00, 01, 11\}, \{00, 10, 11\}, \{01, 10, 11\}, \{00, 01, 10, 11\}\}\)

Картки

Стандартна колода карт може бути змодельована декартовим набором продуктів,\[ D = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, j, q, k\} \times \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\} \] де перша координата кодує номінал або вид (туз, 2—10, валет, дама, король) і де друга координата кодує масть (трефи, алмази, серця, піки). Іноді ми представляємо карту як рядок, а не впорядковану пару (наприклад,\(q \heartsuit\) для королеви сердець). Для завдань в цьому підрозділі карткова колода\(D\) є універсальним набором.

Нехай\(H\) позначають набір сердець і набір\(F\) лицьових карт. Знайдіть кожне з наведених нижче варіантів:

\(H \cap F\)
\(H \setminus F\)
\(F \setminus H\)
\(H \bigtriangleup F\)

Відповідь

\(\{j \heartsuit, q \heartsuit, k \heartsuit\}\)
\(\{1 \heartsuit, 2 \heartsuit, 3 \heartsuit, 4 \heartsuit, 5 \heartsuit, 6 \heartsuit, 7 \heartsuit, 8 \heartsuit, 9 \heartsuit, 10 \heartsuit\}\)
\(\{j \spadesuit, q \spadesuit, k \spadesuit, j \diamondsuit, q \diamondsuit, k \diamondsuit, j \clubsuit, q \clubsuit, k \clubsuit\}\)
\(\{1 \heartsuit, 2 \heartsuit, 3 \heartsuit, 4 \heartsuit, 5 \heartsuit, 6 \heartsuit, 7 \heartsuit, 8 \heartsuit, 9 \heartsuit, 10 \heartsuit, j \spadesuit, q \spadesuit, k \spadesuit, j \diamondsuit, q \diamondsuit, k \diamondsuit, j \clubsuit, q \clubsuit, k \clubsuit\}\)

Рука моста - це підмножина\( D \) з 13 картами. Часто мостовидні руки описуються шляхом надання перетинів по масті.

Припустимо, що\( N \) це рука моста, яку утримує гравець на ім'я Північ, визначена\[ N^\clubsuit = \{2, 5, q\}, \, N^\diamondsuit = \{1, 5, 8, q, k\}, \, N^\heartsuit = \{8, 10, j, q\}, \, N^\spadesuit = \{1\} \] знаком кожного з наступних дій:

Непорожні перерізи\( N \) за номіналом.
Проекція\( N \) на набір костюмів.
Проекція\( N \) на безліч номіналів

Відповідь

\( N_1 = \{\diamondsuit, \spadesuit\} \),\( N_2 = \{\clubsuit\} \),\( N_5 = \{\clubsuit, \diamondsuit\} \),\( N_8 = \{\diamondsuit, \heartsuit\} \),\( N_{10} = \{\heartsuit\} \),\( N_j = \{\heartsuit\} \),\( N_q = \{\clubsuit, \diamondsuit, \heartsuit\} \),\( N_k = \{\diamondsuit\} \)
\( \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\} \)
\( \{1, 2, 5, 8, 10, j, q, k\} \)

На відміну від цього, зазвичай корисніше описати покер руку, даючи поперечні перерізи за номіналом. У звичайному варіанті розіграшу покеру рука - це підмножина\( D \) з 5 картами.

Припустимо, що\( B \) це покерна рука, яку проводить гравець на ім'я Білл, з\[ B_1 = \{\clubsuit, \spadesuit\}, \, B_8 = \{\clubsuit, \spadesuit\}, \, B_q = \{\heartsuit\} \] Знайти кожну з наступних дій:

Непорожні перерізи\( B \) по масті.
Проекція\( B \) на набір костюмів.
Проекція\( B \) на безліч номіналів

Відповідь

\( B^\clubsuit = \{1, 8\} \),\( B^\heartsuit = \{q\} \),\( B^\spadesuit = \{1, 8\} \)
\( \{\clubsuit, \heartsuit, \spadesuit\} \)
\( \{1, 8, q\} \)

Рука покеру в останній вправі відома як рука мертвої людини. Легенда свідчить, що Дикий Білл Хікок тримав цю руку під час свого вбивства в 1876 році.

Загальні спілки і перехрестя

Для проблем в цьому підрозділі універсальний набір є\(\R\).

Нехай\(A_n = [0, 1 - \frac{1}{n}]\) для\(n \in \N_+\). Знайти

\(\bigcap_{n=1}^\infty A_n\)
\(\bigcup_{n=1}^\infty A_n\)
\(\bigcap_{n=1}^\infty A_n^c\)
\(\bigcup_{n=1}^\infty A_n^c\)

Відповідь

\(\{0\}\)
\([0, 1)\)
\((-\infty, 0) \cup [1, \infty)\)
\(\R - \{0\}\)

Нехай\(A_n = (2 - \frac{1}{n}, 5 + \frac{1}{n})\) для\(n \in \N_+\). Знайти

\(\bigcap_{n=1}^\infty A_n\)
\(\bigcup_{n=1}^\infty A_n\)
\(\bigcap_{n=1}^\infty A_n^c\)
\(\bigcup_{n=1}^\infty A_n^c\)

Відповідь

\([2, 5]\)
\((1, 6)\)
\((-\infty, 1] \cup [6, \infty)\)
\((-\infty, 2) \cup (5, \infty)\)

Підмножини\( \R^2 \)

\( T \)Дозволяти бути замкнутий трикутної області в\( \R^2 \) з вершинами\( (0, 0) \)\( (1, 0) \),, і\( (1, 1) \). Знайдіть кожне з наведених нижче варіантів:

Перетин\( T_x \) для\( x \in \R \)
Перетин\( T^y \) для\( y \in \R \)
Проекція\( T \) на горизонтальну вісь
Проекція\( T \) на вертикальну вісь

Відповідь

\( T_x = [0, x] \)для\( x \in [0, 1] \),\( T_x = \emptyset \) інакше
\( T^y = [y, 1] \)для\( y \in [0, 1] \),\( T^y = \emptyset \) інакше
\( [0, 1] \)
\( [0, 1] \)