Skip to main content
LibreTexts - Ukrayinska

5.7: Глава Практика

  1. Last updated
  2. Save as PDF
  • Page ID
    99959

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    5.1 Властивості неперервних функцій щільності ймовірностей

    1.

    Який тип розподілу ілюструє графік?

    Горизонтальна вісь коливається від 0 до 10. Розподіл моделюється прямокутником, що простягається від x = 3 до x =8.

    Малюнок\(\PageIndex{23}\)

    2.

    Який тип розподілу ілюструє графік?

    Цей графік нахиляється вниз. Він починається в точці на осі y і наближається до осі x біля правого краю графіка.

    Малюнок\(\PageIndex{24}\)

    3.

    Який тип розподілу ілюструє графік?

    На цьому графіку зображений дзвоноподібний графік. Симетричний графік досягає максимальної висоти при x = 0 і нахиляється вниз поступово до осі x з кожного боку піку.

    Малюнок\(\PageIndex{25}\)

    4.

    Що являє собою затінена область? \(P\)(___\(< x <\) ___)

    Цей графік показує рівномірний розподіл. Горизонтальна вісь коливається від 0 до 10. Розподіл моделюється прямокутником, що простягається від x = 1 до x = 8. Область від x = 2 до x = 5 затінюється всередині прямокутника.

    Малюнок\(\PageIndex{26}\)

    5.

    Що являє собою затінена область? \(P\)(___\(< x <\) ___)

    Цей графік показує експоненціальний розподіл. Графік нахиляється вниз. Він починається в точці на осі y і наближається до осі x біля правого краю графіка. Область під графом від х = 6 до х = 7 затінюється.

    Малюнок\(\PageIndex{27}\)

    6.

    Для безперервного розподілу ймовірностей,\(0 \leq x \leq 15\). Що таке\(P(x > 15)\)?

    7.

    Що таке площа під,\(f(x)\) якщо функція є безперервною функцією щільності ймовірності?

    8.

    Для безперервного розподілу ймовірностей,\(0 \leq x \leq 10\). Що таке\(P(x = 7)\)?

    9.

    Безперервна функція ймовірності обмежена частиною між\(x = 0\) і\(7\). Що таке\(P(x = 10)\)?

    10.

    \(f(x)\)для безперервної функції ймовірності є\(\frac{1}{5}\), а функція обмежена\(0 \leq x \leq 5\). Що таке\(P(x < 0)\)?

    11.

    \(f(x)\), безперервна функція ймовірності\(\frac{1}{12}\), дорівнює, і функція обмежена\(0 \leq x \leq 12\). Що таке\(P(0 < x < 12)\)?

    12.

    Знайдіть ймовірність того, що\(x\) потрапляє в затінену область.

    Малюнок\(\PageIndex{28}\)

    13.

    Знайдіть ймовірність того, що\(x\) потрапляє в затінену область.

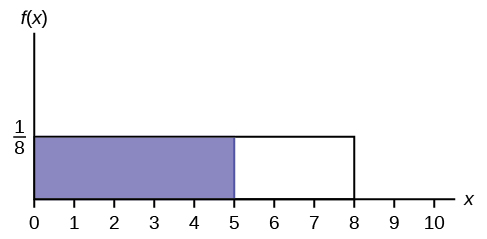    902063719447 ед 776б 3c000cae 81 х 74 д 9 с2 ф 5 (1) .jpg
    Малюнок\(\PageIndex{29}\)

    14.

    Знайдіть ймовірність того, що\(x\) потрапляє в затінену область.

    Малюнок\(\PageIndex{30}\)

    15.

    \(f(x)\), безперервна функція ймовірності, дорівнює\(\frac{1}{3}\) і функція обмежена\(1 \leq x \leq 4\). Опишіть\(P(x>\frac{3}{2})\).

    5.2 Рівномірний розподіл

    Використовуйте наступну інформацію, щоб відповісти на наступні десять питань. Дані, які слідують, - це квадратні метри (у квадраті 1000 футів) 28 будинків.

    \ (\ індекс сторінки {2}\) «>
    1.5 2.4 3.6 2.6 1.6 2.4 2.0
    3.5 2.5 1.8 2.4 2.5 3.5 4.0
    2.6 1.6 2.2 1.8 3.8 2.5 1.5
    2.8 1.8 4.5 1.9 1.9 3.1 1.6
    Таблиця\(\PageIndex{2}\)

    Середнє значення зразка = 2,50 і стандартне відхилення зразка = 0,8302.

    Дистрибутив можна записати як\(X \sim U(1.5, 4.5)\).

    16.

    Що це за тип дистрибуції?

    17.

    У цьому розподілі результати однаково вірогідні. Що це означає?

    18.

    Яка висота\(f(x)\) для безперервного розподілу ймовірностей?

    19.

    Які обмеження для значень\(x\)?

    20.

    Графік\(P(2 < x < 3)\).

    21.

    Що таке\(P(2 < x < 3)\)?

    22.

    Що таке\(P(x < 3.5 | x < 4)\)?

    23.

    Що таке\(P(x = 1.5)\)?

    24.

    Знайдіть ймовірність того, що випадково обраний будинок має більше 3,000 квадратних футів, враховуючи, що ви вже знаєте, що будинок має більше 2,000 квадратних футів.

    Використовуйте наступну інформацію, щоб відповісти на наступні вісім вправ. Розподіл дається як\(X \sim U(0, 12)\).

    25.

    Що таке\(a\)? Що вона собою являє?

    26.

    Що таке\(b\)? Що вона собою являє?

    27.

    Що таке функція щільності ймовірності?

    28.

    Що таке теоретичне означає?

    29.

    Що таке теоретичне стандартне відхилення?

    30.

    Намалюйте графік розподілу для\(P(x > 9)\).

    31.

    Знайти\(P(x > 9)\).

    Використовуйте наступну інформацію, щоб відповісти на наступні одинадцять вправ. Вік автомобілів на стоянці персоналу заміського коледжу рівномірно розподіляється від півроку (0,5 року) до 9,5 років.

    32.

    Що тут вимірюється?

    33.

    У словах визначаємо випадкову величину\(X\).

    34.

    Дані дискретні або безперервні?

    35.

    Інтервал значень для\(x\) - ______.

    36.

    Розподіл\(X\) для ______.

    37.

    Запишіть функцію щільності ймовірності.

    38.

    Графік розподілу ймовірностей.

    1. Намалюйте графік розподілу ймовірностей.
      Це порожній шаблон графіка. Вертикальні та горизонтальні осі не мають маркування.

      Малюнок\(\PageIndex{31}\)

    2. Визначте наступні значення:
      • Найнижче значення для\(\overline{x}\): _______
      • Найвище значення для\(\overline{x}\): _______
      • Висота прямокутника: _______
      • Мітка для осі x (слова): _______
      • Мітка для осі y (слова): _______

    39.

    Знайдіть середній вік автомобілів в партії.

    40.

    Знайдіть ймовірність того, що випадково обраному автомобілю в партії було менше чотирьох років.

    1. Намалюйте графік і затіньте цікаву область.
      Пустий графік з вертикальною та горизонтальною осями.

      Малюнок\(\PageIndex{32}\)

    2. Знайдіть ймовірність. \(P(x < 4)\)= _______

    41.

    Розглядаючи тільки автомобілі менше 7,5 років, знайдіть ймовірність того, що випадково обраному автомобілю в партії було менше чотирьох років.

    1. Намалюйте графік, затіньте цікаву область.
      Це порожній шаблон графіка. Вертикальні та горизонтальні осі не мають маркування.

      Малюнок\(\PageIndex{33}\)

    2. Знайдіть ймовірність. \(P(x < 4 | x < 7.5) =\)_______

    42.

    Що змінилося в попередніх двох проблемах, які зробили рішення різними?

    43.

    Знайдіть третій квартиль вікових автомобілів в партії. Це означає, що вам доведеться знайти значення таке\(\frac{3}{4}\), що або 75% автомобілів є максимум (менше або дорівнює) цього віку.

    1. Намалюйте графік і затіньте цікаву область.
      Пустий графік з вертикальною та горизонтальною осями.

      Малюнок\(\PageIndex{34}\)

    2. Знайдіть значення\(k\) таке, що\(P(x < k) = 0.75\).
    3. Третій квартиль - _______

    5.3 Експоненціальний розподіл

    Використовуйте наступну інформацію, щоб відповісти на наступні десять вправ. Представник служби підтримки клієнтів повинен витрачати різну кількість часу з кожним клієнтом для вирішення різних проблем. Кількість часу, витраченого з кожним замовником, можна змоделювати наступним розподілом:\(X \sim Exp(0.2)\)

    44.

    Що це за тип дистрибуції?

    45.

    Чи однаково ймовірні результати в цьому розподілі? Чому чи чому ні?

    46.

    Що таке\(m\)? Що вона собою являє?

    47.

    Що таке середнє?

    48.

    Що таке стандартне відхилення?

    49.

    Створити функцію щільності ймовірності.

    50.

    Графік розподілу.

    51.

    Знайти\(P(2 < x < 10)\).

    52.

    Знайти\(P(x > 6)\).

    53.

    Знайдіть 70-й процентиль.

    Використовуйте наступну інформацію, щоб відповісти на наступні сім вправ. Розподіл дається як\(X \sim Exp(0.75)\).

    54.

    Що таке м?

    55.

    Що таке функція щільності ймовірності?

    56.

    Що таке функція кумулятивного розподілу?

    57.

    Намалюйте розподіл.

    58.

    Знайти\(P(x < 4)\).

    59.

    Знайдіть 30-й процентиль.

    60.

    Знайдіть медіану.

    61.

    Що більше, середнє або медіана?

    Використовуйте наступну інформацію, щоб відповісти на наступні 16 вправ. Вуглець-14 - радіоактивний елемент з періодом напіврозпаду близько 5730 років. Вуглець-14, як кажуть, розпадається експоненціально. Швидкість розпаду становить 0,000121. Починаємо з одного грама вуглецю-14. Нас цікавить час (роки), необхідний для розпаду вуглецю-14.

    62.

    Що тут вимірюється?

    63.

    Дані дискретні або безперервні?

    64.

    У словах визначаємо випадкову величину\(X\).

    65.

    Що таке швидкість розпаду (\(m\))?

    66.

    Розподіл\(X\) для ______.

    67.

    Знайдіть кількість (відсоток одного грама) вуглецю-14 тривалістю менше 5730 років. Це означає, знайдіть\(P(x < 5,730)\).

    1. Намалюйте графік і затіньте цікаву область.
      Це порожній шаблон графіка. Вертикальні та горизонтальні осі не мають маркування.

      Малюнок\(\PageIndex{35}\)

    2. Знайдіть ймовірність. \(P(x < 5,730) =\)__________

    68.

    Знайдіть відсоток вуглецю-14 тривалістю більше 10 000 років.

    1. Намалюйте графік і затіньте цікаву область.
      Пустий графік з горизонтальною і вертикальною осями.

      Малюнок\(\PageIndex{36}\)

    2. Знайдіть ймовірність. \(P(x > 10,000) =\)________

    69.

    Тридцять відсотків (30%) вуглецю-14 розпадуться протягом скількох років?

    1. Намалюйте графік і затіньте цікаву область.
      Це порожній шаблон графіка. Вертикальні та горизонтальні осі не мають маркування.

      Малюнок\(\PageIndex{37}\)

      Знайдіть значення\(k\) таке, що\(P(x < k) = 0.30\).